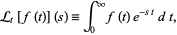SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Je kunt dit rechtstreeks herleiden uit de definitie van de Laplacetransformatie:quote:Op vrijdag 26 maart 2010 13:06 schreef GoodGawd het volgende:
Ik heb hier in een som staan:
Laplace(f(5t)) = 1/5 F (s/5)
Waarom is dat zo? Kan je dat herleiden aan de hand van een rekenregel?
Zij ℒ[f(t)](s) = F(s). Om nu aan de hand van de definitie ℒ[f(5t)](s) te bepalen voer je een integraalsubstitutie t = τ/5 (en dus dt = dτ/5) uit, en dan zie je direct dat ℒ[f(5t)](s) = 1/5∙F(s/5).


Is dat convolutie product gebeuren moeilijk of ligt dat aan mij?
Blues ain't nothing but a good man feeling bad...


Hallo, weet iemand hier op je op een casio fx-9850gb de standaardafwijking kunt bepalen als je de gemiddelde en de opp hebt (bij een normale verdeling)?


De oppervlakte is altijd 1, dus dat zegt niet zoveel.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Ja maar niet als er een oppervlakje uitgesneden is met 1 (en dan verder tot zo ver mogelijk links, of rechts) of 2 verticale strepen, waar een getal bij staatquote:Op vrijdag 26 maart 2010 19:55 schreef GlowMouse het volgende:
De oppervlakte is altijd 1, dus dat zegt niet zoveel.


sorry,Ik bedoelde P3quote:Op donderdag 25 maart 2010 21:19 schreef Hanneke12345 het volgende:
[..]
Mja, op deze manier hoor je wel coördinaten op te tellen voor zover ik weet.
Het gaat nergens om P4, toch?
pff, kutvak. ;x


Een vraagje:
Zij X < Am en Y < An twee affiene irreducibele gesloten verzamelingen. Dan geldt dim XxY <= dim X + dim Y waarbij XxY < Am+n de geinduceerde Zariski topologie krijgt.
Ik heb hopeloos dit proberen te bewijzen. Blijkbaar moet ik nog veel weten over commutatieve algebra. Ik gebruik T voor het tensorsymbool. Dan is er een k-algebra isomorfisme van de coordinatenring A(XxY) naar A(X)TA(Y). Deze wil ik gebruiken samen met het feit dat dim X= dim A(X), dim Y= dim A(Y) of met een stelling over de transcendental-degree die ook iets zegt over de dimensie. Ik ben benieuwd hoe priemidealen in A(X)TA(Y) eruit zien...misschien kom ik dan wel uit!
Heeft iemand een idee?
Zij X < Am en Y < An twee affiene irreducibele gesloten verzamelingen. Dan geldt dim XxY <= dim X + dim Y waarbij XxY < Am+n de geinduceerde Zariski topologie krijgt.
Ik heb hopeloos dit proberen te bewijzen. Blijkbaar moet ik nog veel weten over commutatieve algebra. Ik gebruik T voor het tensorsymbool. Dan is er een k-algebra isomorfisme van de coordinatenring A(XxY) naar A(X)TA(Y). Deze wil ik gebruiken samen met het feit dat dim X= dim A(X), dim Y= dim A(Y) of met een stelling over de transcendental-degree die ook iets zegt over de dimensie. Ik ben benieuwd hoe priemidealen in A(X)TA(Y) eruit zien...misschien kom ik dan wel uit!
Heeft iemand een idee?


Ik probeer de volgende stelling te bewijzen:
Stelling: Als A=A* (A* is de getransponeerde complex geconjugeerde van A), dan A>0 (A is "positive definite") desda alle eigenwaarden van A positief zijn.
Bewijs:
Stel alle eigenwaarden zijn positief. Omdat A=A* is A orthogonaal te diagonaliseren. Er bestaat dus een unitaire matrix U zo dat A=UDU* met D=diag(L1,...,Ln) met Lk positieve eigenwaarden voor alle k.
en nu?
Stelling: Als A=A* (A* is de getransponeerde complex geconjugeerde van A), dan A>0 (A is "positive definite") desda alle eigenwaarden van A positief zijn.
Bewijs:
Stel alle eigenwaarden zijn positief. Omdat A=A* is A orthogonaal te diagonaliseren. Er bestaat dus een unitaire matrix U zo dat A=UDU* met D=diag(L1,...,Ln) met Lk positieve eigenwaarden voor alle k.
en nu?


Moet je dat niet juist bewijzen?quote:Op zondag 28 maart 2010 12:07 schreef BasementDweller het volgende:
Bewijs:
Stel alle eigenwaarden zijn positief. Omdat A=A* is A orthogonaal te diagonaliseren. Er bestaat dus een unitaire matrix U zo dat A=UDU* met D=diag(L1,...,Ln) met Lk positieve eigenwaarden voor alle k.
A>0 => alle ew. positief kun je uit het ongerijmde bewijzen
alle ew. positief => A>0 kun je bewijzen door gebruik te maken dat de eigenvectoren R^n opspannen.
[ Bericht 0% gewijzigd door GlowMouse op 28-03-2010 17:12:33 ]
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Stel A = A* > 0 en niet alle e.w. zijn positief. Dan bestaat er een Lk=<0. Voor de bijbehorende eigenvector vk geldt: Mvk= Lk vk. Aan beide kanten het inproduct nemen met vk* geeft: (M vk,vk)=Lk(vk,vk). Omdat het inproduct van een vector ongelijk aan nul met zichzelf groter of gelijk is aan nul en Lk niet-positief is, volgt: (M vk,vk)=<0), tegenspraak.
Nu de andere kant nog.
Nu de andere kant nog.


De andere kant op:
Stel A>0. Omdat A=A*, bestaat er een orthonormaal stelsel van eigenvectoren en dus een unitaire matrix U zdd D=U*AU=diag(L1,..,Ln). Dus A=UDU*. Uit A>0 volgt UDU*>0.
Kan ik hier iets mee?
(en was mijn eerste bewijs goed?)
Stel A>0. Omdat A=A*, bestaat er een orthonormaal stelsel van eigenvectoren en dus een unitaire matrix U zdd D=U*AU=diag(L1,..,Ln). Dus A=UDU*. Uit A>0 volgt UDU*>0.
Kan ik hier iets mee?
(en was mijn eerste bewijs goed?)


"de bijbehorende eigenvector" bestaat niet.
En nee, probeer de hint tegebruiken
En nee, probeer de hint tegebruiken
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Met de bijbehorende eigenvector bedoel ik de eigenvector die bij die eigenwaarde hoort. Bestaat deze niet volgens jou?quote:Op zondag 28 maart 2010 15:41 schreef GlowMouse het volgende:
"de bijbehorende eigenvector" bestaat niet.
En nee, probeer de hint tegebruiken
En die hint, dat de eigenvectoren R^n opspannen heb ik gebruikt (want omdat ze R^n opspannen bestaat er een unitaire matrix U). Ik zou niet weten hoe ik het anders kan gebruiken... (we werken trouwens niet alleen in R^n maar ook in C^n)


Ik zou gebruiken dat de dimensie gelijk is aan de transcendentiegraad van het functielichaam.quote:Op zaterdag 27 maart 2010 18:25 schreef Optimistic1 het volgende:
Een vraagje:
Zij X < Am en Y < An twee affiene irreducibele gesloten verzamelingen. Dan geldt dim XxY <= dim X + dim Y waarbij XxY < Am+n de geinduceerde Zariski topologie krijgt.
Ik heb hopeloos dit proberen te bewijzen. Blijkbaar moet ik nog veel weten over commutatieve algebra. Ik gebruik T voor het tensorsymbool. Dan is er een k-algebra isomorfisme van de coordinatenring A(XxY) naar A(X)TA(Y). Deze wil ik gebruiken samen met het feit dat dim X= dim A(X), dim Y= dim A(Y) of met een stelling over de transcendental-degree die ook iets zegt over de dimensie. Ik ben benieuwd hoe priemidealen in A(X)TA(Y) eruit zien...misschien kom ik dan wel uit!
Heeft iemand een idee?


Het idee is dat je bij <Ax,x> x schrijft als lineaire combinatie van eigenvectoren. Maar ik vraag me even af of je niet nodig hebt dat A reëel is (anders weet ik niet of de eigenwaarden en -vectoren reëel zijn).quote:Op zondag 28 maart 2010 15:44 schreef BasementDweller het volgende:
[..]
Met de bijbehorende eigenvector bedoel ik de eigenvector die bij die eigenwaarde hoort. Bestaat deze niet volgens jou?
En die hint, dat de eigenvectoren R^n opspannen heb ik gebruikt (want omdat ze R^n opspannen bestaat er een unitaire matrix U). Ik zou niet weten hoe ik het anders kan gebruiken... (we werken trouwens niet alleen in R^n maar ook in C^n)
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Als je wil aantonen dat een verzameling gesloten is, kan je laten zien dat de verzameling gelijk is aan zijn afsluiting. Als je echter wil aantonen dat een verzameling gesloten is in een andere verzameling, wat moet je dan precies laten zien?


Mijn vragen: Stel je hebt een empirical cumulative distribution function en hier moet je een histogram van maken.
- Hoe benader je deze functie met een andere functie zodat als je de afgeleide van deze functie neemt je de bucket sizes en bucket boundaries krijgt?
- Hoe benader je deze functie met een andere functie zodat als je de afgeleide van deze functie neemt je de optimale bucket sizes en bucket boundaries krijgt?
Ik ben erachter dat je een ecdf kan benaderen met een cdf en dan ook een bijbehorende pdf hebt. Er wordt gehint naar lineaire functies omdat het differentieren van lineaire functies getallen opleveren die volgens mij het antwoord op de vraag zijn. De ecdf benaderen met een lineaire functie lijkt me onverantwoord. De enige andere lineaire functies die ik hier tevoorschijn kan toveren zijn de raaklijnen van de cdf en pdf.
Ik heb een manier gevonden om op een arbitrair punt de hoogte en breedte van een bucket te vinden. Er is ook gehint naar de mate van optimaliteit gelijk stellen aan de goodness of fit van de cdf op de ecdf alleen zie ik totaal niet hoe ik hier optimale bucket boundaries af kan leiden. Ik hoop zeer dat ik duidelijk ben en dat iemand me op weg kan helpen.
- Hoe benader je deze functie met een andere functie zodat als je de afgeleide van deze functie neemt je de bucket sizes en bucket boundaries krijgt?
- Hoe benader je deze functie met een andere functie zodat als je de afgeleide van deze functie neemt je de optimale bucket sizes en bucket boundaries krijgt?
Ik ben erachter dat je een ecdf kan benaderen met een cdf en dan ook een bijbehorende pdf hebt. Er wordt gehint naar lineaire functies omdat het differentieren van lineaire functies getallen opleveren die volgens mij het antwoord op de vraag zijn. De ecdf benaderen met een lineaire functie lijkt me onverantwoord. De enige andere lineaire functies die ik hier tevoorschijn kan toveren zijn de raaklijnen van de cdf en pdf.
Ik heb een manier gevonden om op een arbitrair punt de hoogte en breedte van een bucket te vinden. Er is ook gehint naar de mate van optimaliteit gelijk stellen aan de goodness of fit van de cdf op de ecdf alleen zie ik totaal niet hoe ik hier optimale bucket boundaries af kan leiden. Ik hoop zeer dat ik duidelijk ben en dat iemand me op weg kan helpen.
<tsjsieb> maarja, jij bent ook gewoon cool R-Mon :p


A is gesloten in S als A gelijk is aan de afsluiting van A doorsneden met S.quote:Op maandag 29 maart 2010 23:46 schreef BasementDweller het volgende:
Als je wil aantonen dat een verzameling gesloten is, kan je laten zien dat de verzameling gelijk is aan zijn afsluiting. Als je echter wil aantonen dat een verzameling gesloten is in een andere verzameling, wat moet je dan precies laten zien?


Bedankt!quote:Op dinsdag 30 maart 2010 17:19 schreef thabit het volgende:
[..]
A is gesloten in S als A gelijk is aan de afsluiting van A doorsneden met S.


Hey ik heb ook een vraagje
Ik heb zeg maar een data set met 6 attributes die allemaal numeriek zijn.
Het idee is dat je 5 coefficienten vindt die de dataset zeg maar goed fitten. Die heb ik dus gevonden, nou heb ik alleen een ander probleem waarmee ik zit. Het gaat over de sufficient/necessary number of instances die je nodig moet hebben om aan je beste score te komen (dus b.v. 0 fouten). Ik probeerde dit op te lossen met sum squared error, nou heb ik alleen eerlijk gezegd geen flauw benul hoe ik kan bepalen welke instances ik nodig zou moeten hebben om er voor te zorgen dat de error laag blijft.
Ik heb dit al op een experimentele wijze opgelost (simpelweg random setje instances nemen en kijken of de methode erop coefficienten vindt die 0 error oplevert), maar er zou ook een theoretische methode moeten zijn om dit uit te zoeken. Daarbij werd me verteld dat ik partieel differentieren moest gebruiken. En dat als alle partieel differenties gelijk aan 0 zijn je de coefficients hebt gevonden want dan heb je 0 error. Het probleem nu alleen is, hoe haal ik hiermee eruit welke instances ik moet hebben? Mijn differentieren knobbel is daarbij wat verroest, maar ik kwam ermee dat (x-y)^2 differentieert naar df/dx: 2x-2y en df/dy: 2y-2x en d^2f/dxdy: -2 (?).
Ik heb al overal en nergens gezocht, boek doorgelezen, meerdere sites over linear regression gelezen en ik kan het gewoon niet vinden :/
Elk klein beetje help (als je weet hoe je met behulp uit een differentie kunt bepalen welke instances je moet hebben bijvoorbeeld) is van harte welkom.
Ik heb zeg maar een data set met 6 attributes die allemaal numeriek zijn.
Het idee is dat je 5 coefficienten vindt die de dataset zeg maar goed fitten. Die heb ik dus gevonden, nou heb ik alleen een ander probleem waarmee ik zit. Het gaat over de sufficient/necessary number of instances die je nodig moet hebben om aan je beste score te komen (dus b.v. 0 fouten). Ik probeerde dit op te lossen met sum squared error, nou heb ik alleen eerlijk gezegd geen flauw benul hoe ik kan bepalen welke instances ik nodig zou moeten hebben om er voor te zorgen dat de error laag blijft.
Ik heb dit al op een experimentele wijze opgelost (simpelweg random setje instances nemen en kijken of de methode erop coefficienten vindt die 0 error oplevert), maar er zou ook een theoretische methode moeten zijn om dit uit te zoeken. Daarbij werd me verteld dat ik partieel differentieren moest gebruiken. En dat als alle partieel differenties gelijk aan 0 zijn je de coefficients hebt gevonden want dan heb je 0 error. Het probleem nu alleen is, hoe haal ik hiermee eruit welke instances ik moet hebben? Mijn differentieren knobbel is daarbij wat verroest, maar ik kwam ermee dat (x-y)^2 differentieert naar df/dx: 2x-2y en df/dy: 2y-2x en d^2f/dxdy: -2 (?).
Ik heb al overal en nergens gezocht, boek doorgelezen, meerdere sites over linear regression gelezen en ik kan het gewoon niet vinden :/
Elk klein beetje help (als je weet hoe je met behulp uit een differentie kunt bepalen welke instances je moet hebben bijvoorbeeld) is van harte welkom.


Wat een rare manier, om partiële afgeleiden te pakken. ik zou eerder naar lineaire algebra kijken.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Zij X een open verzameling. Is de afsluiting van het inwendige van een verzameling X dan een deelverzameling van X?


Ja om coefficienten te vinden enzo is lineaire algebra prima, het is alleen hoe haal ik hieruit welke instances ik moet hebben? De vraag lijkt wel incompleet, want er staat niet bij of ik een aantal moet noteren of specifieke instances moet nemen. Daarbij weet ik niet of ik de coefficienten bij voorbaat al mag invullen, aangezien als ik al de coefficienten mag gebruiken die voor perfecte score kan gebruiken, kan ik net zo goed 1 instance zeggen, het is alleen dat als je 1 instance pakt en je moet de coefficienten juist vinden, dan heb je goeie kans dat je niet dezelfde coefficienten vindt. En daar ben ik dus naar op zoek, ik snap wel dat partial derivatives daarbij zouden moeten helpen om aan te geven dat je nulpunten vindt, maar om dan te zeggen welke instances?quote:Op woensdag 31 maart 2010 08:22 schreef GlowMouse het volgende:
Wat een rare manier, om partiële afgeleiden te pakken. ik zou eerder naar lineaire algebra kijken.
Klopt mijn partieel differentieren overigens?
Ja, ik heb al al het andere af en ik wil dit ook oplossen op een andere manierquote: