SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
D'oh. Niet goed gelezen. Dan ga ik het nog maar een keer zelf proberen. Was er eigenlijk gewoon vanuit gegaan dat het wel zou kloppen. Nou ik ga het weer proberen, thanks!
"Reality is an illusion created by a lack of alcohol."
Ik heb volgens mij nu net bewezen dat het niet kan kloppen, maar ik moet bewijzen dat het wel klopt dus er moet ergens een foutje zitten:
We stellen an = 3n^2 - 1 dit moet dus deelbaar zijn door 2n+2
We vullen in n+1:
32^(n+1) - 1 moet deelbaar zijn door 2n+3 = 2 * 2n+2
32^n * 2 - 1 = 32^n * 32^n - 1
Hier loop ik een beetje vast, je zou iets van de vorm:
an(32^n) + 32^n
kunnen construeren maar ik zie niet zo goed wat ik daarmee opschiet.
We stellen an = 3n^2 - 1 dit moet dus deelbaar zijn door 2n+2
We vullen in n+1:
32^(n+1) - 1 moet deelbaar zijn door 2n+3 = 2 * 2n+2
32^n * 2 - 1 = 32^n * 32^n - 1
Hier loop ik een beetje vast, je zou iets van de vorm:
an(32^n) + 32^n
kunnen construeren maar ik zie niet zo goed wat ik daarmee opschiet.
"Reality is an illusion created by a lack of alcohol."
Rechts staat een verschil van 2 kwadraten. Doe daar wat mee.quote:Op woensdag 2 december 2009 12:30 schreef Dzy het volgende:
Ik heb volgens mij nu net bewezen dat het niet kan kloppen, maar ik moet bewijzen dat het wel klopt dus er moet ergens een foutje zitten:
We stellen an = 3n^2 - 1 dit moet dus deelbaar zijn door 2n+2
We vullen in n+1:
32^(n+1) - 1 moet deelbaar zijn door 2n+3 = 2 * 2n+2
32^n * 2 - 1 = 32^n * 32^n - 1
Ik moet het volgende lineare systeem oplossen:
2x-3y=-2
2x+y= 1
3x+2y=1
Ik kwam zelf uit op:
1 0 1/8
0 1 3/4
0 0 1
Dus, x=1/8 en y=3/4.
Maar dit klopt niet, alleen voor de eerste 2 regels. Wat heb ik fout gedaan?
(Excuses voor deze waarschijnlijk zeer simpele vraag, maar ik ben zelfstanding een linear algebra boek door het nemen...Maar ik snap er nog erg weinig van. Bovendien heb ik geen antwoorden voor de opgaven.)
2x-3y=-2
2x+y= 1
3x+2y=1
Ik kwam zelf uit op:
1 0 1/8
0 1 3/4
0 0 1
Dus, x=1/8 en y=3/4.
Maar dit klopt niet, alleen voor de eerste 2 regels. Wat heb ik fout gedaan?
(Excuses voor deze waarschijnlijk zeer simpele vraag, maar ik ben zelfstanding een linear algebra boek door het nemen...Maar ik snap er nog erg weinig van. Bovendien heb ik geen antwoorden voor de opgaven.)
Je hebt niets fout gedaan, behalve concluderen dat je iets fout hebt gedaan. De conclusie had moeten zijn dat het stelsel dus geen oplossingen heeft.quote:Op woensdag 2 december 2009 16:08 schreef Siddartha het volgende:
Ik moet het volgende lineare systeem oplossen:
2x-3y=-2
2x+y= 1
3x+2y=1
Ik kwam zelf uit op:
1 0 1/8
0 1 3/4
0 0 1
Dus, x=1/8 en y=3/4.
Maar dit klopt niet, alleen voor de eerste 2 regels. Wat heb ik fout gedaan?
Ah natuurlijk!quote:Op woensdag 2 december 2009 16:13 schreef thabit het volgende:
[..]
Je hebt niets fout gedaan, behalve concluderen dat je iets fout hebt gedaan. De conclusie had moeten zijn dat het stelsel dus geen oplossingen heeft.
Leuk dat zoiets de eerste opgave is na een hele uitleg over hoe je zo'n stelsel oplost (met alleen maar voorbeelden van wél oplosbare stelsels).
Bedankt !
Meteen dan nog maar een vraag, de volgende opgave:
4x-8y = 12
3x-6y=9
-2x+4y=-6
Kan dus ook niet opgelost worden? (Ik krijg lege vectoren in de 2de en 3de rij)
[ Bericht 13% gewijzigd door Siddartha op 02-12-2009 16:20:50 ]
Alle drie de vergelijkingen zeggen hetzelfde, er zijn dus oneindig mogelijke oplossingen, namelijk x = 2y+3
"Reality is an illusion created by a lack of alcohol."
Het zal er wel mee te maken hebben dat ik vandaag al veel te lang bezig ben en ik ziek aan het worden ben maar wat bedoel je precies?quote:Op woensdag 2 december 2009 14:27 schreef thabit het volgende:
[..]
Rechts staat een verschil van 2 kwadraten. Doe daar wat mee.
"Reality is an illusion created by a lack of alcohol."
Wel, 32^n * 32^n is een kwadraat. En 1 is ook een kwadraat. Dus 32^n * 32^n - 1 is het verschil van twee kwadraten.
(a - b)(a + b) = a2 - b2, als je nu eens 1 als 12 opvat.quote:Op woensdag 2 december 2009 18:07 schreef Dzy het volgende:
[..]
Het zal er wel mee te maken hebben dat ik vandaag al veel te lang bezig ben en ik ziek aan het worden ben maar wat bedoel je precies?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Ik had hem al voor Iblis trouwens, even in my defense 
nu aan de besliskunde, weer even genoeg bewezen.
nu aan de besliskunde, weer even genoeg bewezen.
"Reality is an illusion created by a lack of alcohol."
Als dit 'niveau' van vragen niet gewenst is, hoor ik het graag.
Maar stel je hebt een systeem van vergelijkingen die allemaal uitkomen op 0. Hoe
kan je die dan oplossen?
Voorbeeld:
2x-y-3z=0
-x+2y-3z= 0
x+y+4z=0
Dus:
2 -1 -3 0
-1 2 -3 0
1 1 4 0
Dan kom ik uiteindelijk uit op:
1 0 0 0
0 1 0 0
0 0 1 0
Wat nergens op slaat....
Maar stel je hebt een systeem van vergelijkingen die allemaal uitkomen op 0. Hoe
kan je die dan oplossen?
Voorbeeld:
2x-y-3z=0
-x+2y-3z= 0
x+y+4z=0
Dus:
2 -1 -3 0
-1 2 -3 0
1 1 4 0
Dan kom ik uiteindelijk uit op:
1 0 0 0
0 1 0 0
0 0 1 0
Wat nergens op slaat....
Alle vragen zijn welkom hoor (tenzij mensen echt geen moeite doen om zelf een vinger uit te steken).quote:
Als dit 'niveau' van vragen niet gewenst is, hoor ik het graag.
Jawel, dit zegt dat x=y=z=0 de enige oplossing x. Je kiest x zo dat 1*x = 0. 0 dus.quote:Dan kom ik uiteindelijk uit op:
1 0 0 0
0 1 0 0
0 0 1 0
Wat nergens op slaat....
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
Het geitenprobleem:
Een boer heeft een cirkelvormig weiland. aan de rand van dat weiland staat een paaltje. aan dat paaltje zit een touw vast waar weer een geit aan zit. Het touw is precies zolang dat de geit precies bij de helft van het totale oppervlakte van het weiland kan. Hoe lang is het touw? Hierbij is dus niet eens een straal van het weiland gegeven.
Ik ben benieuwd of iemand van jullie hier een tip over kan geven.
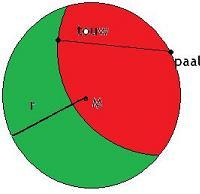
Een boer heeft een cirkelvormig weiland. aan de rand van dat weiland staat een paaltje. aan dat paaltje zit een touw vast waar weer een geit aan zit. Het touw is precies zolang dat de geit precies bij de helft van het totale oppervlakte van het weiland kan. Hoe lang is het touw? Hierbij is dus niet eens een straal van het weiland gegeven.
Ik ben benieuwd of iemand van jullie hier een tip over kan geven.
Ik moet op basis van het
Ln Y = Ln α + K^β1 + L^β2 model, de capital en labour intensive formule ontrekken.
Uitgaande van Labour intensive, is de formule daarvan Log ( Y / L ) = Log ( K / L ). Nu moet ik aangeven waarom ik op Log K / L uitkom en vroeg me af of onderstaande methode ook maar enigszins in de buurt komt ?
Ln Y = Ln α + K^β1 + L^β2 model, de capital en labour intensive formule ontrekken.
Uitgaande van Labour intensive, is de formule daarvan Log ( Y / L ) = Log ( K / L ). Nu moet ik aangeven waarom ik op Log K / L uitkom en vroeg me af of onderstaande methode ook maar enigszins in de buurt komt ?
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Ln Y = Ln α + K^β1 + L^β2
vandaar kom ik al niet op Y = L * K^β1 * L^β2 zoals je op de eerste regel zegt.
vandaar kom ik al niet op Y = L * K^β1 * L^β2 zoals je op de eerste regel zegt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik zie inderdaad net dat ik een aantal stappen heb overgeslagen,quote:Op woensdag 2 december 2009 23:15 schreef GlowMouse het volgende:
Ln Y = Ln α + K^β1 + L^β2
vandaar kom ik al niet op Y = L * K^β1 * L^β2 zoals je op de eerste regel zegt.
People once tried to make Chuck Norris toilet paper. He said no because Chuck Norris takes crap from NOBODY!!!!
Megan Fox makes my balls look like vannilla ice cream.
Megan Fox makes my balls look like vannilla ice cream.
Ik weet niet hoe je het wilt doen, maar het antwoord is nee.quote:
als je hebt
e^(-x+1) = ln e^2
mag je deze e's dan tegen elkaar wegstrepen?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
In het algemeen mag dat niet (al komt er hier toevallig wel het goede antwoord uit).quote:Op donderdag 3 december 2009 14:29 schreef poesemuis het volgende:
als je hebt
e^(-x+1) = ln e^2
mag je deze e's dan tegen elkaar wegstrepen?
ja daaromquote:Op donderdag 3 december 2009 14:44 schreef thabit het volgende:
[..]
In het algemeen mag dat niet (al komt er hier toevallig wel het goede antwoord uit).
mijn wiskundeleraar deed het op deze manier, ik vond het al vreemd
Er geldt ln ea = a, dus er staat, als je dat meeneemt: e-x+1 = 2, dat los je op door links en rechts de logaritme te nemen, en dan krijg je -x + 1 = ln 2.quote:
[..]
ja daarom
Maar ‘wegstrepen’ is dus niet echt het geval, doch het komt inderdaad, zoals thabit zegt hier toevallig goed uit.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
