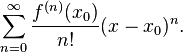W&T Wetenschap & Technologie
Een plek om te discussiŽren over wetenschappelijke onderwerpen, wetenschappelijke problemen, technologische projecten en grootse uitvindingen.



Ik was aan het denken...
Bestaan er functies met oneindig veel afgeleiden?
Zo ja, geef zo'n functie. Zo nee, waarom niet?
En in een functie met heel veel afgeleiden zoals een functie met oneindig veel afgeleiden; tot welke orde van afgeleiden kun je nog spreken over wiskundig toepasbare afgeleiden?
Bestaan er functies met oneindig veel afgeleiden?
Zo ja, geef zo'n functie. Zo nee, waarom niet?
En in een functie met heel veel afgeleiden zoals een functie met oneindig veel afgeleiden; tot welke orde van afgeleiden kun je nog spreken over wiskundig toepasbare afgeleiden?
I feel kinda Locrian today


De sinus heeft oneindig veel afgeleiden, en natuurlijk ex, om even wat bekende voorbeelden te neomen. Als d sin(x)/dx = cos(x), d cos(x)/dx = -sin(x), enz. d ex/dx = ex.
En natuurlijk verder 1/x, dat kun je ook blijven differentiŽren. Ook √x kun je blijven differentiŽren, er is namelijk maar een beperkt aantal polynomen dat uiteindelijk op 0 uitkomt (alhoewel je zou kunnen zeggen dat d0/dx = 0), namelijk die met alleen geheel-tallige positieve exponenten. Als je een polynoom hebt negatieve exponenten of gebroken exponenten, dan kun je door blijven gaan. Immers x0,73 gedifferentieerd wordt 0,73x-0,27.
Wat bedoel je met wiskundig toepasbaar eigenlijk? In zekere zin kun je zeggen, je hebt ze al nodig om smooth functions te definiŽren. Of denk je meer aan een fysische toepassing?
En natuurlijk verder 1/x, dat kun je ook blijven differentiŽren. Ook √x kun je blijven differentiŽren, er is namelijk maar een beperkt aantal polynomen dat uiteindelijk op 0 uitkomt (alhoewel je zou kunnen zeggen dat d0/dx = 0), namelijk die met alleen geheel-tallige positieve exponenten. Als je een polynoom hebt negatieve exponenten of gebroken exponenten, dan kun je door blijven gaan. Immers x0,73 gedifferentieerd wordt 0,73x-0,27.
Wat bedoel je met wiskundig toepasbaar eigenlijk? In zekere zin kun je zeggen, je hebt ze al nodig om smooth functions te definiŽren. Of denk je meer aan een fysische toepassing?
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.


Een "toepassing" is de Taylor reeksquote:Op maandag 6 juli 2009 22:55 schreef starla het volgende:
En in een functie met heel veel afgeleiden zoals een functie met oneindig veel afgeleiden; tot welke orde van afgeleiden kun je nog spreken over wiskundig toepasbare afgeleiden?
Een taylorreeks of taylorontwikkeling is in de wiskunde, speciaal in de analyse, de voorstelling of benadering van een functie als een machtreeks met coŽfficiŽnten die op een factor na de verschillende orden afgeleiden van de functie in een bepaald punt zijn. De reeks is genoemd naar de Engelse wiskundige Brook Taylor.
In het bijzonder is de taylorreeks van een functie f die in een interval |x - x0| < r oneindig vaak differentieerbaar is, de machtreeks:
Bron: zie bijv Wikipedia
Is dit wat je bedoeld met een toepassing van functies met oneindig veel afgeleiden?
Overigens is het moeilijker om functies te noemen die helemaal niet differentieerbaar zijn (op geen enkel interval), maar ze zijn er wel.
Exaudi orationem meam
Requiem aeternam dona eis, Domine.
Et lux perpetua luceat eis.
Requiem aeternam dona eis, Domine.
Et lux perpetua luceat eis.


Ook als een functie oneindig veel afgeleiden heeft op zo'n interval en de Taylorreeks op dat hele interval convergeert, dan hoeft het niet altijd zo te zijn dat de Taylorreeks naar de functiewaarden convergeert.quote:Op donderdag 9 juli 2009 20:49 schreef Oud_student het volgende:
[..]
Een "toepassing" is de Taylor reeks
Een taylorreeks of taylorontwikkeling is in de wiskunde, speciaal in de analyse, de voorstelling of benadering van een functie als een machtreeks met coŽfficiŽnten die op een factor na de verschillende orden afgeleiden van de functie in een bepaald punt zijn. De reeks is genoemd naar de Engelse wiskundige Brook Taylor.
In het bijzonder is de taylorreeks van een functie f die in een interval |x - x0| < r oneindig vaak differentieerbaar is, de machtreeks:
[ afbeelding ]
Bron: zie bijv Wikipedia
Is dit wat je bedoeld met een toepassing van functies met oneindig veel afgeleiden?
Overigens is het moeilijker om functies te noemen die helemaal niet differentieerbaar zijn (op geen enkel interval), maar ze zijn er wel.
|
|