Maar het was laat en ingewikkeld, ik was moe en stoned dus:...
Ik zoek een goed boek over de thorie van meerdere demensies. (meer dan 3 bedoel ik dan he:P)
quote:jointje maken?Op dinsdag 26 augustus 2008 12:04 schreef vaseline het volgende:
Ik zat dus laatst met een vriend te maken
http://nl.wikipedia.org/wiki/Snaartheorie
quote:Jip en Janneke en de snarentheorie...Op dinsdag 26 augustus 2008 12:14 schreef Kloppend.Mannenvlees het volgende:
Ik zou eerst eens beginnen met Jip en Janneke.
quote:praten
quote:dat dusOp dinsdag 26 augustus 2008 12:10 schreef geelkuikentje het volgende:
Dimensies bedoel je waarschijnlijk. Wat is een demensie? ik zat eerder aan dementie te denken maar dat was het vast niet
Daar moet ik weer eens heen, ben ik sinds ik wikipedia heb ontdekt niet meer geweest.
Ik weet niet of dit dubbel is: 10thdim
Anders is deze VPRO's Noorderlicht uitzending gaaf:
De theorie van alles
En je kan uit de bieb een boek van Stephen Hawkins halen.
Als je daar allemaal eens mee begint ouwe.... dan heb je wat te lullen.
[ Bericht 0% gewijzigd door MiVer op 26-08-2008 21:20:54 ]
quote:Doe die nou juist maar niet.Op dinsdag 26 augustus 2008 12:37 schreef MiVer het volgende:
Juist die site over 10th dimensie die hierboven genoemd wordt.
Grof gezegd is, wiskundig gezien, het aantal dimensies van een ‘ruimte’ gelijk aan het aantal co÷rdinaten dat je nodig hebt om een punt in die ruimte te beschrijven. Stel dat je een afbeelding hebt op de PC, dan heb je een x en y-co÷rdinaat nodig, en een r, g en b waarde en eventueel een alpha waarde om een pixel te beschrijven. Je zou dus kunnen stellen dat je voor elke pixel zes waarden nodig hebt om een punt in de tekening te beschrijven. Dan kun je zo’n afbeelding als een zesdimensionale ruimte modelleren, alhoewel het uiteindelijk intu´tief een ‘plat’ object is.
Een ander bekend voorbeeld waar intu´tie en mathematische beschrijving niet helemaal opgaan is de bol. Om een punt op de bol te beschrijven (dus niet erop of erin, alleen erop) heb je slechts twee co÷rdinaten nodig, lengte- en breedtegraad. Een bol is in die zin dus twee dimensionaal te noemen ook al heeft een bol zowel breedte als hoogte en diepte, fysisch gezien.
Als je het over tijd-ruimte hebt, kun je dit ook ook met vier co÷rdinaten beschrijven: drie voor de plek in de ruimte, en de vierde voor de tijd. Maar je kunt ook je co÷rdinaten puur geometrisch, d.w.z. ruimtelijk uitbreiden. Een bekend voorbeeld is de constructie van de hyperkubus (de vier dimensionale kubus). Zie onderstaand plaatje:
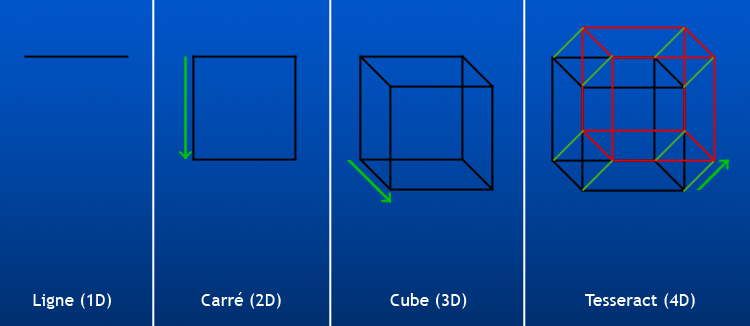
Een ÚÚn-dimensonale kubus is een lijn. Twee punten, ÚÚn verbindingsstuk. In twee dimensies krijg je een vierkant: vier punten, vier verbindingsstukken. In drie dimensies krijg je 8 punten, en 12 verbindingsstukken (ook wel ribben genoemd). Dit patroon kun je voortzetten: je construeert in feite een vierkant uit een lijn door de lijn te verdubbelen en elk punt met z'n kopie te verbinden. Het vierkant kopieer je, en je verbindt elk punt met z'n kopie, dan heb je een kubus. Hiervoor moet je ‘de hoogte in’ (in 3 dimensies is dat de ongebruikte dimensie). In vier dimensies kopieer je de kubus en verbind je elk punt weer met z'n kopie. Dit kunnen wij ons niet direct voorstellen, omdat dit in de 4e dimensie gebeurt, maar er valt wel af te leiden wat er gebeurt: de hyperkubus heeft 8 + 8 = 16 punten en 2*12 + 8 = 32 ribben. Aan elk punt grenzen vier ribben. Wat je ziet op het plaatje is echter een projectie van de hyperkubus op twee dimensies. Afhankelijk hoe de hyperkubus gedraaid is krijg je een andere projectie, zoals dat ook voor een drie dimensionale kubus geldt: zie je die recht van voren, dan zie je slechts ÚÚn vierkant, zie je ’m van opzij dan zie je twee vierkanten die overlappen.
Over deze geometrische vierde dimensie kun je ook online een film kijken, namelijk dimensions. Het behandelt stereografische projectie, en hoe Schlńfli de vierde dimensie verkende etc.
Hier onder is nog een animatie van een roterende vier-dimensionale kubus die geprojecteerd wordt in drie (en uiteindelijk in twee) dimensies. Je ziet dat ribben ‘door elkaar heen‘ gaan doordat wij in feite een soort schaduw van deze vierdimensionale kubus zien: een drie dimensionale kubus heeft ook een schaduw waarin de ribben door elkaar heen lijken te gaan.
Link naar animatie (625 kb).
Is dit je allemaal te ingewikkeld, dan kun je ook beginnen met Flatland, a romance of many dimensions, of Flatterland.
A brief history of time is wel een tof boek.
En krijgen users die Stephen Hawking zijn naam niet kunnen spellen eigenlijk ook een note?
quote:Het zou wel eens tijd worden!Op dinsdag 26 augustus 2008 20:49 schreef Haushofer het volgende:
En krijgen users die Stephen Hawking zijn naam niet kunnen spellen eigenlijk ook een note?
Dit is een wiki-artikeltje over G÷dels oplossing.

Okee hij schrijft Russell's naam fout en de grap lijkt meer op Russell's paradox dan G÷del's onvolledigheidsstelling, maar toch.
quote:Leg uit?Op dinsdag 26 augustus 2008 15:39 schreef Iblis het volgende:
Een ander bekend voorbeeld waar intu´tie en mathematische beschrijving niet helemaal opgaan is de bol. Om een punt op de bol te beschrijven (dus niet erop of erin, alleen erop) heb je slechts twee co÷rdinaten nodig, lengte- en breedtegraad. Een bol is in die zin dus twee dimensionaal te noemen ook al heeft een bol zowel breedte als hoogte en diepte, fysisch gezien.
Als er zich recht voor je een bol bevindt waarvan de kern zich precies op x=0 (breedte) en y=o (hoogte) bevindt, dan zou het punt op de kruising van x=2 en y=2 zich toch zowel aan de voorkant van de bol (de kant waar je tegenaan kijkt) als de achterkant van de bol kunnen bevinden? Heb je niet een derde (diepte-)co÷rdinaat nodig om dat te bepalen?
quote:Dat is geen handig co÷rdinatenstelsel. Ik gaf ook het voorbeeld van lengte en breedtegraad. Gegeven de nul-meridiaan en de evenaar kun je elk punt uitdrukken als het aantal graden t.o.v. die nulmeridiaan en de evenaar. Zoals dat ook op aarde gedaan wordt. B.v. Amsterdam ligt op de wereldbol op 52░22′23″N 4░53′32″O; waarbij N en O (en W en Z) eigenlijk weggelaten kunnen worden omdat je ook met negatieve getallen kunt werken. Zo ligt Lima op -12░02.6′, -77░1.7′.Op woensdag 27 augustus 2008 13:05 schreef VonHinten het volgende:
[..]
Leg uit?
Als er zich recht voor je een bol bevindt waarvan de kern zich precies op x=0 (breedte) en y=o (hoogte) bevindt, dan zou het punt op de kruising van x=2 en y=2 zich toch zowel aan de voorkant van de bol (de kant waar je tegenaan kijkt) als de achterkant van de bol kunnen bevinden? Heb je niet een derde (diepte-)co÷rdinaat nodig om dat te bepalen?
Lees ook meer op n-Sphere van Wikipedia. Dus, ook al is het een driedimensionaal object, je hebt genoeg aan de lengte en breedtegraad om een punt aan te wijzen op de bol. (Alhoewel dat de radius van de bol wat in het ongewisse laat, maar in zekere zin is die irrelevant omdat alle bolletjes op elkaar lijken.)
quote:Ik snap niet helemaal wat je bedoelt, maar ik doe een pogingOp woensdag 27 augustus 2008 13:05 schreef VonHinten het volgende:
[..]
Leg uit?
Als er zich recht voor je een bol bevindt waarvan de kern zich precies op x=0 (breedte) en y=o (hoogte) bevindt, dan zou het punt op de kruising van x=2 en y=2 zich toch zowel aan de voorkant van de bol (de kant waar je tegenaan kijkt) als de achterkant van de bol kunnen bevinden? Heb je niet een derde (diepte-)co÷rdinaat nodig om dat te bepalen?
Stel, ik neem een bol met straal r. Die bekijk ik in de 3 dimensionale ruimte ( die 3 dimensionale ruimte noem je een imbedding ) met coordinaten x,y,z. Dat doen we voor het gemak, maar belangrijk is dat een bol wiskundig gezien helemaal niet zo'n imbedding nodig heeft!
Elk punt op het oppervlak wordt beschreven door de vergelijking
x2+y2+z2 = r2
Dit is een vergelijking met 2 vrijheidsgraden; ik kan niet x,y en z onafhankelijk kiezen. Een gegeven x en y bepaalt de waarde van z. Dus het oppervlak is 2 dimensionaal. Ook al heb ik een 3 dimensionale imbedding gebruikt. Je moet zo'n boloppervlak eigenlijk los zien van de imbedding die je gebruikt.
Als we 1 coordinatensysteem aanleggen zullen we erachter komen dat we niet de gehele bol kunnen beschrijven. We hebben er minimaal 2 nodig om elk punt uniek met een coordinaat te kunnen omschrijven. Dat komt door 2 belangrijke eigenschappen die we coordinaten meegeven: nabijgelegen punten moeten beschreven worden door nabijgelegen coordinaten ( ze moeten niet zomaar een "sprong" gaan maken ) en de beschrijving moet uniek zijn.
quote:Maar we zouden natuurlijk complexe getallen kunnen gebruiken.Op woensdag 27 augustus 2008 13:16 schreef Haushofer het volgende:
Als we 1 coordinatensysteem aanleggen zullen we erachter komen dat we niet de gehele bol kunnen beschrijven. We hebben er minimaal 2 nodig om elk punt uniek met een coordinaat te kunnen omschrijven.
quote:Dan zit je nog steeds met het probleem.Op woensdag 27 augustus 2008 14:01 schreef Iblis het volgende:
[..]
Maar we zouden natuurlijk complexe getallen kunnen gebruiken.
Als ik bijvoorbeeld een variŰteit als de eenheidscirkel S1 wil parametriseren met een complex getal eix, dan heb ik minstens 2 coordinatenstelsels nodig vanwege de discontinu´teit bij x=0.
quote:Een Riemann-bol is toch een ÚÚn-dimensionale complexe variŰteit?Op woensdag 27 augustus 2008 14:25 schreef Haushofer het volgende:
[..]
Dan zit je nog steeds met het probleem.
Als ik bijvoorbeeld een variŰteit als de eenheidscirkel S1 wil parametriseren met een complex getal eix, dan heb ik minstens 2 coordinatenstelsels nodig vanwege de discontinu´teit bij x=0.
quote:Waarom "mogen ze niet zomaar een sprong maken" ?Op woensdag 27 augustus 2008 13:16 schreef Haushofer het volgende:
[..]
Ik snap niet helemaal wat je bedoelt, maar ik doe een poging
Stel, ik neem een bol met straal r. Die bekijk ik in de 3 dimensionale ruimte ( die 3 dimensionale ruimte noem je een imbedding ) met coordinaten x,y,z. Dat doen we voor het gemak, maar belangrijk is dat een bol wiskundig gezien helemaal niet zo'n imbedding nodig heeft!
Elk punt op het oppervlak wordt beschreven door de vergelijking
x2+y2+z2 = r2
Dit is een vergelijking met 2 vrijheidsgraden; ik kan niet x,y en z onafhankelijk kiezen. Een gegeven x en y bepaalt de waarde van z. Dus het oppervlak is 2 dimensionaal. Ook al heb ik een 3 dimensionale imbedding gebruikt. Je moet zo'n boloppervlak eigenlijk los zien van de imbedding die je gebruikt.
Als we 1 coordinatensysteem aanleggen zullen we erachter komen dat we niet de gehele bol kunnen beschrijven. We hebben er minimaal 2 nodig om elk punt uniek met een coordinaat te kunnen omschrijven. Dat komt door 2 belangrijke eigenschappen die we coordinaten meegeven: nabijgelegen punten moeten beschreven worden door nabijgelegen coordinaten ( ze moeten niet zomaar een "sprong" gaan maken ) en de beschrijving moet uniek zijn.
Waarom zouden polar coordinates volgens jou geen coordinaten zijn ?
Da's een beetje een arbitrair gekozen eigenschap, ik zou zeggen dat de enige belangrijke eigenschap van een coordinaat is dat het uniek is.
Met een lengte- en een breedtegraad kun je elk punt op een bol beschrijven.
Bij normale pool coordinaten wordt toch ook altijd de lengte van de vector meegegeven.
quote:Daarom had ik het over een mathematische beschrijving. Op een cirkel kun je elk punt met ÚÚn co÷rdinaat vastleggen, namelijk de hoek t.o.v. de oorsprong. Om een punt op de gehele schijf aan te wijzen heb je twee co÷rdinaten nodig.Op woensdag 27 augustus 2008 14:54 schreef Basp1 het volgende:
Maar als jullie een punt op een bol willen beschrijven is dat niets anders dan een puntje op dat vlak en heeft totaal nog geen z diepte in dit geval. (dus nog steeds 2d) Ook al is de oppervlakte rond.
Bij normale pool coordinaten wordt toch ook altijd de lengte van de vector meegegeven.
quote:Net zoals je op een lijn elk punt met 1 coordinaat kan vast leggen.Op woensdag 27 augustus 2008 15:04 schreef Iblis het volgende:
[..]
Daarom had ik het over een mathematische beschrijving. Op een cirkel kun je elk punt met ÚÚn co÷rdinaat vastleggen, namelijk de hoek t.o.v. de oorsprong. Om een punt op de gehele schijf aan te wijzen heb je twee co÷rdinaten nodig.
Een cirkel is niets anders dan een lijn die rond loopt.
Een bol vlak is niets anders als een plat vlak wat gebold is. (wanneer we het over dimensies hebben) (tjeempie wat klinkt dat krom wat ik heb getypt)
quote:Maar dat hoeft dus niet als de radius van de bol bekend is, of als je een plek op het oppervlak van een bol wilt aangeven.Op woensdag 27 augustus 2008 14:54 schreef Basp1 het volgende:
Maar als jullie een punt op een bol willen beschrijven is dat niets anders dan een puntje op dat vlak en heeft totaal nog geen z diepte in dit geval. (dus nog steeds 2d) Ook al is de oppervlakte rond.
Bij normale pool coordinaten wordt toch ook altijd de lengte van de vector meegegeven.
De bol kan zo groot of klein zijn als je wilt, maar om een plek op het oppervlak aan te geven heb je maar 2 coordinaten nodig - relatief ten opzichte van de oorsprong van de bol natuurlijk.
Als ik jou de 2 coordinaten van amsterdam geef, en een globe - zoek je dan op het oppervlak van de globe, of kun je amsterdam niet vinden omdat je niet weet hoe diep amsterdam onder de grond zit, of hoe ver het in de lucht hangt ?
quote:Juist, en dat zeg ik ook, dus wat is de discussie eigenlijk?Op woensdag 27 augustus 2008 15:30 schreef Basp1 het volgende:
[..]
Net zoals je op een lijn elk punt met 1 coordinaat kan vast leggen.
Een cirkel is niets anders dan een lijn die rond loopt.
Een bol vlak is niets anders als een plat vlak wat gebold is. (wanneer we het over dimensies hebben) (tjeempie wat klinkt dat krom wat ik heb getypt)
quote:Ja. Maar de dimensionaliteit zegt zover ik weet weinig over hoeveel charts je nodig hebt om een variŰteit te bedekken.Op woensdag 27 augustus 2008 14:39 schreef Iblis het volgende:
[..]
Een Riemann-bol is toch een ÚÚn-dimensionale complexe variŰteit?
quote:Omdat coordinatentransformaties gegeven worden door diffeomorphismes. Dat is niet een arbitrair gekozen eigenschap, maar juist een heel belangrijke.Op woensdag 27 augustus 2008 14:41 schreef L.Denninger het volgende:
[..]
Waarom "mogen ze niet zomaar een sprong maken" ?
Da's een beetje een arbitrair gekozen eigenschap, ik zou zeggen dat de enige belangrijke eigenschap van een coordinaat is dat het uniek is.
-5 graden is hetzelfde als 355 graden.
Verder is het bij mijn weten geen vaste voorwaarde om iets een coordinatensysteem te mogen noemen.
http://en.wikipedia.org/wiki/Coordinate_system
quote:In mathematics and its applications, a coordinate system is a system for assigning an n-tuple of numbers or scalars to each point in an n-dimensional space.
quote:Hoe bedoel je dit. Als ik met polaire coordinaten werk en de hoek van 1 van de assen verdraait een klein beetje verspringt het punt op het vlak toch niet zomaar.Op woensdag 27 augustus 2008 16:48 schreef L.Denninger het volgende:
Door de eigenschap van polaire coordinaten kan het zo zijn dat aan de ene kant de coordinaten een enorme sprong maken, maar er toch sprake kan zijn van "diffeomorphisme" (bij gebrek aan een nederlands woord, je hebt 'm zeker uit het engels vertaald ?), toch ?
quote:Ow je bedoelt dat je zowel het als -5 graden als 355 graden kan aanduiden. Maar heeft het diffeomorphsime niet meer te maken met de beschrijving van het vlak ipv de defenitie van de hoeken-5 graden is hetzelfde als 355 graden.
quote:Op mijn WTB opleiding heb ik ooit lang geleden geleerd dat we voor de 3 dimensionaal systeem de coordinaten met 3 verschillende coordinaten systemen kunnen weergeven.Verder is het bij mijn weten geen vaste voorwaarde om iets een coordinatensysteem te mogen noemen.
http://en.wikipedia.org/wiki/Coordinate_system
xyz, polar en cilinderisch
quote:Wat een coordinatensysteem is, hangt af van waar je het over hebt. Een gradiŰnt wordt bv ook wel es een vector genoemd, terwijl dat het eigenlijk niet is als je onderscheid maakt tussen vectoren en covectoren.Op woensdag 27 augustus 2008 16:48 schreef L.Denninger het volgende:
Door de eigenschap van polaire coordinaten kan het zo zijn dat aan de ene kant de coordinaten een enorme sprong maken, maar er toch sprake kan zijn van "diffeomorphisme" (bij gebrek aan een nederlands woord, je hebt 'm zeker uit het engels vertaald ?), toch ?
-5 graden is hetzelfde als 355 graden.
Verder is het bij mijn weten geen vaste voorwaarde om iets een coordinatensysteem te mogen noemen.
http://en.wikipedia.org/wiki/Coordinate_system
[..]
Als je het over topologische ruimtes hebt, is een coordinatenfunctie f(p) gedefinieerd als een homeomorfisme van je variŰteit M naar de ruimte Rn. Als ik twee verschillende charts heb, dan eis ik dat de overgang tussen die twee zich fatsoenlijk moet gedragen. Dat betekent dat ik een differentieerbare structuur aanleg. In 1 coordinatensysteem mag het niet zo zijn dat als ik van een coordinaat naar een nabijgelegen coordinaat ga, de boel plotselinge sprongen gaat maken; dat impliceert een discontinu´teit.
Een eenheidscirkel kan bijvoorbeeld geparametriseerd worden met een hoek f. Ga es in f=0 zitten, dus het punt wat ik definieer als "0 graden". Als ik nu een willekeurig klein stukje naar tegen de klok inga, dan ga ik naar een stukje 0-e, oftewel 359+... graden. Ook al liggen die twee punten willekeurig dicht opelkaar, de coordinaten liggen een heel stuk uitmekaar. Er is een discontinu´teit in dit punt. Dat betekent dat ik minstens 2 coordinatenstelsels nodig heb om de hele cirkel te beschrijven.
Ik ken het Nederlandse woord voor "chart" niet zo goed, maar een "chart" is een setje {Ui,f}, waarbij Ui een open deelverzameling is van M. Als je alle Ui 's verenigt, moet je M weer terugkrijgen. De Ui's bedekken M dus.
Je noemde de poolcoordinaten al, maar daar gaat het bijvoorbeeld mis bij r=0. Dat is eenvoudig na te gaan door de Jacobiaan uit te rekenen. Het punt (r=0, phi) voor willekeurige phi komt overeen met de oorsprong, en dus heb je geen unieke beschrijving meer.
quote:Ik snap opeens waar de verwarring vandaan komt; een complexe variŰteit M is natuurlijk gedefinieerd via homomorfismes vanuit de Ui naar een open verzameling van Cm; m is dan de complexe dimensie van M, terwijl 2m de "ware dimensie" van M is.Op woensdag 27 augustus 2008 14:39 schreef Iblis het volgende:
[..]
Een Riemann-bol is toch een ÚÚn-dimensionale complexe variŰteit?
Met waarneming kom je op dimensie 1,2,3.
Til je jezelf daaruit, kom je op een ander niveau, een andere dimensie.
Ik geloof zelf dat tijdreizen mogelijk is. Fysiek nog niet, maar dat is kwestie van tijd en techniek.