SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Hmm, ik snap het niet helemaal.quote:Op zondag 22 mei 2016 21:30 schreef thabit het volgende:
De restterm is es/5!, waar s ergens tussen a en x ligt (maar je weet niet waar precies).
Is het interval waarop je je Taylorpolynoom bekijkt (en dus de 'maximale waarde' voor de n+1'ste afgeleide van f(x) die hieruit volgt) per definitie gelijk aan het verschil tussen je x-waarde en je a-waarde?


Het interval is het interval tussen a en x. Het verschil tussen x en a is een getal, en een interval is dat niet.


Ah oké, dat bedoelde ikquote:Op zondag 22 mei 2016 21:57 schreef thabit het volgende:
Het interval is het interval tussen a en x. Het verschil tussen x en a is een getal, en een interval is dat niet.
Maar waarom zouden ze dan e^1 als maximale waarde stellen? Het interval zou immers gelijk zijn aan [-1,0] en aangezien e^x strikt stijgend is, is e^0 de maximale waarde.


Ze bekijken denk ik alles wat hooguit |x-a| van a afligt of zo. Dan krijg je [-1,1] in plaats van [-1,0].quote:Op zondag 22 mei 2016 22:17 schreef ulq het volgende:
[..]
Ah oké, dat bedoelde ik
Maar waarom zouden ze dan e^1 als maximale waarde stellen? Het interval zou immers gelijk zijn aan [-1,0] en aangezien e^x strikt stijgend is, is e^0 de maximale waarde.


Ik heb weer een nieuwe uitdaging. Dit is een zeer vergelijkbare formule:quote:Op dinsdag 26 april 2016 03:52 schreef Riparius het volgende:
[..]
Goed, je wil dus gewoon D2 uitdrukken in D1, D3 en D13. Kennelijk zit je een beetje te pielen met Excel, maar dan nog matchen je haakjes alweer niet, en bovendien is het onzinnig om eerst de vierkantswortel te trekken uit D1(1−D1) en het resultaat dan direct weer te kwadrateren.
Wat je kennelijk bedoelt is
Maar die haakjesorgie is hier overbodig aangezien we dit kunnen schrijven als
Nu delen we beide leden door D3 en vermenigvuldigen we tevens beide leden met D22 en dan hebben we
Aangenomen dat D2 positief is vinden we zo dus door de vierkantswortel te nemen van beide leden dat
Laten we nog even de proef op de som nemen door D13 = 2, D1 = 0,02 en D3 = 9800 in te vullen, dan vinden we
Voilà.
Het Excel orgineel:
=D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
Op basis van jouw breuk vorige keer kan ik hier het volgende van malen (ik heb mijn best gedaan dit keer TeX te gebruiken):
Hierbij moet vermeld worden dat:
L3 uitschrijven in de orginele formule ging helaas niet, dan werd de breuk te lang en kapte hij hem af.
Nu is de vraag wederom:
Omdat er nu nog meer onbekenden rechts staan, heb ik echt geen flauw idee hoe ik heb moet oplossen.


Deze formule is leesbaar, maar je hoeft geen externe server te gebruiken om TeX te gebruiken op FOK. Alles wat je hoeft te doen is de TeX tags gebruiken. Dus, bijvoorbeeld, als je dit in je bericht opneemt:quote:Op woensdag 25 mei 2016 22:36 schreef Varr het volgende:
[..]
Ik heb weer een nieuwe uitdaging. Dit is een zeer vergelijkbare formule:
Het Excel orgineel:
=D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
Op basis van jouw breuk vorige keer kan ik hier het volgende van malen (ik heb mijn best gedaan dit keer TeX te gebruiken):
[ afbeelding ]
| 1 | [tex]a = \frac{b}{c}[/tex] |
dan krijg je
Wat is hier staat is voor mij onleesbaar. Ik zie alleen een lange string van ogenschijnlijk willekeurige karakters.quote:Hierbij moet vermeld worden dat:
[snip]
Dat is niet zo. Je kunt je betrekking herleiden tot een kwadratische vergelijking in L3. Weet je hoe je kwadratische vergelijkingen op kunt lossen?quote:L3 uitschrijven in de orginele formule ging helaas niet, dan werd de breuk te lang en kapte hij hem af.
Dit is weer onleesbaar.quote:Nu is de vraag wederom:
[snip]
Je wil kennelijk L3 uitdrukken in je overige variabelen. Hoeveel variabelen dat zijn maakt niet uit, want zoals gezegd kun je je betrekking herleiden tot een kwadratische vergelijking in L3 en daarvan kun je de oplossingen uitdrukken in de coëfficiënten van de vergelijking met behulp van de abc-formule. Dan moet je wel nagaan onder welke voorwaarden de discriminant van je vergelijking niet-negatief is en bekijken welk van de twee oplossingen je moet hebben als er bijvoorbeeld een positieve en een negatieve oplossing is en je alleen geïnteresseerd bent in de positieve oplossing.quote:Omdat er nu nog meer onbekenden rechts staan, heb ik echt geen flauw idee hoe ik het moet oplossen.
[ Bericht 0% gewijzigd door Riparius op 26-05-2016 04:20:28 ]


Excuus, nu wel zichtbaar?quote:Op woensdag 25 mei 2016 23:31 schreef Riparius het volgende:
[..]
Deze formule is leesbaar, maar je hoeft geen externe server te gebruiken om TeX te gebruiken op FOK. Alles wat je hoeft te doen is de TeX tags gebruiken. Dus, bijvoorbeeld, als je dit in je bericht opneemt:
[ code verwijderd ]
dan krijg je
[..]
Wat is hier staat is voor mij onleesbaar. Ik zie alleen een lange string van ogenschijnlijk willekeurige karakters.
[..]
Dat is niet zo. Je kunt je betrekking herleiden tot een kwadratische vergelijking in L3. Weet je hoe je kwadratische vergelijkingen op kunt lossen?
[..]
Dit is weer onleesbaar.
[..]
Je wil kennelijk L3 uitdrukken in je overige variabelen. Hoeveel variabelen dat zijn maakt niet uit, want zoals gezegd kun je je betrekking herleiden tot een kwadratische vergelijking in L3 en daarvan kun je de oplossingen uitdrukken in de coëfficiënten van de vergelijking met behulp van de abc-formule. Dan moet je wel nagaan onder welke voorwaarden de discriminant van je vergelijking niet-negatief is en bekijken welk van de twee oplossingen je moet hebben als er bijvoorbeeld een positieve en een negatieve oplossing is en je alleen geïnteresseerd bent in de positieve oplossing.
Orginele Excel formule:
D3 =D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
Versimpeld in TeX:
Waar:
Het vraagstuk, als ik D2 als onbekende wil hebben i.p.v. D3, hoe wordt de formule dan?


Nu kom je weer net als vorige week pas met de juiste vraag nadat er al gereageerd is. Probeer de volgende keer je vraag te stellen in je eerste bericht...quote:Op donderdag 26 mei 2016 09:33 schreef Varr het volgende:
[..]
Excuus, nu wel zichtbaar?
Orginele Excel formule:
D3 =D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
Versimpeld in TeX:
Waar:
Het vraagstuk, als ik D2 als onbekende wil hebben i.p.v. D3, hoe wordt de formule dan?
Laat dat excel nu eens even helemaal weg en stel gewoon de vraag.
Je tex komt totaal niet overeen met je excel formule. Dat kan je zelf toch ook zien?
En je twee links zijn nog steeds allemaal tekens.
Kom met:
Ik heb de vergelijking a = f(b, c, d, etc.)
En ik wil b als een functie van a, c, d, etc. schrijven.
En zorg er nu wel voor dat je formule klopt, dat Riparius je straks niet weer een uitgebreid antwoord geeft op een andere vraag dan je wil weten.


De orginele formule laat ik liever niet weg, dan ben ik bang dat het omzetten naar TeX al fout gaat.quote:Op donderdag 26 mei 2016 10:56 schreef t4rt4rus het volgende:
[..]
Nu kom je weer net als vorige week pas met de juiste vraag nadat er al gereageerd is. Probeer de volgende keer je vraag te stellen in je eerste bericht...
Laat dat excel nu eens even helemaal weg en stel gewoon de vraag.
Je tex komt totaal niet overeen met je excel formule. Dat kan je zelf toch ook zien?
En je twee links zijn nog steeds allemaal tekens.
Kom met:
Ik heb de vergelijking a = f(b, c, d, etc.)
En ik wil b als een functie van a, c, d, etc. schrijven.
En zorg er nu wel voor dat je formule klopt, dat Riparius je straks niet weer een uitgebreid antwoord geeft op een andere vraag dan je wil weten.
Orginele Excel formule:
D3 =D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
Orgineel in TeX:
Hier is:
Ik wil weten:
De eerste stap in het versimpelen (o.b.v. de hulp Riparius van vorige keer, met een bijna dezelfde formule) is volgens mij:


En wat kan je dan met D13 en die constanten doen?quote:Op donderdag 26 mei 2016 15:24 schreef Varr het volgende:
[..]
Orgineel in TeX:
Hier is:
Ik wil weten:
De eerste stap in het versimpelen (o.b.v. de hulp Riparius van vorige keer, met een bijna dezelfde formule) is volgens mij:
Klopt trouwens nog geen klote van die wortel en kwadraat.


De vragensteller maakt niet duidelijk wat al die variabelen voorstellen en hoe hij tot zijn formule is gekomen en wat hij ermee wil bereiken. Dat zou hij eigenlijk wel moeten doen.quote:Op donderdag 26 mei 2016 19:31 schreef t4rt4rus het volgende:
[..]
En wat kan je dan met D13 en die constanten doen?
In het algemeen heb je voor elke reële xquote:Klopt trouwens nog geen klote van die wortel en kwadraat.
zodat het niet evident is dat de vierkantswortel uit dat kwadraat van zijn uitdrukking onder zijn wortelteken weer gelijk is aan die uitdrukking. Kennelijk zijn al zijn grootheden positief, maar daarmee is nog niet gezegd dat
ook steeds positief is.


quote:Op dinsdag 26 april 2016 03:52 schreef Riparius het volgende:
[..]
Goed, je wil dus gewoon D2 uitdrukken in D1, D3 en D13. Kennelijk zit je een beetje te pielen met Excel, maar dan nog matchen je haakjes alweer niet, en bovendien is het onzinnig om eerst de vierkantswortel te trekken uit D1(1−D1) en het resultaat dan direct weer te kwadrateren.
Wat je kennelijk bedoelt is
Maar die haakjesorgie is hier overbodig aangezien we dit kunnen schrijven als
Nu delen we beide leden door D3 en vermenigvuldigen we tevens beide leden met D22 en dan hebben we
Aangenomen dat D2 positief is vinden we zo dus door de vierkantswortel te nemen van beide leden dat
Laten we nog even de proef op de som nemen door D13 = 2, D1 = 0,02 en D3 = 9800 in te vullen, dan vinden we
Voilà.
De formule is niet van mezelf, het is een berekening om een sample size te berekenen voor een experiment.quote:Op donderdag 26 mei 2016 19:49 schreef Riparius het volgende:
[..]
De vragensteller maakt niet duidelijk wat al die variabelen voorstellen en hoe hij tot zijn formule is gekomen en wat hij ermee wil bereiken. Dat zou hij eigenlijk wel moeten doen.
[..]
In het algemeen heb je voor elke reële x
zodat het niet evident is dat de vierkantswortel uit dat kwadraat van zijn uitdrukking onder zijn wortelteken weer gelijk is aan die uitdrukking. Kennelijk zijn al zijn grootheden positief, maar daarmee is nog niet gezegd dat
ook steeds positief is.
De formule is bijna gelijk aan mijn vorige:
vorige
D3 = D13*(16*POWER(SQRT(D1(1-D1)/D1*D2);2)
huidige
D3 =D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
De vorige formule is toen als volgt opgelost:
Omdat de formule (for the untrained eye) zo weinig verschild, had ik verwacht dat ik deze op dezelfde manier (met jou stappen) kon oplossen. Echter omdat ik nu met D2 boven de breuk zit, weet ik niet hoe ik verder moet. Indien er nog informatie mist hoor ik het graag.


Zit die D1*D2 in de noemer onder de wortel of niet?
En wat heb je zelf al geprobeerd?
Als je alleen het antwoord wil kan je het net zo goed in Mathematica gooien.
En wat heb je zelf al geprobeerd?
Als je alleen het antwoord wil kan je het net zo goed in Mathematica gooien.


Aangezien L3 afhangt van D2 moet je beginnen in je formule L3 te vervangen door D1(1 + D2) omdat je anders alleen een uitdrukking voor D2 af kunt leiden waarin L3 voorkomt, en dan kun je D2 nog steeds niet berekenen, omdat je immers L3 niet kent zonder D2 te kennen.quote:Op vrijdag 27 mei 2016 09:36 schreef Varr het volgende:
[..]
[..]
De formule is niet van mezelf, het is een berekening om een sample size te berekenen voor een experiment.
De formule is bijna gelijk aan mijn vorige:
vorige
D3 = D13*(16*POWER(SQRT(D1(1-D1)/D1*D2);2)
huidige
D3 =D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
De vorige formule is toen als volgt opgelost:
Omdat de formule (for the untrained eye) zo weinig verschilt, had ik verwacht dat ik deze op dezelfde manier (met jou stappen) kon oplossen. Echter omdat ik nu met D2 boven de breuk zit, weet ik niet hoe ik verder moet. Indien er nog informatie mist hoor ik het graag.
Dit maakt dat deze opgave niet vergelijkbaar is met je vorige, maar een stuk lastiger. Je krijgt namelijk na herleiding een vierkantsvergelijking in D2 waarvan de coëfficiënten uitdrukkingen zijn in D1, D3, D13 en je constante C = (1,6449 + 0,84162)2.
Onder de aanname dat al je grootheden positief zijn en tevens onder de aanname dat (1 − D1) + L3(1 − L3) niet-negatief is zou je dan uit moeten komen op
Ga nu eerst maar eens netjes je uitdrukking herleiden om op deze vierkantsvergelijking in D2 uit te komen. Dat is louter elementaire algebra en daarmee niet moeilijk maar wel wat werk (wat ik dus ook heb gedaan). De volgende stap is dan het oplossen van deze vierkantsvergelijking, maar dat levert geen prettig hanteerbare uitdrukkingen op voor D2. Onder de aanname dat al je grootheden positief zijn kun je al zien dat er voor 0 < D1 < 1 één positieve oplossing zal zijn, aangezien het product van de beide oplossingen van deze vierkantsvergelijking dan negatief is omdat dit immers gelijk is aan (D12 − 1)/D12D22.


Ik moet de afgeleide uit de volgende functie halen: H(u) = 1/2u + 1/(wortel van u) + 3. Ik ben hier al de hele middag mee bezig maar kom er gewoon niet uit. Heb dan ook al 6 jaar geen wiskunde gehad dus... Kan iemand me hiermee helpen?
Shake with your right hand but hold a rock in the left.


Het is handig om 1/(wortel van u) eerst als een macht van u te schrijven.quote:Op vrijdag 10 juni 2016 18:13 schreef Teydelyk het volgende:
Ik moet de afgeleide uit de volgende functie halen: H(u) = 1/2u + 1/(wortel van u) + 3. Ik ben hier al de hele middag mee bezig maar kom er gewoon niet uit. Heb dan ook al 6 jaar geen wiskunde gehad dus... Kan iemand me hiermee helpen?
Daarna kun je de gewone regel voor differentieren toepassen.


Bedankt!quote:Op vrijdag 10 juni 2016 18:17 schreef Lokasenna het volgende:
[..]
Het is handig om 1/(wortel van u) eerst als een macht van u te schrijven.
Daarna kun je de gewone regel voor differentieren toepassen.
Shake with your right hand but hold a rock in the left.


Ik heb even een kort vraagje, als ik de volgende formules op mijn gr(casio 9860) invoer bij graph.
Y1=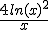
Y2 =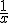
krijg ik dmv isct de punten x= -1.133 en x=1.133, terwijl ik met algebraïsche berekeningen uitkom op x=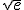 en x=
en x= 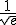 . Het antwoordenboek geeft dezelfde antwoorden als waar ik op uit kwam, weet er iemand wat ik verkeerd doe ik op mijn gr?
. Het antwoordenboek geeft dezelfde antwoorden als waar ik op uit kwam, weet er iemand wat ik verkeerd doe ik op mijn gr?
Y1=
Y2 =
krijg ik dmv isct de punten x= -1.133 en x=1.133, terwijl ik met algebraïsche berekeningen uitkom op x=


Heel eenvoudig: je toetst kennelijk ln(x²) in daar waar je (ln(x))² bedoelt. Vergelijk dit met dit.quote:Op zaterdag 11 juni 2016 16:16 schreef kura-kura het volgende:
Ik heb even een kort vraagje, als ik de volgende formules op mijn gr(casio 9860) invoer bij graph.
Y1=
Y2 =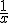
krijg ik dmv isct de punten x= -1.133 en x=1.133, terwijl ik met algebraïsche berekeningen uitkom op x=en x=
. Het antwoordenboek geeft dezelfde antwoorden als waar ik op uit kwam, weet er iemand wat ik verkeerd doe ik op mijn gr?


2^-x = 2^(2 1/2)
-x = 2 1/2
Hoe werkt dit? Hoe wordt het bovenstaande het onderste
-x = 2 1/2
Hoe werkt dit? Hoe wordt het bovenstaande het onderste
Shake with your right hand but hold a rock in the left.


Heel eenvoudig: zij a een positief reëel getal groter dan één en p en q twee andere (reële) grootheden. Als je nu hebtquote:Op maandag 13 juni 2016 13:21 schreef Teydelyk het volgende:
2^-x = 2^(2 1/2)
-x = 2 1/2
Hoe werkt dit? Hoe wordt het bovenstaande het onderste
dan is
Je kunt gemakkelijk zien waarom dit zo is: p kan niet kleiner zijn dan q, want dan zou ap ook kleiner zijn dan aq en dat is niet zo, want er is gegeven dat ap = aq. Omgekeerd kan p ook niet groter zijn dan q, want dan zou ap ook groter zijn dan aq en dat is evenmin het geval. Dus blijft er maar één mogelijkheid over, namelijk dat p en q gelijk zijn.
Bovenstaande regel geldt overigens ook als a een positief reëel getal is kleiner dan 1, maar dan volgt uit p < q dat ap > aq en uit p > q dat ap < aq, zodat uit ap = aq wederom volgt dat p = q moet zijn.
Als je iets weet over functies: de functie f(x) = ax is strict monotoon stijgend op R voor a > 1 en strict monotoon dalend op R voor 0 < a < 1.


Ik weet helemaal niets van wiskunde maar ik moet voor een hobbyproject (soort puzzeltocht) een formule samenstellen en nu heb ik geen idee of het klopt. Dit is wat ik heb...
(979 – 1986 : 6) : (7 + 5) - 6
-------------------------------------
16
De uitkomst zou 3 moeten zijn, kan een van jullie wiskunde bollebozen mij vertellen of dit klopt?
PS Ik ben nieuw op FOK!, please be gentle
(979 – 1986 : 6) : (7 + 5) - 6
-------------------------------------
16
De uitkomst zou 3 moeten zijn, kan een van jullie wiskunde bollebozen mij vertellen of dit klopt?
PS Ik ben nieuw op FOK!, please be gentle


Je bedoelt kennelijkquote:
(((979 – (1986 : 6)) : (7 + 5)) - 6) : 16
Je vraag is zo niet goed te beantwoorden omdat je opgave zo ambigu is. Als je dit soort dingen intypt op een rekenmachine kan het zo maar zijn dat het ene merk rekenmachine een andere uitkomst geeft dan het andere merk rekenmachine.
Gebruik extra haakjes om de prioriteit van je bewerkingen eenduidig te maken als je je uitdrukking lineair opschrijft resp. invoert. Je kunt de uitkomst van je berekening dan controleren in WolframAlpha. Maar goed, je hebt inderdaad

 Op
Op