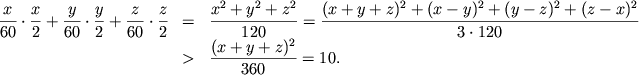WFL Wetenschap, Filosofie, Levensbeschouwing
Discussieer hier over alle aspecten van de wetenschap, filosofische problemen en zaken van levensbeschouwelijke aard.



Ja mensen, hij is er weer!
Laten we hier eens flink over gaan nadenken. Vraag 17 is in elk geval C en vraag 12 is B.quote:Vraag 1: Stel je woont op de maan en de aarde staat pal boven je. Wanneer verdwijnt de aarde aan de horizon?
A. 12 uur later.
B. 27 dagen, 7 uur en 43 minuten later.
C. Helemaal niet.
Vraag 2: Elk uur vertrekken er vanaf station Abcoude drie treinen richting Breukelen met verschillende tussenpozen. Je komt op een willekeurig tijdstip op het perron te Abcoude voor de trein naar Breukelen. Hoe lang moet je gemiddeld wachten?
A. Meer dan 10 minuten.
B. Precies 10 minuten.
C. Minder dan 10 minuten.
Vraag 3: Een verliefd stelletje kerft op twee meter boven de grond een hartje in een boom. De boom is dan vijf meter hoog. Na tien jaar is de boom tien meter hoog. Hoe hoog zit dan het ingekerfde hartje?
A. Twee meter.
B. Drie meter.
C. Vier meter.
Vraag 4: Maak in een ijsblok een kuil. Vul de kuil met water. Verwarm het geheel in de magnetron. Wat gebeurt er?
A. Het water wordt heet en het ijs blijft ijs.
B. Het water blijft koud totdat het ijs is gesmolten.
C. Het ijs ontploft.
Vraag 5: Waarom lopen pinguïns zo eigenaardig?
A. Omdat hun vetlagen in de weg zitten.
B. Omdat ze geen knieën hebben.
C. Omdat ze zulke korte poten hebben.
Vraag 6: Kun je een geslaagde foto maken van een fata morgana?
A. Ja, zonder probleem.
B. Nee, want het is gezichtsbedrog.
C. Ja, maar alleen met een infraroodcamera.
Vraag 7: Kan water branden?
A. Ja, bij zeer hoge druk gecombineerd met zeer hoge temperatuur en voldoende zuurstoftoevoer.
B. Ja, bij zeer lage druk gecombineerd met voldoende koolzuurtoevoer.
C. Nee.
Vraag 8: Waarom lijken alle pausen en bisschoppen zo op elkaar in de eerste gedrukte, geïllustreerde boeken?
A. De illustratoren mochten geen goedgelijkende portretten maken om religieuze redenen.
B. De illustratoren gebruikten voor elke geestelijke dezelfde houtsnede.
C. De illustratoren verzonnen maar wat omdat ze de geestelijken nooit hadden gezien.
Vraag 9: Een parachutespringster hangt boven zee aan haar parachute op 300 meter hoogte. Achter haar de avondzon, voor haar een regenbui. Ideale omstandigheden voor een regenboog en die ziet ze dan ook. Hoe ziet ze die?
A. Als een boog.
B. Als een horizontale band.
C. Als een cirkel.
Vraag 10: Een trampolinespringer springt met springstelten (schoenen met bladveren eronder) vanaf een stellage die één meter hoger is één keer op een trampoline. Hij zet zich zo hard mogelijk af op de trampoline. Wanneer springt hij duidelijk het hoogst?
A. Met de springstelten aan zijn voeten.
B. Met de springstelten in een rugzak.
C. Maakt niet uit.
Vraag 11: Heeft een melktand een wortel?
A. Nee, een tijdelijk gebit heeft dat niet nodig.
B. Ja, maar bij het wisselen drukt de nieuwe tand de oude wortel weg.
C. Ja, maar de wortel is zo klein dat je hem niet ziet.
Vraag 12: Je legt een bezemsteel horizontaal op je twee evenwijdig uitgestoken wijsvingers. Je beweegt rustig de ene vinger naar de andere toe. Wat gebeurt er?
A. De bezemsteel beweegt mee op de bewegende vinger totdat hij van de andere vinger afvalt
B. De bezemsteel steunt beurtelings op de ene en de andere vinger, tot die elkaar raken.
C. De bezemsteel blijft liggen op de niet bewegende vinger. De andere vinger schuift onder de bezemsteel door tot de bezemsteel kantelt.
Vraag 13: Een eend zwemt met haar jongen in een diepe sloot. Een van de kuikens dwaalt af. Moeder eend haalt het kuiken snel in. Wat is het verschil in de hoeken van de V-vormige boeggolven van moeder en jong?
A. De hoek die de moedereend maakt is scherper.
B. De hoek die de moedereend maakt is stomper.
C. Er is geen verschil.
Vraag 14: Waardoor is een rode wijnvlek op een tafelblad in het centrum lichter dan aan de randen van de vlek?
A. Bij het vallen vloeien de gekleurde deeltjes naar de randen.
B. Bij het opdrogen trekken de gekleurde deeltjes naar de randen.
C. Het is gezichtsbedrog, veroorzaakt door het kleurverschil tussen de vlek en de omgeving.
Vraag 15: Hoe komt het dat we de vage geur van een gaslek beter ruiken als we snuffelen in plaats van rustig door de neus inademen?
A. Snuffelen maakt van de constante prikkel pulsen. Dit voorkomt gewenning.
B. Snuffelen veroorzaakt wervelingen die zorgen dat de geur hoog in de neusholte dringt.
C. Het snuffelen regelt onze aandacht.
Vraag 16: Als een fotograaf zijn camera 45 graden scheef houdt, vinden we alles op de foto hinderlijk scheef staan. Maar als je je hoofd scheef houdt, heb je daar geen last van. Hoe komt dat?
A. We weten dat bomen en huizen rechtop staan.
B. Onze ogen compenseren onze hoofdbeweging door om hun kijk-as te draaien.
C. Onze hersenen corrigeren het gedraaide beeld.
Vraag 17: Bouw een toren van vierkante stoeptegels die zo ver mogelijk naar een kant overhelt. De tegels mogen alleen op elkaar gelegd worden, niet naast elkaar. Hoe ver helt hij maximaal over?
A. Precies twee tegels.
B. Ongeveer anderhalve tegel.
C. Oneindig ver.
Vraag 18: Waarom zie je in het centrum van je gezichtsveld minder sterren dan daarbuiten?
A. De randen van je gezichtsveld bestrijken een groter stuk heelal.
B. De rand van je netvlies is lichtgevoeliger dan het centrum.
C. Het is gezichtsbedrog.
Vraag 19: Een zwembad gevuld met maïzena wordt gemengd met water totdat een dikke pap ontstaat. Wat gebeurt er als je over het mengsel naar de overkant probeert te rennen?
A. Je bereikt de overkant zonder weg te zakken.
B. Na elke stap zak je dieper weg.
C. Je zakt direct weg.
Vraag 20: Als mensen een grote geestelijke inspanning verrichten dan wordt de temperatuur van hun:
A. voorhoofd aan de oppervlakte lager.
B. wangen aan de oppervlakte hoger.
C. neus lager.


hebben ze die vraag erin gedaan voor de humor...quote:Op dinsdag 29 november 2005 13:55 schreef thabit het volgende:
6 is denk ik ook A.
edit : alhoewel je natuurlijk met je camera naar de Efteling kan gaan.


noemen ze een foto morgana...quote:Op dinsdag 29 november 2005 13:55 schreef thabit het volgende:
6 is denk ik ook A.
4: B denk ik
I only tell you once. Don't fuck me, Tony. Don't you ever try to fuck me.


3 A
5 C (pinguins hebben toch knieen)
10 B
11 A(denk ik) C (volgens google)
12 B
[ Bericht 36% gewijzigd door SterkStaaltje op 29-11-2005 14:10:04 ]
5 C (pinguins hebben toch knieen)
10 B
11 A(denk ik) C (volgens google)
12 B
[ Bericht 36% gewijzigd door SterkStaaltje op 29-11-2005 14:10:04 ]


1: C - Logisch
2: B - Gemiddeld komt om de twintig minuten een trein.
Je hebt dan dus evenveel kans om meer dan 10 minuten als minder dan 10 minuten te moeten wachten.
3: ? - In ieder geval niet A, want takken groeien toch ook mee naar boven?
4: A - Uiteindelijk smelt het ijs wel, maar een magnetron maakt gebruik van de dipooleigenschap en die is groter bij vloeibaar water dan bij vast water.
5: ? - In ieder geval niet B, ze hebben wel kniën; ik denk C.
6: A
7: ? Scheikundig gezien is verbranding de vereniging van zuurstof met andere elementen. Wanneer men water (H2O) voldoende verhit (ruim 2000°C) zullen waterstof en zuurstof van elkaar scheiden en in gasvorm prima brandbaar zijn. De vraag is alleen of je het dan nog water kunt noemen. Het lijkt mij dat in dat geval H2O enkel het beginproduct is en niet hetgene dat daadwerkelijk brandt.
8: B
9: C - Een regenboog is dacht ik eigenlijk een cirkel, waarvan je de helft niet kunt zien.
10: B - Als je op een springkussen springt zul je inveren en weer omhoog veren. Als je veren onder je schoenen gaat monteren dan zul je nog wel inveren maar zodra je weer omhoog geschoten gaat worden zullen die veren alles gaan dempen. De zwaartenergie wordt omgezet in veerenergie van het springkussen. Die veerenergie zet zich weer om in veer-energie van je veren onder je schoenen. Die veren werken dus als dempers.
11: B - De wortel lost op bij het wisselen.
12: B
13: A - Moeder is sneller, dus de boeggolf zal ook scherper moeten zijn.
14: ?
15: B - Hoger in de neusholte kan je beter ruiken, dus het snuffelen en de wervelingen lijken mij bij te dragen aan meer luchtstroom langs de geurreceptoren.
2: B - Gemiddeld komt om de twintig minuten een trein.
Je hebt dan dus evenveel kans om meer dan 10 minuten als minder dan 10 minuten te moeten wachten.
3: ? - In ieder geval niet A, want takken groeien toch ook mee naar boven?
4: A - Uiteindelijk smelt het ijs wel, maar een magnetron maakt gebruik van de dipooleigenschap en die is groter bij vloeibaar water dan bij vast water.
5: ? - In ieder geval niet B, ze hebben wel kniën; ik denk C.
6: A
7: ? Scheikundig gezien is verbranding de vereniging van zuurstof met andere elementen. Wanneer men water (H2O) voldoende verhit (ruim 2000°C) zullen waterstof en zuurstof van elkaar scheiden en in gasvorm prima brandbaar zijn. De vraag is alleen of je het dan nog water kunt noemen. Het lijkt mij dat in dat geval H2O enkel het beginproduct is en niet hetgene dat daadwerkelijk brandt.
8: B
9: C - Een regenboog is dacht ik eigenlijk een cirkel, waarvan je de helft niet kunt zien.
10: B - Als je op een springkussen springt zul je inveren en weer omhoog veren. Als je veren onder je schoenen gaat monteren dan zul je nog wel inveren maar zodra je weer omhoog geschoten gaat worden zullen die veren alles gaan dempen. De zwaartenergie wordt omgezet in veerenergie van het springkussen. Die veerenergie zet zich weer om in veer-energie van je veren onder je schoenen. Die veren werken dus als dempers.
11: B - De wortel lost op bij het wisselen.
12: B
13: A - Moeder is sneller, dus de boeggolf zal ook scherper moeten zijn.
14: ?
15: B - Hoger in de neusholte kan je beter ruiken, dus het snuffelen en de wervelingen lijken mij bij te dragen aan meer luchtstroom langs de geurreceptoren.
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


18: B
kegeltjes, staafjes verhaal...
Je kunt alleen met het deel waarop je focust kleuren zien (kegeltjes). Aan de randen heb je alleen staafjes, die zien alleen grijstinten en zijn gevoeliger voor licht dan de kegeltjes.
kegeltjes, staafjes verhaal...
Je kunt alleen met het deel waarop je focust kleuren zien (kegeltjes). Aan de randen heb je alleen staafjes, die zien alleen grijstinten en zijn gevoeliger voor licht dan de kegeltjes.
Op zondag 8 maart 2009 21:38 schreef Danny het volgende:
fuck de policy. posten die hap!
fuck de policy. posten die hap!


Helaas, dit is fout. Stel dat de tussentijden x,y,z zijn. Dan is x+y+z=60 en x,y,z zijn onderling verschillend want dat is gegeven. De kans dat je op het interval van x terechtkomt is x/60 en de gemiddelde wachttijd is dan x/2. Evenzo voor y en z. De gemiddelde wachttijd is dusquote:Op dinsdag 29 november 2005 14:34 schreef Quarks het volgende:
2: B - Gemiddeld komt om de twintig minuten een trein.
Je hebt dan dus evenveel kans om meer dan 10 minuten als minder dan 10 minuten te moeten wachten.


Dan kom je toch uit op B: 10 minuten?quote:Op dinsdag 29 november 2005 14:57 schreef thabit het volgende:
[..]
Helaas, dit is fout. Stel dat de tussentijden x,y,z zijn. Dan is x+y+z=60 en x,y,z zijn onderling verschillend want dat is gegeven. De kans dat je op het interval van x terechtkomt is x/60 en de gemiddelde wachttijd is dan x/2. Evenzo voor y en z. De gemiddelde wachttijd is dus
[afbeelding]
Is het niet zo dat de minimale wachttijd is die waarbij de intervallen tussen de treinen even groot zijn?
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Er staat een > in de formule.quote:Op dinsdag 29 november 2005 15:19 schreef Quarks het volgende:
[..]
Dan kom je toch uit op B: 10 minuten?
Is het niet zo dat de minimale wachttijd is die waarbij de intervallen tussen de treinen even groot zijn?


Pathologisch voorbeeldje: stel dat de drie treinen op hetzelfde tijdstip vertrekken. Dan is de gemiddelde wachttijd een half uur.


De kleinst mogelijke gemiddelde wachttijd is 10 minuten. En dit is wanneer de treinen om de 20 minuten vertrekken. Bij elke andere vetrektijd zal de tijd alleen maar groter worden. Als de trein om het heel uur komt, om 1 over en om 2 over is de kans natuurlijk veel groter dat je moet wachten op de trein die vetrekt op het hele uur.


Sorry, overheen gelezen.quote:
Laten we de lengte van de intervallen tussen de momenten dat de trein vertrekt a, b en c noemen. a+b+c is 1 (uur). de kans om in interval a aan te komen is dus a, de kans om in interval b aan te komen is b, en de kans om in interval c aan te komen is c.
Als je aankomt in tijdsinterval a moet je gemiddeld 0.5*a wachten. Zelfde voor b en c. De gemiddelde tijd dat je staat te wachten is de kans op een van deze 3 maal de gemiddelde wachttijd van dat interval. Dus:
t (= totale wachttijd) = a*0.5*a+b*0.5*b+c*0.5*c = 0.5(a2+b2+c2)
Als a = b = c, dan wordt dit: t = 0.5*3a2.
Laten we nu een parameter d en e introduceren, zodanig dat de nieuwe vergelijking wordt :
t = 0.5((a+d+e)2+(b-d)2+(c-e)2)
a=b=c, dus t = 0.5((a+d+e)2+(a-d)2+(a-e)2)
Uitwerken geeft t = 0.5*(a2+d2+e2+2ad+2ae+2de+a2+d2-2ad+a2+e2-2ae)
=0.5*(3a2+2d2+2e2+2de)
ofwel, t = 0.5*3a2 + d2 +e2 +de
en d2 +e2 +de is altijd positief voor willekeurige d en e anders dan d=0 en e=0. Dus is de minimale wachttijd die waarbij de intervallen tussen de treinen even groot zijn.
Klopt dat?
En 3 = A: Takken zijn secundaire groei.
De delende cellen bij planten die verantwoordelijk zijn voor lengtegroei bevinden zich altijd in het topje van een boom of tak.
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Ja, volgens mij wel. In de formule die ik gaf kun je het ook zien: er staan termen (x-y)2, (y-z)2 en (z-x)2 in. Deze termen geven de verschillen in de tijden tussen de treinen aan. Hoe groter die verschillen worden, hoe groter dus ook de gemiddelde wachttijd.quote:


Ok.quote:Op dinsdag 29 november 2005 15:42 schreef thabit het volgende:
[..]
Ja, volgens mij wel. In de formule die ik gaf kun je het ook zien: er staan termen (x-y)2, (y-z)2 en (z-x)2 in. Deze termen geven de verschillen in de tijden tussen de treinen aan. Hoe groter die verschillen worden, hoe groter dus ook de gemiddelde wachttijd.
16: C
17: C - Als je genoeg tegels hebt, dan kun je de bovenste zover uit laten steken als je wilt, de totale overhang voor N tegels op een bodemtegel is somi=1->N(1/2i).
18: B - In het midden van je netvlies zitten de meeste kegeltjes (voor kleuren) en aan de randen de meeste staafjes (gevoeliger voor licht).
19: A - Moet je wel snel genoeg lopen.
20: C
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


14: C 'oud en bekend'
3: A [bomen groeien alleen in de toppen en in de breedte]
19: A [vraag me af of hetzelfde geldt voor aardappel zetmeel? Quarks?]
3: A [bomen groeien alleen in de toppen en in de breedte]
19: A [vraag me af of hetzelfde geldt voor aardappel zetmeel? Quarks?]
Rudeonline logic: "1km +1sec=1km/s"
"I don't know what your problem is, but I bet it's hard to pronounce.''
"I don't know what your problem is, but I bet it's hard to pronounce.''


Als allebei de potentiele energie bevatters perfect waren, zou er een soort van boxwedstrijd ontstaan tussen de springschoenen en de trampoline, waar ze hun energie naar elkaar uitstoten zolang ze met elkaar in contact zijn en hun "grens" niet bereikt is.quote:Op dinsdag 29 november 2005 17:30 schreef thabit het volgende:
Ik twijfel over 10. Het zou ook C kunnen zijn: wet van behoud van energie.
Ze zijn echter niet perfect dus elke keer dat de ene energie variant in de andere wordt omgezet, onstaat erwarmte.
Bij 2 veren raakt hierdoor meer energie verloren dan met 1 veer.
De kinetische energie die wordt opgewekt is alleen het gevolg van de hoogte van de sprong, en het gewicht van de springer.
Vergelijk het met golven:
In dit geval wordt de energie van de trampoline gebruikt om de golfbeweging van de springveren op te vangen.
Doordat beide een andere golfbeweging hebben heffen ze elkaar deels op, waardoor je met springveren amper omhoog komt.
* 11:15, restate my assumptions: 1. Mathematics is the language of nature. 2. Everything around us can be represented and understood through numbers. 3. If you graph these numbers, patterns emerge. Therefore: There are patterns everywhere in nature.*


Deze volg ik niet. Zoals je het opschrijft stapel je de volgende tegel met de helft op de vorige tegel. Stel dan dat je gaat stapelen met elke keer een tegel op de helft van vorige tegel. Begin daarbij links en stapel dan door naar rechts, stapel zo denkbeeldig 3 tegels op de onderste tegel. Dan is het gewicht rechts van het kantelpunt van de op een na onderste tegel groter dan dat er links gecompenseerd wordt.quote:Op dinsdag 29 november 2005 16:01 schreef Quarks het volgende:
17: C - Als je genoeg tegels hebt, dan kun je de bovenste zover uit laten steken als je wilt, de totale overhang voor N tegels op een bodemtegel is somi=1->N(1/2i).
|
|