quote:Anders leg je eerst even uit wat je er zelf van weet?Op maandag 31 mei 2004 12:35 schreef Plustus het volgende:
wie kan mij hier meer over vertellen, hoe ver is men al met deze theorie etc etc
Want ik heb geen idee waar je het over hebt namelijk.
http://www.pbs.org/wgbh/nova/elegant/program.html
hiermee kom ik vast wel een heel eind
quote:...bennie gekOp maandag 31 mei 2004 15:11 schreef OldJeller het volgende:
En anders kan je google misschien een keer gebruiken, weet je wat dat is?
Immers (geloof ik) met dat soort wiskunde is er een oneindig aantal vormen van universa mogelijk. Je spreekt immers over bouwstenen. Ik denk dat mathematici nog een stap verder moeten gaan straks zodat je een oneindig aantal mogelijkheden bundeld in 1 mathematische formule.
En hoe doe je dat? Juist, gewoon BLIJVEN uitschrijven en op een gegeven moment heb je genoeg dingen gevonden.
Klopt het een beetje wat ik zeg hier?
quote:Op maandag 31 mei 2004 16:22 schreef devilish1980 het volgende:
leuke is dat er een heleboel snaar theorieen zijn stuk of 10 hehe
quote:Die is er al. Alle stringtheorieen bleken dezelfde theorie maar dan anders bekeken te zijn.Op maandag 31 mei 2004 16:38 schreef 0d1n het volgende:
Volgens mij is men gewoon niet in staat om 1 bindende formule te vinden voor alle snaar universa.
quote:Ik weet niet precies wat je bedoelt, maar er zijn iig 11 dimensies op string-niveau, waarvan alle behalve de bekende 4 dimensies eromheengekromd zitten.Op maandag 31 mei 2004 16:38 schreef 0d1n het volgende:
Immers (geloof ik) met dat soort wiskunde is er een oneindig aantal vormen van universa mogelijk.
quote:Ik had begrepen dat het aantal (11) nog varieerde tussen de theorieen. Maar mss is mijn kennis oud.Op maandag 31 mei 2004 17:02 schreef PuR3_D4RkN355 het volgende:
Ik weet niet precies wat je bedoelt, maar er zijn iig 11 dimensies op string-niveau, waarvan alle behalve de bekende 4 dimensies eromheengekromd zitten.
In het kort (kort door de bocht that is) is het een theorie die de bouwstenen van het Universum beschrijft en de theorieen van Einstein en Newton verenigd hetgeen onmogelijk leek. Die meerdere dimensies zijn nodig om het kloppend te maken.
Met een beetje geluk hebben we binnenkort op deze manier een gefundeerde theorie waarmee we de natuurkundige eigenschappen van ons universum kunnen verklaren en dus ook een model waarmee we kunnen werken. Sommige claimen zelfs dat we dan het eindpunt bereikt hebben en dat we niks "nieuws" meer hoeven te verzinnen omdat "alles" te verklaren is met strings hence "the theory of everything". Natuurlijk blijft er nog wel genoeg te onderzoeken dan.
Mooie site met filmpjes btw.
quote:Ik denk dat het wel mogelijk is. Het feit dat er een oneindig aantal mogelijkheden zijn kun je ook door middel van kansrekening oplossen. Het antwoord van een formule is dan een bepaalde zekerheid dat iets gebeurd. Daarnaast gaat het om een paar (niet 1) formules die de ultieme bouwstenen beschrijven. Waarvan elke formule iets van een eigenschap berekent/weergeeft.Op maandag 31 mei 2004 16:38 schreef 0d1n het volgende:
Volgens mij is men gewoon niet in staat om 1 bindende formule te vinden voor alle snaar universa.
Immers (geloof ik) met dat soort wiskunde is er een oneindig aantal vormen van universa mogelijk. Je spreekt immers over bouwstenen. Ik denk dat mathematici nog een stap verder moeten gaan straks zodat je een oneindig aantal mogelijkheden bundeld in 1 mathematische formule.
1Brian Green, de kosmische symfonie. Erg mooi boek voor leken.
2 Als ik jou was, zou ik het over iets anders doen. Kwantummechanica of relativititeit. Waarom?
De snaartheorie kan nog niet worden getoetst, en dat blijft ook nog wel even zo. Bovendien steunt het erg veel op wiskundige esthetiek. QM of relatitiveit daarentegen zijn concreet, getoetst, en daar kun je als leek iets nuttigs over zeggen. Het is ook erg veel toegepast in de huidige maatschappij. Over de snaartheorie kun je erg weinig zeggen zonder wiskunde. Snaartheorie is namelijk meer wiskunde dan natuurkunde, zover ik het begrepen heb.( Alle deeltjes zijn snaren. Waarom? Ja, is na een punt het meest aannemelijke. Ach, we hebben 11 dimensie's nodig! Hoe gaan we die oprollen? Etc etc. )
Nou ja, mocht je het wel graag willen na mijn geouwehoer: Zoek es naar het snaarmodel van de sterke kernkracht, daar is het allemaal mee begonnen. Ik geloof dat één naam daarvan Vedeziano is ofzo. Veel plezier ermee ej.
quote:En QM en relativiteit zijn leuk..Op maandag 31 mei 2004 19:44 schreef Haushofer het volgende:
Als ik jou was, zou ik het over iets anders doen. Kwantummechanica of relativititeit. Waarom?
De snaartheorie kan nog niet worden getoetst, en dat blijft ook nog wel even zo. Bovendien steunt het erg veel op wiskundige esthetiek. QM of relatitiveit daarentegen zijn concreet, getoetst, en daar kun je als leek iets nuttigs over zeggen.
Vergat je erbij te zeggen
quote:Dat denk ik niet!Op maandag 31 mei 2004 17:36 schreef Plustus het volgende:
tja, zal de mens ooit 'uitgeontdekt' zijn... wie zal het weten
Ook al heb je een manier gevonden om alles in dit universum te verklaren...... snaar theorie stelt ook dat er meerdere universa zijn.... dus klaar zijn we nog lang niet!
http://superstringtheory.com/
of gewoon hier: google
quote:Ja, soms worden de mooiste dingen voor vanzelfsprekend aangenomen. Ik zal het niet weer vergetenOp maandag 31 mei 2004 22:23 schreef OldJeller het volgende:
[..]
En QM en relativiteit zijn leuk..
Vergat je erbij te zeggen
quote:Nee ik ben niet gek!Op maandag 31 mei 2004 16:20 schreef Plustus het volgende:
[..]
...bennie gek

Maar heeft TS al iets moois gevonden?
quote:1) je moet die filmpjes van elegant universe beter bekijkenOp dinsdag 1 juni 2004 15:17 schreef Haushofer het volgende:
Ik lees hier ook dingen over meerdere universa. Dat zal wel voortkomen uit het idee dat er 6 verschillende theorieen zijn, en dat ze de overkoepelende de M-theorie noemen ofzo. Maar meerdere universa, dat wist ik nog niet.
Maar heeft TS al iets moois gevonden?
2) Dit komt niet doordat er 5 verschillende versies zijn, maar omdat dit gesteld wordt omdat gravitonen dit universum kunnen verlaten en in een ander terecht komen. (dat is in iedergeval wat ik opgevangen heb...
quote:nog 2 erbij, en de klankkast-theorie, dan hebben we een gitaarOp maandag 31 mei 2004 16:22 schreef devilish1980 het volgende:
leuke is dat er een heleboel snaar theorieen zijn stuk of 10 hehe
Goed uitgelegd.
quote:Idd. Ik heb ze eergisteren allemaal gezien en door de special effects en voorbeelden zijn ze zowel leerzaam als onderhoudend tegelijk. Boek "The Elegant Universe" ook van hem als ik me niet vergis is eveneens een echte aanrader.Op woensdag 2 juni 2004 22:41 schreef Biancavia het volgende:
Die filmpjes zijn
Goed uitgelegd.
quote:Dat kan ook nog natuurlijk. Wij denken dat het universum simpel is maar het zou best kunnen dat de som van alle quarks/moleculen/objecten in dit universum nog niks is in vergelijking tot het aantal kloppende theorieen die de mens nog uit zou moeten vinden. Anderzijds denk ik wel weer dat mensen zoals hierboven al gesuggereerd is, instaat zijn mooi pakkende formules te verzinnen. Maar dan nog aardig lang bezig blijven met zoeken.Op dinsdag 1 juni 2004 09:59 schreef Wild_Snake het volgende:
Dat denk ik niet!
Wij zijn een soort van vissekom (plastik sleutelhangervorm) waar wij dan zo'n elektronen deeltje voorstellen en de vis het universum voorstelt
quote:Je kunt bewijzen dat er een maximum aantal dimensies D < oneindig is, en D(kritisch) = 10. Het aantal universa wordt ook eindig. Jammer voor Einstein want zijn postulaat: de lichtsnelheid is de maximale snelheid of equivalent: er zijn oneindig veel universa vervalt hiermee.Op maandag 31 mei 2004 16:38 schreef 0d1n het volgende:
Volgens mij is men gewoon niet in staat om 1 bindende formule te vinden voor alle snaar universa.
Immers (geloof ik) met dat soort wiskunde is er een oneindig aantal vormen van universa mogelijk. Je spreekt immers over bouwstenen. Ik denk dat mathematici nog een stap verder moeten gaan straks zodat je een oneindig aantal mogelijkheden bundeld in 1 mathematische formule.
En hoe doe je dat? Juist, gewoon BLIJVEN uitschrijven en op een gegeven moment heb je genoeg dingen gevonden.
Klopt het een beetje wat ik zeg hier?
(bv J. Polchinski in: Les Houches 1994 Summer School). Ik heb het als document beschikbaar. Niveau is postdoc. Kennis van tensor rekenen in Minkowski rumtes en op Riemann oppervlakten
is noodzakelijk). Kennis van Yang- Mills theorie helpt.
Uit deze theorie volgt o.a. dat er tachyonen zijn, fysieke deeltjes met snelheden boven de lichtsnelheid in vacuum. En daar heb ik wat moeite mee.
quote:Ik heb het in http://members.home.nl/fb.hendriks/Start/ gezet.Op zondag 6 juni 2004 19:45 schreef Haushofer het volgende:
Kun je ff een linkje naar dit document geven? Dat maximum aan Dimensie's, is dat algemeen? En hoe is de maximale snelheid gerelateerd aan het aantal universa? De max snelheid volgt toch gewoon als je de snelheidsvector in de vierdim Minkowskiruimte neemt, en er dan achter komt dat je snelheid in dit ruimte-tijd vlak altijd de lichtsnelheid is?
quote:Het maximum aan dimensies volgt uit dit model. Of het juist is?? Maar het beschrijft de resultaten van de experimenten goed.Op zondag 6 juni 2004 19:45 schreef Haushofer het volgende:
Kun je ff een linkje naar dit document geven? Dat maximum aan Dimensie's, is dat algemeen? En hoe is de maximale snelheid gerelateerd aan het aantal universa? De max snelheid volgt toch gewoon als je de snelheidsvector in de vierdim Minkowskiruimte neemt, en er dan achter komt dat je snelheid in dit ruimte-tijd vlak altijd de lichtsnelheid is?
De fase snelheid (w/k) kan veel groter zijn dan de lichtsnelheid.
De groepssnelheid (dw/dk) is maximaal de lichtsnelheid, maar volgens de snaartheorie bestaan er tachyonen en dan zou dw/dk > c kunnen zijn. Sterker, de minimum snelheid van een tachyon is de lichtsnelheid.
quote:Op zondag 6 juni 2004 15:54 schreef Yosomite het volgende:
Je kunt bewijzen dat er een maximum aantal dimensies D < oneindig is, en D(kritisch) = 10. Het aantal universa wordt ook eindig. Jammer voor Einstein want zijn postulaat: de lichtsnelheid is de maximale snelheid of equivalent: er zijn oneindig veel universa vervalt hiermee.
(bv J. Polchinski in: Les Houches 1994 Summer School). Ik heb het als document beschikbaar. Niveau is postdoc. Kennis van tensor rekenen in Minkowski rumtes en op Riemann oppervlakten
is noodzakelijk). Kennis van Yang- Mills theorie helpt.
Uit deze theorie volgt o.a. dat er tachyonen zijn, fysieke deeltjes met snelheden boven de lichtsnelheid in vacuum. En daar heb ik wat moeite mee.
Opgeslagen
Ik vrees dat het wiskundig te veel gevraagd zal zijn, maar ik zal er eens proberen door te spitten.

klik op 't plaatje voor een uitvergroting en tegelijkertijd the whole story in the New York Times
quote:Ik hoop dat de (mem)braam theorie snel overboord gezet kan worden. Niet omdat het absurd fantastisch klinkt. Je kunt er geen enkele kant mee op. Gravitonen moeten de oplossing worden van deze bizarre theorie.Op zondag 25 juli 2004 14:32 schreef Bard_Yttap het volgende:
[[url=http://graphics.nytimes.com/library/national/science/040400sci-universal-theory.A.jpg]afbeelding][/url]
klik op 't plaatje voor een uitvergroting en tegelijkertijd the whole story in the New York Times
Nou de eerste graviton moet nog steeds gevonden worden. Gravitonen zijn bijna onbetaalbaar, want het maken van de versnellers die ze moeten produceren kosten veel geld.
Ik kan beter leven met de 3d + tijd dimensie, ipv de 10 dimensies van de snarentheorie met daarbij de 3d membramen die als eilanden door een multiversum klotsen waartussen grote gaten van hyperruimtes aanwezig zijn.
quote:Welke kant wil jij dan op? The brane theorie gaat verder dan de supersnaar theorie en blijft dus interessant zolang string theory in zwang blijft. Opmerkelijk is wel dat van 't Hooft er ook niets in ziet, terwijl hij wel aan de wieg van het nog niet gevonden Higgs boson heeft gestaan. Het toeval wil nu dat de Higgs boson de eerste kandidaat voor de graviton is. Wordt de Higgs boson dus ontdekt, misschien zodra the Large Hadron Collider (LHC) in april 2005 bij CERN gereed is, dan is dat full-circle voor String-theory en Brane-theory en bye bye van 't Hooft.Op zondag 25 juli 2004 16:14 schreef Yosomite het volgende:
[..]
Ik hoop dat de (mem)braam theorie snel overboord gezet kan worden. Niet omdat het absurd fantastisch klinkt. Je kunt er geen enkele kant mee op. Gravitonen moeten de oplossing worden van deze bizarre theorie.
Nou de eerste graviton moet nog steeds gevonden worden. Gravitonen zijn bijna onbetaalbaar, want het maken van de versnellers die ze moeten produceren kosten veel geld.
Ik kan beter leven met de 3d + tijd dimensie, ipv de 10 dimensies van de snarentheorie met daarbij de 3d membramen die als eilanden door een multiversum klotsen waartussen grote gaten van hyperruimtes aanwezig zijn.
De brane theory is toch niet zo ver gezocht, als je blijft denken vanuit het paradigma van multiple universes en multiple dimensions? Het geeft gelijk een verklaring van het misterieuze ontbreken van de Ether (Michelson Morley experiment). De energie van 1 cc vacuüm, dat genoeg is om alle oceanen op Aarde te laten koken, laat zich immers niet verklaren zonder een onderliggend substraat.
quote:Ik heb (ook) bij 't Hooft gestudeerd. Ik ben wat sceptischer. Eerst dat Higgs-veld zien en dan maak ik de overstap.Op zondag 25 juli 2004 16:36 schreef Bard_Yttap het volgende:
[..]
Welke kant wil jij dan op? The brane theorie gaat verder dan de supersnaar theorie en blijft dus interessant zolang string theory in zwang blijft. Opmerkelijk is wel dat van 't Hooft er ook niets in ziet, terwijl hij wel aan de wieg van het nog niet gevonden Higgs boson heeft gestaan. Het toeval wil nu dat de Higgs boson de eerste kandidaat voor de graviton is. Wordt de Higgs boson dus ontdekt, misschien zodra the Large Hadron Collider (LHC) in april 2005 bij CERN gereed is, dan is dat full-circle voor String-theory en Brane-theory en bye bye van 't Hooft.
De brane theory is toch niet zo ver gezocht, als je blijft denken vanuit het paradigma van multiple universes en multiple dimensions? Het geeft gelijk een verklaring van het misterieuze ontbreken van de Ether (Michelson Morley experiment). De energie van 1 cc vacuüm, dat genoeg is om alle oceanen op Aarde te laten koken, laat zich immers niet verklaren zonder een onderliggend substraat.
Het mooie van de ether theorie, of liever gezegd het ontbreken van de ether, is dat hij een revolutie in de natuurkunde teweeg bracht.
Met de Higgs veld theorie zal het hetzelfde zijn.Als het aantoonbaar niet bestaat (het zou equivalent moeten zijn met de ether) hebben we weer een revolutie in de natuurkunde. Echter als het Higgs deeltje gevonden wordt, ook.
Ik zou niet weten waarom de ether in de een of andere vorm behouden of opnieuw geïntroduceerd zou moeten worden. Ik snap waarschijnlijk niet wat je bedoelt.
quote:TIME, CLOCK ADJUSTMENTS AND THE RELATIVITY POSTULATES
In his Special (Restricted) Theory of Relativity of 1905, Albert
Einstein proposed two postulates which can be considered to be the
result of the seeming inability to detect the reference frame in which
travels. [A. Einstein, Ann. Phys. 17, 891 (1905). For an English
translation, see A. Einstein et al., "The Principle of Relativity,"
Dover Publications, New York, (1958)] They are re-phrased somewhat
differently here for special emphasis:
1) "As long as the reference frame in which light travels is not
detected, the laws of physics can be considered to be the same in every
inertial frame, thus making all such frames equivalent."
2a) "In order to be consistent with any non-detection of the light
frame, the one-way speed of light would have to be measured in all
inertial coordinate systems to be equal to to the same constant, c , as
the average round trip speed of light. To insure this result, we must
use the Einsteinian-Lorenzian method of synchronizing clocks in a
relative manner. I.e., the time which is set on a "distant" clock is
arrived at by assigning a value of c (whether it really is or not) as
the unmeasured speed of light traveling from one clock to another and
assuming that the second clock should indicate the time when the light
signal left the first clock plus the time increment, delta t= d/c ,
where d is the distance between the clocks. Clocks which are coordinated
in this manner are said to be operating on a local, non-absolute system
of relative time which varies from frame to frame."
2b) "Since the speed of light is always measured to be equal to c,
it must be independent of the motion of the source."
[This source independence of light speed is consistent with
experiment and with ether theory, thus excluding Newton's ballistic
(source-dependent) theory of light and any other proposal to explain
light propagation.]
It can be shown that the "reverse" one-way speed of light
(i.e.,measured in the direction opposite to the direction of the
Einsteinian light signal used to set the second clock) can be equal to c
only if length contraction and time dilation really occur in an absolute
sense in the observer's frame.
Since no one knew how to set separated clocks (because the one-way
speed of light was unknown) so that the absolute light frame could be
detected, Einstein decided to advocate his particular type of time,
which, unlike real time, requires the re-setting of clocks every time
the observer changes from one frame to another, which for an observer on
the earth would be constantly. The only possible reason why clocks would
require re-setting on changing frames is that the real unmeasured speed
of light changes. Thus two frames in relative motion which are totally
equivalent in every other way will have clock systems which are
different.(i.e., the Lorentzian time-phase factors are always different
and the clock rates are almost always different), resulting in the
observers measuring different values, respectively, for a given length
or mass of nearly all objects and different rates for nearly all clocks,
regardless of the state of motion of whatever is being measured.
An observer in a state of absolute motion will measure the one-way
speed of light to be isotropically equal to c only when using
Einsteinian time. When at absolute rest, it makes no difference how
separated clocks are set because the real one-way speed of light, c ,
becomes identical to the Einsteinian one-light speed, c , and the
relativity theory and our Light Frame (ether) Theory will then yield
completely identical results.
Although the speed of light originating from a moving origin and
observed to be traveling along the y' axis perpendicularly to the
absolute ditection of an observer moving at an absolute speed, v , turns
out to be equal to c/g in absolute units, where the relativistic scaling
factor, g , or gamma, is equal to
1 / (1 - v v / cc)^1/2 ,the moving observer will still measure its
speed perpendicularly to the x' axis to be equal to c , since his clocks
all run at the slower absolute rate of t/g , where t is absolute time,
according to our Light Frame Theory. The real perpendicular velocity
component of any light signal will also still be equal to c , regardless
of the value of the x' component and the method used to synchronize
clocks.
Since no measuring rod contraction occurs perpendiculatly to the
(x') direction of absolute motion, all observers, whether at absolute
rest or moving parallel to the x' axis, will measure any prpendicular
distance, e.g., y , y' , or s, to have the same real value. (Ignoring
any absolute direction of different frames, the frame invariant, s ,
occurring in the expression,
ss=cctt-xx-yy-zz , can be a real or illusory measured perpendicular
physical distance when the axes are oriented so that at least one
spatial dimension can be dropped, therby eliminating the need for
imaginary numbers and space-time.
It is often acknowledged by the proponents of relativity that
lengths and clocks must somehow really be different in different
inertial frames, in order to account for the fact that different
observers measure the same constant, c , for the round trip light speed,
but they never follow through on this assumption and show in
quantitative terms that they are indeed correct. Their assumptions
become even more reasonable when we realize that many different inertial
observers will measure different values, respectively, for the length of
our own measuring rods, the rate (tempo) of our clocks, and the values
of masses at rest in our frame. Also, the only way that an observer in
constant uniform motion can measure the (unreflected) one-way speed of
light as he approaches a light source to be the same as when he recedes
from the source is for his clocks to be out of true synchronization by
virtue of having been set by Einstein's clock setting convention. This
will artificially reduce the measured light speed when approaching the
source and increase the measured value when receding, both by just the
right amount.
If Einsteinian time must be used to insure that the measured
reverse one-way speed of light is equal to c , then one may wonder why
the measured real average round trip speed of light is also equal to c
in different inertial frames, where only one clock is used in a given
frame to make the measurement. The reason is that such measurements
involve the average value of generally different light speeds, normally
involving a real speed greater than c in one direction and less than c
in the opposite direction, thereby giving us a true determination of
reality relative to the observer, which has nothing to do with relative
time, relative clock synchronization, relative simultaneity, the
equivalence of frames, or even the Lorentz transformations, which deal
with only one-way light speed measurements. Even though the real one-way
speed of light may be higher in the same direction in another frame, it
will be lower in the opposite ditection by just the right amount to
retain an average round trip speed of c.
[ A.J. Brown, "A New Test for the Anisotropy of Space," to be
published.]
Moreover, when clocks have been set by Einstein's method, an ad hoc
clock-rate measurement method must be imposed (which is unnecessary when
clocks are in true synchronization) which requires the use of two clocks
in one's own frame and one clock in the other frame, when measuring the
rate of a moving clock. Thus relativity prohibits an observer from using
one of his clocks to compare the time rate of a succession of moving
clocks in another frame as they move by. This reverse procedure,
however, does tell how the other observer would compare clock rates
between the two frames when following the synchronization convention of
relativity.
When using relative local time, since the measured one-way speed of
light must, in general, differ from what one would measure if clocks
were in true synchronization, likewise all other measured velocities
would also have to differ when using Einsteinian-set clocks. Thus, e.g.,
what either frame measures for the speed of the other frame would
normally be different if each were to use truly synchronized clocks.
It should be mentioned that, except for a small untested anomally
which would be measured only by observers in absolute motion,
[ A.J. Brown, "A New Test for the Anisotropy of Space," to be
published.]
there is no conflict between the different, but compatible, sets of
equations derived according to these different definitions of time. In
fact, several other definitions of time could be used, such as absolute
time and also the time which results when clocks in one frame are
coordinated so that they are out of true synchronization to the same
degree as those in another frame. The latter could be done in different
ways, e.g., after setting their clocks to relative time, the clocks in
both frames could be changed by identical amounts until both observers
make mutually reciprocal and non-paradoxical measurements, rather than
the Einsteinian "A>B>A" or "B>A>B" type of measurements for a given
quantity, although there is an even chance that they will be
qualitatively wrong. But only with truly synchronized clocks will an
observer find the real comparative values for all measurements relative
to him, and all such inertial observers will then agree on either an A>B
or B>A reciprocal relationship for a given quantity measured between
frames. Moreover, measurements made from two different frames, of
quantities involving a third frame, would also be logical, rather than
paradoxical.
If the degree to which relativistic effects occur is a function of
one's absolute velocity, then different frames are generally not totally
equivalent and some laws of physics would be slightly different, e.g.,
the anisotropy of the real one-way speed of light would violate
Einstein's FIRST postulate. Indeed the results of different types of
recent experiments indicate that the real one-way speed of light
generally is not equal to c.
[D.J. Torr and P. Kolen, "An Experiment to Measure the Relative
Variations in the One-Way Velocity of Light, U.S. Natl. Bur. Stand.,
Spec. Publ. 617, 1984.
E.W. Silvertooth, Nature 322, 590 (1986).
E.W, Silvertooth, "Experimental Detection of Anisotropy in the
wavelength of Light," to be published.
E.W. Silvertooth and S.F. Jacobs, Appl. Opt. 22, 1274 (1983).]
This does not violate the second postulate because, as far as one-way
light speed is concerned, this postulate applies only to measurements
made when assuming that the speed of light in one direction is already
equal to c.
Even though Einstein simply ignored the ether as superfluous
(redundant, extraneous and unnecessary - [but compatible]), we can start
with the ether concept as a single master postulate and, when using his
definition of local time, we can derive the Lorentz transformations as
well as the relativity postulates (by temporarily ignoring absolutes)
which would then follow from the Lorentz transformations. If one's
measuring rods really contract and clocks really run slower, both by a
factor of g [gamma], for an absolutely moving observer, then ALL
measured velocities parallel to the absolute direction of motion would
be equal to
v'=gg(v-vsubB), where vsubB is the absolute velocity of moving observer
B and v is any other parallel velocity or component measured by absolute
observer A. However, when v and vsubB do not appear in the same
equation, v will normally represent vsubB, such as in the corresponding
expression for one-way light measurements, c'=gg(c-v) . From this
equation, it can easily be shown that the round trip speed of light in
any direction must be equal to c for all observers in absolute motion.
[A.J. Brown, "A New Test for the Anisotropy of Space," to be published.]
Our ether theory is compatible not just with the Michelson-Morley
experiment [A.A. Michelson, Am. J. Sci., 122, 120 (1881); A.A. Michelson
and E.W. Morley, Am. J. Sci., 34, 333 (1887); Phil. Mag., 24, 449
(1887).] and its required absolute length contraction, but with the
Kennedy-Thorndike expriment as well, where it was shown that absolute
time dilation must also occur [when the arms of the interferometer are
of unequal lengths] if the ether is to exist. [R.J. Kennedy and E.M.
Thorndike, Phys. Rev., 42, 400 (1932).]
It is not unreasonable for an absolute contraction to occur. E.g.,
if the etheric waves composing a subatomic particle were to exist in a
pattern of waves traveling in a closed loop when the particle is at rest
in the ether and if the absolute amplitude of the perpendicular
component of each wave remains the same when the particle is moving
linearly through the ether, then we should be able to predict the new
dimension of the particle, or wave path, in the parallel direction by
taking the ratio of the absolute round trip speed of the wave in the
parallel direction to the absolute speed of the wave in the
perpendicular direction, since the distance covered by the component of
the wave in each direction must be such that the period of time required
for a round trip in each respective direction is the same. Otherwise
each individual part of each wave would have to be in more than one
place at the same time. Since the absolute round trip speed of
electromagnetic waves relative to a moving frame as seen by an absolute
observer is c/g in the perpendicular direction and c / gg in the
parallel direction, the ratio of the two speeds is c/g / c/gg=g and the
ratio of the time periods of each component covering a given distance is
1/g. Thus in order for the time periods to be equal, the parallel path
distance must be reduced to 1/g of the perpendicular path distance,
causing a contraction which leaves 1/g of the parallel dimension of all
particles, and consequently of all atoms by virtue of cohesive forces
and finally all larger objects, being held together cohesively. When
traveling at virtually the speed of light, the atoms and subatomic
particles would be virtually flat, since the etheric waves, traveling at
the speed of light, would be unable to make more than infinitesimal
parallel progress beyond the center of mass of any particle, because the
particle itself would be traveling at a speed of virtually c. Efforts to
measure the Lorentz contraction may fail unless one realizes that the
contraction is caused by physical forces -- which can be opposed by
other forces -- and is not necessarily the automatic magical result of
an equation. E.g., when using a rotating disc to measure any decrease in
the separation of high speed atoms, one must realize that atoms located
at the same radius from the center of the disc cannot come closer
together without pulling other atoms farther apart, even if the
subatomic particles contract. Thus the disc must not be continuously
solid. It could, however, somewhat resemble a spoked wheel with the hub
comprising most of the wheel and having a discontinuous outer perimeter,
with each outside section connected to its own short "spoke," thereby
allowing contraction to occur.
Moreover mass must increase with absolute velocity because of the
ether barrier. Since a physical particle (or object) can not exceed the
speed of the etheric waves which compose it, when it is traveling at
nearly the speed of light w.r.t. the ether, an amount of kinetic energy
which attempts to impart an additional velocity to it is transformed
mostly into mass and kinetic energy of the particle, but virtually no
more velocity.
The only important difference in Hendrik Lorentz' and Einstein's
theories is the fact that Einstein ignored the very physical conditions
(the ether and its consequences) which mandated the transformations,
while Lorentz relied on the ether concept and just one postulate -- the
apparent inability to detect the motion of objects w.r.t. the ether
(which Einstein split into two postulates). While Lorentz (and Einstein,
for that matter) never found the causative missing link -- the
consequences of the wave nature of sub-atomic particles in the ether --
which could have physically explained length contraction etc.,
Einstein's theory was more deficient in that it totally ignored all
possible explanations of relativistic effects and the relativity
postulates, thereby unnecessarily relegating relativity to a black box
theoty of measurements. The reason why relativity has been so hard to
truly understand is that no physical explanation or hypothesis was ever
offered which is compatible with Einstein's statement that the ether is
not needed. An aspect of physical reality which is not directly
observable (even if deductive logic demands it) does not necessarily
cease to exist simply by our ignoring it. There must be an
understandable physical reality which makes Einstein's postulates appear
to be true when absolutes are ignored, but Einstein chose to leave these
mandatory mechanisms and the causes underlying relativity to others to
discover.
To say that absolutely synchronized time does not exist is
equivalent to declaring that it is physically impossible for working
clocks in different locations in the same frame to read the same time.
This hypothesis has not only never been proven, but no physical
explanation has ever been offered which might explain why it is
permissible for one clock to be ahead or behind another clock but can
never read the same time even by accident or by gradually changing the
reading on one clock to cover all possible values corresponding to every
real one-way light speed which could have been used to set the separated
clocks. These light speed values would have to be higher than a real
relative speed of c/2 in one direction but could approach infinity in
the opposite direction (as the observer approaches the speed of light),
in keeping with the requirement that the average speed of light in free
space is equal to the constant, c .
If thre is any problem in truly synchronizing clocks, it is a
practical problem (which may have already been solved), not a profound
philosophical or metaphysical problem. The past difficulty with
absolutely synchronized time has never been that it can not exist, but
in not knowing when one has it. If clocks in different places are not
permitted by relativity to read the same real time, then how close are
their readings allowed to become? Can they be infinitesimally close for
an observer so that they cannot be distinguished from absolute
synchronization? Moreover, which Einsteinian-set clock would be ahead of
the other and by how much and why?
The slow clock-transport method is a perfectly valid procedure to
set separated clocks, when properly used. However, the method is often
misinterpreted as requiring the measurement of the velocity of the
moving clock during transport in order to take time dilation into
account. But this interpretation is invalid because it turns out to be
equivalent to Einstein's relative method of clock setting. It can be
shown that if a clock can be moved slowly enough and no correction is
made for time dilation, the discrepancy between the original clock
reading and the transported-clock reading can be made so infinitesimal
that, for all intents and purposes, the clocks can be considered as
absolutely synchronized.
According to relativity, two separated clocks in one reference
frame will differ in synchronization from two clocks similarly oriented
and the same local distance apart in a different inertial reference
frame, when synchronized by Einstein's method. The result of Einstein's
procedure is the anti-reciprocal A>B>A or B>A>B type of paradox for
mutual length, mass and clock rate measurements. The difference in
readings of a pair of clocks in one frame will be either greater or less
than the difference, if any, in the other frame. We must now ask 1)
WHICH frame has the greater difference in clock readings, 2) what is the
exact degree of the difference, and 3) why? Since relativity ignores the
ether, it has no answers. But Einstein's equations ironically describe
the ether and demand the non-equivalence of different reference frames,
thereby making the theory internally inconsistent, notwithstanding his
efforts to force the unmeasured one-way sped of light to be equal to c.
Einstein's clock setting method is what forces inherently different
frames superficially to appear to be equivalent, but when a pair of
clocks changes frames and are not re-set, a light signal from one clock
to the other will generally arrive either sooner or later. This means
that the physical situation in one frame is not the same as the physical
situation in another frame as far as similarly oriented light signals
are concerned. Only the ether concept enables us to understand why there
is a difference and why the frames are generally not equivalent in every
way. Although a one-way light signal must arrive late if we accelerate
(in the same direction as the light is moving) to a new inertial frame,
relativity can not predict how late the signal will arrive or how early
(in case we accelerate in the opposite direction). Only our ether (light
frame) theory can give us a quantitative answer.
1997 note: There will be some difficulty in reproducing some of the
following equations for the internet because in the original printed
article, boldface was used to denote illusory quantities and many
subscripts were used. I will now use upper case letters to denote
illusory quantities and if the original notation indicated
t'sub(x'=0), I will change it to read t'@x'=0. (Of course I did not use
the word "sub" in the original paper. I used the actual subscript.) When
writing the original paper in long hand, I simply drew a circle around
an illusory quantity so it would't be confused with the corresponding
real quantity. - AJB
DERIVATIONS.
The Lorentz transformations, which are designed to give the
relationships between measurements made by different observers in
uniform relative motion, were first discovered by Woldemar Voigt in
1887 in an investigation founded on the elastic theory of light, but are
generally attributed to Lorentz, [H.A. Lorentz, Proc. Acad. Sci.
(Amsterdam), 6, 809 (1904).], who independently had them published in
1904 after Joseph Larmor [J. Larmor, Aether and Matter, (Cambridge
University Press, 1900).] in 1900. Henri Poincare arrived at similar
results in 1905.
Lorentz was well aware that for absolutely moving observers, his
tranformations (with their local time) generally did not give the real
physical values for measurements of moving bodies, but were considered
by him as mathematical aids to calculation. E.g., it can be shown that
while such measured values of velocity and measurements of masses in
motion are not normally real, their product will give real momentum.
[A.J. Brown, "A New Test for the Anisotropy of Space," to be published.]
Similarly, the product of an Einsteinian illusory velocity and an
Einsteinian illusory time interval gives a real stationary distance in
the observer's frame.
The measurements predicted by special relativity can best be
understood when one coordinate system is at rest in the ether, which
creates real relativistic effects in the moving system, with no real
relativistic effects occurring in the stationary frame. When this
approach is taken, we can not only calculate what each observer will
measure, but the reasons for obtaining each particular value of whatever
is measured is completely understood by also calculating real lengths of
measuring rods and real clock rates,etc. When this is done, relativity
ceases to be magical and becomes understandable.
The Lorentz transformations are based on a diagram depicting the
relative motion of two different reference frames, A and B, where light
signals are emitted in all directions from their origins when the
origins coincide at time t=t'=0. Measurements made from the stationary
frame,A, are indicated by unprimed symbols and measurements made by
Frame B, moving to the right, are indicated by primed symbols. If we
want both observers to measure c for the unknown [one-way] speed of
light, we must write x=ct and x'=ct' and set the clocks by assuming that
c'=c. Thus c=x/t=x'/t' , or t'=x't/x , i.e., at the same instant in
absolutely synchronized time, the value of the time in one frame would
normally be different from the time value in the other frame. This means
that the equations x'=x-vt and x=x'-v't' from classical physics will not
balance, except when t=t'=0. In other words, the absolute distance from
either origin to the position of the light signal will be measured by A
to be different from the same absolute distance as measured by B.
In relativity the ratio of the distance measured by an observer
from his own origin extending to the position of such a light signal to
the same "absolute" distance as measured by the other observer is
defined as g, gamma, where g=x'/(x-vt)=x/(x'-v't'), when clocks in
different locations are set by light signals of unknown velocity.
Rewriting the above will give us the Lorentz distance transformations in
their conventional form:
x'=g(x-vt) (1)
and x=g(x'-v't') (2)
Thus light will cover a different distance in different frames
during the same "absolute" time interval, since x' is not equal to x
(except at t=t'=0).
In order to obtain the Lorentz time transformations, we divide
these equations by c:
x'/c=g(x/c -vt/c) , t'=g(t -vx/cc) (3)
and x/c=g(x'/c -v't'/c) , t=g(t' -v'x'/cc) (4)
Thus we have forced the one-way measured speed of light in each frame to
be equal to c, whether it would be or not if all clocks were truly
synchronized. We will show later that v=-v', but for now we will simply
assume it to be true, as Einstein did.
Since the time throughout the the B frame wil be found to vary with
the value of x', at any given time, t', at B's origin, we will
distinguish from t' by circling it in longhand, (t') , which we might
call "t' circle," or by putting it in boldface type or underlining it
when typing or printing. [1997 note: I'll use caps for these postings -
in my paper I used boldface] Since this unconventional Einsteinian, or
Lorentzian, time is generally not the true time in the B frame, we will
call it "illusory" time and let the time, t' , at the origin be called
"real" time. When necessary to avoid confusion when talking about
illusory time, we must specify the location of the clock on the x' axis
(or the x' component of its position). Thus we would write T'@x'/c
[T'subx'/c] or perhaps just T'@x' to indicate the illusory time at the
position of a light signal and T'@x=0 to indicate the illusory time of
the B clock located at the A origin. The time, t'@x'=0, on the B clock
at the B origin is real (it was truly synchronized with the A clock at
the A origin) and can be written as t'. If both frames are in absolute
motion, we should use boldface type [caps] for all time values in both
frames where the clocks do not lie on the respctive y-z or y'-z' planes.
Since Lorentzian time is not the same as true time, it can not
always be used in the same way as true time since, unlike true time, it
is space-dependent, e.g., the farther the absolutely moving Lorentzian
clock is from the y'-z' plane, the more its reading will differ from the
clock reading at the B origin. Thus when measuring how long it takes
something to travel from one position on the x' axis to another
position, we must record the reading on each clock when the object (or
light signal) is adjacent to each respective clock. No problem arises
when the clocks are truly synchronized, even if the distance between two
moving objects and/or light signals is to be measured, but when
Lorentzian clocks are used, the method used in attempting to determine
the "simultaneous" location and corresponding time of two moving things
is critical, inasmuch as we must use different clock readings at the
same real, or "absolute," instant in time corresponding to the different
locations of moving points.
One error made by Einstein was that he ignored any
location-dependence of time within the OBSERVER'S own frame, e.g., at
the position of the origin of the other frame. This error is responsible
for the predicted disagreement between observers as to the ratio of
their clock rates and the ratio of the lengths of each other's measuring
rods, etc. When absolute time is used, no problem arises. Even when
clocks in different frames are out of synchronization to the same
degree, no contradictions arise. But if the actual simultaneous
Lorentzian clock readings at the positions of the two points, each in
relative motion w.r.t. the moving observer, are not used, tremendous
difficulties arise. In fact, except for the unlikely situation where one
frame is at rest in he ether, none of the Lorentz transformations will
balance in a manner showing REAL relationships when the Lorentzian time
is assumed to be the same in different locations in the same frame at
the same instant in absolute time. When the actual instantaneous
Lorentzian clock reading corresponding to its actual location is used
for each moving point, both observers will agree on the true
relationship between their respective unit rod lengths (which would be
identical when there is no relative motion between the two frames), and
the transformations will balance, but with g (a function of the absolute
speeds of A and B) inverted in equation (2). However, this involves the
determination and application of some kind of meaningful simultaneity.
Velocities calculated with illusory time and a real distance (as is
normally the case in relativity) are also illusory and will be
symbolized, e.g., as V' , when measured from the moving frame. In the
Lorentz transformations, the assumed one-way speed of light , c , is
almost always illusory in the moving frame and thus is seldom really
equal to c in a real life situation unless traveling perpendicularly to
the direction of the moving frame and, strictly speaking, should be
designated in boldface [caps] as C' (or C in the unprimed frame if that
frame is also moving w.r.t. the ether). However, for convenience we will
not use boldface type [caps] or the prime symbol when it comes to
illusory light speed, since the illusory value of light speed is always
set equal to c by Einsteinian convention.
In order to derive a convenient formula for g as a function of c
and v, or -V' , we will use boldface type [caps] for the illusory time
in the B frame and re-write equations (1) and (2) as
cT'=g(ct-vt)=gt(c-v) and ct=g(cT'+vT')=gT'(c+v), respectively. Solving
each equation for t/T' and equating gives c/[g(c-v)]=g(c+v)/c ,
gg=cc/(c-v)(c=v) , gg=cc/(cc-vv)=1/(1- vv/cc) , or g=1/ (1 -vv/cc)^1/2 =
1/ (1 -V'V'/cc)^1/2. When A is also in absolute motion and the distance
between origins is being compared, the equation becomes v't'=V'T'@x=0 =
(-gsubB/gsubA)VT@x'=0 , where gsubB and gsubA pertain to the respective
gammas between a given moving frame and the absolute frame. Since, in
this case, we will let g=gsubB/gsubA and V'=-V , we have T'@x=0 =
gT@x'=0. The time, T@x'=0 , and V are in boldface type [caps] to cover
the general case where the unprimed frame may have an absolute velocity.
Setting x=0 in equation (3), in the case where both frames are in
absolute motion in any direction and when the illusory factor, G ,
calculated from V or V' is used, we have T'@x=0 = Gt@x=0 , and from
equation (4), we have T@x'=0 = Gt'@x'=0 , which qualitatively (not
quantitatively) gives the relationship between clock rates. We also have
T'@x=0 = Ggt'@x'=0 , since t@x=0 = gt'@x'=0 , where g=gsubB/gsubA is the
absolute ratio of real clock rates. Thus the real ratio, g , of the true
clock rates of different frames can not be calculated from the
Einsteinian illusory velocity between frames. The observers must
calculate the true g, which is equal to t / t' . Under Einstein's rules
they won't know who is preferred because such rules do not permit the
determination of how fast a clock is REALLY running compared with one's
own. Only contradictory comparisons are allowed between frames in
relativity, generally. When real time is used in both frames, all
observers in both frames will find that t=gt' , where g=gsubB/gsubA ,
regardless of how comparisons are made. Thus frames A and B are never
fundamentally equivalent when they have different speeds relative to the
ether. When measurements follow the Einsteinian guidelines, it is true
that we cannot tell whether A or B is the preferred (slower moving or
stationay) frame. But to equate any inability to decide which frame is
preferred with the equivalence of the frames is a logical atrocity. It's
like saying that both sides of a lost coin are identical if you don't
know which side is up. When properly understood, the Lorentz
transformations almost always show us that one frame MUST be preferred
if they are to balance.
After the same interval of absolute time, B will find that what he
calculates for the distance between origins can take on an infinite
number of values, depending on the reading of the clock located at any
one of the infinite number of y'-z' planes that the light signal has
reached, depending on which direction it is traveling in three
dimensions. If B ignores the light (unless it is located on the y'-z'
plane containing A's origin) and concerns himself only with the position
of A's origin, he will find the correct value, relative to his frame,
for the distance between origins. I.e., the value is V'T'@x=0 , not
V'T'@x'/c , where -c't' <= x' <= c't' , which gives an infinite number
of distances between origins, at real tme t'@x'=0, ranging from
V'T'@x'=0 to V'T'@x'=-c't' and also to V'T'@x'=+c'T'. When the light
goes to the right, we have | V'T'@x' | < | VT@x' | and when it goes to
he left, we have | V'T'@x' | > | VT@x' | , where | V'T'@(to the right) |
/ | V"T'@x'(to the left) | = (c-v) / (c+v). When real time is used, no
such nonsense is possible.
According to the Lorentz transformations, if A at true rest
calculates (in his units) the correct distance, vt , between origins,
what should B calculate for the same distance between origins for the
same moment in absolute time where t=gt' ? If he uses his own units,
there is no way that B can measure or calculate the distance between
origins to be the same as what A finds at the same instant, and it makes
no difference whether A or B is moving slower or is stationary in the
ether. This is easier to see if B uses illusory measurements. If the two
distances were equal, since v=-V' , the illusory time interval in the B
frame would have to be equal to A's time interval, i.e., vt=-V'T'@x=0
and thus t=T'@x=0. Since T'@x=0 = gt, it is clearly imposssible to have
T'@x=0 = t unless g=1, which would mean that frames A and B would have
to be equivalent, which in turn would violate the special relativity
requirement that g=1 / (1 -vv/cc)^1/2 > 1 for frames in relative motion.
If the position of A's origin corresponding to time, t , is known to B,
then B could also use measuring rods to determine the distance between
origins, rather than by using the V'T'@x=0 method.
The equation, delta x'=g(delta x), holds for ANY real comparison of
lengths or distances parallel to the x and x' axes, even if one end
point of the length being measured is traveling in a third frame and the
other end point is traveling in a fourth frame -- and if one or both
points are light signals. Unreality in physics is like fibbing in life
-- you have to remember your indiscretion -- in this case how you made
your measurements. When real measuremnts are made, it makes no
difference how it is done, and the measurements made from ONE of the
frames will almost always be numerically higher (or lower) than
measurements made from the other frame for given locations of whatever
is being measured and the type of quanity (lengh, mass, time, velocity
etc.). E.g., in the case of real rod length measurements, r and r', we
would always have r'/r=gsubB / gsubA when the rods are parallel to the
direction of absolute motion. It makes no difference if the rod is in
Frame A, Frame B or an entirely different Frame C. When Einstein's
illusory measurements are used, A and B will disagree on which rod is
longer, even if the rod is half way between the A and B origins (unless
the rod is at rest in the ether, in which case frames A and B would be
equivalent [in this example]).
Even though the resl position of a single point can be correctly
calculated by the product of the illusory velocity and illusory time,
the real x'-component distance between two points BOTH MOVING at the
same or at different velocities (parallel w.r.t. a moving observer)
cannot in general be correctly calculated with illusory quantities,
using Einstein's method. This is why B's illusory calculation of the
length of a rod at rest in absolute Frame A is lower than the real
relative length by a factor of gg. It makes no difference whether B
calculates the illusory length from the illusory velocity and the real
time that it takes the rod to pass a point in the B frame, or if he
determines the apparent location of each end of the rod at the same
apparent illsory time, although the time at one end can be real.
From a frame moving w.r.t. the ether, all velocity measurements not
parallel to the y'-z' plane become illusory, as well as all time
intervals used for measuring change of position. In spite of all this,
all measured and calculated distances will be real -- as long as the
Lorentzian time corresponding to the actual position of the moving point
is always used. In the traditional Lorentz tranformations, the distance
measured by Observer B between origins is always incorrect, unless the
light at x' is located on the y'-z' (x=0) plane of the observer moving
through the ether perpendicularly to that plane or whenever the observer
is at rest in the ether, because the Lorentzian time at the position of
the light is used, rather than the Lorentzian time at the position of
the moving origin.
From the equation relating real time in different frames, we can
substitute illusory quantities in the following way by writing
deltaT=gsubB/gsubA deltaT', where T and T' pertain to all stationary
clocks in their respective frames, since the RATE at which ANY
stationary clock (real or illusory) in a frame runs is independent of
its location. At the origin of the B frame,we have deltaT=gsubB/gsubA
delta t'. [Time is real at B's origin.] If t=t'=0 when the origins
coincide (say A now is at true rest), we have t/g=t'. Inserting this
into Equation (4) gives t'=T'+(vx'x'/cc), which shows the relationship
between real time and illusory time anywhere in the moving B frame. We
can now convert from either system of time to the other system at will.
However, when operating under the limitations of special relativity,
there is only a 50% chance of guessing which frame is moving slower
w.r.t. the ether or is stationary. If we guess correctly and adjust the
clocks in one frame according to the correction factor Vx'/cc or Vx/cc,
as the case may be, then the clocks in both frames will be out of
synchronization to the same degre, and both observers will agree on the
reciprocal relationships and be either quantitatively or merely
qualitatively correct, depending on whether one frame is at true rest or
not (V is in boldface type [caps] in case A is moving). If we guess
incorrectly and pick the wrong frame as the preferred frame, then both
observers will still agree on everything but will be incorrect about
everything, i.e., whose clocks run faster, etc. In either case, only one
observer will find that the faster the other frame moves, the lighter
its masses become, etc., and thus the frames would not be equivalent.
There is no conflict as such between different systems of time. It
is only a matter of convenience combined with a true understanding of
what a given system means.
We can also set the synchronization of clocks in one frame to agee
with the synchronization of clocks in another frame by setting the
clocks by Einstein's method in each frame when there is no relative
motion between them and then have at least one frame accelerate to a new
inertial frame, thereby eliminating all contradictory measurements
(although measurements from the new frame(s) will quantitatively vary
from relativity).
Since x'/T'=c and T' is not equal to t' (except at B's origin), we
have x'/ t' is not equal to c. Therefore this equation can be re-written
as x'/t'=c' , where c' is not equal to c. Thus x'=c't'=cT' , or
t'/T'=c/c' . Even if x'/ t' is not equal to c for a moving frame, we can
substitute the variable location-dependent local time, T'=x'/c , or
T'=t' c'/c, so that no matter by what factor the actual speed of light
differs from c, we can multiply the real time by the same factor, c'/c ,
so that one can then claim that the unidirectional speed of light is
also a universal constant! The effect of Einstein's
pseudo-synchronization of clocks in a frame moving to the right is to
multiply the real relative light speed by a factor of 1 + v / |c| when
it is also traveling to the right and by a factor of
1 - v / |c| when it is traveling to the left.
The two expressions for T' can be equated a follows:
T'=t' c'/c = t' -vx'/cc = t' -vc't'/cc. Re-writing gives c'/c =1
-vc'/cc, and c'c = cc-vc' , and c'(c+v) = cc, and c' = cc/(c+v). Since
cc/(c+v)==gg(c-v), we obtain c'=gg(c-v). [1997 note: This is my favorite
equation. AJB.] Thus we see that the true parallel one way light
velocity is greater ["different" might be a better word - watch your
signs - the earth's velocity will be positive in one direction and
negative in the other, if we want to keep c' and c positive] than the
predicted classical light velocity by a factor of gg. This is to be
expected since delta x'=g delta(x-vt) and delta t'=delta t'/g, so that
the general expression for all real parallel balistic velocities
measured from the moving frame is u'=delta x'/delta t' =
g delta(ut-vt)/(delta t/g) = gg(delta t)(u-v) / delta t = gg(u-v) =u',
which is consistent with the non-ballistic equation, c'=gg(c-v). [1997
note: Again, I really LOVE this equation. It's a real sweetheart! It's
the formula for the real unidirectional speed of light in any frame
moving relatively to the structured properties of space. The RT speed of
light, the universal constant, c, is simply the average of the go and
return legs of the light path. In general, light speed is greater than c
in one direction and less that c in the opposite direction. The degree
of the difference depends on how large the value of the component of the
light velocity is in the direction of the earth's motion. When that
component is zero (earth & light moving at right angles), c'=c. When
earth and light move parallel to each other, the difference is the
greatest and the absolute veocity of the earth can be determined. AJB]
We can also find the difference between true time, t' , and
illusory time, T' , without using the time in the stationary frame or
the equation, t=gt' , if we use the relationship T'/ t' =c'/c. This
gives us t'-T'=t' -t'c'/c = t'(1 -c'/c) = (x'/c')(1 -c'/c) = x' { [ 1/
gg(c-v) ] -1/c}. Since gg==cc/(c-v)(c+v), we have t'-T'=x'[(c+v)/cc -
c/cc]. [ Note: == means "identically equal to" ] Thus again
t'-T'=vx'/cc, where x' can represent anything, not just light signals.
However, when written as t'-T'=v/c T' or t'=T'(1 +v/c), T' must
represent the illusory time at the light signal. Although some
physicists regard the vx'/cc, or vT'/c , factor as unexpected, [R.P.
Feynman. R.B. Leighton, and M. Sands, "The Feynman Lectures in physics,"
(Addison-Wesley, Reading, Mass., 1963), p. 16-2.] it can be thought of
as a kind of counterpart of the term, vt/c, which arises under classical
ether conditions where relativistic distances, time intervals and
velocities are ignored. Thus if we use Equation (1) in its classical
form, x'=x-vt, (since g=1), and have the moving observer B insist that
the one-way speed of light is c rather than c-v, i.e., x'=cT', we can
divide by c and obtain the equation, x'/c=x/c -vt/c, where x'/c=T' and
x/c=t, or T'=t -vt/c = t -vx/cc. The term, vx/cc, is the real time
(t=t') that it takes light to cover the distance vt=-v't' , while T' and
t are the time intervals that it takes the light to cover the distances
x' and x, respectively. Thus the term, vx/cc, arises because the moving
observer,B, must take into account the time for the light to cover the
distance vt=-v't'. When relativistic effects are considered, the term,
vx'/cc, arises for a similar reason, since Equation (2), x=g(x'+vT'),
can be written as x/g=x'+vT'. Dividing by c gives x/gc = x'/c +vT'/c, or
t/g=t'=T' +vx/cc.
The relationship between t' and t can also be found as follows:
t'=x'/c' , t'=g(x-vt) / [gg(c-v)], (A at true rest), = (ct-vt) /
[g(c-v)] = t(c-v) / [g(c-v)] =t/g, where all quantities are real. The
conventional way of attempting to derive this false equation, by setting
x=0 in Equation (3), T'=g(t -vx/cc), is mathematically invalid since T'
is not equal to t'. Thus it is impossible for the two frames to be
equivalent under these conditions, since a clock always runs faster in
the stationary (or slower moving) frame. Real quantities can never be
contradictory, ambiguous or nebulous and observers in both frames will
always agree on the inequalities such as delta t > delta t' , | delta x'
| > | delta x | and thus | v' | > | v |, when real parallel measurements
are made.
The relationship between B's illusory time at A's origin and B's
real time can also be found as follows: v't'=V'T'@x=0, T'@x=0 / t'
=v'/V' , v'=-(gsubBA)^2 v = T'@x=0 v'/ t' = GgsubBA, T'@x=0 =GgsubBA t'
, where the subscript, BA, denotes a measurement of B made by A. Also,
since t'= t/gsubBA , we have T'@x=0 = Gt.
The equal relationship between V' and -V can be verified from ether
theory as follows, rather that merely assuming it to be true on the
basis of Einstein's first postulate:
V'=Real distance / Illusory time =x'/ T' = v't'/T'@x=0 =
-gsub^2(vsubB-vsubA)t'/ (t' -vx'/cc) = -gsubB-vsubA)t' / [t'
-vsubB(v't')/cc] = -gsubB^2(vsubB-VsubA) /
{1+[vsubBgsubB^2(vsubB-vsubA)/cc]} = -(vsubB-vsubA)/ {(1/gsubB^2)
+[vsubB(vsubB-vsubA)/cc]} = (vsubA-vsubB) / {[(c-vsubB)(c+vsubB)/cc]+
[(vsubB^2-vsubAvsubB)/cc]} = (vsubA-vsubB) / {1-[vsubB^2/cc]+
[vsubB^2/cc]-[(vsubA-vsubB)/cc]} = (vsubA-vsubB) /
{1-[vsubA^2/cc]-[(vsubA-vsubB)/cc]} = (vsubA-VsubB) /
{[(c-vsubA)(c+vsubA)/cc]+ [(vsubA^2-vsubAvsubB)/cc]} = (vsubA-vsubB) /
{[1/gsubA^2]+[vsubA(vsubA-vsubB)/cc]} = gsubA^2(vsubA-vsubB) /
{1+[vsubA-vsubB)/cc]} = -v / [1-(vsubAv/cc)] = -vt / {t-[vsubA(vt)/cc]}
= -vt / [t-(subAx/cc)] = -x/t = -V. [1997 note: I hope I didn't go
around Robin's barn here. There's probably a shorter way to do this, but
since this worked, I left it alone.]
For A at true rest we can start with the equation t'=T' +vx/cc = T'
+vV'T'/cc and substitute T'@x=0 for T': t' = T'@x=0 +vV'T'@x=0 /cc =
T'@x=0 (1 -vv/cc) = T'@x=0 /gg , and T'@x=0 = ggt' . Since gg==1/ [1
-v/c)(1 +v/c)], we can write t'=x'/c' = cT'/gg(c-v) = T' /gg(1 -v/c) =
T'(1 +v/c) and t' = T' +(v/c)T'. Since t'=t/g, we have t/g = T'
+(v/c)T', and t=g [T' +(v/c)T'], and ct=g(cT'+vT') and x+g(x'+vT'),
which is Equation (2). From this equation we can derive Equation (1) as
follows: x=g(x'+vT'), ct=g(cT'+vT') = gT'(c+v) and t = gT'(1 +v/c).
Since gg==1 / [(1 -v/c)(1 +v'c)], we can write t=T'/ [g(1 -v/c)]. Thus
T'=gt(1 -v/c) = g(t -vt/c) , cT' = g(ct-vt) and x'=g(x-vt).
Dividing Equation (3) by Equation (4) in their new form gives us:
T'/ t = gt(1 -v/c) / gT'(1 +v/c) , T'T' / tt = (1 -v/c) / (1 +v/c) =
(c-v) / c+v), and T'/ t = [(c-v) /(c+v)]^1/2 , an equation from which
these four Lorentz transformations can be derived. Since x=ct and x'=cT'
, this equation can also be written in real quantities only (for A at
rest) as x'/x = [(c-v)(c+v)]^1/2 , which is also a pivotal equation from
which these Lorentz transformations can be derived with the help of the
identity, [(c-v)(c+v)]^1/2 == g(1 -v/c) == 1 / [g(1 +v/c)] , since gg=cc
/ [(c-v)(c+v)].
Dividing Equation (1) by x(=ct) also gives us the pivotal equation:
x'/x=g(x/x - vt/ct) = g(1 -v/c) = 1 / [g(1 +v/c)] , and (x'/x)^2 = g(1
-v/c) / [g(1 +v/c)] = (c-v) / (c+v), x'/x = [(c-v)(c+v)]^1/2 , or we
can simply write x'/x = c't'/ct = (c'/c) / 1/g = gg(c-v) / gc = g(1
-v/c) , x'/x = [(c-v) / (c+v)]^1/2. Also, since V'=-v, we can predict
the ratio of the respective measurements of the real distances between
origins by writing v't'/vt=V'T'@x=0 / vt = -T'@x=0 / t = -gsubB/gsubA =
-gsubBA.
Dividing Equation (1) by t gives us x'/ t= g(x/ t - vt/ t) ,
x'/gt'=g(c-v) , or c'=gg(c-v). The Lorentz transformations can be
derived from the real-time ether equations by first deriving Equation
(1) by multiplying the equation, c'=gg(c-v) , by t=gt' and then deiving
Equations (2), (3) and (4) from Equation (1).
For two reference frames in relative motion, it is mathematically
impossible to combine successfully equations (1) and (2) when Equation
(1) represents A at true rest and Equation (2) represents B at true
rest, because when a frame is at true rest, all time, velocity, and
distance measurements made in that frame are real, making the equations
mathematically contradictory, which, if a solution is forced, mandates
that both frames at least be at relative rest (w.r.t. each other), i.e.,
v=v'=0 or V=-V'=0.
An inherent imbalance exists which almost always favors one
specific frame over the other, and the equations per se cannot tell us
which frame is preferred until we learn to make actual measurements
which show what is happening at the same instant in absolute time in
each frame. As written, each of the Lorentz distance transformations
represents a relative situation where one frame is either at absoloute
rest in the light frame or both frames are moving in any direction at
the same speed or different speeds through the ether. When the two
speeds are different, the imbalance, or non-equivalence, can never be
removed.
Both equations, (1) and (2), include the distance betwen origins,
which is no problem in Equation (1) when everything is real, while in
Equation (2), we have seen that the distance between origins, VT'@x' ,
is permitted by relativity to be measured only by using the Einsteinian
time at the position of the light signal if Equation (2) is to be valid
-- and thus the distance between origins as measured by A is different
from the same absolute distance as measured by B at the same instant in
absolute time. However when the direction of the light signal is
reversed, the ratio of the respective measurements of the distance
between origins, V'T'@x' / VT@x = -T'@x' /T@x = -{[(-)c-v] /
[(-)c+v]}^1/2 , is inverted. Thus at the same instant in absolute time,
the "moving" observer will find two different incorrect illusory values
for the same real distance between origins. If B's clock reading is
taken at the position of A's origin, x=0, the distance between origins
will be measured to be V'T'@x=0 = -VT'@x=0. If B were to use truly
synchronized clocks, we would have v't'=-gsubBA vt, which is somewhat
similar to Equation (1).
When using the same illusory times to calculate the distance
between origins, the observer who measured the real distance between his
origin and the light to be smaller will also measure a shorter
(illusory) distance between the origins by the same exact ratio as with
the light distance calculation. Again, when the process is repeated with
the light traveling in the opposite direction, the observer's calculated
distance between origins (at the same instant in absolute time as
before) will also be changed, i.e., the ratio of the calculated
distances will be inverted and the observer who previously found the
shorter distance between origins will now find the longer distance,
which shows that such calculated distances must, in general, be
illusory. Although the distances between origins as determined by the
moving observer is generally incorrect regardless of the light
direction, averaging the two values would give the correct distance,
assuming that they can be found.
It is interesting that when A and B each determine the ratio of the
same two absolute distances, i.e., (B's origin to the light signal) /
(A's origin to the light signal), they will find (x -VT@x)/x = 1 -V/c
and x'/ (x' -V'T'@x') = 1 / (1 +V/c), respectively. In other words, when
Einstein's illusory quantities are used, A and B will not even agree on
the RATIO of the measured distances. The ratio of the ratios is (B's
ratio) / (A's ratio) = (1/ 1 +V/c) / (1 -V/c) =GG. Also, when one
observer says that two objects w.r.t. ANY frame are traveling at the
same speed in opposite directions, the other observer will almost always
disagree.
When two frames are not equivalent, the real relativistic effects
are more pronounced in one frame than the other, which causes the two
observers to arrive at different values when measuring the same absolute
distance, whether it be the distance between origins, the distance from
either origin to the position of a light signal, or the distance between
any other two points having different x components and different x'
components. E.g., when real time is used, we obtain (x'=v't') / x = g as
the ratio of measurements of the same absolute distance made by B and A.
When illusory time is used, x and x' remain the same but x'-v't' is
reduced by a factor of gg down to x'V'T'@x' , giving a ratio of
measurements made by B and A of (x'-V'T'@x') / x = 1/g. Although
illusory time can be injected into Equation (1) as x/c, and cT' can also
be substituted for x', such time plays no role in the measurement of x',
since the point x' is a given point which coincides with the point x and
thus is a completely agreed upon absolute position of the light signal.
In contrast, the point V'T'@x' is a total fantasy and has nothing to do
with even the LORENTZIAN time at A' s origin, let alone the real time.
A's origin is correctly determined by B if B's real time, t' ,is used in
conjunction with the real velocity, v' , or when the illusory time at
A's origin, T'@x=0 , is used with the illusory velocity, V'. When B
decides to use illusory time and measures distances with the velocity x
time method, it yields real distances except in Equation (2) where the
time at x' , which is to be multiplied by V' to give a distance, has
nothing to do with the illusory B clock located at A's origin. The ratio
of these two different illusory clock readings can be determined as
follows:
T'@x' / T'@x-0 = (x'/c) / (ggt') = (x'/c) / (ggt') = (x'/ t') / (ggc) =
c' /ggc = gg(c-v) / ggc) = 1 -v/c.
When the real distance, v't'=V'T'@x=0 , between origins is used,
Equation (2) becomes x=(1/g)(x'-v't') = (1/g)(x' -V'T'@x=0). The ratio
of the real measurement made by B to the Einsteinian measurement for the
distance from A's origin to the light signal is (gx) / (x/g) = gg. Thus
it makes a tremendous difference how B measures the distance between
origins, but A at true rest can use any method when his time is real and
thus does not depend on location.
When T'@x' is used, the Lorentz transformations approximate reality
when v/c is small, but if T'@x-0 can be used to find A's origin, i.e.,
V'T'@x=0 , the transformations will reflect reality, with the indicated
inversion of the real g in Equation (2).
Real local time in any frame can be observed compartively from any
other frame when the clocks in the observer's frame are truly
synchronized, i.e., when they all read the same throughout his frame
regardless of location. If the frame being measured is absolute, the
clock rates in that frame will be observed comparatively as absolute
time, the fastest time in the universe.
Any synchronized common universal time can be used in place of
absolute time. It does not necessarily have to be the time originating
in the absolute time frame. Even if absolute space did not exist (e.g.,
as would be the case with ballistic light propagation and no ether), an
agreed upon common universal time could still exist.
If we synchronize twin clocks while they are together in a truly
moving frame and then move them absolutely and in opposite directions at
th same ilusory speed and bring them to rest in their new locations, the
clock readings will not agree, i.e., one clock reading will be ahead of
the other. We now ask, "Can the discrepancy in the clock readings be
made smaller by accelerating our reference frame in a certain direction
and then transforming it into a new frame?" The answer has to be "yes"
because the synchronization of clocks varies from frame to frame. Of
course, we must choose the correct direction, otherwise the discrepancy
in clock readings will becone larger. (An exceptioin occurs when the
initial and final frames have the same speed relative to the ether.
What happens when two relatively stationary reference frames
proceed to move apart, one going in one direction and each coming to
rest again in new locations? Relativity would have to say that their
clocks would no longer have to truly agree, because if they did, then
truly synchronized time would have to exist, and that would contradict
the presumptions of relativity. But if the clocks disagree, the clock in
one frame would have to be ahead of the clock in the other frame, and
that would make one frame a preferred frame, which violates the first
postulate of special relativity. THEREFORE, REGARDLESS OF WHETHER THE
CLOCKS AGREE OR DISAGREE, SPECIAL RELATIVITY THEORY MUST BE
MODIFIED.
Ether theory resolves the dilemma by pointing out that when the clocks
move with the same speed w.r.t. the ether (regardless of direction),
they will still be synchronized, but when they do not move with the same
speed, they will not agree.
The real asymmetry of the tempo of oppositely directed clocks
moving w.r.t. one's own absolutely moving frame when their corresponding
Einsteinian speeds are equal is what generally prevents us from using
such clocks to absolutely synchronize our own stationary clocks. The
asymmetry can be detected by having a pair of clocks, instead of a
single clock, moving in each direction and letting an observer at rest
with each pair of clocks locally synchronize his own pair of clocks with
light signals and then have all the clocks symmetrically come to rest in
our frame, so that the original spacing of the clocks continues to be
maintained, but with the clocks from formerly different frame now
adjacent. We can compare the differences in the readings of two adjacent
pairs of clocks. If they are different, it indicates that we possess an
absolute velocity. If real time is not used, measurements can be
seriously distorted. Nature has little respect for illusory measurements
unless they combine to produce a real result. Relying on illusory
velocity measurements in calculating the impact of the kinetic energy of
a small meteoroid on a space ship might prove to be fatal. Even though
the mutual momentum is the same for identical rest masses, the
corresponding kinetic energy measurements would be slightly different
for low absolute velocities but would be very much different if one
observer has a high absolute velocity. [A.J. Brown, "A New Test for the
Anisotropy of Space," to be published.] Such an observer would then
suffer greater, if not devastating, damage depending on the degree to
which his absolute velocity [differs from] the absolute velocity of the
mass he is measuring. This is true because the energy is in units of mvv
and the relative velocity of an absolutely moving slower mass w.r.t. a
faster observer is greater than the velocity of the faster observer's
mass measured by the slower observer.
Adding an absolu
quote:De eerste die aan de SRT twijfelde was Albert Einstein zelf.Op zondag 25 juli 2004 17:27 schreef Haushofer het volgende:
....maar er wordt hier dus sterk getwijfeld aan de SRT.
quote:En?Op zondag 25 juli 2004 17:47 schreef Bard_Yttap het volgende:
[..]
De eerste die aan de SRT twijfelde was Albert Einstein zelf.
EInstein twijfelde ook aan QM en vergooide de laatste 30 jaar van zijn leven met het zoeken naar een universele theorie waarbij hij op de verkeerde stoomboot zat..
quote:Een gezond scepsis kan geen kwaad.Op zondag 25 juli 2004 17:27 schreef Haushofer het volgende:
Nou ja, heb het zelf ook niet helemaal doorgelezen, om eerlijk te zijn....maar er wordt hier dus sterk getwijfeld aan de SRT.
Toen Dirac aan het knoeien was met zijn vergelijkingen en de negatieve oplossingen zag, ging hij er ook vanuit dat een negatieve energie een oplossing zou kunnen zijn. Een nieuw deeltje.. dat kon niet.
Maar de redenatie dat een atoom altijd de laagste energie toestand zou innemen leidt tot de conclusie dat alle electronen in het atoom een negatieve energie zouden moeten hebben. En dan zou het spectrum er totaal anders uitzien. En dat was nog nooit waargenomen. Dus dan moest iets anders negatief zijn, een anti-electron dus.
quote:Niks en, want twijfel is de essentie van de (Popperiaanse) wetenschap. Of wil je terug naar het Empirisme?Op zondag 25 juli 2004 17:54 schreef Pietverdriet het volgende:
En?
quote:Hoe weet je dat hij op de verkeerde stoomboot zat? Zijn twijfel heeft de QM juist meer geholpen dan de blinde overtuiging van Niels Bohr in de Kopenhagen interpretatie. Zonder Einstein is het sterk de vraag of er ooit met EPR paren van quantum-states ge-experimenteerd zou zijn?!EInstein twijfelde ook aan QM en vergooide de laatste 30 jaar van zijn leven met het zoeken naar een universele theorie waarbij hij op de verkeerde stoomboot zat..
quote:Einstein was niet de enige die met dit idee kwam. Het heet niet voor niks EPR: Einstein, Podolsky, Rosen. Zoals het er nu voor staat, staat de QM ontzettend stevig in haar schoenen, en niemand heeft ooit deze theorie kunnen weerleggen. Je kunt idd blijven twijfelen, maar je kunt ook te lang twijfelen; op een gegeven moment kun je imho je tijd en energie beter in iets anders steken.Zijn twijfel heeft de QM juist meer geholpen dan de blinde overtuiging van Niels Bohr in de Kopenhagen interpretatie. Zonder Einstein is het sterk de vraag of er ooit met EPR paren van quantum-states ge-experimenteerd zou zijn?!
quote:Grappig dat je dat zegt, want tijd en energie was juist het vraagstuk waar Einstein zich mee bezig hield. Tijd en gravitatie(energie) kunnen niet zomaar zoek raken op Planckschaal zonder dat in een nieuwe theorie te verwerken. Wat Einstein dus zocht was één enkele kracht, die de bron was van de vier krachten die de kosmologie kent.Op zondag 25 juli 2004 19:31 schreef Haushofer het volgende:
Einstein was niet de enige die met dit idee kwam. Het heet niet voor niks EPR: Einstein, Podolsky, Rosen. Zoals het er nu voor staat, staat de QM ontzettend stevig in haar schoenen, en niemand heeft ooit deze theorie kunnen weerleggen. Je kunt idd blijven twijfelen, maar je kunt ook te lang twijfelen; op een gegeven moment kun je imho je tijd en energie beter in iets anders steken.
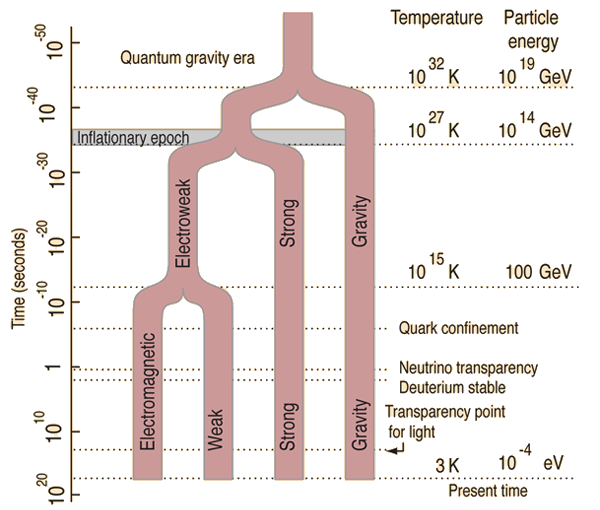
Het gaat dus in principe niet om het weerleggen van de QM, maar om een verklaring te vinden voor het ontbreken van gravitatie in de Quantum Mechanica en het ontbreken van een voorkeursrichting voor tijd en causaliteit. De door hem medebedachte EPR paradox toonde juist aan dat tijd ook op macroschaal een onbegrepen fenomeen is.
[ Bericht 4% gewijzigd door Bard_Yttap op 25-07-2004 20:03:57 ]
quote:Bron?Op maandag 26 juli 2004 14:47 schreef Haushofer het volgende:
Het Niels Boht instituut claimd de EPR paradox te hebben opgelost. Het probleem draait niet alleen om de instane informatieoverdracht, maar ook om een dubbelzinnige uitspraak die de QM doet over de meting. En die berust op een misverstand.
Dat ging meer over het verval van bv positronium in 2 fotonen, waarop je de polarisatie ging meten. Zo kwam je met ( op het eerste gezicht) 2 juiste redenaties over de waarschijnlijkheid, waarvan achteraf 1 natuurlijk niet juist was.
quote:De EPR paradox is juist dat de QM zegt dat je niet tegelijkertijd twee quantumeigenschappen precies kunt meten, terwijl dat bij een quantum EPR-paar wel zou moeten kunnen. De Heisenberg onzekerheidsrelatie, die hij tijdens zijn verblijf in het Niels Bohr instituut heeft opgesteld is dus door Albert Einstein, Boris Podolsky en Nathan Rosen (EPR) met een gedachtexperiment aan het wankelen gebracht en niet andersom. Daarom vroeg ik je om een specifieke bron.Op maandag 26 juli 2004 22:09 schreef Haushofer het volgende:
Tja, die bron zal internet zijnBen in April in Denemarken geweest voor een studiereis, en daar hebben we een lezing gehad over EPR. Hetgene wat ik er van heb meegekregen is dat die instane overdracht gerechtvaardigt kan worden, en werd gezien als een eigenschap ipv een probleem. Vaag ej, maar meer kan ik er ook niet over vertellen. Ikzelf heb met college de EPR paradox dan ook anders voorgeschoteld gekregen, en ging niet over die instantane overdracht.
Dat ging meer over het verval van bv positronium in 2 fotonen, waarop je de polarisatie ging meten. Zo kwam je met ( op het eerste gezicht) 2 juiste redenaties over de waarschijnlijkheid, waarvan achteraf 1 natuurlijk niet juist was.
Wie er uiteindelijk gelijk zal krijgen maakt filosofisch ook niet zoveel uit, want in beide gevallen is er iets "spooky" (zoals Einstein het noemde) aan de hand. Er zijn namelijk maar twee mogelijkheden, namelijk dat een EPR-paar verborgen (lokale) variabelen bezit of dat tijd en ruimte geen fundamentele rol spelen in de natuur. Ik ga van het laatste uit, omdat er meer aspekten mee verklaard worden.
De werkelijke uitkomst heeft wel een grote invloed op de "fabric of reality" en dus ook direct op de stringtheorie. Die theorie moet immers kloppen met of "verborgen lokale variabelen" of met "spooky action at a distance".
quote:Leg maar onder de scanner of overtypen en samenvatten, want het forum ondersteunt alle symbolen.Op dinsdag 27 juli 2004 17:39 schreef Haushofer het volgende:
Ej, dan heb je het anders begrepen dan ik. En ik heb toch echt de oplossing van dat probleem hier voor me liggen, alleen tikt het zo lastig met al die symbooltjes enzo. Het had iig niet met het onzekerheidsprincipe te maken.
Wat EPR wilde demonstreren is de onvolledigheid van de QM, door gebruik te maken van Heisenbergsonzekerheids relatie in de context van een EPR-paar.
quote:Zoals ik al zei kun je als gevolg van Heisenbergs eigen stelling niet tegelijkertijd (simultaan) twee verschillende quantumgrootheden (spin, positie, snelheid en energie) precies meten. Als je twee quantumfenomenen tegelijkertijd meet is één of allebei van de twee onnauwkeurig (statistisch onzeker).A proton with spin "up" along the x-axis has undefined spin along the y and z axes. You cannot simultaneously measure the x and y spin projections of a proton. EPR sought to demonstrate that this phenomenon could be exploited to construct an experiment that would demonstrate a paradox which they believed was inherent in the quantum-mechanical description of the world.
-edit- - - > bron
[ Bericht 24% gewijzigd door Bard_Yttap op 27-07-2004 21:47:14 (bron erbij) ]
quote:Ligt er aan wat de commutatie relatie is tussen de 2 grootheden. In het algemeen is de uitdrukkingAls je twee quantumfenomenen tegelijkertijd meet is één of allebei van de twee onnauwkeurig (statistisch onzeker).
(sigma A)*(sigma B)>= ( 1/2i *< [ A,B]>)^2
waarbij sigma de standaarddeviate is van resp de operator A en B, en [ ] de commutator is. Voor de plaats x en impuls p wordt dit dan ( omdat [x,p]=i*hstreep)
(sigma x)*(sigma p)>= (hstreep/2)
Puur analytisch gezien is het onzekerheidsprincipe van Heisenberg een gevolg van de ongelijkheid van Cauchy-Schwarz in een oneindig dimensionale Hilbert-ruimte.
Kzal ff kijken of ik die EPR-paradox normaal in tekst kan krijgen, en misschien post ik het morgen ofzo wel.
Een korte uitleg wordt trouwens gegeven in het ( alom omstreden) " introduction to quantummechanics" door Griffiths.
L-kwadraat en Lz, de z-component van L ( L is dan het hoekmoment, r uit p )
via [A, B+C]= [A,B] + [ A,C] en het feit dat de operatoren lineair zijn.
Het is dan ook altijd een keuze welke set operatoren je gebruikt voor het beschrijven van een systeem met bv 2 deeltjes, omdat de gekozen operatoren moeten commuteren.
Het voorbeeld gaat aan de hand van een elektron en een postitron, die interacteren, waarbij er 2 fotonen ontstaan. Zo’n foton heeft dus spin s=1, maar is wel massaloos; daarom zijn er slechts 2 verschillende m-waarden voor s=1 : m=1 en m=-1 (m=0 is er dus niet!).
m=1 noemen we RHC, met vector |R> oftewel Right Handed Circulation ( denk daarbij aan een vector naar boven gericht, en een beweging rechtsom die vector)
m=-1 noemen we LHC, met vector |L>, dus Left Handed Circulation. ( hierbij is de beweging dus links om )
Zo’n foton is gepolariseerd, en is ( ik kies x-y stelsel) in de x of in de y-richting gepolariseerd.
Je hebt dus de toestanden ( in vectoren uitgedrukt, in de Bra Ket notatie)
|x> , |y>, |R> en |L>
Dan kun je |R> en |L> uitdrukken in |x> en |y>, namelijk
|R>= (1/Sqrt2)*(|x>+i|y>)
|L>=(1/Sqrt2)*(|x>-i|y>)
Het elektron-positron paar staat stil, en dus is j=m=0 voor dit paar. De uitgezonden fotonen hebben dus m=1 en m=-1, en zullen dus beide RHC of beide LHC zijn.
( je verwacht het andersom, maar de richtingen van de fotonen zijn ook tegengesteld, en dus bezitten ze ,bekeken vanuit een stelsel, allebei de zelfde circulatie)
De kans op beide gebeurtenissen is 0,5.
Definieer nu |F>=|R1R2> - |L1L2> ( een assymetrische golffunctie)
En zet nu 2 waarnemers in het veld, traditiegetrouw heten ze Alice en Bob. Alice meet het ene foton, Bob het andere.
Bereken nu de kans es dat Bob x-polarisatie meet, en Alice y-polarisatie. Dit is simpel het inproduct van x1y2 met F, oftewel:
Kans= <x1y2|R1R2>-<x1y2|L1L2>=<x1|R1><y2|R2>-<x1|L1><y2|L2>=+i. Dus de kans is ( absolute waarde van i ) 1, oftewel 100%.
En dat klopt ook wel, want als je bv <x1x2|F> of <y1y2|F> uitrekent, krijg je 0.
Nu een scenario, wat Einstein opstelde. Het elektron-positron paar vervalt. En Alice meet….
1 Alice meet, en verkrijgt dus een RHC of een LHC resultaat
2 Alice kan dus voorspellen wat Bob zal meten, wanneer ze haar meetresultaat binnen krijgt. Zijn resultaat zal dus gelijk zijn aan die van Alice.
3 Ongeacht wat Alice ook gemeten heeft,het foton wat Bob meet is LHC of RHC.
4 Nu meet Bob |x> of |y>. De kans op beide toestanden is (1/Sqrt2)^2, oftewel ½.
5 Dus Bob meet in 50% van de gevallen |x>, en in 50% van de gevallen |y>
6 Maar als Alice |x> meet, dan meet Bob met kans 1 |y>, want <x1x2|F> was immers 0 !
En dat noemde Einstein een paradox. De “ paradox” ligt em in stap3. Einstein nam aan dat de beide metingen onafhankelijk van elkaar waren. Maar dat was natuurlijk niet zo: Alice verstoort de meting, waardoor Bob niet de gelijkmatige verdeling van |x> en |y> componenten zal krijgen.
Zo heb ik het probleem voorgeschoteld gekregen, er bestaan natuurlijk veel meer versies, altijd met niet-commutatieve grootheden. Het probleem met de instantane overdracht begrijp ik ook niet zo goed, maar dat is niet zo raar: er verschijnen elk jaar wel tig artikelen over dit probleem.
Het probleem hierin ligt vaak in het feit, dat men de filosofie van de klassieke mechanica over wil brengen naar de QM, terwijl het juist andersom moet zijn: de klassieke mechanica is een limietgeval van de QM.
In het ene doosje zit een zwarte bal en in het andere doosje zit een witte bal.
Dat weet ik, want dat heeft Haushofer mij verteld. Dus de twee ballen zijn gecorreleerd.
Ik loop nu naar de ene kant van de kamer met een doosje en Haushofer naar de andere kant van de kamer. De toestand van de bal (de kleur) is nog onbekend: het is nog niet bekend in welke eigentoestand hij zich bevindt.
Ik maak het doosje open, zie de kleur van de bal en ik weet gelijk wat de kleur is van de bal in het doosje van Haushofer, want in een flits springt de kleur van de bal naar de andere kleur dan die ik heb. Haushofer opent het doosje en ziet tot zijn verbazing dat ook zijn bal in het doosje naar de juiste eigentoestand gesprongen is.
Dus de onzekere toestand van de bal is veranderd in een zekere toestand: de kleur is gemeten.
Aan alle 6 de punten hierboven wordt voldaan.
Waarom dan moeilijk doen met QM als het zo makkelijk kan?
Die 2 ballen van ons zijn wel gecorreleerd, en dus worden ze beschreven door 1 golffunctie. Dus in principe wordt er "een signaal" verzonden van mij naar jou. Is het nou zo dat dat "signaal " eigenlijk niet opgevat kan worden als informatieoverdracht, omdat het niet vaststaat welke kleur ik krijg?
( heb toch nog wel een beetje moeite met die balletjes:) )
quote:Een beetje off-topicOp woensdag 18 augustus 2004 12:15 schreef Haushofer het volgende:
Op deze manier heb ik die "paradox" begrepen. Maar die "informatieoverdracht die sneller dan het licht gaat", daar zit ik nog mee.
Die 2 ballen van ons zijn wel gecorreleerd, en dus worden ze beschreven door 1 golffunctie. Dus in principe wordt er "een signaal" verzonden van mij naar jou. Is het nou zo dat dat "signaal " eigenlijk niet opgevat kan worden als informatieoverdracht, omdat het niet vaststaat welke kleur ik krijg?
( heb toch nog wel een beetje moeite met die balletjes:) )
De golffunctie strekt zich uit tussen de 2 balletjes, hoever ze ook uit elkaar gaan.
(Is op zich ook al een vraag. Tot hoever strekt de golfunctie zich uit.)
De signaaloverdracht gaat met de groepssnelheid dw/dk, en die is altijd kleiner dan de lichtsnelheid.
Je zou ook kunnen zeggen, dat het systeem van tevoren als wist welke kleur de balletjes hebben. En het is de persoon die meet, die het nog niet wist. Zo gauw hij een kleur gemeten heeft, weet hij vanzelf de andere kleur. De kansen ontstaan vanwege het gebrek aan informatie bij de persoon die meet.
Helaas zo werkt het niet. Niet lokale kansen in de QM kun je niet op deze manier aanpakken.
David Mermin,1985, Physics Today, 38 (no. 4) 38-47 heeft een poging gedaan om het gecombineerde spin-nul model van EPR met kansen te beschrijven. En hij komt tot de conclusie dat het niet mogelijk is: je kunt QM-kansen niet met het lokaal 'realistische' (klassieke) kansensysteem beschrijven.
Bell komt vervolgens met zijn theorema hierover.
Het balletjesverhaal is dus een klassieke interpretatie die geen QM equivalent kent, of andersom: de QM beschrijving van de balletjes is lokaal niet mogelijk. Heel raar eigenlijk.
De paradox begreep ik als volgt. "Zo gauw balletje 1 bekend is, volgt balletje 2 instantaan", is een klassieke beschrijving die QM niet voldoet. Informatie-overdracht met snelheden boven de lichtsnelheid zijn met de "klassieke" interpratie mogelijk. QM-isch echter niet.
Alain Aspect (1986), Experiments on EPR type correlations with pairs of visible photons, Quantum concepts in space and time; toont aan dat de QM correct is en het balletjesverhaal niet.
Je moet dus die asymmetrische golfunctie nemen voor spin plus en min een half. En dan kun je aantonen dat elke willekeurige andere combinatie van tegengestelde spinfuncties te herschrijven is als de oorspronkelijke door jou opgestelde functies.
Het was een soort laatste stuiptrekking van een aantal theoretici die zich met deze 10 D theorie hebben bezig gehouden.
En de laatste zin van de uitzending: "Misschien is het wel een zeepbel die op het punt staat te ontploffen", deed mij goed. Ik heb nooit veel heil gezien in deze theorie, die op vrijwel geen enkele experimentele manier te verifiëren valt. Er zit wel wat leuke wiskunde bij, maar dat is ook alles.
Nu kunnen de heren theoretici zich weer bezig gaan houden met meer realistische natuurkunde.
quote:Omdat-ie te moeilijk voor je is waarschijnlijk. Cognitieve dissonantie heet dat.Op zondag 12 september 2004 18:37 schreef Yosomite het volgende:
Zondagmiddag 12.9 de uitzending over snaartheorie eens bekeken.
Het was een soort laatste stuiptrekking van een aantal theoretici die zich met deze 10 D theorie hebben bezig gehouden.
En de laatste zin van de uitzending: "Misschien is het wel een zeepbel die op het punt staat te ontploffen", deed mij goed. Ik heb nooit veel heil gezien in deze theorie, die op vrijwel geen enkele experimentele manier te verifiëren valt.
quote:Op zondag 12 september 2004 18:54 schreef Koekepan het volgende:
[..]
Omdat-ie te moeilijk voor je is waarschijnlijk. Cognitieve dissonantie heet dat.
quote:Tja, als ik de ideeen zo bekijk ( zover ik ze nog enigszins begrijp dan ej) komt er wel een beetje het gevoel naar boven dat het iets bijzonders is, en misschien wel te mooi om niet waar te zijn. Dat mag misschien geen rechtvaardiging zijn voor een theorie, maar ja. Er mag wel meer nietOp zondag 12 september 2004 18:37 schreef Yosomite het volgende:
Zondagmiddag 12.9 de uitzending over snaartheorie eens bekeken.
Het was een soort laatste stuiptrekking van een aantal theoretici die zich met deze 10 D theorie hebben bezig gehouden.
En de laatste zin van de uitzending: "Misschien is het wel een zeepbel die op het punt staat te ontploffen", deed mij goed. Ik heb nooit veel heil gezien in deze theorie, die op vrijwel geen enkele experimentele manier te verifiëren valt. Er zit wel wat leuke wiskunde bij, maar dat is ook alles.
Nu kunnen de heren theoretici zich weer bezig gaan houden met meer realistische natuurkunde.
Serieus; ik denk dat het wel ergens heen gaat, en er schijnen al geometrische problemen mee te zijn opgelost, dus het is wel ergens goed voor ( mocht de fysische kant niet deugen)
Wat voor unificatie had je dan op het oog?
Ik als koppelaar op zondagavond?
Zover ben ik nog niet, 'k was x5 -x + 1 = 0 proberen op te lossen / te benaderen met de methode die een student uit Eindhoven heeft bedacht. Volgens Galois is dit (boven graad 5 in het algemeen) niet mogelijk. Maar deze doet in het bijzonder niet. Dus die test ik.
Maar in het kort, de theorie met resonanties U(1) x SU(2) x SU(3) zit QM aardig in elkaar. De "resonanties" in deze algebra, die de deeltjes voorspellen, klopt heel aardig.
Gekoppeld met de C (omplexen) & Q (uaternionen) & O (ctonionen) als Tensorproduct geeft deze Lie algebra (mits goed geïnterpreteerd) leuke resultaten.
En als ik er nu over nadenk, is dit gewoon de 10 D en 11D ruimte die ik probeer te elimineren omdat ik het physisch niet goed kan bevatten. Maar de correspontie tussen deze wiskunde en de experimentele resultaten is goed te noemen. Ik zal waarschijnlijk gedwongen worden, via Lie algebra / groepen om terug te keren naar het 10 D / 11 D model. Deze dimensies zijn waarschijnlijk dezelfde resonante dimensies in de snaartheorie. (Ik dacht er vanaf te zijn)
Maar om van SU(3) open of gesloten snaartjes te maken om de snaartheorie via de achterdeur naar binnen te halen. Vanavond niet meer in ieder geval.
[ Bericht 0% gewijzigd door Yosomite op 12-09-2004 21:31:04 ]
Overigens de tensor T = U(1) x SU(2) x SU(3) , transformeert net zo als de families en anti-families van quark en lepton spin (dat is heel handig om het een en ander te beschrijven).
was zeer boeiend. Vooral hoe je de groote van een superstring moet voorstellen
" slel je een Quark voor zo groot als het universum (zoals we het tot nu toe kennen)
en de superstring is dan zo groot als een boom ".
Maarja het is en blijft een theorie...
quote:Wat moet het anders zijn dan?Maarja het is en blijft een theorie...
quote:Het gaat erom dat je een theorie hebt die je wilt bewijzen.Op maandag 13 september 2004 10:09 schreef Haushofer het volgende:
[..]
Wat moet het anders zijn dan?
Waar zijn de bewijzen ( waarnemingen die door de ST worden voorspeld ) ?
Het gaat erom dat je je theorie wilt controleren, met ST is dit alleen zo lastig ( Op dit moment ), dat veel fysici ST alleen nog maar zien als een wiskunige theorie.
Ik zelf denk ook dat hij zich eerst moet bewijzen voor dat ik er in ga geloven, de vraag is alleen of dat nog gebeurt ( tijdens mijn leven
quote:Daar gaat het niet om. Het gaat om de uitspraak an sich. Wat wil je nog meer dan dat het een theorie is? Meer zal het nooit worden.Op maandag 13 september 2004 19:06 schreef srblackbird het volgende:
[..]
Het gaat erom dat je een theorie hebt die je wilt bewijzen.
Waar zijn de bewijzen ( waarnemingen die door de ST worden voorspeld ) ?
Het gaat erom dat je je theorie wilt controleren, met ST is dit alleen zo lastig ( Op dit moment ), dat veel fysici ST alleen nog maar zien als een wiskunige theorie.
Ik zelf denk ook dat hij zich eerst moet bewijzen voor dat ik er in ga geloven, de vraag is alleen of dat nog gebeurt ( tijdens mijn leven)
quote:Een theorie kan je praktisch benutten.....Op maandag 13 september 2004 19:28 schreef Haushofer het volgende:
[..]
Daar gaat het niet om. Het gaat om de uitspraak an sich. Wat wil je nog meer dan dat het een theorie is? Meer zal het nooit worden.
quote:ziet er interessant uit,Op maandag 31 mei 2004 12:46 schreef There_is_only_One het volgende:
Hier is een link naar "The Elegant Universe", bekijk de programma's en je weet wat het inhoudt.
http://www.pbs.org/wgbh/nova/elegant/program.html
kan iemand een link geven naar de .mov bestanden of ze online zetten
in mozilla kan ik die popup namelijk niet openen en IE crash (onverbeterlijk he microshoft)
quote:2+1=4-1Op maandag 31 mei 2004 16:22 schreef devilish1980 het volgende:
leuke is dat er een heleboel snaar theorieen zijn stuk of 10 hehe
1+2=4-1
lijken verschillend zijn het zelfde, same goes for this theory
quote:werkt dit?Op maandag 13 september 2004 21:08 schreef ooge het volgende:
[..]
ziet er interessant uit,
kan iemand een link geven naar de .mov bestanden of ze online zetten
in mozilla kan ik die popup namelijk niet openen en IE crash (onverbeterlijk he microshoft)
Quicktime - http://www.pbs.org/wgbh/nova/elegant/media2/3012_q_01.html
Real - http://www.pbs.org/wgbh/nova/elegant/media2/3012_r_01.html
quote:hij opent het dan wel alleen mozilla crasht er eveneens opOp dinsdag 14 september 2004 11:01 schreef pfaf het volgende:
[..]
werkt dit?
Quicktime - http://www.pbs.org/wgbh/nova/elegant/media2/3012_q_01.html
Real - http://www.pbs.org/wgbh/nova/elegant/media2/3012_r_01.html
moet ik weer windows opnieuw installeren denk ik
Dus je hoeft geen quantumveldentheorie te kennen, zoals bij alle andere boeken!
Ik denk dat ik dit boek binnenkort maar eens ga bestellen
quote:Bij ons op de uni kan je geen string theory volgenOp donderdag 16 september 2004 10:08 schreef Haushofer het volgende:
Kost geloof ik ca 60 euro ofzo, wordt bij ons op de uni ook gebruikt. Die andere String boeken zijn vaak al gauw 120 euro....
quote:Zeker, ik zou het er echt graag iets van af willen wetenOp donderdag 16 september 2004 11:10 schreef Haushofer het volgende:
'T is alleen een introductievak. ' t Is alleen de vraag of je zin in zoiets abstracts hebt.
Daarom ga ik ook zeker dat boek van Zwiebach lezen, en alvast wat beginnen aan ART
quote:ART ga ik volgend kwartaal volgen.Op donderdag 16 september 2004 13:29 schreef Pietjuh het volgende:
[..]
Zeker, ik zou het er echt graag iets van af willen weten
Daarom ga ik ook zeker dat boek van Zwiebach lezen, en alvast wat beginnen aan ART
quote:Uitgaande van je profiel doe je Farmacie? Ik denk dat de raaklijnen met die snaartheorie HEEL ver te zoeken zijn. Maar desalniettemin blijft het leuk natuurlijk.Op donderdag 16 september 2004 15:14 schreef ssebass het volgende:
Ik vind het heel interessant ik ga er ook maar eens een boek over lezen. Misschien steek ik er ook nog iets van op wat ik kan gebruiken voor mijn studie.
quote:Het zal je verbazen. Het concept op zich heeft er niet zoveel mee te maken, maar het heeft wel degelijk raakvlakken met farmacie. Het is inderdaad niet het meest directe en voor de hand liggende verband, maar het is er wel degelijk. Farmacie bestaat voornamelijk uit natuurkunde en scheikunde.Op donderdag 16 september 2004 18:55 schreef Haushofer het volgende:
[..]
Uitgaande van je profiel doe je Farmacie? Ik denk dat de raaklijnen met die snaartheorie HEEL ver te zoeken zijn. Maar desalniettemin blijft het leuk natuurlijk.
Maargoed het is natuurlijk bij mij voornamelijk uit interesse en niet uit het oogpunt van mijn studie. Alle wetenschappelijke doorbraken en nieuwe theorien mogen mijn interesse wel prikkelen
Ik moet een keuzevak doen om mijn bachelor af te ronden. Is er toevallig iemand die iets in deze richting weet wat wel leuk is om te doen aangezien ik qm erg interessant vind.
quote:Het zal je verbazen. Snaartheorie bestaat voornamelijk uit wiskunde.Op donderdag 16 september 2004 21:01 schreef ssebass het volgende:
[..]
Het zal je verbazen. Het concept op zich heeft er niet zoveel mee te maken, maar het heeft wel degelijk raakvlakken met farmacie. Het is inderdaad niet het meest directe en voor de hand liggende verband, maar het is er wel degelijk. Farmacie bestaat voornamelijk uit natuurkunde en scheikunde.
Maargoed het is natuurlijk bij mij voornamelijk uit interesse en niet uit het oogpunt van mijn studie. Alle wetenschappelijke doorbraken en nieuwe theorien mogen mijn interesse wel prikkelen
Ik moet een keuzevak doen om mijn bachelor af te ronden. Is er toevallig iemand die iets in deze richting weet wat wel leuk is om te doen aangezien ik qm erg interessant vind.
quote:Ja helaas schort het daar bij mij een beetje aan. Wiskunde komt overal in voor dus echt scheiden kun je het niet.Op donderdag 16 september 2004 21:29 schreef Haushofer het volgende:
[..]
Het zal je verbazen. Snaartheorie bestaat voornamelijk uit wiskunde.
Als ik jou profiel bekijk zie ik dat het ook niet echt jouw vakgebied is (correct me if I'm wrong), is dit bij jou ook louter interesse?
Verrek, ik studeer culturele antropologie ! En ik maar iedereen wijs maken dat ik natuurkunde studeer
Nee, ik studeer toch echt natuurkunde. Mooi vak.
quote:Ik wou je er al op aansprekenOp vrijdag 17 september 2004 10:48 schreef Haushofer het volgende:
( kom er opeens achter dat ik mn profiel al een paar maand niet heb ge update....)
Verrek, ik studeer culturele antropologie ! En ik maar iedereen wijs maken dat ik natuurkunde studeer
Nee, ik studeer toch echt natuurkunde. Mooi vak.
quote:Interessante docuOp maandag 31 mei 2004 12:46 schreef There_is_only_One het volgende:
Hier is een link naar "The Elegant Universe", bekijk de programma's en je weet wat het inhoudt.
http://www.pbs.org/wgbh/nova/elegant/program.html
*muziekje* Wilt U ook weten hoe het universum in elkaar zit? of relativiteit en quantummechanica te combineren zijn? wat extra dimensies inhouden? Voor de antwoorden op al uw vragen over alles wat zich om ons heen bevindt, hebben wij voor U de oplossing: snaartheorie, een revolutionaire theorie dat door de jaren heen geperfectioneerd is op basis van de bevindingen van o.a. Isaac Newton en Einstein en vele andere geleerden. Met deze theorie kan iedereen begrijpen hoe ons universum in elkaar zit en hoe het begonnen is! Bestel nu, en krijg een bundel waarin deze fantastische theorie beschreven staat. Want zeg nou zelf... wie wil er nou niet een keer over de schouder van God meekijken?
-------
Het blijft nog maar een theorie... Er zijn geen tastbare bewijzen voor, maar slechts een zooi wiskundige formules om het te onderbouwen. Het is leuk om te zien dat er een theorie is, waarmee bijna alles opeens te verklaren lijkt. Net als bij horoscopen dat mensen die dat lezen hebben, opeens bij bepaalde gebeurtenissen een verband gaan leggen met hun horoscoop... dat ze zeggen: "hé hoe is het mogelijk, dat klopt gewoon!"
Misschien bloeit er toch nog wat uit die theorie
quote:Dat idee van die snaren is al zo'n 30 jaar oud, en is geloof ik geintroduceerd door Veneziano. Voor een beschrijving van de sterke kernkracht, de kracht tussen de quarks.Misschien bloeit er toch nog wat uit die theorie . Maar bij het idee "snaren" denk ik: ze zullen wel gedacht hebben... "het is veel te abstract wat zich daar bevindt... laten we het maar een vorm geven. De vorm van een snaartje"
Over dat abstract-zijn...: het is meer zo dat het huidige model eigenlijk wat makkelijk is: deeltjes zijn 0 dimensionaal, en dat is toch enigszins vreemd: de ladings of massadichtheid wordt hierbij een distributie, wat ze een deltafunctie noemen. Dat beschrijft eigenlijk al geen fysische werkelijkheid meer.
quote:Volgens mij had Leonard Susskind het bedacht. Veneziano had naar mijn herrinering dat idee gebruikt om een bepaalde scattering berekening te doen, en zo dat zijn Veneziano formule kwamOp vrijdag 17 september 2004 19:35 schreef Haushofer het volgende:
[..]
Dat idee van die snaren is al zo'n 30 jaar oud, en is geloof ik geintroduceerd door Veneziano. Voor een beschrijving van de sterke kernkracht, de kracht tussen de quarks.
Over dat abstract-zijn...: het is meer zo dat het huidige model eigenlijk wat makkelijk is: deeltjes zijn 0 dimensionaal, en dat is toch enigszins vreemd: de ladings of massadichtheid wordt hierbij een distributie, wat ze een deltafunctie noemen. Dat beschrijft eigenlijk al geen fysische werkelijkheid meer.