KLB Klaagbaak
Klaag maar raak voor een knaak.
Nee, ik weet net iets meer van de materie dan jij.quote:Op dinsdag 9 mei 2017 23:29 schreef SecretPret het volgende:
[..]
Nee. Je bent echt hilarisch weet je dat?
quote:
Schrijf wat leuks in m'n gastenboek :) : http://secretpret.mygb.nl/
BTC : 3L9zW8LhLF4FpTjM8ojQUxeeEBjnJeE6z3
BTC : 3L9zW8LhLF4FpTjM8ojQUxeeEBjnJeE6z3
Dus ik heb drie appels, ik geef jou er 1 en dan ga jij mekkeren dat je eigenlijk maar 0.9999999999.. appel hebt gehad?
Een vel leeg papier kan altijd nog een mooie tekening worden.
Ik denk niet dat de conclusie van TS klopt, maar op zich wel een valide vraag:quote:
Dus ik heb drie appels, ik geef jou er 1 en dan ga jij mekkeren dat je eigenlijk maar 0.9999999999.. appel hebt gehad?
https://en.wikipedia.org/wiki/0.999...
Krekker is de bom!
Dan nog klopt mijn postquote:Op woensdag 10 mei 2017 07:19 schreef KreKkeR het volgende:
[..]
Ik denk niet dat de conclusie van TS klopt, maar op zich wel een valide vraag:
https://en.wikipedia.org/wiki/0.999...
0.3333... vind ik persoonlijk een slechte representatie van 1/3.
Een vel leeg papier kan altijd nog een mooie tekening worden.
Hzoquote:
[..]
Dan nog klopt mijn post
Schrijf wat leuks in m'n gastenboek :) : http://secretpret.mygb.nl/
BTC : 3L9zW8LhLF4FpTjM8ojQUxeeEBjnJeE6z3
BTC : 3L9zW8LhLF4FpTjM8ojQUxeeEBjnJeE6z3
Gefeliciteerd, TS. Je bent onhandig, bruut en bovendien geheel per ongeluk gestruikeld over het wiskundige bewijs dat 0,999999... gelijk staat aan 1.
Health In Harmony is een non-profitorganisatie die regenwoudgemeenschappen helpt met gezondheidszorg en duurzame inkomens in ruil voor bosbescherming, en zo tegelijk klimaatverandering en armoede aanpakt. - https://www.healthinharmony.org/
quote:
Gefeliciteerd, TS. Je bent onhandig, bruut en bovendien geheel per ongeluk gestruikeld over het wiskundige bewijs dat 0,999999... gelijk staat aan 1.
Bedankt dat je dat niet aankan.
Schrijf wat leuks in m'n gastenboek :) : http://secretpret.mygb.nl/
BTC : 3L9zW8LhLF4FpTjM8ojQUxeeEBjnJeE6z3
BTC : 3L9zW8LhLF4FpTjM8ojQUxeeEBjnJeE6z3
Ik kan het prima aan. Ik maak me alleen zorgen over de schaafwonden die je over hebt gehouden aan je struikelpartij. Gaat ie een beetje?quote:
Health In Harmony is een non-profitorganisatie die regenwoudgemeenschappen helpt met gezondheidszorg en duurzame inkomens in ruil voor bosbescherming, en zo tegelijk klimaatverandering en armoede aanpakt. - https://www.healthinharmony.org/
😂😂😂quote:
Dus ik heb drie appels, ik geef jou er 1 en dan ga jij mekkeren dat je eigenlijk maar 0.9999999999.. appel hebt gehad?
Wees gelukkig en positief.
quote:Op maandag 8 mei 2017 19:37 schreef SecretPret het volgende:
wiki page voor de mensen die het nog steeds weigeren te geloven: https://en.wikipedia.org/wiki/0.999...
Heb je het zelf wel gelezen?quote:In other words, the symbols "0.999…" and "1" represent the same number
One reason that infinite decimals are a necessary extension of finite decimals is to represent fractions. Using long division, a simple division of integers like 1/9 becomes a recurring decimal, 0.111..., in which the digits repeat without end. This decimal yields a quick proof for 0.999... = 1. Multiplication of 9 times 1 produces 9 in each digit, so 9 × 0.111... equals 0.999... and 9 × 1/9 equals 1, so 0.999... = 1:
Het is 1 driede geen 1 derde 
Taalverloederaars 
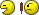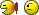
Taalverloederaars
Ik weet niet met welke wapens de derde wereldoorlog uitgevochten zal worden, maar de vierde wereldoorlog wordt uitgevochten met stokken en stenen.
1:3=1/3
2:3=2/3
3:3=3/3
3/3=1
Alleen met decimale getallen is 1/3 en 2/3 niet geheel weer te geven, daarom komt jou rideltje op 0.99999... uit.
Het is gewoon 1
____
2:3=2/3
3:3=3/3
3/3=1
Alleen met decimale getallen is 1/3 en 2/3 niet geheel weer te geven, daarom komt jou rideltje op 0.99999... uit.
Het is gewoon 1
____
Wat is de literprijs?
https://soundcloud.com/voor-fok/gesprek-met-de-vrouw-van-geert
https://soundcloud.com/voor-fok/gesprek-met-de-vrouw-van-geert
Ja, 0.999... = 1quote:
Schrijf wat leuks in m'n gastenboek :) : http://secretpret.mygb.nl/
BTC : 3L9zW8LhLF4FpTjM8ojQUxeeEBjnJeE6z3
BTC : 3L9zW8LhLF4FpTjM8ojQUxeeEBjnJeE6z3
Als er geen kinderen zijn, kun je niets delen, delen door 0 kan niet. Daar wordt je flink ziek van.quote:
3 delen door 3 is toch 0
Als ik 3 koekjes heb en die verdeel ik onder 3 kinderen houd ik 0 koekjes over.
Pff het ligt er maar aan wat je 3 is. Is het nummer 3? Dat is een algemeen abstract concept.
Is je drie echter iets dat fysiek is, drie knikkers of drie boterhammen dan is het logisch dat als je die gaat delen er niet een soort wiskunde monster is dat een kleine hap neemt als een soort belasting voor het delen van deze objecten.
Begin eerst eens met dat goed uit te leggen klaphark. Je begint direct met je zogehete kennis en zelfs dan maakt die hele kleine marge niet uit want die rond je af... Alsof het uitmaakt...
[ Bericht 11% gewijzigd door #ANONIEM op 11-05-2017 08:22:16 ]
Is je drie echter iets dat fysiek is, drie knikkers of drie boterhammen dan is het logisch dat als je die gaat delen er niet een soort wiskunde monster is dat een kleine hap neemt als een soort belasting voor het delen van deze objecten.
Begin eerst eens met dat goed uit te leggen klaphark. Je begint direct met je zogehete kennis en zelfs dan maakt die hele kleine marge niet uit want die rond je af... Alsof het uitmaakt...
[ Bericht 11% gewijzigd door #ANONIEM op 11-05-2017 08:22:16 ]
Jij en 3 kinderen zijn toch 4 personen, of niet dan?quote:
3 delen door 3 is toch 0
Als ik 3 koekjes heb en die verdeel ik onder 3 kinderen houd ik 0 koekjes over.
spierbal met 3 koekjes - 3 koekjes voor een aantal kinderen = 0
Dus feitelijk gezien deel jij niks, want je deelt niet mee.
Tenzij je zelf 1 van die kinderen bent (en dat zou gezien je denkwijze best kunnen) en dan deel je de 3 koekjes tussen jezelf en nog 2 andere kinderen. En heb je dus 1/3 koekje per kind.
Dan zijn er twee koekjes kwijt!quote:
[..]
Tenzij je zelf 1 van die kinderen bent (en dat zou gezien je denkwijze best kunnen) en dan deel je de 3 koekjes tussen jezelf en nog 2 andere kinderen. En heb je dus 1/3 koekje per kind.
quote:
Nee hoor. 3 past 1 keer in 3 dus het antwoord is 1.
Schrijf wat leuks in m'n gastenboek :) : http://secretpret.mygb.nl/
BTC : 3L9zW8LhLF4FpTjM8ojQUxeeEBjnJeE6z3
BTC : 3L9zW8LhLF4FpTjM8ojQUxeeEBjnJeE6z3
|
|
