Star Killer Base in Star Wars kan de volledige energie van hele sterren opzuigen.
We weten dankzij Einstein dat energie = massa
Star Killer Base zal dan de massa van een ster hebben op het moment dat de volledige energie van een ster opgezogen is.
Op dat moment heeft Star Killer base de gravitatie van een witte dwerg.
Op een witte dwerg ster zal de gravitatiekracht iets van 300.000 keer groter zijn dan op aarde.
Alle levende wezens op Star Killer base zullen doodgedrukt worden tot ze minder dan een micrometer dik zijn. Op Star Killer base groeien bomen. Dit zal ook onmogelijk zijn.
In de film wordt onderschat hoeveel energie een ster heeft. Stel onze ster zou supernova gaan, dan zouden niet alleen alle planeten in onze zonnestelsel weggevaagd worden, zelfs leven dat zich op enkele lichtjaren afstand bevindt zal weggevaagd worden.
Interstellar
Bij Interstellar draait er een planeet om een zwart gat, waar de ruimtevaarders heen gaan. Ik schat dat de straal van het zwarte gat in de film ongeveer 300.000 km is. De massa van het zwarte gat is dan ongeveer 100.000 zonnemassa's.
De maximale afstand waarbij een foton in een baan om een zwart gat kan draaien is ongeveer 1,5 keer de straal van het zwart gat. Als het foton dichterbij komt, wordt het verzwolgen door het gat. Op deze afstand is de tijddilatatie ongeveer 50%. Een planeet kan dus onmogelijk in een straal draaien dat nog korter is dan 1,5 keer de straal. Maximale tijddilatatie voor een planeet dat in een stabiele baan om een zwart gaat draait kan dus nooit groter zijn dan 50%. In de film staat het op de planeet blijven van een uur gelijk aan het verstrijken van 7 jaar op aarde. Dit is dus onmogelijk.
Dat vond je aannemelijker dan de tijddilatatie?
Dus niet echt Star Wars. Slot please.
Tegen de tijd dat je een techniek hebt uitgevonden om de Energie van hele Sterren op te zuigen heb je vast ook wel iets van een techniek uitgevonden om die opgeslagen energie zodanig af te schermen dat je gewoon in de buurt van die techniek kan zijn en er zelfs bomen op kan laten groeien en misschien zelfs bloemen er.quote:Op zaterdag 24 december 2016 09:12 schreef polderturk het volgende:
Star Wars TFA
Star Killer Base in Star Wars kan de volledige energie van hele sterren opzuigen.
We weten dankzij Einstein dat energie = massa
Star Killer Base zal dan de massa van een ster hebben op het moment dat de volledige energie van een ster opgezogen is.
Op dat moment heeft Star Killer base de gravitatie van een witte dwerg.
Op een witte dwerg ster zal de gravitatiekracht iets van 300.000 keer groter zijn dan op aarde.
Alle levende wezens op Star Killer base zullen doodgedrukt worden tot ze minder dan een micrometer dik zijn. Op Star Killer base groeien bomen. Dit zal ook onmogelijk zijn.
In de film wordt onderschat hoeveel energie een ster heeft. Stel onze ster zou supernova gaan, dan zouden niet alleen alle planeten in onze zonnestelsel weggevaagd worden, zelfs leven dat zich op enkele lichtjaren afstand bevindt zal weggevaagd worden.
Interstellar
Bij Interstellar draait er een planeet om een zwart gat, waar de ruimtevaarders heen gaan. Ik schat dat de straal van het zwarte gat in de film ongeveer 300.000 km is. De massa van het zwarte gat is dan ongeveer 100.000 zonnemassa's.
De maximale afstand waarbij een foton in een baan om een zwart gat kan draaien is ongeveer 1,5 keer de straal van het zwart gat. Als het foton dichterbij komt, wordt het verzwolgen door het gat. Op deze afstand is de tijddilatatie ongeveer 50%. Een planeet kan dus onmogelijk in een straal draaien dat nog korter is dan 1,5 keer de straal. Maximale tijddilatatie voor een planeet dat in een stabiele baan om een zwart gaat draait kan dus nooit groter zijn dan 50%. In de film staat het op de planeet blijven van een uur gelijk aan het verstrijken van 7 jaar op aarde. Dit is dus onmogelijk.
Ik denk eerlijk gezegd dat dit niet noodzakelijk impliceert, dat de film volledig wetenschappelijk correct is (wat de film volgens mij niet is, en ook niet bedoeld is om te zijn).quote:
Ik heb Interstellar niet nagerekend, maar volgens mij zat Kip Thorne achter de algemene relativiteit van de film.
Echter de mooie beelden van het zwarte gat met de accretieschijf, en ook de beelden wanneer ze door het wormgat gaan, zouden wel correct zijn. (http://aapt.scitation.org/doi/full/10.1119/1.4916949)
Op het arXiv staan ook wel wat artikelen over de wetenschap achter deze film. Volgens mij zijn wormgaten überhaupt nogal exotisch.quote:
[..]
Ik denk eerlijk gezegd dat dit niet noodzakelijk impliceert, dat de film volledig wetenschappelijk correct is (wat de film volgens mij niet is, en ook niet bedoeld is om te zijn).
Echter de mooie beelden van het zwarte gat met de accretieschijf, en ook de beelden wanneer ze door het wormgat gaan, zouden wel correct zijn. (http://aapt.scitation.org/doi/full/10.1119/1.4916949)
Ja, dat is weer het gebruikelijke tov-doenerij van Krauss. Het blijft een Hollywood-productie, natuurlijk.quote:
Op tov?quote:
[..]
Ja, dat is weer het gebruikelijke tov-doenerij van Krauss. Het blijft een Hollywood-productie, natuurlijk.
Popi, hoe je het wilt noemen.quote:
Ah zo. Nou ja, een film over zo'n onderwerp kan best een Hollywood-productie zijn zonder een complete karikatuur van de wetenschap te maken, lijkt me.quote:
Als ik even reflecteer op mijn eigen vakgebied, ICT, dan zit er ook een duidelijk verschil tussen - zeg - de film "War Games", en de serie Mr. Robot. Het verweer "de gemiddelde kijker ziet dat verschil toch niet" vind ik niet zo sterk. Ten eerste zien velen dat verschil wel, ten tweede is het geen essentieel verschil voor Hollywood. Dus waarom dan niet proberen om het enigszins realistisch te houden?
Een Kerr zwart gat heeft twee photon spheresquote:
(Interstellar:) De tijdsdilatatie is inderdaad onmogelijk onder aanname dat het zwarte gat niet roteert (Schwarzschild metriek). Echter binnen de Kerr-metriek voor een roterend zwart gat kan het als ik me goed herinner wel, alhoewel zelfs dan het zwarte gat uitzonderlijk snel zou moeten roteren, maar goed.
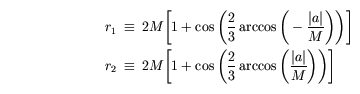
In deze vergelijkingen zijn de waarden c en G op 1 gezet
a is het angular momentum. Als deze de waarde 0 heeft, dan krijg je de photon sphere van een Schwarzschild zwart gat.
Tijdsdilatatie bij een Schwarzschild zwart gat als je op de photon sphere bent::
ds^2 = (1-2MG/c^2r)dt^2
r = 3MG/c^2
ds^2 = (1-2/3)dt^2
ds^2= 1/3*dt^2
ds = wortel(1/3)*dt
ds = 0,58*dt
Dus de tijddilatatie op de photon sphere is minder dan 50%
Zoals je in de afbeelding kan zien ligt de planeet op ongeveer 2 keer de Schwarzschild radius. Dat is 4GM/c^2. De planeet ligt nog verder weg dan de photon sphere. Dus nog minder tijddilatatie
Je krijgt dan
ds^2 = (1-2/4)*dt^2
ds^2 = 1/2*dt^2
ds = wortel(1/2)*dt
ds = 0,71*dt
Laten we nu naar een Kerr zwart gat kijken dat met 50% van het licht draait
De binnenste photon sphere wordt:
r1 = 2GM/c^2(1 + cos(2/3arccos(-a/cM))
r1 = 2GM/c^2(1+0,17)
r1 = 2GM/c^2(1,17)
r1 = 1,17*Rs (Rs is Schwarzschild radius)
Dus de binnenste photon spere ligt dan op 1,17* Schwarzschild radius. Bij een Schwarzschild zwart gat is dat 1,5 keer Rs.
De buitenste photon sphere.
r2 = 2GM/c^2(1 + cos(2/3arccos(-a/cM))
r2= 1,76 Rs
Wat is de tijddilatatie van een Kerr zwart gat op 1,17 RS (binnenste photon sphere)
ds^2 = (1-rS*r/rho^2)*dt^2
rho^2 = r^2 + a^2cos(theta) = r^2 + 1/4 (als we hoek theta = 0 nemen wordt cos(theta) = 1)
ds^2 = (1-rS*1,17*Rs/(1,17^2*Rs^2 + 1/4))*dt^2
ds^2 = (1-0,85)dt^2
ds^2 = (0,15)*dt^2
ds = wortel(0,15)*dt^2
ds = 0,39*dt
Dus de tijddilatatie wordt maar ietsjes sterker.
Inderdaad, maar dit geldt zoals je zelf zegt voor een rotatiesnelheid van 0.5c. Zoals altijd in de relativiteit divergeert het resultaat voor v->c. Je kunt dus om het even welke dilatatie krijgen, zolang je de rotatiesnelheid maar hoog genoeg neemt.quote:
Laten we nu naar een Kerr zwart gat kijken dat met 50% van het licht draait
De binnenste photon sphere wordt:
(...)
Dus de tijddilatatie wordt maar ietsjes sterker.
(...)
Het is ondertussen al een jaar geleden dat ik zelf de afleiding heb gemaakt, maar wat je kunt doen is de rotatiesnelheid als onbekende nemen. Je berekent dan de nodige rotatie om de tijdsdilatatie in de film te bekomen. Ik weet het niet meer zeker, maar ik kwam denk ik iets uit van toch minstens een rotatiesnelheid van 95% de lichtsnelheid.
Je kunt dan vragen beginnen stellen, zoals of deze immense rotatie niet nog hogere golven zou veroorzaken op de nabije planeet. Maar hierover heb ik niet verder nagedacht.
Ik ga een poging doen, al gaat het niet helemaal kloppen. Het is meer om een beeld te geven
Volgens Newtonian mechanics is de kinetische energie van een object dat in een baan draait gelijk aan de helft van de potentiele energie
Fz = Fmpz
GmM/r^2 = mv^2/r
als je dit oplost krijg je v = wortel (GM/r)
KE = (1/2)*m*v^2
KE = (1/2)*m*GM/r = (1/2)*GmM/r = - (1/2)PE
Nu ga ik de kinetische energie uitrekenen van een object van 1 kg dat om een zwart gat draait op een afstand van 1,5*Rs (1,5 keer de Schwarzschild radius). Rs = 2GM/c^2, dus 1,5*Rs wordt 3GM/c^2)
(deze stap mag eigenlijk niet omdat ik van Newtonian mechanics de overstap maak naar algemene relativiteit)
KE = (1/2)*(GmMc^2) / (3GM) = (1/2)*mc^2/3 = 1/6mc^2
Bij relativistische snelheden wordt de KE als volgt berekend:
KE = mc^2/wortel(1-v^2/c^2) - mc^2
mc^2/wortel(1-v^2/c^2) = KE + mc^2
1 / wortel(1-v^2/c^2) = (KE + mc^2)/mc^2
wortel(1-v^2/c^2) = mc^2 / (KE + mc^2)
1 - v^2/c^2 = (mc^2)^2 / (KE + mc^2)^2
- v^2/c^2 = (mc^2)^2 / (KE + mc^2)^2 -1
v^2 = (1- (mc^2)^2 / (KE + mc^2)^2)*c^2
v = wortel((1- (mc^2)^2 / (KE + mc^2)^2)) * c
KE = (1/6)*mc^2 invullen:
v = wortel((1- (mc^2)^2 / ((1/6)*mc^2 + mc^2)^2)) * c
v = wortel((1- (mc^2)^2 / ((7/6)*mc^2)^2)) * c
v = 0,52 * c
Bij een snelheid van 0,52c is er ook geen gigantische tijddilatatie.
Je zal dan uiteindelijk een afstand krijgen van in de orde 1,0001*Rs ofzo.quote:
[..]
Inderdaad, maar dit geldt zoals je zelf zegt voor een rotatiesnelheid van 0.5c. Zoals altijd in de relativiteit divergeert het resultaat voor v->c. Je kunt dus om het even welke dilatatie krijgen, zolang je de rotatiesnelheid maar hoog genoeg neemt.
Het is ondertussen al een jaar geleden dat ik zelf de afleiding heb gemaakt, maar wat je kunt doen is de rotatiesnelheid als onbekende nemen. Je berekent dan de nodige rotatie om de tijdsdilatatie in de film te bekomen. Ik weet het niet meer zeker, maar ik kwam denk ik iets uit van toch minstens een rotatiesnelheid van 95% de lichtsnelheid.
Je kunt dan vragen beginnen stellen, zoals of deze immense rotatie niet nog hogere golven zou veroorzaken op de nabije planeet. Maar hierover heb ik niet verder nagedacht.
De planeet uit de film moet dan zeeeer dicht tegen het zwarte gat aankomen. Hij moet er bijna tegenaan rollen. In de film is dat echter niet zo. Kijk maar. De afstand van de planeet tot het zwarte gat is groter dan Rs (de straal van het zwarte gat). Als hij bijna tegen het zwarte gat aan zou rollen, dan zou de dilatatie aan de ene kant van de planeet ook veel sterker zijn dan aan de andere. Aan de ene kant van de planeet zou de afstand dan 1,0001*Rs zijn en aan de andere kant 1,05*Rs ofzo.
De afstand tussen planeet en centrum van het zwarte gat ligt vast, als je aanneemt dat de planeet zich op een stabiele cirkelbaan bevindt. Het is niet deze afstand die de tijdsdilatatie de pan uit doet swingen: dat doet de rotatiesnelheid van het zwarte gat in de limiet v->c, binnen de Kerr-metriek.quote:
[..]
Je zal dan uiteindelijk een afstand krijgen van in de orde 1,0001*Rs ofzo.
De planeet uit de film moet dan zeeeer dicht tegen het zwarte gat aankomen. Hij moet er bijna tegenaan rollen. In de film is dat echter niet zo. Kijk maar. De afstand van de planeet tot het zwarte gat is groter dan Rs (de straal van het zwarte gat). Als hij bijna tegen het zwarte gat aan zou rollen, dan zou de dilatatie aan de ene kant van de planeet ook veel sterker zijn dan aan de andere. Aan de ene kant van de planeet zou de afstand dan 1,0001*Rs zijn en aan de andere kant 1,05*Rs ofzo.
Als een planeet daadwerkelijk een hele ster zou opzuigen, dan zou het ook de massa van de ster krijgen. Je krijgt dan de gravitatiekracht van een witte dwerg. Op een witte dwerg is de gravitatiekracht 100.000 keer groter dan op aarde. Mensen zouden platgedrukt worden totdat ze platter zouden zijn dan een millimeter.
Starkiller base had net een hele ster opgezogen.
Een supernova kan leven op een lichtjaar afstand vernietigen (ongeveer 10 biljoen km), maar de vernietiging van Starkiller base, die net een hele ster opgezogen heeft, levert maar een miezerige explosie op (in vergelijking met een supernova).
