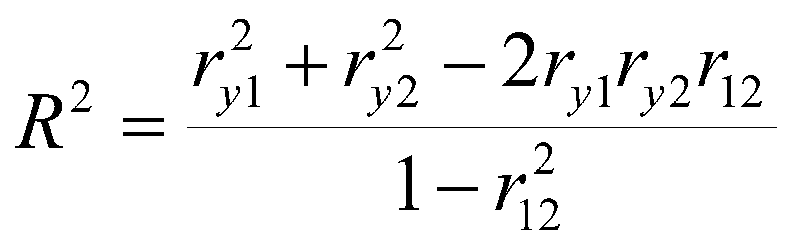SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ik weet niet uit hoeveel categorieŽn opleiding en leeftijd bestaan maar je moet dan wel even oppassen dat je niet in de problemen raakt met je degrees of freedom. Je hebt namelijk nogal weinig observeringen en voor elke onafhankelijke variabele heb je wel 5 waarnemingen nodig.quote:Op zaterdag 28 november 2015 12:40 schreef Bruinvis het volgende:
Hallo allemaal,
Ik ben momenteel bezig met het analyseren van data voor mijn masterscriptie. Nu is er iets waar ik niet helemaal uit kom. Mijn plan is om een meervoudige regressie analyse uit te voeren. Hiervoor heb ik 3 controlevariabelen (leeftijd, geslacht, opleiding), 3 onafhankelijke variabelen (op interval niveau) en 1 afhankelijke variabele (ook op interval niveau). Leeftijd en opleiding zijn nu ordinale variabelen en daarom heb ik hiervan dummies gemaakt, zodat ik ze kan meenemen in de regressie. De klassen die het meest voorkomen beschouw ik als de referentie-variabele, deze dummy neem ik dus niet mee in de regressie.
Nu mijn vraag: ik heb een steekproef van 57 personen, waarvan 3 de controlevariabelen in de enquete niet hebben ingevuld. Nu vraag ik mij af hoe deze missing values worden meegenomen in de dummies. Zoals ik het nu zie corresponderen de missing values (die ik aangeef met een '9') met geen van de dummies en worden deze dus automatisch (en onjuist) gezien als behorende tot de referentie-variabele? Moet ik daarom nog een dummy aanmaken voor deze missing values?
Dan nog een andere vraag. Ik doe een hiŽrarchische regressie analyse omdat ik wil corrigeren voor de controlevariabelen. Dus ik doe de controlevariabelen in 1 blok, de 2 onafhankelijke variabelen van de theorie die ik wil testen in blok 2, en de laatste onafhankelijke variabele in blok 3. Maar kunnen alle dummie variabelen (dus van leeftijd en opleiding) wel samen in 1 blok worden toegevoegd?
Alvast heel erg bedankt voor het meedenken!


Ik heb ze er idd uitgegooid door te kiezen voor 'exclude cases listwise'. Bedankt voor je reactie!quote:Op zaterdag 28 november 2015 13:38 schreef wimjongil het volgende:
Kun je die drie observaties er niet gewoon uit flikkeren? Scheelt een hoop gedoe.


Ik heb er inderdaad vooraf niet bij stilgestaan dat ik dummy variabelen zou moeten gebruiken en dus een grotere steekproef nodig zou hebben, achteraf niet erg handig. Ik was simpelweg uitgegaan van een totaal van 6 onafhankelijke variabelen.quote:Op zaterdag 28 november 2015 14:14 schreef MCH het volgende:
[..]
Ik weet niet uit hoeveel categorieŽn opleiding en leeftijd bestaan maar je moet dan wel even oppassen dat je niet in de problemen raakt met je degrees of freedom. Je hebt namelijk nogal weinig observeringen en voor elke onafhankelijke variabele heb je wel 5 waarnemingen nodig.
De categorieŽn opleiding en leeftijd bestaan beide uit 4 categorieŽn dus ik heb daarvoor per variabele 3 dummies meegenomen in de regressie. Daarnaast heb ik dus nog 1 nominale controlevariabele (geslacht) en 3 onafhankelijke variabelen. Daarvoor zou ik dan minimaal 50 observaties nodig hebben toch?
Zou je anders aanraden leeftijd of opleiding bijvoorbeeld weg te laten uit de analyse?


Als jij in je theoretisch kader over deze variabelen geschreven hebt en ook hypotheses over hebt opgesteld dan is het zonde om dat er nu weer uit te slopen. Je kan twee dingen doen. Als je ruim in de tijd zit nog wat extra data verzamelen of verder gaan met deze data en daar bij de limitations een vermelding over schrijven.quote:Op zaterdag 28 november 2015 14:31 schreef Bruinvis het volgende:
[..]
Ik heb er inderdaad vooraf niet bij stilgestaan dat ik dummy variabelen zou moeten gebruiken en dus een grotere steekproef nodig zou hebben, achteraf niet erg handig. Ik was simpelweg uitgegaan van een totaal van 6 onafhankelijke variabelen.
De categorieŽn opleiding en leeftijd bestaan beide uit 4 categorieŽn dus ik heb daarvoor per variabele 3 dummies meegenomen in de regressie. Daarnaast heb ik dus nog 1 nominale controlevariabele (geslacht) en 3 onafhankelijke variabelen. Daarvoor zou ik dan minimaal 50 observaties nodig hebben toch?
Zou je anders aanraden leeftijd of opleiding bijvoorbeeld weg te laten uit de analyse?


Ik zit helaas niet erg ruim in de tijd nee, dus dan ga ik voor de tweede optie! Bedankt nogmaals!quote:Op zaterdag 28 november 2015 17:59 schreef MCH het volgende:
[..]
Als jij in je theoretisch kader over deze variabelen geschreven hebt en ook hypotheses over hebt opgesteld dan is het zonde om dat er nu weer uit te slopen. Je kan twee dingen doen. Als je ruim in de tijd zit nog wat extra data verzamelen of verder gaan met deze data en daar bij de limitations een vermelding over schrijven.


Stel we hebben een stationair time-series waarvan we het aantal units van tijd in memory willen bepalen. Kijken we naar de partial of normale autocorrelatie?


Autocorrelatie met lagged dependent variable loopt in theorie oneindig door, dus het logische antwoord is partial.quote:Op dinsdag 8 december 2015 23:59 schreef Sokz het volgende:
Stel we hebben een stationair time-series waarvan we het aantal units van tijd in memory willen bepalen. Kijken we naar de partial of normale autocorrelatie?


Verliezen op een gegeven moment significantie though.quote:Op woensdag 9 december 2015 14:33 schreef ibrkadabra het volgende:
[..]
Autocorrelatie met lagged dependent variable loopt in theorie oneindig door, dus het logische antwoord is partial.


Is dat juist ook niet wat je wil weten uiteindelijk? Bijvoorbeeld om te voorspellen hoeveel periodes ervoor nog een goede voorspeller is van je sales.quote:Op woensdag 9 december 2015 23:15 schreef Sokz het volgende:
[..]
Verliezen op een gegeven moment significantie though.Thanks beiden!


Ja, maar dat doe je dus met de pacf. Als je een AR(1) proces hebt, heeft t-2 ook nog een invloed op je huidige waarde, maar niet direct.quote:Op woensdag 9 december 2015 23:18 schreef MCH het volgende:
[..]
Is dat juist ook niet wat je wil weten uiteindelijk? Bijvoorbeeld om te voorspellen hoeveel periodes ervoor nog een goede voorspeller is van je sales.
Op dinsdag 23 november 2010 02:22 schreef Braddie het volgende:
Haal van internet af man.
Haal van internet af man.


Klopt! :p Alleen als je een coefficient van 0.97 hebt bijv. voor je 1e lag (als we een AR(1) beschouwen), dan heb je pas bij lag 100 ofzo geen significantie meer als je de ACF gebruikt.quote:Op woensdag 9 december 2015 23:15 schreef Sokz het volgende:
[..]
Verliezen op een gegeven moment significantie though.Thanks beiden!


Beste allen,
Ik heb een vraag mbt SPSS. Ik wil opleidingsniveau categoriseren. Ik heb in mijn enquÍte gevraagd naar welke opleiding iemand gevolgd heeft en deze antwoordcategorieŽn gebruikt: Lagere school, VMBO, MBO, HAVO, VWO, HBO/WO. Nu wil ik deze categoriseren naar laagopgeleid, middelbaar opgeleid en hoogopgeleid volgens de theorie die ik gebruik. Dit is gelukt door 'recode into different variables'. Ik heb laagopgeleid een waarde van 10, middelbaar een waarde van 11 en hoogopgeleid een waarde van 12 gegeven. Wanneer ik nu een simpele correlatie uitvoer met een andere variabele, krijg ik resultaten.
Echter, ik wil graag deze 3 groepen scheiden, waardoor ik per groep kan kijken of het correleert ja of nee. Dit doe ik door 'split file' en dan 'organize output by groups'. Helaas krijg ik nu bij de correlatie alleen maar puntjes te zien (bij Kendall's Tau; overigens ook bij de andere, maar die heb ik niet nodig). Heeft iemand enig idee wat ik fout doe? Ik kom er echt niet uit en moet maandag scriptie inleveren
[ Bericht 1% gewijzigd door fetX op 19-12-2015 13:28:10 ]
Ik heb een vraag mbt SPSS. Ik wil opleidingsniveau categoriseren. Ik heb in mijn enquÍte gevraagd naar welke opleiding iemand gevolgd heeft en deze antwoordcategorieŽn gebruikt: Lagere school, VMBO, MBO, HAVO, VWO, HBO/WO. Nu wil ik deze categoriseren naar laagopgeleid, middelbaar opgeleid en hoogopgeleid volgens de theorie die ik gebruik. Dit is gelukt door 'recode into different variables'. Ik heb laagopgeleid een waarde van 10, middelbaar een waarde van 11 en hoogopgeleid een waarde van 12 gegeven. Wanneer ik nu een simpele correlatie uitvoer met een andere variabele, krijg ik resultaten.
Echter, ik wil graag deze 3 groepen scheiden, waardoor ik per groep kan kijken of het correleert ja of nee. Dit doe ik door 'split file' en dan 'organize output by groups'. Helaas krijg ik nu bij de correlatie alleen maar puntjes te zien (bij Kendall's Tau; overigens ook bij de andere, maar die heb ik niet nodig). Heeft iemand enig idee wat ik fout doe? Ik kom er echt niet uit en moet maandag scriptie inleveren
[ Bericht 1% gewijzigd door fetX op 19-12-2015 13:28:10 ]


Je bent sowieso al helemaal verkeerd bezig door een correlatiemaat te berekenen over een categorische variabele. Wiskundig gezien is het nog wel mogelijk om een correlatiemaat te berekenen aangezien je 2 variabelen hebt met verschillende waarden, maar inhoudelijk gezien is het onzinnig aangezien "Opleidingsniveau" niet van intervalniveau of hoger is... snappie? Dus dat is al fout #1.quote:Op zaterdag 19 december 2015 13:21 schreef fetX het volgende:
Beste allen,
Ik heb een vraag mbt SPSS. Ik wil opleidingsniveau categoriseren. Ik heb in mijn enquÍte gevraagd naar welke opleiding iemand gevolgd heeft en deze antwoordcategorieŽn gebruikt: Lagere school, VMBO, MBO, HAVO, VWO, HBO/WO. Nu wil ik deze categoriseren naar laagopgeleid, middelbaar opgeleid en hoogopgeleid volgens de theorie die ik gebruik. Dit is gelukt door 'recode into different variables'. Ik heb laagopgeleid een waarde van 10, middelbaar een waarde van 11 en hoogopgeleid een waarde van 12 gegeven. Wanneer ik nu een simpele correlatie uitvoer met een andere variabele, krijg ik resultaten.
Echter, ik wil graag deze 3 groepen scheiden, waardoor ik per groep kan kijken of het correleert ja of nee. Dit doe ik door 'split file' en dan 'organize output by groups'. Helaas krijg ik nu bij de correlatie alleen maar puntjes te zien (bij Kendall's Tau; overigens ook bij de andere, maar die heb ik niet nodig). Heeft iemand enig idee wat ik fout doe? Ik kom er echt niet uit en moet maandag scriptie inleveren
Fout #2 die je maakt is dat je, na het gebruiken van split file, je wederom een correlatiemaat probeert te berekenen tussen variabele "Opleidingsniveau" en de andere variabele, maar dan per groep van opleidingsniveau. Maar, alle mensen in ťťn split-groep hebben natuurlijk dezelfde score op Opleidingsniveau. Dus nu is het uitrekenen van een correlatiemaat behalve onzinnig, ook nog eens wiskundig onmogelijk geworden.
Overigens vind ik het ook raar dat je de categorieŽn aanduid met waardes (10, 11, 12). Niet echt fout, maar wel ongebruikelijk. Waarom niet (1, 2, 3) of (0, 1, 2)?
Anyway, door het indelen van de mensen op opleidingsniveau kun je het zien als groepen, en daarom zou je dan categorische toetsen op kunnen uitvoeren (Chi-kwadraat, ANOVA)
Hopelijk helpt dit een beetje?


Ik kan me zo voorstellen dat fetX een tikkie teveel in de stress zit om te reply-en. Maar netjes is het niet inderdaad.
Opleiding laag-midden-hoog kan je wel als continue variabele zien toch?
Opleiding laag-midden-hoog kan je wel als continue variabele zien toch?
Aldus.


Kan ook zijn dat hij (zij) zijn (haar) probleem zelf al op had gelost heeft ondertussen of wegens een andere reden niet meer in dit topic heeft gekeken.quote:Op maandag 21 december 2015 13:04 schreef Z het volgende:
Ik kan me zo voorstellen dat fetX een tikkie teveel in de stress zit om te reply-en. Maar netjes is het niet inderdaad.
Opleiding laag-midden-hoog kan je wel als continue variabele zien toch?
En opleidingsniveau kun je in dit geval niet zien als continue variabele. Je weet niet hoe groot de stapjes zijn tussen iedere categorie. Je weet hooguit dat er een ordening in zit, dus ordinaal meetniveau. Dit is niet genoeg om correlaties mee te berekenen.
de variabele "Aantal jaren opleiding genoten" zou daarentegen wel kunnen


Dan nog kun je even het fatsoen opbrengen om een reactie te plaatsen. Vooral als je opzichtig aan het klunzen bent.


Dan ben ik het niet met je eens, aangezien het m.i. gewoon fout is. Vooral gezien het feit dat je eerder al aangaf dat je een "laag-midden-hoog" variabele beschouwt als een continue variabele, wat ook gewoon fout is. Als je met zulke verkeerde assumpties statistiek gaat beoefenen, ga je toch echt de mist in!quote:Op maandag 21 december 2015 14:48 schreef Z het volgende:
Je hebt een punt, maar ik vind het in sommige gevallen toch niet zo'n probleem.


Hi allemaal,
Na wat feedback van mijn begeleider ben ik mijn analyse (meervoudige regressieanalyse) aan het herschrijven. 1 van de punten die ze opnoemde was dat het verschil tussen de Adjusted R squares die ik heb gevonden, namelijk van .062 (model 1 met controlevariabelen) naar .805 (model 2 met vier onafhankelijke variabelen) aardig onmogelijk is. Na alles opnieuw ingevoerd te hebben kom ik op hetzelfde uit, en snap niet wat de oorzaak hiervan is.
Ik heb nu de variabelen los van elkaar in de regressieanalyse ingevoerd en ben erachter dat de hoge r square change het resultaat is van 2 onafhankelijke variabelen die best hoog met elkaar correleren (α= .645). Heeft iemand een idee wat de oorzaak van deze hoge r square change is en wat ik hieraan kan doen?
Alvast bedankt!
[ Bericht 1% gewijzigd door Bruinvis op 29-12-2015 13:09:43 ]
Na wat feedback van mijn begeleider ben ik mijn analyse (meervoudige regressieanalyse) aan het herschrijven. 1 van de punten die ze opnoemde was dat het verschil tussen de Adjusted R squares die ik heb gevonden, namelijk van .062 (model 1 met controlevariabelen) naar .805 (model 2 met vier onafhankelijke variabelen) aardig onmogelijk is. Na alles opnieuw ingevoerd te hebben kom ik op hetzelfde uit, en snap niet wat de oorzaak hiervan is.
Ik heb nu de variabelen los van elkaar in de regressieanalyse ingevoerd en ben erachter dat de hoge r square change het resultaat is van 2 onafhankelijke variabelen die best hoog met elkaar correleren (α= .645). Heeft iemand een idee wat de oorzaak van deze hoge r square change is en wat ik hieraan kan doen?
Alvast bedankt!
[ Bericht 1% gewijzigd door Bruinvis op 29-12-2015 13:09:43 ]


Klinkt inderdaad zoals Z al aangaf als het probleem van Multicollineariteit.quote:Op dinsdag 29 december 2015 13:04 schreef Bruinvis het volgende:
Hi allemaal,
Na wat feedback van mijn begeleider ben ik mijn analyse (meervoudige regressieanalyse) aan het herschrijven. 1 van de punten die ze opnoemde was dat het verschil tussen de Adjusted R squares die ik heb gevonden, namelijk van .062 (model 1 met controlevariabelen) naar .805 (model 2 met vier onafhankelijke variabelen) aardig onmogelijk is. Na alles opnieuw ingevoerd te hebben kom ik op hetzelfde uit, en snap niet wat de oorzaak hiervan is.
Ik heb nu de variabelen los van elkaar in de regressieanalyse ingevoerd en ben erachter dat de hoge r square change het resultaat is van 2 onafhankelijke variabelen die best hoog met elkaar correleren (α= .645). Heeft iemand een idee wat de oorzaak van deze hoge r square change is en wat ik hieraan kan doen?
Alvast bedankt!
Kijk maar eens naar de formule van hoe de R-squared berekend wordt als je 2 voorspellende variabelen zou hebben:
Deze formule generaliseert ook naar hogere dimensies (dus met 4 voorspellers is het hetzelfde idee). In de formule betekent de r(1,2) de correlatie tussen voorspellende variabele 1 en 2. Als deze correlatie heel klein is, of zelfs 0 (wat dus het geval is als ze onafhankelijk zijn van elkaar) vallen grote delen van de formule weg omdat deze 0 zijn. Maar als de r(1,2) groot is, dan gaat de R squared richting de 1 (en een R-squared van 1 is nooit een goed teken aangezien je data dan perfect voorspeld wordt en dat is niet de bedoeling)
Er zijn verschillende manieren om dit probleem te behandelen, afhankelijk van je kennis en vaardigheid met statistiek. Mensen die daar wat vaardiger in zijn zouden kunnen proberen of een vorm van penalized regression het probleem oplost (Ridge regression bv.) of ipv regressie een andere methode proberen als die past bij de dataset. Beginners zullen moeten proberen om de 2 variabelen die sterk met elkaar correleren, proberen samen te voegen. Eentje van de 2 gewoon niet meenemen is ook een optie, maar ja, dan gooi je dus een hoop informatie weg en ik kan me voorstellen dat het niet leuk is om een onderzoek op te stellen met 4 voorspellers en er vervolgens 1 niet kunnen gebruiken. Andere optie is om het gewoon zo te laten, maar ja dan moet je dus wel uitleggen dat de gevonden R-squared eigenlijk nergens meer op slaat, en waarom.


Bedankt voor jullie reacties! Mijn kennis van statistiek is basis dus ik heb geprobeerd de 2 variabelen samen te voegen, maar dat haalde helaas niks uit qua R-squared. Ik haal daarom toch maar 1 van de 2 variabelen uit de analyse. Idd jammer, maar dan slaat het in ieder geval nog ergens op (hoop ik).
Wat ik dan alleen nog niet begrijp is dat de adjusted r-squared nog steeds naar ,60 stijgt in model 2, terwijl ik geen tekens van multicollineariteit kan ontdekken (VIF waarden rond de 1.0 en onderlinge correlaties tussen de onafhankelijke variabelen zijn niet hoger dan .48).
Ik ben allang blij dat het de r-squared ,80 naar ,60 is gedaald maar toch lijkt dat me nog steeds erg hoog. Hebben jullie een idee of er nog een andere oorzaak kan zijn? Of is dit een acceptabele waarde?
Wat ik dan alleen nog niet begrijp is dat de adjusted r-squared nog steeds naar ,60 stijgt in model 2, terwijl ik geen tekens van multicollineariteit kan ontdekken (VIF waarden rond de 1.0 en onderlinge correlaties tussen de onafhankelijke variabelen zijn niet hoger dan .48).
Ik ben allang blij dat het de r-squared ,80 naar ,60 is gedaald maar toch lijkt dat me nog steeds erg hoog. Hebben jullie een idee of er nog een andere oorzaak kan zijn? Of is dit een acceptabele waarde?


Waarom denk je dat een hoge r-squared slecht is?quote:Op dinsdag 29 december 2015 18:29 schreef Bruinvis het volgende:
Bedankt voor jullie reacties! Mijn kennis van statistiek is basis dus ik heb geprobeerd de 2 variabelen samen te voegen, maar dat haalde helaas niks uit qua R-squared. Ik haal daarom toch maar 1 van de 2 variabelen uit de analyse. Idd jammer, maar dan slaat het in ieder geval nog ergens op (hoop ik).
Wat ik dan alleen nog niet begrijp is dat de adjusted r-squared nog steeds naar ,60 stijgt in model 2, terwijl ik geen tekens van multicollineariteit kan ontdekken (VIF waarden rond de 1.0 en onderlinge correlaties tussen de onafhankelijke variabelen zijn niet hoger dan .48).
Ik ben allang blij dat het de r-squared ,80 naar ,60 is gedaald maar toch lijkt dat me nog steeds erg hoog. Hebben jullie een idee of er nog een andere oorzaak kan zijn? Of is dit een acceptabele waarde?
Wat is eigenlijk hoog?
Het centrale idee bij statistiek is dat al die cijfertjes niet een absoluut natuurkundig gegeven zijn die zomaar uit de lucht komen vallen... ze zijn het resultaat van formules waar weer allemaal andere cijfertjes ingestopt zijn, en die formules zijn ergens, op een gegeven moment, ook maar bedacht door iemand, die er voor koos om er een bepaalde interpretatie aan te geven.
Weet je wat een R-squared is en waar het voor staat?
Dan weet je ook of een R-squared van 0.6 of 0.8 (of wat dan ook) in jou geval hoog of laag is


Als ik het goed heb begrepen staat het percentage van R-squared voor de verklaring van de variantie in de afhankelijke variabele (in mijn geval is de afhankelijke variabele de motivatie om ergens aan mee te doen). Dus de variantie in die motivatie is in mijn geval voor 80 of 60% afhankelijk van de variabelen in mijn model.
Ik vind de r-squared van 0.8 vooral hoog in vergelijking met mijn eerste model, waar alleen de controlevariabelen in zitten en maar 0.06 verklaart. En als ik naar andere onderzoeken kijk, waar ik het mijne op gebaseerd heb, is 80% heel hoog. Maar waardoor het in mijn geval komt (buiten multicollineariteit), dat snap ik dan helaas weer net niet.
[ Bericht 0% gewijzigd door Bruinvis op 29-12-2015 20:49:52 ]
Ik vind de r-squared van 0.8 vooral hoog in vergelijking met mijn eerste model, waar alleen de controlevariabelen in zitten en maar 0.06 verklaart. En als ik naar andere onderzoeken kijk, waar ik het mijne op gebaseerd heb, is 80% heel hoog. Maar waardoor het in mijn geval komt (buiten multicollineariteit), dat snap ik dan helaas weer net niet.
[ Bericht 0% gewijzigd door Bruinvis op 29-12-2015 20:49:52 ]


Klopt.quote:Op dinsdag 29 december 2015 20:19 schreef Bruinvis het volgende:
Als ik het goed heb begrepen staat het percentage van R-squared voor de verklaring van de variantie in de afhankelijke variabele (in mijn geval is de afhankelijke variabele de motivatie om ergens aan mee te doen). Dus de variantie in die motivatie is in mijn geval voor 80 of 60% afhankelijk van de variabelen in mijn model.
Ik vind de r-squared van 0.8 vooral hoog in vergelijking met mijn eerste model, waar alleen de controlevariabelen in zitten en maar 0.06 verklaart. En als ik naar andere onderzoeken kijk, waar ik het mijne op gebaseerd heb, is 80% heel hoog. Maar waardoor het in mijn geval komt (buiten multicollineariteit), dat snap ik dan helaas weer net niet.
En tja, zonder verder zelf de data te bekijken kan ik het verder ook niet beoordelen.