SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Jouw eerdere vier vectoren zijn lineair onafhankelijk en zitten allemaal in de nulruimte. Omdat de nulruimte ook vierdimensionaal is moeten die vier vectoren wel een basis vormen. Maar een basis is nooit uniek. Bijvoorbeeld {(1,0), (0,1)} en {(2,1),(1,2)} zijn al twee verschillende bases van R^2.quote:Op woensdag 11 maart 2015 22:05 schreef Novermars het volgende:
Mathematica geeft trouwens een andere basis van de nulruimte van A aan, namelijk {{-1, 0, 0, 0, 1}, {-1, 0, 0, 1, 0}, {-1, 0, 1, 0, 0}, {-1, 1, 0, 0, 0}}
Ik zou Mathematica vertrouwen, aangezien ik dit uit mijn hoofd heb gedaan. Ik neem aan dat je het antwoord navenant kan aanpassen.
Wat is precies je vraag/opmerking? In de vraag staat al dat het een subspace/deelruimte(?) is, dus per definitie is de constante polynoom f =0 een element van deze subspace.quote:
[..]
En dat doe je omdat f(0)=0? Waardoor de enige 'constante polynoom' f(x)=0 is.
Zo'n vermoeden had ik ook al, maar was verbaasd dat Mathematica met deze vier vectoren kwam. Aangezien ik het even snel uit mijn hoofd had gedaan en ik vrij veel vertrouwen heb in Mathematica, heb ik er dit als kanttekening bij gezet.quote:
[..]
Jouw eerdere vier vectoren zijn lineair onafhankelijk en zitten allemaal in de nulruimte. Omdat de nulruimte ook vierdimensionaal is moeten die vier vectoren wel een basis vormen. Maar een basis is nooit uniek. Bijvoorbeeld {(1,0), (0,1)} en {(2,1),(1,2)} zijn al twee verschillende bases van R^2.
Nou in het algemeen zijn vijfdegraadspolynomen van de vormquote:
[..]
Wat is precies je vraag/opmerking? In de vraag staat al dat het een subspace/deelruimte(?) is, dus per definitie is de constante polynoom f =0 een element van deze subspace.
f(x) = a + bx + ... + f x^5.
Jij neemt in feite direct a=0 en Amoeba viel daarover. Maar omdat elementen in U voldoen aan f(0)=0, weet je dat f(0)=a=0 en dus kan je die constante weglaten. Ik vroeg me af of dat inderdaad de reden is waarom je de a weglaat in je argument.
Oh, op die fiets. Ja, dat is inderdaad de reden dat ik meteen aannam dat a=0. Misschien had ik inderdaad beter met de volledige vorm kunnen beginnen en met het gegeven f(0)=0 kunnen zeggen dat dat a=0 impliceert.quote:
[..]
Nou in het algemeen zijn vijfdegraadspolynomen van de vorm
f(x) = a + bx + ... + f x^5.
Jij neemt in feite direct a=0 en Amoeba viel daarover. Maar omdat elementen in U voldoen aan f(0)=0, weet je dat f(0)=a=0 en dus kan je die constante weglaten. Ik vroeg me af of dat inderdaad de reden is waarom je de a weglaat in je argument.
Dat is inderdaad wat ik bedoel met argument en conclusie omdraaien.quote:
[..]
Nou in het algemeen zijn vijfdegraadspolynomen van de vorm
f(x) = a + bx + ... + f x^5.
Jij neemt in feite direct a=0 en Amoeba viel daarover. Maar omdat elementen in U voldoen aan f(0)=0, weet je dat f(0)=a=0 en dus kan je die constante weglaten. Ik vroeg me af of dat inderdaad de reden is waarom je de a weglaat in je argument.
Fervent tegenstander van het korps lasergamers.
Om nog maar even een vraag te stellen:
Solve the diffusion equation with variable dissipation:
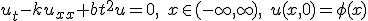
Met b>0.
Solve the diffusion equation with variable dissipation:
Met b>0.
Zie hier.quote:
Om nog maar even een vraag te stellen:
Solve the diffusion equation with variable dissipation:
Met b>0.
Ik moet het vectorveld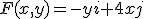 
waarbij i en j de cartesische basisvectoren zijn, transformeren naar poolcoördinaten. Ik weet dat 
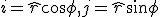, maar wat moet ik met de (x,y)? Alvast dank!
Dat klopt alvast niet. Een vector is geen scalar ...quote:
Ik moet het vectorveld
Het lijkt me de bedoeling dat je F uitdrukt in i en j als functie van de poolcoördinaten (r, φ).quote:maar wat moet ik met de (x,y)? Alvast dank!
Bedankt! Ik vind het best verwarrend dat ze r en r dakje beide gebruiken, komt het daardoor?quote:
[..]
Dat klopt alvast niet. Een vector is geen scalar ...
[..]
Het lijkt me de bedoeling dat je F uitdrukt in i en j als functie van de poolcoördinaten (r, φ).
Zou iemand me verder kunnen helpen? Ik snap het niet zo goed en mijn boek zegt niks over transformaties.
Behalve:
Meer aanknopingen of een (link naar een) vergelijkbaar voorbeeld zijn erg welkom.
Ah, zo. Verwarrend inderdaad, r is een scalar, r een radiusvector en r̂ een unit radius vector. Zie hier. Je uitdrukking voor φ̂ klopt trouwens niet. Differentiëren vanquote:
[..]
Bedankt! Ik vind het best verwarrend dat ze r en r dakje beide gebruiken, komt het daardoor?
Zou iemand me verder kunnen helpen? Ik snap het niet zo goed en mijn boek zegt niks over transformaties.
Behalve: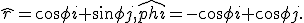
Meer aanknopingen of een (link naar een) vergelijkbaar voorbeeld zijn erg welkom.
naar φ levert een vector op die een kwart slag in tegenwijzerzin is gedraaid en daarmee hebben we
[ Bericht 9% gewijzigd door Riparius op 19-03-2015 16:45:39 ]
Je hebt gelijk, dat was een lelijke overtypfout. Ik heb nu met een trucje de basisvectortransformatie geïnverteerd en x en y naar poolcoördinaten omgeschreven. Het is aan het lukken, hoera!quote:
[..]
Ah, zo. Verwarrend inderdaad, r is een scalar, r een radiusvector en r̂ een unit radius vector. Zie hier. Je uitdrukking voor φ̂ klopt trouwens niet. Differentiëren van
naar φ levert een vector op die een kwart slag in tegenwijzerzin is gedraaid en daarmee hebben we
Omdat sin^2(x)+cos^2(x) = 1 voor alle x.quote:
Dit kun je inzien door de eenheidscirkel te bekijken:
Voor ieder punt op de eenheidscirkel geldt dat de x-coordinaat wordt gegeven door cos(t), de y-coordinaat wordt gegeven door sin(t). Met de stelling van Pythagoras:
x^2 + y^2 = r^2
met r de straal van de cirkel. Maar je weet dat de straal van de eenheidscirkel 1 is (daarom heet het de eenheidscirkel). Als je in de stelling van Pythagoras dan de x-coordinaat, de y-coordinaat en de straal invult krijg je de formule die je nodig hebt.
Dank jequote:Op dinsdag 24 maart 2015 20:22 schreef Alrac4 het volgende:
[..]
Omdat sin^2(x)+cos^2(x) = 1 voor alle x
Wie kan helpen met de volgende vragen?
A) Bereken de onbepaalde integraal:
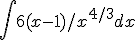
B) Bereken de onbepaalde integraal:
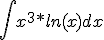
[ Bericht 17% gewijzigd door #ANONIEM op 25-03-2015 12:10:20 ]
A) Bereken de onbepaalde integraal:
B) Bereken de onbepaalde integraal:
[ Bericht 17% gewijzigd door #ANONIEM op 25-03-2015 12:10:20 ]
A) Herschrijf de integrand alsquote:
Wie kan helpen met de volgende vragen?
A) Bereken de onbepaalde integraal:
B) Bereken de onbepaalde integraal:
B) Gebruik partiële integratie. Zie ook hier.
|| FOK!Stok || tatatatatataatatatattaaaaapiediedieuwtididipieuwpidibididi She said I'll throw myself away pididididum They're just photos after all! || Den Helder || Winnaar VBL Wijndal-award 2020: beste AZ-user! || Mijn concertstatistieken ||
Op een (x,y) vlak, teken de vergelijking 200x+ 300y=q, waarbij je q zelf mag kiezen.quote:
Op Voor elke q heb je dan een iso-winstlijn.
Dan heb ik nog een vraag, namelijk, stel ik wil sin(t)=(1/2) oplossen, waarom is 1+(2/3)pi +2kpi geen oplossing? (Als je de oplossingen afleest van de eenheidscirkel)quote:
[..]
Om te beginnen moet je de sinus en cosinus van een aantal 'standaardhoeken', namelijk 0, 30, 45, 60 en 90 graden, gewoon uit het blote hoofd kennen. Daar is trouwens een eenvoudig ezelsbruggetje voor: de sinus van de genoemde hoeken is namelijk resp.
½√0, ½√1, ½√2, ½√3, ½√4
en dus
0, ½, ½√2, ½√3, 1
en de cosinus van de genoemde hoeken krijg je achtereenvolgens door hetzelfde rijtje van rechts naar links op te schrijven.
Met behulp van de definitie van de sinus en de cosinus aan de hand van de eenheidscirkel (zie ook hier) zie je gemakkelijk dat tegengestelde (rotatie)hoeken tegengestelde sinussen hebben, dus
sin(−α) = −sin α
maar dezelfde cosinus, dus
cos(−α) = cos α
Goed, als je nu bedenkt dat sin 45° = ½√2 en dat 45° overeenkomt met ¼π radialen, dus sin(¼π) = ½√2, dan weet je ook dat sin(−¼π) = −½√2.
Nu is het ook nog zo dat supplementaire (rotatie)hoeken dezelfde sinus hebben, dus
sin(π−α) = sin α
maar een tegengestelde cosinus, dus
cos(π−α) = −cos α
Aangezien de sinus van −¼π gelijk is aan −½√2 is de sinus van π − (−¼π) = (5/4)·π dus eveneens gelijk aan −½√2.
Tot slot, de sinus en de cosinus zijn periodieke functies met een periode 2π, dus als complete oplossing van de vergelijking
sin x = −½√2
krijg je zo
x = −¼π + 2kπ ∨ x = (5/4)·π + 2kπ, k ∈ Z
Als je 2π optelt bij −¼π dan krijgen we (7/4)·π, zodat we dus de complete oplossing evengoed als
x = (7/4)·π + 2kπ ∨ x = (5/4)·π + 2kπ, k ∈ Z
kunnen schrijven.
Nu hangt het verder van het vraagstuk af aan welke eventuele andere voorwaarde(n) de gevraagde oplossing(en) moet(en) voldoen, maar aangezien je niet duidelijk maakt wat in je opgave met B wordt bedoeld kan ik hier geen antwoord op geven.
De oplossingen moeten in ieder geval rationale veelvouden zijn van π omdat sin(⅙π) = ½, dus de waarde die jij geeft is zeker geen oplossing. Of misschien bedoel je (5/3)·π + 2kπ, k ∈ Z, maar ook dat is geen oplossing van je vergelijking. Immers, je hebt π < (5/3)·π < 2π, dus als je het startpunt (1; 0) om de oorsprong roteert over een hoek van (5/3)·π radialen dan kom je uit op een punt onder de x-as, en daar is de y-coördinaat, en dus ook de sinus, negatief, zodat het evident is dat de sinus van (5/3)·π + 2kπ, k ∈ Z negatief moet zijn en niet ½ kan zijn.quote:
[..]
Dan heb ik nog een vraag, namelijk, stel ik wil sin(t)=(1/2) oplossen, waarom is 1+(2/3)pi +2kpi geen oplossing? (Als je de oplossingen afleest van de eenheidscirkel)
Kijk nog eens naar het volgende plaatje:
We weten dat sin 30° = ½ en dat 30° gelijk is aan 1/6 deel van een gestrekte hoek en daarmee overeenkomt met π/6 rad zodat sin(⅙π) = ½. En omdat supplementaire hoeken dezelfde sinus hebben is dus ook sin 150° = ½ oftewel sin(⅚π) = ½.
Dit kun je ook in het plaatje aflezen, want driehoek OPQ in het tweede kwadrant is congruent met de gestreept getekende driehoek in het eerste kwadrant. Bedenk hierbij dat de sinus van een gegeven (rotatie)hoek per definitie de y-coördinaat is van het beeld van het startpunt (1; 0) bij een rotatie om de oorsprong over de gegeven hoek.
Verder komen we altijd weer op dezelfde punten op de eenheidscirkel uit na een extra rotatie om de oorsprong over een willekeurig aantal gehele slagen in tegenwijzerzin (positief) of in wijzerzin (negatief). Een volledige rotatie om de oorsprong komt overeen met een rotatie over 360° oftewel 2π radialen, en als complete oplossing van de vergelijking sin(t) = ½ krijgen we dus:
t = ⅙π + 2kπ ∨ t = ⅚π + 2kπ, k ∈ Z
[ Bericht 0% gewijzigd door Riparius op 02-04-2015 20:58:40 ]
Ik ben bezig met het vereenvoudigen van een som, alleen snap ik 1 stap niet. Kan iemand me hieruit helpen?
-2500e^-0,5t x 2(1+20e^-0,5t) x 20e^-0,5t x -0,5
Wordt
50000e^-0,5t x e^-0,5t x (1+20e^-0,5t)
Ik snap niet hoe ze bij dat laatste deel aan die e^-0,5t komen
-2500e^-0,5t x 2(1+20e^-0,5t) x 20e^-0,5t x -0,5
Wordt
50000e^-0,5t x e^-0,5t x (1+20e^-0,5t)
Ik snap niet hoe ze bij dat laatste deel aan die e^-0,5t komen
