[Bèta wiskunde] Huiswerk- en vragentopic

Index

» school, studie en onderwijs

actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
pi_136072339
Ik snap niet hoe je bij die laatste formule komt.
pi_136072469
quote:
0s.gif Op dinsdag 28 januari 2014 21:50 schreef thabit het volgende:
Ik snap niet hoe je bij die laatste formule komt.
Ja die is gegarandeerd fout. Ik weet niet hoe ik de coëfficiënten van mijn expansie terugkrijg.
pi_136072562
Dus...

ak = 1, 3, 6*3, 9*6*3, 12*9*6*3...
pi_136072594
Er staat ck = -ck-3/k, dus er zal iets met faculteiten in de noemers moeten komen.
pi_136072758
quote:
0s.gif Op dinsdag 28 januari 2014 21:55 schreef thabit het volgende:
Er staat ck = -ck-3/k, dus er zal iets met faculteiten in de noemers moeten komen.
Ja, dat wil zeggen:

y(x) = \sum_{k=0}^{\infty}\frac{x^{3k}(-1)^k}{a_k}

met

quote:
2s.gif Op dinsdag 28 januari 2014 21:54 schreef Amoeba het volgende:

ak = 1, 3, 6*3, 9*6*3, 12*9*6*3...
pi_136072799
Maar ik weet niet hoe ik dat rijtje bouw met faculteiten.
pi_136072918
Nou, in elk van die factoren zit telkens een factor 3. Haal die er eerst maar eens uit.
pi_136073036
quote:
0s.gif Op dinsdag 28 januari 2014 22:00 schreef thabit het volgende:
Nou, in elk van die factoren zit telkens een factor 3. Haal die er eerst maar eens uit.
Maar niet in de eerste, die is namelijk 1. :?
pi_136073066
quote:
2s.gif Op dinsdag 28 januari 2014 22:02 schreef Amoeba het volgende:

[..]

Maar niet in de eerste, die is namelijk 1. :?
1 is het lege product, dus die heeft geen factoren.
pi_136073270
quote:
0s.gif Op dinsdag 28 januari 2014 22:02 schreef thabit het volgende:

[..]

1 is het lege product, dus die heeft geen factoren.
Okay.

Maar mijn berekening tot dusverre,

y(x) = c_0 \sum_{k=0}^{\infty}\frac{x^{3k}(-1)^k}{a_k}

met a_k = \{1, 3\cdot1, 6\cdot3\cdot1, 9\cdot6\cdot3\cdot1....}, c_0 \in \mathbb{R}

is juist?

Mijn vraag komt er echt op neer wat (ak) in gesloten vorm is..

[ Bericht 0% gewijzigd door #ANONIEM op 28-01-2014 22:08:36 ]
pi_136073617
a4 is bijvoorbeeld 12 * 9 * 6 * 3. Nu is 12=3*4, 9=3*3, 6=3*2, en 3=3*1.
pi_136073841
1
3 1
3 3 2 1
4 3 3 3 3 2 1

dus uhm

a_k = (k+1)! \cdot 3^{k} ?

[ Bericht 2% gewijzigd door #ANONIEM op 28-01-2014 22:20:29 ]
pi_136073921
Waarom (k+1)! ?
pi_136073934
Meh, dit gaat mis. Even kijken. :')
pi_136074240
Eerste correctie bleek goed denk ik.

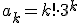
a_k = k!\cdot3^k


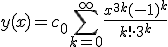
=> y(x) = c_0 \sum_{k=0}^{\infty}\frac{x^{3k}(-1)^k}{k!\cdot3^k}

Volgens Cauchy's Ratio Test convergeert y(x) op heel R, en dan nu die gesloten uitdrukking nog. Left for tomorrow I suppose.

Thabit, mijn dank. :Y

Ik ben natuurlijk vergeten dat c0 ongelijk 0 is, anders is alles flauw.

[ Bericht 33% gewijzigd door #ANONIEM op 28-01-2014 22:37:57 ]
pi_136075395
quote:
2s.gif Op dinsdag 28 januari 2014 22:21 schreef Amoeba het volgende:
Eerste correctie bleek goed denk ik.

a_k = k!\cdot3^k
Jij bedoelt met ak iets anders dan in de oorspronkelijke opgave, en dat moet je natuurlijk niet doen. De oplossing van je DV is uiteraard y(x) = e−x³/3, dus het is gemakkelijk na te gaan wat de coëfficiënten van je machtreeks zouden moeten zijn.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_136096929
http://imgur.com/CS9i9Y4
Hoe bewijs ik dat de functierij niet uniform convergeert bij b)? De puntsgewijze functie is 0 voor alle x in R, dus ik kan niet het argument gebruiken dat de limiet functie niet continu is... Ik zat zelf verder nog te denken aan de supremum norm, maar dan lukt de maximale waarde bepalen niet...
pi_136103793
quote:
0s.gif Op woensdag 29 januari 2014 15:43 schreef spacer730 het volgende:
http://imgur.com/CS9i9Y4
Hoe bewijs ik dat de functierij niet uniform convergeert bij b)? De puntsgewijze functie is 0 voor alle x in R, dus ik kan niet het argument gebruiken dat de limiet functie niet continu is... Ik zat zelf verder nog te denken aan de supremum norm, maar dan lukt de maximale waarde bepalen niet...
Het gaat mis rond het punt 0. Kijk eens wat er gebeurt als je bijvoorbeeld x=1/n neemt.
pi_136105458
quote:
0s.gif Op woensdag 29 januari 2014 18:28 schreef thenxero het volgende:

[..]

Het gaat mis rond het punt 0. Kijk eens wat er gebeurt als je bijvoorbeeld x=1/n neemt.
Als x=1/n, dan gaat de functierij voor n->oneindig dus naar sin(1)/e, dus niet continu dus geen uniforme convergentie? Dan zou de puntsgewijze limietfunctie dus ook niet 0 zijn voor alle x
pi_136108129
quote:
0s.gif Op woensdag 29 januari 2014 19:05 schreef spacer730 het volgende:

[..]

Als x=1/n, dan gaat de functierij voor n->oneindig dus naar sin(1)/e, dus niet continu dus geen uniforme convergentie? Dan zou de puntsgewijze limietfunctie dus ook niet 0 zijn voor alle x
Je moet gewoon netjes de definities toepassen van puntsgewijze convergentie en uniforme convergentie. Puntsgewijze convergentie van je functierij {fn} naar een functie f* op R betekent dat je voor elke x ∈ R hebt

limn→∞ fn(x) = f*(x)

Bij a) word je gevraagd na te gaan dat dit inderdaad het geval is en f* te bepalen.

Uniforme convergentie van je functierij {fn} naar de bij a) bepaalde functie f* op R zou inhouden dat er voor elke ε > 0 een N ∈ N bestaat zodanig dat voor elke n > N en elke x ∈ R geldt

| fn(x) − f*(x) | < ε

Bij b) word je gevraagd aan te tonen dat dit niet het geval is voor jouw functierij {fn} en de bij a) bepaalde functie f*.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_136108826
Voor de liefhebbers, op Coursera is een course 'Functional Analysis' begonnen. https://class.coursera.org/functionalanalysis-001

Het begint nog redelijk simpel, zeker de filmpjes. Maar de supplementaire PDF is toch wel redelijk pittig.
pi_136111447
quote:
0s.gif Op woensdag 29 januari 2014 20:04 schreef Novermars het volgende:
Voor de liefhebbers, op Coursera is een course 'Functional Analysis' begonnen. https://class.coursera.org/functionalanalysis-001

Het begint nog redelijk simpel, zeker de filmpjes. Maar de supplementaire PDF is toch wel redelijk pittig.
Fijne site, maar niet heus. Ik zie niet in waarom zoiets weggestopt moet worden achter een login, en mijn browser loopt ook nog eens vast op een script op de site wanneer ik een lijst probeer op te vragen van het cursusaanbod.
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_136116821
quote:
0s.gif Op woensdag 29 januari 2014 20:54 schreef Riparius het volgende:

[..]

Fijne site, maar niet heus. Ik zie niet in waarom zoiets weggestopt moet worden achter een login, en mijn browser loopt ook nog eens vast op een script op de site wanneer ik een lijst probeer op te vragen van het cursusaanbod.
https://www.dropbox.com/s(...)alysis-week01-V2.pdf

Syllabus:
Week 1: Topology; continuity and convergence of a sequence in a topological space.
Week 2: Metric and normed spaces; completeness
Week 3: Banach spaces; linear continuous functions; weak topology
Week 4: Hilbert spaces; The Riesz representation theorem
Week 5: The Lax-Milgram Lemma
Week 6: Lp spaces; Fischer-Riesz
Week 7: Sobolev spaces
Week 8: Use of functional analysis for Partial Differential Equations
pi_136140427
Haha, ik droomde vannacht dat Riparius weer een uitlegpost had gemaakt (of twee eigenlijk, want het paste niet in een post). Ik heb zo tentamen, zal daar wel door komen denk ik :P
pi_136141323
quote:
0s.gif Op woensdag 29 januari 2014 19:05 schreef spacer730 het volgende:

[..]

Als x=1/n, dan gaat de functierij voor n->oneindig dus naar sin(1)/e, dus niet continu dus geen uniforme convergentie? Dan zou de puntsgewijze limietfunctie dus ook niet 0 zijn voor alle x
Zoiets, maar dit is nog wat te vaag (en ook twijfelachtig, de puntsgewijze limiet is overal 0 dus je hebt wel continuïteit). Mijn punt was eigenlijk: voordat je een bewijs gaat opstellen wil je eerst kijken naar wat er (in dit geval) misgaat. Als je eenmaal geïdentificeerd hebt dat het rond x=0 misgaat (wat je dus kan inzien door x=1/n in te vullen), kan je een rigoureus bewijs geven.

Neem epsilon = sin(1)/e. Laat N in N willekeurig zijn. Neem n=N en x=1/n, dan |f_n(x)-0|>= epsilon. Klaar.
actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
[Bèta wiskunde] Huiswerk- en vragentopic
Index

» school, studie en onderwijs

Forum Opties
Forumhop:
Hop naar:
(afkorting, bv 'KLB')