[Bèta wiskunde] Huiswerk- en vragentopic

quote:

Op zondag 11 november 2012 16:34 schreef Amoeba het volgende:

[..]

Strikt genomen is je opgave niet op te lossen, omdat het geen vergelijking is. Waaraan moet dit gelijk zijn?

Het kan ook een simpele oefening zijn in het herleiden van een veelterm. In ieder geval is het geen 'som' want dat is de uitkomst van een optelling. Platina maakt de verwarring alleen maar groter door aan te nemen dat het om een vergelijking gaat, maar dat blijkt nergens uit (en de letter a wordt gewoonlijk voor een constante of bekende grootheid gebruikt, niet voor een variabele of onbekende grootheid).

quote:

Op zondag 11 november 2012 17:40 schreef Riparius het volgende:

[..]

Het kan ook een simpele oefening zijn in het herleiden van een veelterm. In ieder geval is het geen 'som' want dat is de uitkomst van een optelling. Platina maakt de verwarring alleen maar groter door aan te nemen dat het om een vergelijking gaat, maar dat blijkt nergens uit (en de letter a wordt gewoonlijk voor een constante of bekende grootheid gebruikt, niet voor een variabele of onbekende grootheid).

Uiteraard. Inderdaad wordt in de methode Getal & Ruimte (vooral in de lagere klassen) vaak de opgave 'herleid de volgende veeltermen' gegeven, ter oefening.

quote:

Op zondag 11 november 2012 15:38 schreef christiado het volgende:
Hey iedereen,

Kan iemand mij helpen met het oplossen van een som? Het gaat hier om
de rekenen met letters, maar ik kom er helaas niet uit.

(8-5)(7a-3) +7a +3

T zal heel fijn zijn als iemand hiermee kan helpen.

Het is handig de merkwaardige producten uit je hoofd te kennen:

(a+b)² = a² +2ab + b²
(a-b)(a+b) = a² - b²
(a+b)(c+d) = ac + bc + ad + bd

Dit is in feite 'rekenen met letters'. Echter nu substitueer je voor a, b, c en d de gegeven waarden. bijvoorbeeld mag je substitueren:

b = 7a of b = 3 of b = sin(a) of b = 5000sec(a).

Het beste voorbeeld is het 'pijltjes' voorbeeld. Je vermenigvuldigt alles tussen de eerste haakjes met alles tussen de tweede haakjes, dus a met c en d en b met c en d. Stel dat je hebt (a + b + c)(d+e+f), wat krijg je dan? Als je weet dat hiervoor precies hetzelfde geldt?

[ Bericht 0% gewijzigd door Amoeba op 11-11-2012 18:16:09 ]

quote:

Op zondag 11 november 2012 18:02 schreef Amoeba het volgende:

Het is handig de opmerkelijke producten uit je hoofd te kennen:

Ja. Moet je het wel zelf goed doen natuurlijk ...

Hier staat een gangbaar (?) lijstje. Het zijn trouwens merkwaardige producten, i.e. producten die het merken (onthouden) waard zijn.

quote:

Op zondag 11 november 2012 18:12 schreef Riparius het volgende:

[..]

Ja. Moet je het wel zelf goed doen natuurlijk ...

Hier staat een gangbaar (?) lijstje.

Wat doe ik fout dan

Ik kan mezelf even niet betrappen op het geven van onjuiste vergelijkingen. En dat laatste is juist. Aangepast.

quote:

Op zondag 11 november 2012 18:13 schreef Amoeba het volgende:

[..]

Wat doe ik fout dan

Ik kan mezelf even niet betrappen op het geven van onjuiste vergelijkingen. En dat laatste is juist. Aangepast.

Minteken bij (a+b)(a-b)

quote:

Op zondag 11 november 2012 18:14 schreef Janneke141 het volgende:

[..]

Minteken bij (a+b)(a-b)

Oja, kut

Ik heb even een vraagje. Mijn boek stelt dat uit de formule van Taylor (Taylorreeks?) de formule van Maclaurin volgt. Uiteraard zonder bewijs. Nu ga ik het bewijs zelf nog even bestuderen wanneer ik tijd heb, maar ik heb wel een vraag betreffende het bewijs van afgeleide functies.

Ik heb met de formule van Maclaurin aan moeten tonen dat f(x) = sin(x) = x - x^3/3! + x^5/5! ... allemaal prima.
Evenzo voor g(x) = cos(x)

Nu moet ik aantonen dat f'(x) = g(x), uitgaande van de 'bewezen' reeksontwikkelingen. En daarna nog dat g'(x) = -f(x). Hoe pak ik dit aan?

Er is een stelling die zegt dat je onder bepaalde voorwaarden een oneindige som termgewijs mag differentiëren. In dit geval mag dat.

Dan zal je zien dat als je de reeksontwikkeling van een sinus differentieert, de reeksontwikkeling van de cosinus krijgt.

Een Maclaurinreeks is gewoon een Taylorreeks die je ontwikkelt in 0, dus daar valt ook weinig aan te bewijzen.

quote:

Op zondag 11 november 2012 19:25 schreef thenxero het volgende:
Er is een stelling die zegt dat je onder bepaalde voorwaarden een oneindige som termgewijs mag differentiëren. In dit geval mag dat.

Dan zal je zien dat als je de reeksontwikkeling van een sinus differentieert, de reeksontwikkeling van de cosinus krijgt.

Een Maclaurinreeks is gewoon een Taylorreeks die je ontwikkelt in 0, dus daar valt ook weinig aan te bewijzen.

Volgens mij geldt dat niet alleen voor een oneindige som.. Maar bedankt. Zag even zo niet direct wat ze bedoelden.

quote:

Op zondag 11 november 2012 19:30 schreef Amoeba het volgende:

[..]

Volgens mij geldt dat niet alleen voor een oneindige som.. Maar bedankt. Zag even zo niet direct wat ze bedoelden.

Voor een eindige som geldt het altijd. Maar met oneindige sommen kan het misgaan. Daar zit nog een hele hoop analyse achter als je wil weten hoe dat precies zit.

quote:

Op zondag 11 november 2012 19:21 schreef Amoeba het volgende:
Ik heb even een vraagje. Mijn boek stelt dat uit de formule van Taylor (Taylorreeks?) de formule van Maclaurin volgt. Uiteraard zonder bewijs. Nu ga ik het bewijs zelf nog even bestuderen wanneer ik tijd heb, maar ik heb wel een vraag betreffende het bewijs van afgeleide functies.

Een Taylor-reeks is een reeksontwikkeling van een functie f(x) rond een punt x = a, zodat je f(x) uitdrukt als een (convergente) oneindige machtreeks waarvan de termen machten van (x-a) zijn. Een MacLaurin-reeks is niets anders dan een speciaal geval van de Taylorreeks voor a = 0. Daar is dan verder weinig aan te bewijzen.

quote:

Ik heb met de formule van Maclaurin aan moeten tonen dat f(x) = sin(x) = x - x^3/3! + x^5/5! ... allemaal prima.
Evenzo voor g(x) = cos(x)

Nu moet ik aantonen dat f'(x) = g(x), uitgaande van de 'bewezen' reeksontwikkelingen. En daarna nog dat g'(x) = -f(x). Hoe pak ik dit aan?

Het idee is dat je de reeksen 'termsgewijs' mag differentiëren, net zoals je een polynoom in x termsgewijs kunt differentiëren. Uiteraard moet dan wel eerst zijn aangetoond onder welke voorwaarden dit mag. Het omgekeerde kan ook, je kunt convergente reeksen (alweer: onder bepaalde voorwaarden) termsgewijs primitiveren. Een (eenvoudig) voorbeeld: je weet dat de som (limiet) van een convergente meetkundige reeks met eerste term a en reden r gelijk is aan a/(1-r). Zo heb je dus bijvoorbeeld:

1/(1 + x) = 1 - x + x² - x³ + .... (|x| < 1)

Primitiveren geeft dan:

ln(1 + x) = x - x²/2 + x³/3 - x⁴/4 + ...

Merk op dat er geen constante bij komt, aangezien we voor x = 0 hebben ln(1) = 0. Dit is de bekende Mercator reeks, gepubliceerd in 1668 door Nicholas Mercator, niet te verwarren met (en geen familie van) de Vlaamse cartograaf Gerard Mercator.

Ik doelde meer op het bewijs van de Maclaurinreeks als zijnde het bewijs van de Taylorreeks. Ik heb wel door dat de Maclaurinreeks niets anders is dan de Taylorreeks voor a = 0, maar verder is het bewijs van de Taylorreeks niet gegeven. Maar dat zoek ik nog wel uit.

Dank allen. En geef maar toe dat je met opzet over een man genaamd Mercator begon. Maar ik moet huiswerk maken, dus heb echt geen tijd om erop in te gaan.

quote:

Op zondag 11 november 2012 19:52 schreef Amoeba het volgende:
Ik doelde meer op het bewijs van de Maclaurinreeks als zijnde het bewijs van de Taylorreeks. Ik heb wel door dat de Maclaurinreeks niets anders is dan de Taylorreeks voor a = 0, maar verder is het bewijs van de Taylorreeks niet gegeven. Maar dat zoek ik nog wel uit.

Bedenk wel dat je voor de herleiding van de reeksen voor sin x en cos x niet gebruik mag maken van de afgeleiden van deze functies en dan vervolgens deze reeksontwikkelingen doodleuk gebruiken om te 'bewijzen' dat d(sin x)/dx = cos x en d(cos x)/dx = -sin x, want dan begeef je je in een cirkelredenering (no pun intended). Het is wat anders als je sin x en cos x definieert aan de hand van hun reeksontwikkelingen, maar dan nog moet je bewijzen dat de reeksen convergent zijn voor elke reële x en bewijzen dat 'termsgewijs' differentiëren hier überhaupt toelaatbaar is. Welk boek gebruik je als ik vragen mag?

quote:

Dank allen. En geef maar toe dat je met opzet over een man genaamd Mercator begon. Maar ik moet huiswerk maken, dus heb echt geen tijd om erop in te gaan. [ afbeelding ]

Je hoeft er ook niet op in te gaan, het was alleen een voorbeeld om te laten zien wat je met 'termsgewijs' differentiëren of primitiveren van een reeksontwikkeling kunt doen. En ja, vind je het gek dat ik bij jou steeds aan Mercator moet denken?

quote:

Op zondag 11 november 2012 20:08 schreef Riparius het volgende:
Bedenk wel dat je voor de herleiding van de reeksen voor sin x en cos x niet gebruik mag maken van de afgeleiden van deze functies en dan vervolgens deze reeksontwikkelingen gebruiken om te 'bewijzen' dat d(sin x)/dx = cos x en d(cos x)/dx = -sin x, want dan begeef je je in een cirkelredenatie (no pun intended). Het is wat anders als je sin x en cos x definieert aan de hand van hun reeksontwikkelingen, maar dan nog moet je bewijzen dat de reeksen convergent zijn voor elke reële x en bewijzen dat 'termsgewijs' differentiëren hier überhaupt toelaatbaar is. Welk boek gebruik je als ik vragen mag?

Wiskunde D. Getal en Ruimte, deel 3. Hoofdstuk 12, pagina 136-137. Hoofdstuk heet 'Complexe getallen gebruiken'. De paragraaf behandelt de formule van Euler.

Ik heb dit gedaan:

Eerst heb ik aangetoond dat met behulp van de Taylorreeks dat sin(x) = x-x^3/3! + x^5/5! - x^7/7! + x^9/9!....

En dat cos(x) = 1-x^2/2!+x^4/4!+x^6/6! etc.

Daarna heb ik de afgeleide van de Taylorreeks van sin(x) genomen, en ja, daarvoor heb ik eerst sin(x) moeten differentiëren naar cos(x) om tot de conclusie te komen dat sin(x) gelijk is aan de Taylorreeks. Daarmee heb ik dus in feite helemaal niets bewezen. Dus dit is een cirkelredenatie.

Toch is dit volgens de uitwerkingen wel correct, deze zijn hier te vinden. Opgave 2.

Zal dinsdag eens slim gaan doen en dit aankaarten.

quote:

Op zondag 11 november 2012 20:08 schreef Riparius het volgende:
Je hoeft er ook niet op in te gaan, het was alleen een voorbeeld om te laten zien wat je met 'termsgewijs' differentiëren of primitiveren van een reeksontwikkeling kunt doen. En ja, vind je het gek dat ik bij jou steeds aan Mercator moet denken?

Dat weet ik. Ik hoop dat jij ook nog weet dat ik graag tot midden in de nacht bezig ben met interessante wiskunde. Volgens mij hebben we dat wel eens ooit besproken. En nee hoor, je 'humor' bevalt me wel.

Ik kan me deze post trouwens nog wel herinneren. Misschien jij ook?

quote:

Op zondag 10 juni 2012 18:35 schreef Amoeba het volgende:
Je bent wel leerzaam trouwens, die anekdotes over de geschiedenis van de wiskunde zijn zeer interessant.

[ Bericht 5% gewijzigd door Amoeba op 11-11-2012 20:22:36 ]

quote:

Op zondag 11 november 2012 20:17 schreef Amoeba het volgende:

[..]

Wiskunde D. Getal en Ruimte, deel 3. Hoofdstuk 12, pagina 136-137. Hoofdstuk heet 'Complexe getallen gebruiken'. De paragraaf behandelt de formule van Euler.

Ik heb dit gedaan:

Eerst heb ik aangetoond dat met behulp van de Taylorreeks dat sin(x) = x-x^3/3! + x^5/5! - x^7/7! + x^9/9!....

En dat cos(x) = 1-x^2/2!+x^4/4!+x^6/6! etc.

Daarna heb ik de afgeleide van de Taylorreeks van sin(x) genomen, en ja, daarvoor heb ik eerst sin(x) moeten differentiëren naar cos(x) om tot de conclusie te komen dat sin(x) gelijk is aan de Taylorreeks. Daarmee heb ik dus in feite helemaal niets bewezen. Dus dit is een cirkelredenatie.

Inderdaad, ik ben blij dat je het probleem ook ziet. Maar veel schrijvers van leerboeken kennelijk niet, of ze zien het wel en hopen dat de studenten het niet in de gaten hebben. Maar het blijft slechte didactiek (en slechte wiskunde). Hetzelfde geldt voor de manier waarop de formule van Euler vaak in leerboeken en cursussen wordt geïntroduceerd.

quote:

Toch is dit volgens de uitwerkingen wel correct, deze zijn hier te vinden. Opgave 2.

Zal dinsdag eens slim gaan doen en dit aankaarten.

quote:

Op zondag 11 november 2012 20:17 schreef Amoeba het volgende:

Ik kan me deze post trouwens nog wel herinneren. Misschien jij ook?

[..]

Uiteraard, het zou niet best zijn als ik me mijn eigen posts na een paar maanden al niet meer zou herinneren. Grappig trouwens dat ik daar Jacob Bernoulli noem, ik zat net wat briefwisselingen tussen Leibniz en de broers Jacob en Johann Bernoulli te lezen waarin het zogeheten Bazel-probleem aan de orde komt. Daar zie je ook mooi hoe nonchalant men toen omging met het manipuleren van reeksen, waaronder de Mercator reeks, die op een bepaalde manier een rol speelde bij het Bazel-probleem. Maar daarover misschien een andere keer meer, omdat je kennelijk denkt dat je uit je boek meer leert ...

quote:

Op zondag 11 november 2012 20:37 schreef Riparius het volgende:

[..]

Uiteraard, het zou niet best zijn als ik me mijn eigen posts na een paar maanden al niet meer zou herinneren. Grappig trouwens dat ik daar Jacob Bernoulli noem, ik zat net wat briefwisselingen tussen Leibniz en de broers Jacob en Johann Bernoulli te lezen waarin het zogeheten Bazel-probleem aan de orde komt. Daar zie je ook mooi hoe nonchalant men toen omging met het manipuleren van reeksen, waaronder de Mercator reeks, die op een bepaalde manier een rol speelde bij het Bazel-probleem. Maar daarover misschien een andere keer meer, omdat je kennelijk denkt dat je uit je boek meer leert ...

Waar staat dat? Ik stel zelfs nog dat je heel leerzaam bent in mijn eigen quote. Ik krijg op m'n donder als ik die opgaven niet af heb. Kan ik er wat aan doen dat het boek fouten maakt..

Maar, hoe zou je dan bewijzen dat de [sin(x)]' = cos(x) met behulp van reeksen?

Net als opgave 9b.

druk sin(x) uit in e^ix en e^-ix
Waarbij je bij a aan moest toen dat:



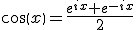
Krijg je dit als uitwerking.



Vond ik mijn uitwerking met behulp van de integraalrekening (want de primitieve van cos(x) is sin(x)) toch een stuk eleganter. Ik vrees dat je toch wat 'leerzamer' bent.

quote:

Op zondag 11 november 2012 21:21 schreef Amoeba het volgende:

[..]

Waar staat dat? Ik stel zelfs nog dat je heel leerzaam bent in mijn eigen quote. Ik krijg op m'n donder als ik die opgaven niet af heb. Kan ik er wat aan doen dat het boek fouten maakt..

Maar, hoe zou je dan bewijzen dat de [sin(x)]' = cos(x) met behulp van reeksen?

Ha, dat is wel een leuke opgave. Je kan het doen door de volgende differentiaalvergelijking te beschouwen

.

(Dat is niet vreemd want je weet stiekem al dat sinus en cosinus aan deze DV voldoen, maar dat moet je direct weer vergeten want je wil nog laten zien dat sin' =cos)

Als je de volgende randvoorwaarden geeft: voor de oplossing S die voldoet aan (*) geldt S(0) = 0 en S'(0) =1 (S moet dus de sinus voorstellen) en voor de oplossing C van (*) geldt C(0)=1 en C'(0)=0 (C stelt dus de cosinus voor).

Stel vervolgens dat y(x) te schrijven is als machtreeks:

.

Door die machtreeks in (*) in te vullen vind je de coëfficienten van S(x) en van C(x) (dat zijn de gewone Taylorreeksen, die je nu dus vindt zonder te weten dat de afgeleide van S gelijk is aan C).

Vervolgens kan je bewijzen dat die reeksen uniform convergeren zodat je ze termsgewijs mag differentiëren. Dan vind je dat S'(x) = C(x).

Leuke opgave om eens in een nachtje uit te werken .

[ Bericht 0% gewijzigd door thenxero op 11-11-2012 22:20:18 ]

quote:

Op zondag 11 november 2012 21:21 schreef Amoeba het volgende:

[..]

Waar staat dat? Ik stel zelfs nog dat je heel leerzaam bent in mijn eigen quote. Ik krijg op m'n donder als ik die opgaven niet af heb. Kan ik er wat aan doen dat het boek fouten maakt..

Ik verkeerde in de veronderstelling dat je aan zelfstudie deed. Je kunt inderdaad niet voorkomen dat een auteur van een boek het niet zo nauw neemt, maar je kunt wel op zoek gaan naar betere boeken. Maar aangezien het geen zelfstudie is begrijp ik dat je toch geacht wordt je huidige boek te gebruiken.

quote:

Maar, hoe zou je dan bewijzen dat de [sin(x)]' = cos(x) met behulp van reeksen?

Een bewijs voor de differentieerbaarheid en de afgeleiden van sin x en cos x hangt af van de definitie die je hanteert voor de goniometrische functies. Als je uitgaat van de bekende meetkundige definitie aan de hand van de eenheidscirkel, dan kun je op verschillende manieren gebruik maken van goniometrische identiteiten om aan te tonen dat voor elke x ∈ R geldt:

(1) lim_h→0 (sin(x+h) - sin x)/h = cos x

Hierbij moet je dan gebruik maken van de 'standaardlimiet'

(2) lim_θ→0 sin θ / θ = 1

waarbij θ uiteraard in radialen is uitgedrukt. Deze limiet moet je natuurlijk ook eerst hebben aangetoond, waarvoor je gebruik maakt van een meetkundige beschouwing om te laten zien dat:

(3) cos θ < sin θ / θ < 1 (0 < |θ| < π/2)

waarna (2) volgt uit (3) met behulp van de insluitstelling én (en dat wordt vaak onder het vloerkleed geveegd) de continuïteit van de functie cos θ in het punt θ = 0. Die laatste moeilijkheid kan omzeild worden door eerst aan te tonen dat je hebt:

(4) 1 – θ² < sin θ / θ < 1 (0 < |θ| < π/2)

Een heel aanschouwlijk 'fysisch' getint bewijs voor de afgeleiden van de sinus en cosinus functies krijg je door de meetkundige definitie op te vatten als een parametervoorstelling van een puntdeeltje dat met een eenparige snelheid één in tegenwijzerzin langs de eenheidscirkel beweegt. De plaatsvector s(t) van de beweging als functie van de tijd t is dan:

(5) s(t) = cos t ∙ e_x + sin t ∙ e_y

En de eerste afgeleide van de plaatsvector s(t) naar de tijd is de snelheidsvector v(t), dus:

(6) v(t) = d(cos t)/dt ∙ e_x + d(sin t)/dt ∙ e_y

Maar we weten dat de snelheidsvector v(t) een lengte één heeft en tevens op ieder moment loodrecht op de plaatsvector s(t) staat omdat een raaklijn aan een cirkel loodrecht staat op de straal naar het raakpunt. Bovendien weten we dat de snelheidsvector v(t) steeds een kwart slag tegen de klok in is gedraaid ten opzichte van de plaatsvector s(t), omdat de beweging langs de eenheidscirkel in tegenwijzerzin verloopt. Dus hebben we ook:

(7) v(t) = cos(t +½π) ∙ e_x + sin(t +½π) ∙ e_y

En aangezien elke vector in R² op precies één manier kan worden uitgedrukt als een lineaire combinatie van e_x en e_y volgt uit (6) en (7) dus direct dat:

(8) d(cos t)/dt = cos(t + ½π) = -sin t

en:

(9) d(sin t)/dt = sin(t + ½π) = cos t

Als je sin x en cos x louter analytisch introduceert dan wordt het een ander verhaal maar hangt het bewijs voor de differentieerbaarheid en de afgeleiden van deze functies weer af van de manier waarop je ze hebt geïntroduceerd. Vaak wordt in de reële analyse eerst begonnen met een analytische definitie van bijvoorbeeld arctan x op R, omdat die is uit te drukken als een integraal met een algebraïsche integrand:

(10) arctan x = ∫₀^x dt/(1 + t²)

Dan kun je tan x definiëren op (-½π, ½π) als de inverse van arctan x en dan kun je sin x en cos x weer definiëren (en het domein uitbreiden naar R) aan de hand van tan x. Maar elegant is anders. In de complexe analyse worden cos z en sin z als analytische voortzetting van cos x en sin x meestal gedefinieerd op C met behulp van exp z, waarbij exp z dan (meestal) weer aan de hand van een machtreeks wordt gedefinieerd. Maar daar komt echt nog een aardig stukje wiskunde bij kijken om dat allemaal streng te verantwoorden. En de formule van Euler is dan een tautologie geworden en het bewijs dat d(cos z)/dz = -sin z en d(sin z)/dz = cos z triviaal.

[ Bericht 0% gewijzigd door Riparius op 12-11-2012 02:50:15 ]

quote:

Op zondag 11 november 2012 21:45 schreef Amoeba het volgende:
Net als opgave 9b.

druk sin(x) uit in e^ix en e^-ix
Waarbij je bij a aan moest toen dat:



Krijg je dit als uitwerking.

[ afbeelding ]

Het is de bedoeling dat je ziet dat op grond van:

(1) e^ix = cos x + i∙sin x

voor elke x ∈ R ook geldt:

(2) e^-ix = cos (-x) + i∙sin(-x)

En aangezien cos x een even functie is en sin x een oneven functie heb je dus:

(3) e^-ix = cos x - i∙sin x

Door optelling resp. aftrekking van de leden van (1) en (3) volgt dan onmiddellijk:

(4) cos x = (e^ix + e^-ix)/2

(5) sin x = (e^ix - e^-ix)/2i

Euler deed het trouwens in zijn Introductio precies andersom: hij leidde eerst (4) en (5) af en daaruit dan (1) en (3).

quote:

Vond ik mijn uitwerking met behulp van de integraalrekening (want de primitieve van cos(x) is sin(x)) toch een stuk eleganter. Ik vrees dat je toch wat 'leerzamer' bent.

Het is mij niet duidelijk wat je precies bedoelt, maar ik heb je boek hier niet, dus ik weet ook niet wat voor (al dan niet verborgen) vooronderstellingen er allemaal gemaakt worden. Als je mag gebruiken dat d(e^ix)/dx = i∙e^ix dan is de bepaling van de afgeleiden van cos x en sin x uit (4) resp. (5) natuurlijk triviaal, en dan zie ik niet in waarom je voor je opgave integraalrekening zou gebruiken.

[ Bericht 0% gewijzigd door Riparius op 12-11-2012 00:00:13 ]

(4) was gegeven. Dit moest je alleen nog even bewijzen dat dit klopte..

Nu moest je voor sin(x) ook zo'n uitdrukking verzinnen, ik heb enkel en alleen de primitieve genomen. Kom je op exact hetzelfde uit. Alhoewel ik er wel van uit ging dat afgeleide functies hetzelfde zijn in C..

oke ik voel me heel dom en het is ook maar een kleine vraag maar toch:

ik moet y weten van: 5=2x^0.5 + y^0.5 (je kan de machten als wortels zien, maar dat weten jullie ofc)

Ik haal y naar links, 5 naar rechts: y^0.5 = 5- 2x^0.5
dan beide termen ^2 -> y= (5 - 2x^0.5)^2
y= 25 - 4x

Maaar mijn vriend wolfram alpha zegt dat het y=4x-20x^0.5+25 moet zijn, ik geloof hem uiteraard, maar hoe kom ik aan die -20^0.5 ertussen??

BVD

quote:

Op zondag 11 november 2012 23:18 schreef Amoeba het volgende:
(4) was gegeven. Dit moest je alleen nog even bewijzen dat dit klopte..

Oh, op die manier.

quote:

Nu moest je voor sin(x) ook zo'n uitdrukking verzinnen, ik heb enkel en alleen de primitieve genomen. Kom je op exact hetzelfde uit. Alhoewel ik er wel van uit ging dat afgeleide functies hetzelfde zijn in C..

Inderdaad, verborgen aannames ...

Je had bijvoorbeeld ook kunnen gebruiken dat

sin x = cos(½π - x)