SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Ja, om te checken of het aan mij lag of dat er echt geen exacte uitdrukking voor is. Ik kwam uit op tan x = 1/(3+sqrt(3)). Hadden ze daar vroeger niet één of andere rekenlat voor?quote:Op maandag 8 oktober 2012 20:31 schreef Riparius het volgende:
[..]
Je zit toch niet stiekem een calculator of zo te gebruiken?


Achter in dat boekje staat toch hele tabel ofzo?quote:Op maandag 8 oktober 2012 20:33 schreef thenxero het volgende:
[..]
Ja, om te checken of het aan mij lag of dat er echt geen exacte uitdrukking voor is. Ik kwam uit op tan x = 1/(3+sqrt(3)). Hadden ze daar vroeger niet één of andere rekenlat voor?


Inderdaad, er waren goniometrische tafels en ik neem aan dat die ook op het examen gebruikt mochten worden of erbij werden geleverd. Maar niettemin is er een exact antwoord mogelijk bij het vraagstuk.quote:Op maandag 8 oktober 2012 20:46 schreef Fsmxi het volgende:
[..]
Achter in dat boekje staat toch hele tabel ofzo?


Deze vraag zou ook nu nog op het vwo gesteld kunnen worden, met een iets eenvoudigere goniometrische identiteit zoals eentje met 45 graden.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


Hieronder dan mijn uitwerking:
De driehoek is 2/3 keer zo groot als het vierkant met oppervlakte 1. Dat houdt in dat we een rechthoekige driehoek ABC hebben met een hypotenusa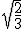
Goed, nu hebben we:
a2 + b2 = 2/3
a + b = 1
dus a = 1-b
substitutie levert op:
(1-b)2 + b2 = 2/3
1 + b2 -2b + b2 = 2/3
6b2 -6b + 1 = 0
De ABC formule:
[D = b2 -4ac]
D = 36 - 24 = 12
dus b =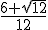
a =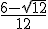
b = 1/2 + 1/6√3
a = 1/2 - 1/6√3
Nu is dus onze hoek x dus gelijk aan:
tan x = b/a = 6b/6a
tan x = (3+√3)/(3-√3)
Vermenigvuldigen met 3+3√3:
(9+6√3 +3) / ( 9 - 3)
= (12+6√3 )/ 6
= 2+√3
Nu geldt dat:
tan(2x) = 2tan(x) / (1 - tan2(x))
tan(x) = 2+√3
Vul in:
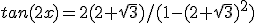
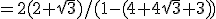
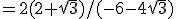
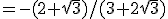
Vermenigvuldigen met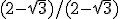
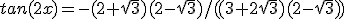
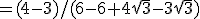
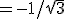
Aangezien 0 < x < 90° en dus 0 < 2x < 180° is dan 2x = 150° en dus x = 75°.
Met dank aan Riparius voor het laatste stukje.
QuiteEasilyDone
[ Bericht 9% gewijzigd door #ANONIEM op 09-10-2012 16:00:11 ]
De driehoek is 2/3 keer zo groot als het vierkant met oppervlakte 1. Dat houdt in dat we een rechthoekige driehoek ABC hebben met een hypotenusa
Goed, nu hebben we:
a2 + b2 = 2/3
a + b = 1
dus a = 1-b
substitutie levert op:
(1-b)2 + b2 = 2/3
1 + b2 -2b + b2 = 2/3
6b2 -6b + 1 = 0
De ABC formule:
[D = b2 -4ac]
D = 36 - 24 = 12
dus b =
a =
b = 1/2 + 1/6√3
a = 1/2 - 1/6√3
Nu is dus onze hoek x dus gelijk aan:
tan x = b/a = 6b/6a
tan x = (3+√3)/(3-√3)
Vermenigvuldigen met 3+3√3:
(9+6√3 +3) / ( 9 - 3)
= (12+6√3 )/ 6
= 2+√3
Nu geldt dat:
tan(2x) = 2tan(x) / (1 - tan2(x))
tan(x) = 2+√3
Vul in:
Vermenigvuldigen met
Aangezien 0 < x < 90° en dus 0 < 2x < 180° is dan 2x = 150° en dus x = 75°.
Met dank aan Riparius voor het laatste stukje.
QuiteEasilyDone
[ Bericht 9% gewijzigd door #ANONIEM op 09-10-2012 16:00:11 ]


Hoi, vandaag voor het eerst les in afgeleide functies gehad en ik ben nu hiermee aan het oefenen. Ik zoek de afgeleide van:
R2S + T
Moet de S in deze formule als constante behandeld worden?
Ik zelf denk zelf van wel en dat het dus: 2R moet zijn.
Want in principe staat er R2 x S + T als ik het goed heb.
R2S + T
Moet de S in deze formule als constante behandeld worden?
Ik zelf denk zelf van wel en dat het dus: 2R moet zijn.
Want in principe staat er R2 x S + T als ik het goed heb.


Correct. Maar dan is het niet 2R, maar 2SR.quote:Op maandag 8 oktober 2012 22:34 schreef BankzakenExpert het volgende:
Hoi, vandaag voor het eerst les in afgeleide functies gehad en ik ben nu hiermee aan het oefenen. Ik zoek de afgeleide van:
R2S + T
Moet de S in deze formule als constante behandeld worden?
Ik zelf denk zelf van wel en dat het dus: 2R moet zijn.
Want in principe staat er R2 x S + T als ik het goed heb.


Zonder verdere gegevens weet je niet of R,S, of T de variabele is (of dat er wellicht meerdere variabelen zijn). Als R de variabele is, dan is de afgeleide naar R gelijk aan 2RS. Als S de variabele is, dan R², en als T de variabele is dan is de afgeleide 1.quote:Op maandag 8 oktober 2012 22:34 schreef BankzakenExpert het volgende:
Hoi, vandaag voor het eerst les in afgeleide functies gehad en ik ben nu hiermee aan het oefenen. Ik zoek de afgeleide van:
R2S + T
Moet de S in deze formule als constante behandeld worden?
Ik zelf denk zelf van wel en dat het dus: 2R moet zijn.
Want in principe staat er R2 x S + T als ik het goed heb.


Tja, dat is erg flauw (of misschien sarcastisch bedoeld als indicatie van het huidige niveau) want als de hoek van de zijde van het ingeschreven vierkant met het grote vierkant 45 graden bedraagt dan is de oppervlakte van het ingeschreven vierkant precies de helft van het grote vierkant en omgekeerd. En dat wist Plato ook al.quote:Op maandag 8 oktober 2012 22:17 schreef GlowMouse het volgende:
Deze vraag zou ook nu nog op het vwo gesteld kunnen worden, met een iets eenvoudigere goniometrische identiteit zoals eentje met 45 graden.


Meestal staat er iets in de trant van:quote:Op maandag 8 oktober 2012 22:34 schreef BankzakenExpert het volgende:
Hoi, vandaag voor het eerst les in afgeleide functies gehad en ik ben nu hiermee aan het oefenen. Ik zoek de afgeleide van:
R2S + T
Moet de S in deze formule als constante behandeld worden?
Ik zelf denk zelf van wel en dat het dus: 2R moet zijn.
Want in principe staat er R2 x S + T als ik het goed heb.
Bereken de afgeleide van
Hier is expliciet vermeld dat f een functie van x is, dus is het gewoonlijk de bedoeling om naar x te differentiëren, dat wil zeggen: de andere variabelen als constant beschouwen. Soms gebruikt men ook wel de notatie:


Nou, wij hebben vandaag 3 methoden kort behandeld: Som, Quotiënt en product.
Y = (f)R = Pr2 + Qr / r2S + T
Hierbij is Quotiënt van toepassing.
Afgeleide 1e gedeelte = 2PR + Q
Afgeleide 2e gedeelte = 2R? of 2SR
Y = (f)R = Pr2 + Qr / r2S + T
Hierbij is Quotiënt van toepassing.
Afgeleide 1e gedeelte = 2PR + Q
Afgeleide 2e gedeelte = 2R? of 2SR


Heb je de reacties wel gelezen?quote:Op maandag 8 oktober 2012 23:05 schreef BankzakenExpert het volgende:
Nou, wij hebben vandaag 3 methoden kort behandeld: Som, Quotiënt en product.
Y = (f)R = Pr2 + Qr / r2S + T
Hierbij is Quotiënt van toepassing.
Afgeleide 1e gedeelte = 2PR + Q
Afgeleide 2e gedeelte = 2R? of 2SR


Wel de haakjes correct gebruiken. Je bedoelt:quote:Op maandag 8 oktober 2012 23:05 schreef BankzakenExpert het volgende:
Nou, wij hebben vandaag 3 methoden kort behandeld: Som, Quotiënt en product.
Y = (f)R = Pr2 + Qr / r2S + T
Hierbij is Quotiënt van toepassing.
Afgeleide 1e gedeelte = 2PR + Q
Afgeleide 2e gedeelte = 2R? of 2SR
Y = f(r) = Pr2 + Qr / r2S + T
Y is dus een functie van r en het is de bedoeling om de afgeleide van Y naar r te bepalen, dus dY/dr (notatie van Leibniz) oftewel f'(r) (notatie van Lagrange). Maar je moet hier beter niet met de quotiëntregel gaan werken. Gebruik de quotiëntregel alleen als het niet anders kan. En ja, het kán anders.


Oke, het is duidelijk.
De afgeleide van de noemer is 2RS.
Andere methoden als de quotiëntregel zullen we de volgende les wel krijgen dan.
De afgeleide van de noemer is 2RS.
Andere methoden als de quotiëntregel zullen we de volgende les wel krijgen dan.


Laat me je vertellen dat het niveau bedroevend is. Je denkt vast dat ik slechts een middelmatige leerling ben, maar van mijn school ben ik veruit de meest bedreven danwel gemotiveerde wiskundeleerling. Zelfs met een hoek van 45° zou 9/10 er nog niet uitkomen.quote:Op maandag 8 oktober 2012 22:58 schreef Riparius het volgende:
[..]
Tja, dat is erg flauw (of misschien sarcastisch bedoeld als indicatie van het huidige niveau) want als de hoek van de zijde van het ingeschreven vierkant met het grote vierkant 45 graden bedraagt dan is de oppervlakte van het ingeschreven vierkant precies de helft van het grote vierkant en omgekeerd. En dat wist Plato ook al.
Goed, ik moet wel bekennen dat ik een van de weinige vwo'ers ben tussen de havisten. Desalniettemin blijft het niveau treurig.
En om nog even terug te komen op de lesstof: De Moivre en een inleiding tot complexe getallen wordt behandeld in wiskunde D, vwo. Optioneel dus.
[ Bericht 5% gewijzigd door #ANONIEM op 09-10-2012 00:31:44 ]


Nou, ik betwijfel of je hetgeen je tot nu toe geleerd hebt dan wel begrepen hebt, of is het de bedoeling veel moeilijker te doen dan nodig?quote:Op maandag 8 oktober 2012 23:35 schreef BankzakenExpert het volgende:
Oke, het is duidelijk.
De afgeleide van de noemer is 2RS.
Andere methoden als de quotiëntregel zullen we de volgende les wel krijgen dan.
Ik neem aan dat je toch wel weet dat als:
f(r) = rn
dat dan geldt:
f'(r) = n∙rn-1
En je kent neem ik aan ook bepaalde rekenregels voor het werken met machten, bijvoorbeeld:
rm/rn = rm-n
Zo zou je kunnen zien dat je hebt:
f(r) = P∙r2 + (Q/S)∙r-1 + T
Probeer nu nog eens f'(r) te bepalen.


Riparius, ik vrees dat zijn formule er zo uitziet:
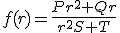
Of heb ik dit mis?
(Ondanks dat zijn haakjes anders impliceren, of beter gebrek aan)
[ Bericht 11% gewijzigd door #ANONIEM op 08-10-2012 23:48:07 ]
Of heb ik dit mis?
(Ondanks dat zijn haakjes anders impliceren, of beter gebrek aan)
[ Bericht 11% gewijzigd door #ANONIEM op 08-10-2012 23:48:07 ]


De uitwerking is correct, maar het is duidelijk dat een algebraïsche aanpak nogal wat rekenwerk oplevert.quote:Op maandag 8 oktober 2012 22:22 schreef Amoeba het volgende:
Hieronder dan mijn uitwerking:
[snip]
Met dank aan Riparius voor het laatste stukje.
De tangens 2 + √3 óf 2 - √3 van de gevraagde hoek is geen 'standaardwaarde', zodat de hoek moest worden opgezocht in een goniometrische tafel. Tegenwoordig gebruiken we daar uiteraard de arctan functie op de rekenmachine voor, en dan vinden we vlot dat arctan(2 + √3) = 75° resp. dat arctan(2 - √3) = 15°. De zijden van het grote vierkant worden door de hoekpunten van het ingeschreven vierkant elk in twee delen verdeeld, en de opgave heeft dan ook twee mogelijke uitkomsten, omdat niet geheel duidelijk is of de hoek van de zijde van het ingeschreven vierkant met het grootste of met het kleinste deel van de zijde van het grote vierkant wordt bedoeld. Maar deze hoeken zijn uiteraard complementair. Het bewijs dat de gevraagde hoek inderdaad exact 15° (= 45° - 30°) dan wel 75° (= 45° + 30°) bedraagt kan dan worden geleverd door aan de hand van de som of verschilformules voor de tangens en de 'standaardwaarden' tan 30° = (1/3)∙√3 en tan 45° = 1 te laten zien dat tan 15° = 2 - √3 resp. dat tan 75° = 2 + √3.
Eenvoudiger gaat het met een meetkundige beschouwing. De vier rechthoekige driehoeken die met het ingeschreven vierkant het grote vierkant vormen hebben samen een oppervlakte van 1/3 deel van het grote vierkant. Voegen we nu in de figuur nog vier hiermee congruente rechthoekige driehoeken toe zodanig dat de schuine zijden van de toegevoegde driehoeken elk tegen één van de schuine zijden van de reeds aanwezige rechthoekige driehoeken komen te liggen, dan beslaan de 8 rechthoekige driehoeken samen 2/3 deel van de oppervlakte van het grote vierkant en resteert in het centrum van het grote vierkant nog een klein vierkant waarvan de zijden evenwijdig zijn met die van het grote vierkant. De oppervlakte van dit kleine vierkant bedraagt dus 1/3 deel van die van het grote vierkant zodat de lengte van de zijde van dit kleine vierkant zich tot die van het grote vierkant verhoudt als √(1/3) : √1 = (1/3)∙√3 : 1.
Trekken we nu een diagonaal van het ingeschreven vierkant, dan hebben we in de figuur een rechthoekige driehoek waarvan deze diagonaal de hypotenusa vormt. De lengte van de diagonaal van het ingeschreven vierkant, en dus van de hypotenusa van deze rechthoekige driehoek, is (2/3)∙√3 maal de zijde van het grote vierkant, terwijl de rechthoekszijden van deze rechthoekige driehoek gelijk zijn aan de resp. de zijde van het grote vierkant en de zijde van het kleine centrale vierkant, oftewel 1 maal en (1/3)∙√3 maal de zijde van het grote vierkant. Deze rechthoekige driehoek vormt dus de helft van een gelijkzijdige driehoek, zodat de scherpe hoeken van deze rechthoekige driehoek 60° en 30° zijn. Maar dan volgt uit de figuur direct dat de zijde van het ingeschreven vierkant met het langste deel van de zijde van het grote vierkant een hoek vormt van 60° - 45° = 15° resp. dat de zijde van het ingeschreven vierkant met het kortste deel van de zijde van het grote vierkant een hoek vormt van 45° + 30° = 75°, QED.
[ Bericht 0% gewijzigd door Riparius op 09-10-2012 04:33:41 ]


Ah, op die manier. Maar goed, dan had hij inderdaad haakjes moeten gebruiken. En dan wordt het uiteraard wel een kwestie van de quotiëntregel gebruiken en krijgen we:quote:Op maandag 8 oktober 2012 23:47 schreef Amoeba het volgende:
Riparius, ik vrees dat zijn formule er zo uitziet:
Of heb ik dit mis?
(Ondanks dat zijn haakjes anders impliceren, of beter gebrek aan)
f'(r) = (-QSr2 + 2PTr + QT)/(Sr2 + T)2
[ Bericht 5% gewijzigd door Riparius op 09-10-2012 01:45:06 ]


Nog even een aanvulling. Ik bedacht dat het nog korter kan als je gebruik maakt van Pythagoras:quote:
De diagonalen AC en BD van het ingeschreven vierkant ABCD met een oppervlakte van 2/3 deel van de oppervlakte van het grote vierkant hebben een lengte van √2∙√(2/3) = (2/3)∙√3 maal de lengte van de zijde van het grote vierkant. Laten we nu vanuit punt A een loodlijn neer op de tegenoverliggende zijde van het grote vierkant en is P het voetpunt van deze loodlijn, dan heeft lijnstuk PC volgens Pythagoras een lengte van (1/3)∙√3 maal de lengte van de zijde van het grote vierkant, zodat PC = ½∙AC. De rechthoekige driehoek ACP is dus de helft van een gelijkzijdige driehoek, zodat ∠ACP = 60°. Nu is ook ∠ACD = 45° en dus is ∠DCP = ∠ACP - ∠ACD = 60° - 45° = 15°, QED.
[ Bericht 10% gewijzigd door Riparius op 09-10-2012 21:50:27 ]


Ik heb een vraag over lineaire afhankelijkheid van vectoren ( lineaire algebra).
In mijn boek staat dat als je een matrix A en een vector x hebt en Ax=0, en je rij-reduceert deze matrix naar een matrix H zodat Hx=0, als de i'de kolom van H dan geen zogenaamde ''pivot'' heeft, dan is de i'de kolomvector van A lineair afhankelijk. Waarom is dit? Ik snap niet hoe je dat kunt zeggen over de kolomvectoren van A terwijl je kijkt naar H. Als je elementaire rij operaties uitvoert op A om H te krijgen, danverander je toch de kolomvectoren steeds?(bij elke rijoperatie verander je toch dezelfde component (bijvoorbeeld de x-component van alle vectoren) van alle kolomvectoren?)
danku
In mijn boek staat dat als je een matrix A en een vector x hebt en Ax=0, en je rij-reduceert deze matrix naar een matrix H zodat Hx=0, als de i'de kolom van H dan geen zogenaamde ''pivot'' heeft, dan is de i'de kolomvector van A lineair afhankelijk. Waarom is dit? Ik snap niet hoe je dat kunt zeggen over de kolomvectoren van A terwijl je kijkt naar H. Als je elementaire rij operaties uitvoert op A om H te krijgen, danverander je toch de kolomvectoren steeds?(bij elke rijoperatie verander je toch dezelfde component (bijvoorbeeld de x-component van alle vectoren) van alle kolomvectoren?)
danku


Je vergeet te noemen dat x geen 0 mag zijn en dat H in echelonvorm moet staan.quote:Op dinsdag 9 oktober 2012 20:27 schreef flopsies het volgende:
Ik heb een vraag over lineaire afhankelijkheid van vectoren ( lineaire algebra).
In mijn boek staat dat als je een matrix A en een vector x hebt en Ax=0, en je rij-reduceert deze matrix naar een matrix H zodat Hx=0, als de i'de kolom van H dan geen zogenaamde ''pivot'' heeft, dan is de i'de kolomvector van A lineair afhankelijk. Waarom is dit? Ik snap niet hoe je dat kunt zeggen over de kolomvectoren van A terwijl je kijkt naar H. Als je elementaire rij operaties uitvoert op A om H te krijgen, danverander je toch de kolomvectoren steeds?(bij elke rijoperatie verander je toch dezelfde component (bijvoorbeeld de x-component van alle vectoren) van alle kolomvectoren?)
Door ero's veranderen de kolomvectoren inderdaad, maar lineaire afhankelijkheden tussen de kolommen veranderen niet. Dat zie je zelf ook al omdat je dezelfde x gebruikt.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0


