SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
En zoals je kunt zien is het dus foutgevoelig want even checken in wolfram alpha levert iets heuul anders op.
EDIT: inmiddels is de fout gevonden en alweer gecorrigeerd. Je kan hem nu zonder meer overnemen
[ Bericht 24% gewijzigd door VanishedEntity op 16-08-2012 21:57:03 ]
EDIT: inmiddels is de fout gevonden en alweer gecorrigeerd. Je kan hem nu zonder meer overnemen
[ Bericht 24% gewijzigd door VanishedEntity op 16-08-2012 21:57:03 ]
Dat is een hele riedel! Bedankt, ik zal er nog even rustig naar kijken, maar ik denk niet dat ik zo'n bewerkelijke integraal moet kunnen oplossen. Kennelijk gingen zij daar ook niet vanuit in de vraag. Ik heb nog even een simpele vraag:
f(x) = cos 2x/x-3? Daarmee kom ik niet op het juiste antwoord.
Bij voorbaat dank.
[ Bericht 0% gewijzigd door Warren op 16-08-2012 22:45:17 ]
Nu wordt voorgesteld om dat te doen via f(x) = x3 / sec 2x, maar dit kan toch ook viaquote:Verify the solution to problem 12.39 (3x2 cos 2x - 2x3 sin 2x) by differentiating f(x) = x3 cos 2x. using the quotient rule
f(x) = cos 2x/x-3? Daarmee kom ik niet op het juiste antwoord.
Bij voorbaat dank.
[ Bericht 0% gewijzigd door Warren op 16-08-2012 22:45:17 ]
Als ik dat zo bekijk zie ik helemaal geen breuken staan dus is het "domweg" een kwestie van de productregel hanteren:
(x3*cos2x)' = (x3)' *cos2x + x3*(cos2x)' =
3x2*cos2x - x3*2*sin2x =
3x2*cos2x - 2x3*sin2x
Maargoed, ze willen het dus op de dom-ingewikkelde manier;
( x3/sec(2x) )' =
(x3)' *sec2x - (sec2x)' *x3
----------------------------------
sec22x
=
3x2*sec2x - x3*(+2sin2x/cos22x)
---------------------------------------------------
sec22x
=
3x2/cos2x - x3*(2sin2x/cos22x)
---------------------------------------------------
sec22x
=
3x2*cos2x/cos22x - x3*(2sin2x/cos22x)
---------------------------------------------------
sec22x
=
3x2*cos2x - x3*(2sin2x)
---------------------------------------------------
sec22x * cos22x
=
3x2*cos2x - x3*(2sin2x)
---------------------------------------------------
1
=
3x2*cos2x - x3*(2sin2x)
klaar
[ Bericht 8% gewijzigd door VanishedEntity op 16-08-2012 23:22:48 ]
(x3*cos2x)' = (x3)' *cos2x + x3*(cos2x)' =
3x2*cos2x - x3*2*sin2x =
3x2*cos2x - 2x3*sin2x
Maargoed, ze willen het dus op de dom-ingewikkelde manier;
( x3/sec(2x) )' =
(x3)' *sec2x - (sec2x)' *x3
----------------------------------
sec22x
=
3x2*sec2x - x3*(+2sin2x/cos22x)
---------------------------------------------------
sec22x
=
3x2/cos2x - x3*(2sin2x/cos22x)
---------------------------------------------------
sec22x
=
3x2*cos2x/cos22x - x3*(2sin2x/cos22x)
---------------------------------------------------
sec22x
=
3x2*cos2x - x3*(2sin2x)
---------------------------------------------------
sec22x * cos22x
=
3x2*cos2x - x3*(2sin2x)
---------------------------------------------------
1
=
3x2*cos2x - x3*(2sin2x)
klaar
[ Bericht 8% gewijzigd door VanishedEntity op 16-08-2012 23:22:48 ]
Een tip: met de produktregel kan je soms jezelf werk besparen doordat de algebraïsche uitwerking simpeler is.
De afgeleide (3x-5)*(8x+6) kan je bijvoorbeeld ook met de produktregel berekenen, dat is dan 3(8x+6)+8(x-5). In dit geval maakt het weinig uit maar als er hogere exponenten en meer termen binnen die haakjes staan dan kan je het jezelf heel wat gemakkelijker maken.
De afgeleide (3x-5)*(8x+6) kan je bijvoorbeeld ook met de produktregel berekenen, dat is dan 3(8x+6)+8(x-5). In dit geval maakt het weinig uit maar als er hogere exponenten en meer termen binnen die haakjes staan dan kan je het jezelf heel wat gemakkelijker maken.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Bovenstaande voorbeeld lijkt me wel duidelijk genoeg aangeven dat de productregel als het ff kan te prefereren valt boven de quotiëntregel.
Bedankt. De breuk waar het om ging wasquote:Op donderdag 16 augustus 2012 23:05 schreef VanishedEntity het volgende:
Als ik dat zo bekijk zie ik helemaal geen breuken staan dus is het "domweg" een kwestie van de productregel hanteren:
Maar het is nu gelukt via:
Jouw methode stond in de uitwerking, maar het ging mij om de bovenstaande. Maar dat is nu gelukt, ik maakte eerst steeds dezelfde fout met de exponenten.
De quotiëntregel is een afgeleide van de produktregel, je kan die afleiding zelf vrij gemakkelijk maken. Wat te prefereren valt hangt af van de complexiteit van hetgeen je moet afleiden.quote:Bovenstaande voorbeeld lijkt me wel duidelijk genoeg aangeven dat de productregel als het ff kan te prefereren valt boven de quotiëntregel.
6/x^3 kan je gemakkelijker met de produktregel afleiden door in te zien dat dat hetzelfde is als 6x^-3 , 5x^3 + 9x -5(sinh (²log(14)) / 8x^4 - 5cos(pi) + ln(arctan(5x) differentieer ik toch liever met de quotiëntregel.
[ Bericht 0% gewijzigd door Bram_van_Loon op 17-08-2012 16:30:15 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
In Nederland wordt niet (meer) van je verwacht dat je deze kunt oplossen, maar in Vlaams studiemateriaal voor het middelbaar ben ik hem wel eens tegengekomen.quote:
[..]
Ok, maar ik ging er vanuit dat dit bekend werd verondersteld. BTW, dit is van het toelatingsexamen arts. Zou dit kunnen betekeken dat je zulke "lastige" integralen niet hoeft te kunnen doen?
De bedoeling van deze opgave is alleen dat je er blijk van geeft te begrijpen dat (en waarom) <A> <B> en <C> niet juist kunnen zijn.
Deze integraal is onlangs nog voorbij gekomen in deze topicreeks en is een klassieker omdat deze een rol speelt bij de Mercator kaartprojectie. Er zijn verschillende mogelijkheden om 1/cos x te primitiveren. Als je eens een paar van die mogelijkheden wil zien (en antwoord wil hebben op je vraag) kan ik je aanraden dit en dit en dit eens door te nemen.quote:Waarom mag je deze integraal overigens niet naar analogie van 1/x oplossen, zoals ik dat dus dacht?
Ik heb daar nog een leuk werkstuk over gemaakt. Nu we het er toch weer over hebben, ik wil mijn profielwerkstuk centreren rondom het onderwerp cartografie. Een deelonderwerp heb ik dus al, de Mercatorprojectie. De bedoeling is echt wiskunde, geen geschiedenis. Wat voor interessants zou ik nog meer kunnen bijvoegen?
Fervent tegenstander van het korps lasergamers.
@Riparius. Bedankt, ik zal er naar kijken.
Ik heb nog een vraag. De afgeleide van
is 1/x, maar klopt het dat de afgeleide van ln 2x+2 gelijk is aan:
?
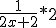Ik heb nog een vraag. De afgeleide van
Je hebt correct de kettingregel toegepast.quote:
@Riparius. Bedankt, ik zal er naar kijken.
Ik heb nog een vraag. De afgeleide van
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Bedankt BvL en GM. Ik zag eerst niet dat de vergelijkingen van logaritmische en exponentiële vergelijkingen ook gebruik maken van de kettingregel.
ln(2x+1) bestaat uit ln(x) en (2x+1).
ln(2x+1) bestaat uit ln(x) en (2x+1).
Dat zie je dan weer wel fout. Je neemt het natuurlijk logaritme van een x-waarde waar een vermenigvuldiging t.o.v. de y-as met 1/2 wordt toegepast en vervolgens een translatie van (-1, 0).quote:
Bedankt BvL en GM. Ik zag eerst niet dat de vergelijkingen van logaritmische en exponentiële vergelijkingen ook gebruik maken van de kettingregel.
ln(2x+1) bestaat uit ln(x) en (2x+1).
Ik denk dat je bedoelt:
ln(2x+1) bestaat uit ln(u) met u = 2x+1.
Fervent tegenstander van het korps lasergamers.
Maar wat als ik heb:quote:
[..]
Dat zie je dan weer wel fout. Je neemt het natuurlijk logaritme van een x-waarde waar een vermenigvuldiging t.o.v. de y-as met 1/2 wordt toegepast en vervolgens een translatie van (-1, 0).
Ik denk dat je bedoelt:
ln(2x+1) bestaat uit ln(u) met u = 2x+1.
y = (x2 + 1)5.
Mag ik dan wel zeggen dat deze bestaat uit f(x) = x5 en g(x) = x2+1?
Lees in Wikipedia eens de artikelen over samengestelde functies en de kettingregel, alsmede de substitutieregel bij de integraalrekening die je als de tegenhanger van de kettingregel bij de differentiaalrekening kunt beschouwen.quote:
[..]
Maar wat als ik heb:
y = (x2 + 1)5.
Mag ik dan wel zeggen dat deze bestaat uit f(x) = x5 en g(x) = x2+1?
Kan, en dan in dat geval zou ik vervolgens definiëren h(x) = f(g(x)) = (x2+1)5.quote:
[..]
Maar wat als ik heb:
y = (x2 + 1)5.
Mag ik dan wel zeggen dat deze bestaat uit f(x) = x5 en g(x) = x2+1?
Maar meestal hebben ze f(x) al gedefinieerd als de volledige functie; dan zou ik hem opsplitsen als g(x) = x5 en h(x) = x2+1
Je hebt gelijk hoor, alleen je formuleert het een beetje vaag waardoor Amoeba erover struikelt. Je bedoelt f(x)=2x+1 en g(x)=ln(x). Dan geldt ln(2x+1) = g(f(x)), en dus heb je een kettingfunctie.quote:
Bedankt BvL en GM. Ik zag eerst niet dat de vergelijkingen van logaritmische en exponentiële vergelijkingen ook gebruik maken van de kettingregel.
ln(2x+1) bestaat uit ln(x) en (2x+1).
Je snapt het goed.quote:
[..]
Kan, en dan in dat geval zou ik vervolgens definiëren h(x) = f(g(x)) = (x2+1)5.
Maar meestal hebben ze f(x) al gedefinieerd als de volledige functie; dan zou ik hem opsplitsen als g(x) = x5 en h(x) = x2+1
Dan heb je de kettingregel nog niet voldoende begrepen. Dat is heel erg normaal hoor, niets om je zorgen over te maken, maar het is wel goed om je daar bewust van te zijn.quote:Ik zag eerst niet dat de vergelijkingen van logaritmische en exponentiële vergelijkingen ook gebruik maken van de kettingregel.
Laat ik eens een paar voorbeeldjes geven van het gebruik van de kettingregel. Wanneer je een functie arctan(x) hebt dan is de afgeleide (1)/(1+x²). Stel dat er nu in plaats van arctan(x) arctan(5*x²) staat dan is de afgeleide 10*x / (1 + (5*x²)²) = 10x / (1 + 25x^4)
Stel dat er arctan(ln(cos(x)) staat dan is de afgeleide = [-sin(x) / (cos(x)] / [1 + (ln(cos(x)))²].
Stel dat er arctan(sin(ln(16x²))) staat dan is de afgeleide [cos(ln(16x²)) * 32x / 16x²] / [1 + (sin(ln(16x²)))²]
Hopelijk staan er geen fouten in, anders wordt het snel genoeg opgemerkt.
PS
Ik had op dit tijdstip even geen zin om de LaTeX-code op te zoeken, tijd om van het goede voornemen om meer met LaTeX te werken eens werk te maken.
De laatste twee vergelijkingen kunnen wat eleganter worden uitgewerkt maar dat is hier het punt niet.
[ Bericht 2% gewijzigd door Bram_van_Loon op 19-08-2012 16:27:24 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Bedankt, dat is ook hoe het in The Complete Idiot's Guide to Calculus staat uitgelegd en zo had ik het moeten opschrijven.quote:
Je hebt gelijk hoor, alleen je formuleert het een beetje vaag waardoor Amoeba erover struikelt. Je bedoelt f(x)=2x+1 en g(x)=ln(x). Dan geldt ln(2x+1) = g(f(x)), en dus heb je een kettingfunctie.
@ BvL. Ik snap jouw uitleg. Arctan (5x2) is een samengestelde functie.
Ik heb nog een andere vraag. Als ik moet beoordelen of y = (x2)/(3x+2) twee of geen buigpunten heeft (zonder GR), dan neem ik aan dat het niet de bedoeling is om een tweede afgeleide te nemen en deze gelijk te stellen met 0? De tweede afgeleide wordt namelijk een flinke riedel. Klopt het dat je moet inzien dat het een of andere kegelsnede functie is? Ik heb namelijk alleen maar cirkels en parabolen gehad (deze twee zijn alleen maar vereist voor het toelatingsexamen), maar deze zijn het niet volgens mij. Kegelsnede functies hebben namelijk geen buigpunten.
De grafiek hiervan is een hyperbool en die heeft inderdaad geen buigpunten. Kegelsneden zijn tweedegraads krommen.quote:
[..]
Ik heb nog een andere vraag. Als ik moet beoordelen of y = (x2)/(3x+2) twee of geen buigpunten heeft (zonder GR), dan neem ik aan dat het niet de bedoeling is om een tweede afgeleide te nemen en deze gelijk te stellen met 0? De tweede afgeleide wordt namelijk een flinke riedel. Klopt het dat je moet inzien dat het een of andere kegelsnede functie is? Ik heb namelijk alleen maar cirkels en parabolen gehad (deze twee zijn alleen maar vereist voor het toelatingsexamen), maar deze zijn het niet volgens mij. Kegelsnede functies hebben namelijk geen buigpunten.
Bedankt. Als regel kan ik aanhouden dat tweedegraadskrommes nooit een buigpunt hebben? Want y = (x2)/(3x+2) heeft ook geen buigpunten. Lijkt me ook logisch op zich, want f(x) = x2 heeft wel een eerste afgeleide, f'(x) = 2x, maar de derde afgeleide zou dan luiden f''(x) = 2 en deze derde afgeleide is niet gelijk te stellen met 0.quote:
[..]
De grafiek hiervan is een hyperbool en die heeft inderdaad geen buigpunten. Kegelsneden zijn tweedegraads krommen.
f(x) = x3 heeft wel een buigpunt als ik het goed heb, op x = 0.
Sorry voor deze "domme" vragen, ik heb nooit wiskunde B gehad op school.
Inderdaad. Tweedegraads krommen zijn kegelsneden en die hebben geen buigpunten.quote:
[..]
Bedankt. Als regel kan ik aanhouden dat tweedegraadskrommen nooit een buigpunt hebben?
Dat is in beginsel juist, maar een tweedegraads kromme hoeft niet de grafiek te zijn van een tweedegraads functie. De eenheidscirkel heeft bijvoorbeeld als vergelijkingquote:Want y = (x2)/(3x+2) heeft ook geen buigpunten. Lijkt me ook logisch op zich, want f(x) = x2 heeft wel een eerste afgeleide, f'(x) = 2x, maar de derde afgeleide zou dan luiden f''(x) = 2 en deze derde afgeleide is niet gelijk te stellen met 0.
x2 + y2 = 1,
maar de eenheidscirkel is niet de grafiek van een tweedegraads functie. Een tweedegraads functie is in het algemeen van de gedaante f(x) = ax2 + bx + c (met a ongelijk aan nul), en de grafiek daarvan is altijd een parabool.
Dat is juist. Je kunt natuurlijk altijd WolframAlpha even een grafiekje laten tekenen.quote:f(x) = x3 heeft wel een buigpunt als ik het goed heb, op x = 0.
quote:Sorry voor deze "domme" vragen, ik heb nooit wiskunde B gehad op school.
Ik vind het altijd nuttig om te beginnen met die functie wat te onderzoeken. Vul een aantal kleine getallen in, positief en negatief, vul wat grote getallen in en bedenk dat de noemer nul kan worden. Sowieso zie je direct dat je x/3 als limiet krijgt voor hele grote getallen en -x/3 voor hele kleine getallen aangezien die +2 in de noemer verwaarloosbaar is bij absoluut grote getallen.quote:Ik heb nog een andere vraag. Als ik moet beoordelen of y = (x2)/(3x+2) twee of geen buigpunten heeft (zonder GR), dan neem ik aan dat het niet de bedoeling is om een tweede afgeleide te nemen en deze gelijk te stellen met 0?
Je zou ook direct moeten zien dat je bij kleine getallen voor x<-2/3 het negatieve krijgt van wat je voor x>-2/3 krijgt en dat de grafiek niet loopt op x=-2/3. Als je dat alles zelf bedenkt dan trek je direct de conclusie dat de grafiek een hyperbool is.
In het verleden werden leerlingen gedwongen om uit zichzelf eerst en vooral eens de functie kritisch te bekijken, tegenwoordig kunnen de meeste leerlingen dat niet doordat ze gewend zijn om het GR het werk te laten doen. Doe zoveel mogelijk werk zelf, leun zo weinig mogelijk op het GR. Dat geldt bijvoorbeeld ook voor de meeste algebra. Bij een vergelijking als 5*sinx = 2cos(x) of x³+5x²=6x moet je echt niet het GR gebruiken, je moet dat even met de hand uitwerken. Altijd eerst zelf proberen!
Helaas geven ze op het VWO (inclusief examen!) vergelijkingen die niet met de hand op te lossen zijn en op het examen kan je ook rustig het GR gebruiken (je moet wel, de hoeveelheid vragen is eraan aangepast) maar probeer dat tijdens het oefenen te vermijden.
Hoe ga jij examen doen voor wiskunde? Je kan dat ook via de OU doen als de universiteit dat aanvaardt. Ik heb ze slechts oppervlakkig ingekeken maar ik had sterk de indruk dat die examens kwalitatief beter zijn dan de centrale examens.
[ Bericht 5% gewijzigd door Bram_van_Loon op 19-08-2012 16:49:00 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
@Riparius. Bedankt voor jouw uitleg 
Ik ga geen examen doen voor wiskunde. Ik ben aan het oefenen voor het toelatingsexamen arts/tandarts in België.quote:
Hoe ga jij examen doen voor wiskunde? Je kan dat ook via de OU doen als de universiteit dat aanvaardt. Ik heb ze slechts oppervlakkig ingekeken maar ik had sterk de indruk dat die examens kwalitatief beter zijn dan de centrale examens.
