SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Je antwoord voor de concentratie van oplossing I is goed.quote:Op woensdag 13 juni 2012 12:44 schreef daantje1044 het volgende:
Ik heb weer eens een vraag.
De opgave is: 17.34 g Kaliumhydroxide wordt opgelost in een maatkolf van 200 ml (oplossing I). oplossing II wordt verkregen door 10.00 ml van oplossing I met water aan te vullen tot 150.0 ml. Tot slot wordt 25.00 ml van oplossing II tot neutraal getitreerd met een 0.138 M HCL-oplossing in water.
De eerste vraag was: Wat is de KOH-concentratie in mol/l in oplossing I?
Die heb ik als volgt uitgerekend:
n= m/M dus n= 17,34 g/ (39.10 + 16.00 + 1.0079) = 0.309 mol
c= n/V dus c= 0.309 mol/ 0.200L = 1.55 mol/L
De volgende vraag kom ik niet uit
Wat is de KOH concentratie in oplossing II?
Zou iemand me daarmee op weg kunnen helpen?
Alvast bedankt.
Om de concentratie van oplossing II te bepalen kun je 2 methoden gebruiken.
1) De simpelste methode is berekenen hoeveel keer er wordt verdund om oplossing II te verkrijgen. Delen van de concentratie van I door de verdunningsgraad geeft het antwoord.
2) Een wat omslachtigere wijze is eerst berekenen hoeveel mol KOH er aanwezig is in 10 ml oplossing van I en dan berekenen wat de concentratie is als dat aantal mol wordt opgelost in 150 ml.
SPOILER: oplossing volgens methode 1Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.SPOILER: oplossing volgens methode 2Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Bedankt weer! zat al te denken aan oplossing 1, maar dacht dat dat te makkelijk gedacht was van me. Niet zo moeilijk denken dus.
Heb nog een vraag.
Gegeven: oplossing I: 100ml, 0.5 M Pb(NO3)2 (aq) en oplossing II: 75 ml 0.4 M K2SO4.
nu is de vraag hoeveel gram neerslag kan er maximaal ontstaan?
Ik heb al uitgerekend dat oplossing I 100 ml * 0.5 M = 50 mmol Pb(NO3)2 bevat.
Oplossing II bevat 75ml * 0.4 M = 30 mmol K2SO4.
de netto reactie is:
Pb2+ + SO42- ---> PbSO4
de beperkende reactant is SO42-.
Als ik nu 30 mmol * de molaire massa van PbSO4 doe, bereken ik dan hoeveel gram neerslag er kan ontstaan? Ik dacht dat het zo moest, maar kom daarmee niet op het goede antwoord uit.
Heb nog een vraag.
Gegeven: oplossing I: 100ml, 0.5 M Pb(NO3)2 (aq) en oplossing II: 75 ml 0.4 M K2SO4.
nu is de vraag hoeveel gram neerslag kan er maximaal ontstaan?
Ik heb al uitgerekend dat oplossing I 100 ml * 0.5 M = 50 mmol Pb(NO3)2 bevat.
Oplossing II bevat 75ml * 0.4 M = 30 mmol K2SO4.
de netto reactie is:
Pb2+ + SO42- ---> PbSO4
de beperkende reactant is SO42-.
Als ik nu 30 mmol * de molaire massa van PbSO4 doe, bereken ik dan hoeveel gram neerslag er kan ontstaan? Ik dacht dat het zo moest, maar kom daarmee niet op het goede antwoord uit.
In principe zou je hiermee op het juiste antwoord moeten komen, maar ik zou het iets anders opschrijven.quote:
Bedankt weer! zat al te denken aan oplossing 1, maar dacht dat dat te makkelijk gedacht was van me. Niet zo moeilijk denken dus.
Heb nog een vraag.
Gegeven: oplossing I: 100ml, 0.5 M Pb(NO3)2 (aq) en oplossing II: 75 ml 0.4 M K2SO4.
nu is de vraag hoeveel gram neerslag kan er maximaal ontstaan?
Ik heb al uitgerekend dat oplossing I 100 ml * 0.5 M = 50 mmol Pb(NO3)2 bevat.
Oplossing II bevat 75ml * 0.4 M = 30 mmol K2SO4.
de netto reactie is:
Pb2+ + SO42- ---> PbSO4
de beperkende reactant is SO42-.
Als ik nu 30 mmol * de molaire massa van PbSO4 doe, bereken ik dan hoeveel gram neerslag er kan ontstaan? Ik dacht dat het zo moest, maar kom daarmee niet op het goede antwoord uit.
Je berekening dat er 50 mmol Pb(NO3)2 is opgelost klopt, maar je moet er nog wel bijschrijven dat 50 mmol Pb(NO3)2 ook 50 mmol Pb2+ bevat. Idem voor kaliumsulfaat: 30 mmol opgelost K2SO4 bevat 30 mmol SO42-.
Omdat het lood- en sulfaation reageren in de verhouding die jij ook opschrijft (1 mol lood reageert met 1 mol sulfaat en geeft 1 mol loodsulfaat), kan er niet meer loodsulfaat ontstaan dan er van de beperkende reactant aanwezig is: inderdaad 50 mmol lood, en slechts 30 mmol sulfaat, dus maximaal 30 mmol loodsulfaat.
30 mmol * de molmassa van loodsulfaat zou het antwoord moeten geven: 0,030* 303,3 = 9,1 g PbSO4
Ok dank je wel, zal het duidelijker uitschrijven dan, zou zonde zijn als ik daar dan punten op laat liggen, maar dan had ik het toch goed gedaan, op mijn antwoordblad kwamen ze op 11,2 g PbSO4 uit.quote:Op woensdag 13 juni 2012 14:15 schreef lyolyrc het volgende:
[..]
In principe zou je hiermee op het juiste antwoord moeten komen, maar ik zou het iets anders opschrijven.
Je berekening dat er 50 mmol Pb(NO3)2 is opgelost klopt, maar je moet er nog wel bijschrijven dat 50 mmol Pb(NO3)2 ook 50 mmol Pb2+ bevat. Idem voor kaliumsulfaat: 30 mmol opgelost K2SO4 bevat 30 mmol SO42-.
Omdat het lood- en sulfaation reageren in de verhouding die jij ook opschrijft (1 mol lood reageert met 1 mol sulfaat en geeft 1 mol loodsulfaat), kan er niet meer loodsulfaat ontstaan dan er van de beperkende reactant aanwezig is: inderdaad 50 mmol lood, en slechts 30 mmol sulfaat, dus maximaal 30 mmol loodsulfaat.
30 mmol * de molmassa van loodsulfaat zou het antwoord moeten geven: 0,030* 303,3 = 9,1 g PbSO4
Vandaar dat ik ook niet snapte wat ik nu fout deed. Ik kwam zelf namelijk ook op 9,1 g uit.
Bedankt!
Bij de meeste toetsen wordt ook gekeken naar hoe je tot het antwoord komt, vandaar dat zorgvuldig uitwerken van belang is. En het zou inderdaad zonde zijn als je dan punten daarop laat liggen, terwijl je wel snapt hoe je tot het juiste antwoord moet komen.quote:
[..]
Ok dank je wel, zal het duidelijker uitschrijven dan, zou zonde zijn als ik daar dan punten op laat liggen, maar dan had ik het toch goed gedaan, op mijn antwoordblad kwamen ze op 11,2 g PbSO4 uit.
Vandaar dat ik ook niet snapte wat ik nu fout deed. Ik kwam zelf namelijk ook op 9,1 g uit.
Bedankt!
Antwoordbladen bevatten wel vaker fouten. Ik denk wel eens dat ze expres fouten erin zetten om studenten nog wat extra te laten zweten.
Denk het ook ja, ik maar denken wat doe ik toch fout? drie keer die molaire massa nagerekend, maar bleef maar op 9,1 uit komen hahaha.quote:
[..]
Bij de meeste toetsen wordt ook gekeken naar hoe je tot het antwoord komt, vandaar dat zorgvuldig uitwerken van belang is. En het zou inderdaad zonde zijn als je dan punten daarop laat liggen, terwijl je wel snapt hoe je tot het juiste antwoord moet komen.
Antwoordbladen bevatten wel vaker fouten. Ik denk wel eens dat ze expres fouten erin zetten om studenten nog wat extra te laten zweten.
. blij dat ik het toch even nagevraagd heb.
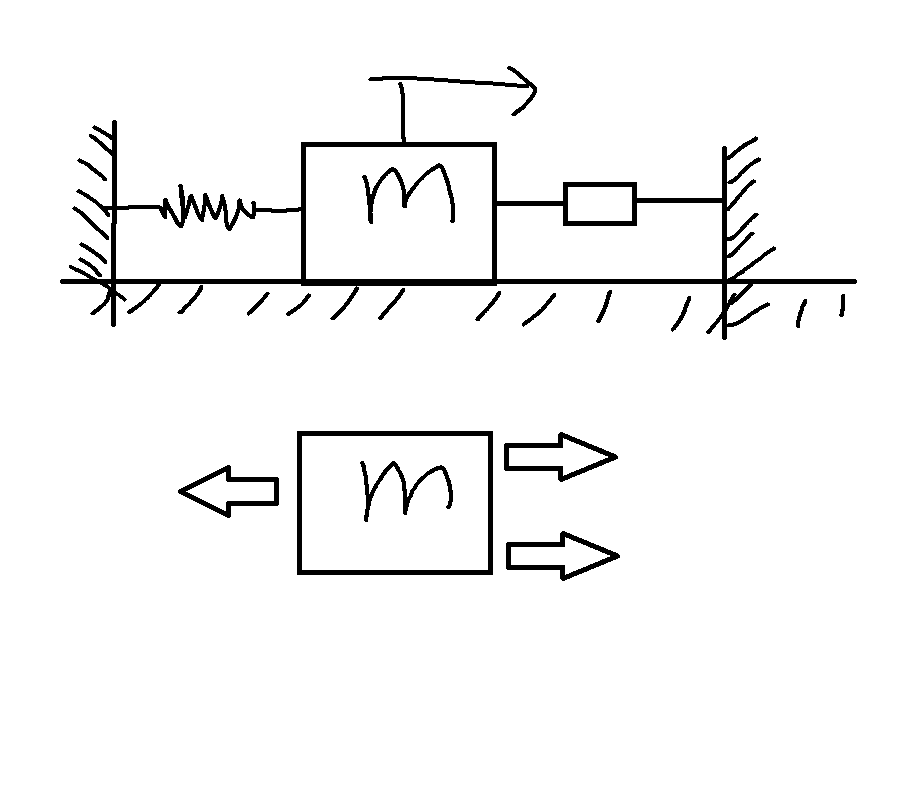
Ik heb weer iets heel simpels waar ik weer over na ga denken totdat ik mezelf niet meer snap:
Hier een simpel veer demper systeem. Als je daar een VLS van tekent hoe komen de krachten dan?
Die van de veer wijst naar links dat weet ik zeker maar van de demper gaat die ook naar links of toch naar rechts. Pijl boven op het blok is gewoon een externe kracht bijv.
Hier een simpel veer demper systeem. Als je daar een VLS van tekent hoe komen de krachten dan?
Die van de veer wijst naar links dat weet ik zeker maar van de demper gaat die ook naar links of toch naar rechts. Pijl boven op het blok is gewoon een externe kracht bijv.
Blues ain't nothing but a good man feeling bad...
Dat is zeker iets waarover je niet moet gaan nadenken tot je hoofdpijn hebt.quote:
Ik heb weer iets heel simpels waar ik weer over na ga denken totdat ik mezelf niet meer snap:
[ afbeelding ]
Hier een simpel veer demper systeem. Als je daar een VLS van tekent hoe komen de krachten dan?
Die van de veer wijst naar links dat weet ik zeker maar van de demper gaat die ook naar links of toch naar rechts. Pijl boven op het blok is gewoon een externe kracht bijv.
Het antwoord is heel simpel: kies wat je handig lijkt, maar teken wel de reactiekrachten juist (lees: tegengesteld) in.
Nog maar even een paint en uitleg om duidelijk te maken waarom het niets uitmaakt:
Als we x naar rechts als positief kiezen, dan geldt voor A:
-Fs + Fd = mx" (1)
Fs = k(x-0) = kx (2)
Fd = d(0-x') = -dx' (3)
Substitueren van de (2) en (3) in (1) geeft
-kx - dx' = mx"
We kiezen wederom x naar rechts als positief en dan vinden we voor B:
Fs - Fd = mx" (4)
Fs = k(0-x) = -kx (5)
Fd = d(x'-0) = dx' (6)
Substitueren van (5) en (6) in (4) geeft
-kx - dx' = mx"
Zoals je ziet, krijg je voor A en B dezelfde bewegingsvergelijking.
Als we x naar rechts als positief kiezen, dan geldt voor A:
-Fs + Fd = mx" (1)
Fs = k(x-0) = kx (2)
Fd = d(0-x') = -dx' (3)
Substitueren van de (2) en (3) in (1) geeft
-kx - dx' = mx"
We kiezen wederom x naar rechts als positief en dan vinden we voor B:
Fs - Fd = mx" (4)
Fs = k(0-x) = -kx (5)
Fd = d(x'-0) = dx' (6)
Substitueren van (5) en (6) in (4) geeft
-kx - dx' = mx"
Zoals je ziet, krijg je voor A en B dezelfde bewegingsvergelijking.
Hey,
Zou iemand me kunnen helpen met deze fysica vraag...
Een uniform verdeelde lading (lineaire ladingsdichtheid 9 nC/m) is geplaatst tussen x=0 en x=3 langsheen de x-as. Bereken de grootte van het elektrisch veld in x = 4.
ik begrijp dat ik de volgende formule moet gebruiken : Ke * ʃ 1/r^2 dq
Ke is een constante namelijk 8,99 *10^9 en dq mag voor het integraal teken gezet worden.
Dus Ke * q *ʃ 1/r^2
dan moet ʃ 1/r^2 omgezet worden naar de primitieve vorm.. ik kom dan uit op ʃ r^-1 /-1 en vervolgens ʃ - 1 / r ... Het is een bepaalde integraal met begin waarde 0 en eindwaarde 3.
Ik weet echter totaal niet hoe ik nu verder moet, ik snap dat ik met bovenstaande formule het electrisch veld moet berekenen tot x=3 en dan x=4 als puntlading moet beschouwen... maar het lukt me niet. Het zou fijn zijn als iemand me hiermee kan helpen !
Zou iemand me kunnen helpen met deze fysica vraag...
Een uniform verdeelde lading (lineaire ladingsdichtheid 9 nC/m) is geplaatst tussen x=0 en x=3 langsheen de x-as. Bereken de grootte van het elektrisch veld in x = 4.
ik begrijp dat ik de volgende formule moet gebruiken : Ke * ʃ 1/r^2 dq
Ke is een constante namelijk 8,99 *10^9 en dq mag voor het integraal teken gezet worden.
Dus Ke * q *ʃ 1/r^2
dan moet ʃ 1/r^2 omgezet worden naar de primitieve vorm.. ik kom dan uit op ʃ r^-1 /-1 en vervolgens ʃ - 1 / r ... Het is een bepaalde integraal met begin waarde 0 en eindwaarde 3.
Ik weet echter totaal niet hoe ik nu verder moet, ik snap dat ik met bovenstaande formule het electrisch veld moet berekenen tot x=3 en dan x=4 als puntlading moet beschouwen... maar het lukt me niet. Het zou fijn zijn als iemand me hiermee kan helpen !
Nee, dat mag niet. Als je docent of boek dat beweert is dat flauwekul. Bedenk eerst eens wat dq/dr is.quote:
Hey,
Zou iemand me kunnen helpen met deze fysica vraag...
Een uniform verdeelde lading (lineaire ladingsdichtheid 9 nC/m) is geplaatst tussen x=0 en x=3 langsheen de x-as. Bereken de grootte van het elektrisch veld in x = 4.
ik begrijp dat ik de volgende formule moet gebruiken : Ke * ʃ 1/r^2 dq
Ke is een constante namelijk 8,99 *10^9 en dq mag voor het integraal teken gezet worden.
hmm, ja ik dacht dat het integraal teken het differentiaalteken opheft en dat ik daarom q voor het integraalteken kan zetten. Maar om terug te komen op je vraag, dq/dr is volgens mij een heel klein deel van q gedeeld door een heel klein deel van r ..
Wat je in feite moet doen is de bijdrage aan het elektrisch veld van alle 'infinitesimale' ladingen dq verspreid over het lijnstuk langs de x-as van x = 0 tot x = 3 bij elkaar optellen. De bijdrage die één zo'n elementje levert is omgekeerd evenredig met het kwadraat van de afstand r tot het punt x = 4, en die afstand r loopt dus van r = 4 (voor x = 0) tot r = 1 (voor x = 3). Dan weet je dus al dat je moet integreren met r (niet q) als variabele en over het interval [1,4]. Weer de vraag: wat is dq/dr hier? Nu mag je het weer even zelf proberen.quote:
hmm, ja ik dacht dat het integraal teken het differentiaalteken opheft en dat ik daarom q voor het integraalteken kan zetten. Maar om terug te komen op je vraag, dq/dr is volgens mij een heel klein deel van q gedeeld door een heel klein deel van r ..
Het 1e deel van je uitleg snap ik wel, ik weet alleen niet precies wat dq/dr is... ik weet dat df/dx de 1e afgeleide is van de functie f. Ik denk dan dat dq/dr wil zeggen dat je q afleidt naar r ?? Dit deel snap ik niet echt, ik heb het proberen op te zoeken maar ik word er niet veel wijzer van..
Als ik er echter vanuit ga dat ik bij de formule: Ke * ʃ 1/r^2 dq.
dq niet voor het integraalteken mag zetten kom ik op t volgende uit: Ke * ʃ -q/r
als ik dan het interval [1,4] toepas kom ik uit op 60,75 en dat is het juiste antwoord. Maar wat dq/dr nou precies is en wat die dq inhoudt begrijp ik ook niet echt...
Als ik er echter vanuit ga dat ik bij de formule: Ke * ʃ 1/r^2 dq.
dq niet voor het integraalteken mag zetten kom ik op t volgende uit: Ke * ʃ -q/r
als ik dan het interval [1,4] toepas kom ik uit op 60,75 en dat is het juiste antwoord. Maar wat dq/dr nou precies is en wat die dq inhoudt begrijp ik ook niet echt...
Het is echt heel eenvoudig, want in de opgave staat dat de lading uniform is verdeeld over het lijnstuk en dat de lineaire ladingsdichtheid 9 nC/m bedraagt. Dus hebben we dq/dr = 9 nC/m = 9∙10-9 C/m.quote:
Het 1e deel van je uitleg snap ik wel, ik weet alleen niet precies wat dq/dr is... ik weet dat df/dx de 1e afgeleide is van de functie f. Ik denk dan dat dq/dr wil zeggen dat je q afleidt naar r ?? Dit deel snap ik niet echt, ik heb het proberen op te zoeken maar ik word er niet veel wijzer van..
Zoals gezegd integreer je met r als variabele, en dus moet je ook een integraal krijgen met dr, niet met dq.quote:Als ik er echter vanuit ga dat ik bij de formule: Ke * ʃ 1/r^2 dq.
dq niet voor het integraalteken mag zetten kom ik op t volgende uit: Ke * ʃ -q/r
als ik dan het interval [1,4] toepas kom ik uit op 60,75 en dat is het juiste antwoord. Maar wat dq/dr nou precies is en wat die dq inhoudt begrijp ik ook niet echt...
Welnu, voor de bijdrage dE aan het electrisch veld van een 'infinitesimale' lading dq op een stukje dr van het lijnstuk op een afstand r van het punt x = 4 hebben we:
dE = Ke∙r-2∙dq
Maar nu weten we ook dat dq/dr = 9∙10-9 C/m en dus dq = 9∙10-9∙dr (Coulomb, aangezien r in meter wordt uitgedrukt). Dus krijgen we:
dE = Ke∙r-2∙9∙10-9∙dr = 9∙10-9∙Ke∙r-2∙dr
De veldsterkte E in het punt x = 4 door de lading op het lijnstuk L wordt nu:
E = ʃL dE = 9∙10-9∙Ke∙ʃ14 r-2∙dr = 9∙10-9∙Ke∙[-r-1]14 = 9∙10-9∙Ke∙((-1/4) - (-1)) = 9∙10-9∙Ke∙(3/4) ≈ 60,75 N/C.
[ Bericht 2% gewijzigd door Riparius op 21-06-2012 13:15:58 ]
haha ja ik zie nu wat je bedoelt met dq/dr, en ik begrijp je werkwijze. Maar we komen op t zelfde antwoord uit, en ik gebruik deze formule Ke * ʃ -q/r. Volgens mij klopt deze formule dan ook of zie ik hier toch weer iets over t hoofd ?
Heel erg bedankt voor je uitleg, het is een stuk duidelijker nu !
Heel erg bedankt voor je uitleg, het is een stuk duidelijker nu !
Nee, je formule klopt niet. Om te beginnen is -r-1 een primitieve van r-2, dus moet je dan niet meer dat integraalteken schrijven. Hierboven deed je dat ook al, en dat is gewoon fout. Correct is bijvoorbeeld wel:quote:
Haha ja ik zie nu wat je bedoelt met dq/dr, en ik begrijp je werkwijze. Maar we komen op 't zelfde antwoord uit, en ik gebruik deze formule Ke * ʃ -q/r. Volgens mij klopt deze formule dan ook of zie ik hier toch weer iets over 't hoofd ?
∫14 r-2dr = [-r-1]14 = (-1/4) -(-1) = 3/4.
Je hebt wel gelijk dat d en ∫ inverse bewerkingen symboliseren, zodat bijvoorbeeld E = ∫ dE, en zo heb je ook q = ∫ dq, maar je moest de veldsterkte E berekenen in het punt x = 4, en niet de lading q van het gehele lijnstuk. Dus moet je eerst een uitdrukking voor dE afleiden, zoals ik hierboven heb gedaan.
quote:Heel erg bedankt voor je uitleg, het is een stuk duidelijker nu !
Help! Morgen een tentamen moleculaire biologie maar er is een techniek die ik echt niet snap. 
Het gaat om het gebruiken van homologe recombinatie om knock outs te maken (in bv. muisjes).
Als iemand me dit wat duidelijker kan uitleggen of een goed filmpje weet waarin de techniek wordt besproken zou ik dat erg op prijs stellen.
Het gaat om het gebruiken van homologe recombinatie om knock outs te maken (in bv. muisjes).
Als iemand me dit wat duidelijker kan uitleggen of een goed filmpje weet waarin de techniek wordt besproken zou ik dat erg op prijs stellen.
Wat snap je niet precies?quote:
Help! Morgen een tentamen moleculaire biologie maar er is een techniek die ik echt niet snap.
Het gaat om het gebruiken van homologe recombinatie om knock outs te maken (in bv. muisjes).
Als iemand me dit wat duidelijker kan uitleggen of een goed filmpje weet waarin de techniek wordt besproken zou ik dat erg op prijs stellen.
Ik heb hier een vraag over de impulsbalans van een vak genaamd Fysische Transportverschijnselen. Het gaat om stroming van een vloeistof door een buis. De opdracht is geformuleerd als volgt:
De eerste 2 vragen kan op oplossen. a wordt opgelost door het opstellen van een massabalans, en b door het opstellen van een energiebalans. Ik weet dat vraag c wordt opgelost door het opstellen van een impulsbalans, maar ik begrijp het zelf niet echt. Ik heb hier een gedeelte van de uitwerking door de docent.
Dit is de algemene impulsbalans, dat is het makkelijke gedeelte:
Echter ik begrijp niet waarom deze kracht negatief is, en waarom niet cosinus of tangens.
Weet iemand hier het antwoord op?
De eerste 2 vragen kan op oplossen. a wordt opgelost door het opstellen van een massabalans, en b door het opstellen van een energiebalans. Ik weet dat vraag c wordt opgelost door het opstellen van een impulsbalans, maar ik begrijp het zelf niet echt. Ik heb hier een gedeelte van de uitwerking door de docent.
Dit is de algemene impulsbalans, dat is het makkelijke gedeelte:
Echter ik begrijp niet waarom deze kracht negatief is, en waarom niet cosinus of tangens.
Weet iemand hier het antwoord op?
In de onderste tekening is v3 ontbonden in een x- en y-component en daarbij wijst de y-component omlaag. Omdat die y-component omlaag wijst en y omhoog als positief is gedefinieerd, moet de y-component van v3 negatief zijn.quote:
Ik heb hier een vraag over de impulsbalans van een vak genaamd Fysische Transportverschijnselen. Het gaat om stroming van een vloeistof door een buis. De opdracht is geformuleerd als volgt:
[ afbeelding ]
De eerste 2 vragen kan op oplossen. a wordt opgelost door het opstellen van een massabalans, en b door het opstellen van een energiebalans. Ik weet dat vraag c wordt opgelost door het opstellen van een impulsbalans, maar ik begrijp het zelf niet echt. Ik heb hier een gedeelte van de uitwerking door de docent.
Dit is de algemene impulsbalans, dat is het makkelijke gedeelte:
[ afbeelding ]
Echter ik begrijp niet waarom deze kracht negatief is, en waarom niet cosinus of tangens.
[ afbeelding ]
[ afbeelding ]
Weet iemand hier het antwoord op?
Ik kom er maar niet uit hoe ik formules als om moet zetten naar bijvoorbeeld
Iemand die me dit uit kan leggen?
Iemand die me dit uit kan leggen?
Deel beide kanten door l, en doe dan beide kanten keer A. Wat komt daar dan uit?quote:
Ik kom er maar niet uit hoe ik formules als [ afbeelding ] om moet zetten naar bijvoorbeeld [ afbeelding ]
Iemand die me dit uit kan leggen?
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |