[Bèta wiskunde] Huiswerk- en vragentopic

Index

» school, studie en onderwijs

actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
pi_111490692
quote:
0s.gif Op zondag 13 mei 2012 14:15 schreef Amoeba het volgende:
Ik heb wel WisD, maar ook rijen is al een jaar terug. Ik heb dit jaar WisB gedaan (in 2 jaar) en volgend jaar WisD (dus ook in 2 jaar, omdat ik dit jaar geen WisD gedaan heb)

En jawel, ook die rotzooi stond in m'n GR :')

Maargoed, dat k=2, is dat het onderste limiet?
Die 5, staat dat voor het aantal rechthoeken -1?
k=2 is de eerste term in de som, k=5 de laatste in dat geval. Niet per se aantal rechthoeken -1.
pi_111490767
Maargoed, stel dat ik een functie van x = 2 tot x= 12 wil sommeren met een stapgrootte van 1/2

Dan zou ik:

x=2 -> x=11 moeten nemen, en in de somnotatie:
Y1(2+0.5k)*0.5

Daarbij moeten zetten?
pi_111490821
Ja, maar welke waardes nemen k dan precies aan in die som?
pi_111490859
Geen idee wat je zojuist zei. Verklaar je nader.

Ik wil gewoon een integraal uit kunnen drukken (benaderen) met een Riemannsom, op de manier van een somrij. Stel dat zo'n rotvraag komt in het examen, dan wil ik die toch graag op kunnen lossen.
pi_111490889
Ik heb het net al een keer voorgedaan, dus nu mag jij.
pi_111490931
quote:
0s.gif Op zondag 13 mei 2012 13:19 schreef thenxero het volgende:
Op Thabits manier krijg je een bovensom en ondersom (dus een bovengrens en ondergrens voor de integraal). Je kan ook steeds op ieder interval [xk, xk+1] de waarden in het midden nemen en daar f evalueren. Dan krijg je iets wat direct wat dichter bij de integraal zal zitten dan de ondersom of bovensom, en het is ook wat makkelijker te berekenen omdat je niet het supremum of infimum op ieder intervalletje hoeft te bepalen (dan moet je steeds nagaan of de functie daalt of stijgt op dat interval, etc).

Voorbeeld: Je moet het interval [2,24] opdelen in kleine deelintervalletjes. Je kan als grootte van die deelintervalletjes bijvoorbeeld 1 nemen (hoe kleiner, hoe dichter je bij de werkelijke integraal komt). Als je f dan steeds op de middens van die deelintervalletjes evalueert, moet je dus het volgende berekenen:
\sum_{k=2}^{23} f(k+\frac{1}{2})\cdot 1=\sum_{k=2}^{23} 3^{k+\frac{1}{2}}-9(k+\frac{1}{2})\approx 2.44\cdot10^{11}

Terwijl
\int_2^{24} 3^x - 9x\,dx\approx 2.57 \cdot 10^{11}

Dus dat zit nog redelijk in de buurt, ondanks het feit dat ik zulke grote deelintervallen heb genomen en je functie zo ontzettend hard stijgt ;) .
Dit is nice, maar hoe moet het met een interval van 0.1?
pi_111491080
quote:
0s.gif Op zondag 13 mei 2012 14:23 schreef thenxero het volgende:
Ik heb het net al een keer voorgedaan, dus nu mag jij.


?
pi_111491117
Ik heb wel echt het gevoel dat hier geen fuck van klopt.
pi_111491345
quote:
0s.gif Op zondag 13 mei 2012 13:50 schreef jabbahabba het volgende:

[..]

hij zit grappig te doen, hij streept de n van sin(x) weg
Is dat niet goed dan :?
pi_111491432
quote:
14s.gif Op zondag 13 mei 2012 14:35 schreef PizzaGeit het volgende:

[..]

Is dat niet goed dan :?
Nee, als je dit had gezegd was het wel goed geweest:
\frac{\sin x}{n} = ?
six=?
?=6

Volgende keer beter :P
pi_111491466
quote:
12s.gif Op zondag 13 mei 2012 14:37 schreef thenxero het volgende:

[..]

Nee, als je dit had gezegd was het wel goed geweest:
\frac{\sin x}{n} = ?
six=?
?=6

Volgende keer beter :P
:')
pi_111491545
quote:
0s.gif Op zondag 13 mei 2012 14:28 schreef Amoeba het volgende:

[..]

[ afbeelding ]

?
Je moet geen { } haken gebruiken. Daardoor gaat wolframalhpa de mist in.

Je begin en eindwaardes van k kloppen niet. Waarom heb je die zo gekozen?
pi_111491590
quote:
12s.gif Op zondag 13 mei 2012 14:37 schreef thenxero het volgende:

[..]

Nee, als je dit had gezegd was het wel goed geweest:
\frac{\sin x}{n} = ?
six=?
?=6

Volgende keer beter :P
Oh ;(
pi_111491683


Dit is dan ook weer niet goed zeker ;(
pi_111491687
[tex]
quote:
0s.gif Op zondag 13 mei 2012 14:40 schreef thenxero het volgende:

[..]

Je moet geen { } haken gebruiken. Daardoor gaat wolframalhpa de mist in.

Je begin en eindwaardes van k kloppen niet. Waarom heb je die zo gekozen?
Omdat ik het interval van 2 tot 24 wilde..

Xk klopt wel?
pi_111491915
quote:
14s.gif Op zondag 13 mei 2012 14:44 schreef PizzaGeit het volgende:
[ afbeelding ]

Dit is dan ook weer niet goed zeker ;(
Ziet er prima uit hoor.
quote:
0s.gif Op zondag 13 mei 2012 14:44 schreef Amoeba het volgende:
[tex]

[..]

Omdat ik het interval van 2 tot 24 wilde..

Xk klopt wel?
Als je sommeert van k=2 tot k=24, dan is dus je het eerste midden van de deelintervalletjes bij 2+0.5*2 = 3, en de laatste bij 2+0.5*24 = 14. Je "integreert" dus eigenlijk van 2.75 tot 14.25 op deze manier.
pi_111492193
Ah, oke.

Xk = Xbeginwaarde +stapgrootte*k
a en b zou ik dan zo uit moeten drukken dat de Xk * k = a (die waarde van k dus), evenals voor b?

Zit ik zo goed? :P
pi_111492436
Zoiets...

xk = linkergrens + (de helft van de stapgrootte) + (stapgrootte * k)

En dan sommeren van k=0 tot k zodanig dat x_k = (rechtergrens - de helft van de stapgrootte).

Of anders gezegd: Als linkergrens a heet, en rechtergrens b, dan laat je k zo lopen dat je (b-a)/(stapgrootte) termen krijgt.
pi_111492554
[tex]\sum_{k=30}^{70} (3(2+1/10k)-2(2+1/10k)^2) \cdot 1/10[/tex]

Stel dat ik wil gaan van x=5 tot x=10
Functie: 3x - 2x^2
Stapgrootte: 1/10

Dan is dit fout. Laat het me nogmaals proberen..

[ Bericht 43% gewijzigd door #ANONIEM op 13-05-2012 15:09:18 ]
pi_111492679
\sum_{k=0}^{50} (3(2,05+1/10k)-2(2,05+1/10k)^2) \cdot 1/10

Stel dat ik wil gaan van x=5 tot x=10
Functie: 3x - 2x^2
Stapgrootte: 1/10

Zo?
pi_111492757
Maar het komt absoluut niet overeen met de integraal...
pi_111492794
Integreer eens van 2 tot 7.1, en kijk wat er gebeurt :P .
pi_111492906
Maar die onderste, moet die in dit geval 0 zijn? Of iets van 30?

Edit: Ik heb die integraal bekeken.

Moet k van 30 tot 80 lopen?

[ Bericht 40% gewijzigd door #ANONIEM op 13-05-2012 15:21:05 ]
pi_111493053
Dan is je beginwaarde 5.05 (OK) en je eindwaarde 10.05 (niet OK), het laatste midden van je rechthoek zit bij 9.95
pi_111493081
Dan 79.
pi_111493129
Inderdaad. Je had ook gewoon xk = 5.05 + k/10 kunnen nemen, en dan sommeren van k=0 tot k=49 . Maar dat komt op hetzelfde neer.

Komt het nu wel mooi overeen met de integraal?
pi_111493131
\sum_{k=30}^{79} (3(2,05+1/10k)-2(2,05+1/10k)^2) \cdot 1/10
pi_111493182
Ohja, ik zie nu pas dat ik dat had moeten doen, aangezien ik net de hele tijd vanaf x=2 nam etc. :')
Maargoed, dan geldt dus dit:

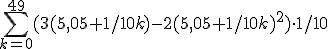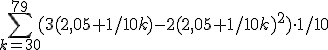
\sum_{k=0}^{49} (3(5,05+1/10k)-2(5,05+1/10k)^2) \cdot 1/10 = \sum_{k=30}^{79} (3(2,05+1/10k)-2(2,05+1/10k)^2) \cdot 1/10
pi_111493332
Precies. Kies je favoriete som ;) . Wat komt eruit? En wat komt er uit de integraal?
pi_111493519
-470,825 bij de somrij
-470,833 bij de integraal.

Hoe lost je GR eigenlijk een integraal op, een somrij toch gewoon?
Mijn primitieve komt uit op -2025/6 Hetzelfde als de integraal dus.
actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
[Bèta wiskunde] Huiswerk- en vragentopic
Index

» school, studie en onderwijs

Forum Opties
Forumhop:
Hop naar:
(afkorting, bv 'KLB')