SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Dat haal je uit de eenheid van de snelheid. De formule voor de tijd is t=s/v, als je de afstand in meters (m) hebt en de snelheid in meters per seconde (m/s), krijg je de tijd in seconden. Dat kan je zelf ook nagaan, vul de eenheden maar in in de formule: [t]=[s]/[v]=m/(m/s)=s. In deze notatie staat [t] voor de eenheid van tijd (in dit geval dus seconden).quote:Op woensdag 29 februari 2012 22:13 schreef datisstom het volgende:
En als je nou tijd berekent, hoe weet je dan welke eenheid je hebt berekend?
The biggest argument against democracy is a five minute discussion with the average voter.


Bedankt, het is allemaal een stuk duidelijker nu ik wat slaap heb gehad.quote:Op woensdag 29 februari 2012 22:23 schreef M.rak het volgende:
[..]
Dat haal je uit de eenheid van de snelheid. De formule voor de tijd is t=s/v, als je de afstand in meters (m) hebt en de snelheid in meters per seconde (m/s), krijg je de tijd in seconden. Dat kan je zelf ook nagaan, vul de eenheden maar in in de formule: [t]=[s]/[v]=m/(m/s)=s. In deze notatie staat [t] voor de eenheid van tijd (in dit geval dus seconden).
Edit: bij nader inzien; 25 km / 10 m per seconde is 2,5 seconden.
[ Bericht 12% gewijzigd door datisstom op 01-03-2012 16:03:49 ]


Dat kan natuurlijk sowieso nooit, als je iedere seconde 10 meter aflegt, heb je in 2.5 seconden geen 10 km afgelegdquote:Op donderdag 1 maart 2012 15:54 schreef datisstom het volgende:
[..]
Bedankt, het is allemaal een stuk duidelijker nu ik wat slaap heb gehad.
Edit: bij nader inzien; 25 km / 10 m per seconde is 2,5 seconden.

The biggest argument against democracy is a five minute discussion with the average voter.


Ja maar hoe weet je dan naar welke eenheid je om moet rekenen? Km/s kan toch ook gewoon? Maar 2,5 km/s kan dus duidelijk niet.


Ik zie het probleem niet zo eigenlijk 
snelheid: eenheid van afstand (L) / eenheid van tijd (T)
afstand: eenheid van afstand (L)
tijd: eenheid van tijd (T)
Nu moet je ervoor zorgen dat je voor de eenheid van afstand en voor de eenheid van tijd overal hetzelfde kiest. Kwestie van dimensieanalyse toepassen.
Als je zeker van je zaak wilt zijn reken je alles gewoon om naar SI-eenheden. Voor afstand is dat meters, voor tijd is dat seconden. Voor snelheid is het dan logischerwijs meter per seconde in SI.
Jouw voorbeeld:
25km -> 25.000 meter (SI)
10 m/s -> 10 m/s (SI)
Formule toepassen: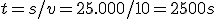
Achteraf kun je nog altijd omrekenen naar een andere eenheid indien dat gevraagd/nodig is.
snelheid: eenheid van afstand (L) / eenheid van tijd (T)
afstand: eenheid van afstand (L)
tijd: eenheid van tijd (T)
Nu moet je ervoor zorgen dat je voor de eenheid van afstand en voor de eenheid van tijd overal hetzelfde kiest. Kwestie van dimensieanalyse toepassen.
Als je zeker van je zaak wilt zijn reken je alles gewoon om naar SI-eenheden. Voor afstand is dat meters, voor tijd is dat seconden. Voor snelheid is het dan logischerwijs meter per seconde in SI.
Jouw voorbeeld:
25km -> 25.000 meter (SI)
10 m/s -> 10 m/s (SI)
Formule toepassen:
Achteraf kun je nog altijd omrekenen naar een andere eenheid indien dat gevraagd/nodig is.


Vraag je voor mijn PO Natuurkunde,
Ik heb deze twee proeven gekregen:
Proef 1:
http://www.natuurkunde.nl(...)d=3&supportId=588151
^Het lijkt hierop.
De stippellijn is bij ons een statief, de hoek is niet gegeven, lengte van het touw was bij ons ook niet gegeven, het zwarte blokje waren bij ons 3 gewichtjes en de kracht naar rechts hebben we gemeten met een veerunster.
Nu moet ik voor mijn PO een hoofdstuke maken met meetfouten et cetera.
Maar ik weet niet precies wat voor onnauwkeurigheden ik hier gemaakt zou kunnen hebben.
Ik dacht zelf aan:
- Fout bij het meten van de hoek
- Fout bij het aflezen van de veerunster
- De veerunster niet helemaal horizontaal houden
Zijn er nog andere 'fouten' die bij deze proef veel voorkomend zijn?
-----
En dan nu proef 2 nog.
Deze leek een beetje hierop:
De driehoek bestaat uit een statief en een soort van 'rails' waar je een karretje op kan zetten. (hier afgebeeld als een rondje) bij ons ging het touwtje echter via de katrol omhoog en zat daar vast aan een veerunster. En dan moesten we verschillende hellingshoeken uitproberen en verschillend extra gewicht (aan het karretje vast), om te kijken hoeveel kracht er nodig was om het karretje op z'n plaats te houden.
Hierbij dacht ik aan deze mogelijke fouten:
- Onnauwkeurig aflezen van de veerunster
- De hellingshoek niet op de graad perfect afgemeten
Zijn er hier ook nog andere veel voorkomende 'fouten'?
Alvast bedankt voor jullie hulp.
Ik heb deze twee proeven gekregen:
Proef 1:
http://www.natuurkunde.nl(...)d=3&supportId=588151
^Het lijkt hierop.
De stippellijn is bij ons een statief, de hoek is niet gegeven, lengte van het touw was bij ons ook niet gegeven, het zwarte blokje waren bij ons 3 gewichtjes en de kracht naar rechts hebben we gemeten met een veerunster.
Nu moet ik voor mijn PO een hoofdstuke maken met meetfouten et cetera.
Maar ik weet niet precies wat voor onnauwkeurigheden ik hier gemaakt zou kunnen hebben.
Ik dacht zelf aan:
- Fout bij het meten van de hoek
- Fout bij het aflezen van de veerunster
- De veerunster niet helemaal horizontaal houden
Zijn er nog andere 'fouten' die bij deze proef veel voorkomend zijn?
-----
En dan nu proef 2 nog.
Deze leek een beetje hierop:
De driehoek bestaat uit een statief en een soort van 'rails' waar je een karretje op kan zetten. (hier afgebeeld als een rondje) bij ons ging het touwtje echter via de katrol omhoog en zat daar vast aan een veerunster. En dan moesten we verschillende hellingshoeken uitproberen en verschillend extra gewicht (aan het karretje vast), om te kijken hoeveel kracht er nodig was om het karretje op z'n plaats te houden.
Hierbij dacht ik aan deze mogelijke fouten:
- Onnauwkeurig aflezen van de veerunster
- De hellingshoek niet op de graad perfect afgemeten
Zijn er hier ook nog andere veel voorkomende 'fouten'?
Alvast bedankt voor jullie hulp.


Je verwaarloost de weerstand van de katrol, dat is ook een onnauwkeurigheid.quote:Op donderdag 8 maart 2012 16:34 schreef Miraculously het volgende:
Vraag je voor mijn PO Natuurkunde,
Ik heb deze twee proeven gekregen:
-----
En dan nu proef 2 nog.
Deze leek een beetje hierop:
[ afbeelding ]
De driehoek bestaat uit een statief en een soort van 'rails' waar je een karretje op kan zetten. (hier afgebeeld als een rondje) bij ons ging het touwtje echter via de katrol omhoog en zat daar vast aan een veerunster. En dan moesten we verschillende hellingshoeken uitproberen en verschillend extra gewicht (aan het karretje vast), om te kijken hoeveel kracht er nodig was om het karretje op z'n plaats te houden.
Hierbij dacht ik aan deze mogelijke fouten:
- Onnauwkeurig aflezen van de veerunster
- De hellingshoek niet op de graad perfect afgemeten
Zijn er hier ook nog andere veel voorkomende 'fouten'?
Alvast bedankt voor jullie hulp.


Oké, bedankt.quote:Op donderdag 8 maart 2012 16:38 schreef Jochemz het volgende:
[..]
Je verwaarloost de weerstand van de katrol, dat is ook een onnauwkeurigheid.
Dan zal ik dat er ook bij verwerken.


Weet iemand misschien iets om de meetnauwkeurigheid te verhogen, en dan doel ik op de katrol, dus die vervangen of een of ander trucje toepassen waardoor de weerstand zo klein mogelijk wordt.
Zelf hadden we al het karretje iets omlaag getrokken en losgelaten om de weerstand te verminderen.
Zijn hier nog andere opties voor?
En dan heb ik nog een klein vraagje, in mijn opdracht staat dit:
'Bereken met behulp van de hellingshoek en het gewicht van het karretje de component van de zwaartekracht op het karretje langs het vlak en vergelijk deze met de gementen kracht'
Dat is dan toch m * g * sin(hoek)
Of heb ik het nu fout?
[ Bericht 32% gewijzigd door Miraculously op 08-03-2012 17:32:16 ]
Zelf hadden we al het karretje iets omlaag getrokken en losgelaten om de weerstand te verminderen.
Zijn hier nog andere opties voor?
En dan heb ik nog een klein vraagje, in mijn opdracht staat dit:
'Bereken met behulp van de hellingshoek en het gewicht van het karretje de component van de zwaartekracht op het karretje langs het vlak en vergelijk deze met de gementen kracht'
Dat is dan toch m * g * sin(hoek)
Of heb ik het nu fout?
[ Bericht 32% gewijzigd door Miraculously op 08-03-2012 17:32:16 ]


Tuurlijk, er zit allebei een ij in, maar dit lijkt me niet helemaal het juist topicquote:Op donderdag 8 maart 2012 21:41 schreef TheOnion het volgende:
Waar is de alfa huiswerk vragen topic? Dan maar hier
Is mij en mijn ook assonantie?
Ontopic: als je een deelruimte van R3 hebt, bijvoorbeeld:
{(1, a, b)t : a,b uit R}
Mag je deze dan beschrijven als: de deelruimte van R3 die wordt opgespannen door (0, 1, 0)t en (0, 0, 1)t en (1, 0, 0)t bevat?


Daarvoor kan je beter in het wiskunde huiswerk- en vragentopic zijn denk ikquote:Op vrijdag 9 maart 2012 23:44 schreef kutkloon7 het volgende:
[..]
Tuurlijk, er zit allebei een ij in, maar dit lijkt me niet helemaal het juist topic.
Ontopic: als je een deelruimte van R3 hebt, bijvoorbeeld:
{(1, a, b)t : a,b uit R}
Mag je deze dan beschrijven als: de deelruimte van R3 die wordt opgespannen door (0, 1, 0)t en (0, 0, 1)t en (1, 0, 0)t bevat?
The biggest argument against democracy is a five minute discussion with the average voter.


Dat is helemaal geen deelruimte!quote:Op vrijdag 9 maart 2012 23:44 schreef kutkloon7 het volgende:
[..]
Tuurlijk, er zit allebei een ij in, maar dit lijkt me niet helemaal het juist topic.
Ontopic: als je een deelruimte van R3 hebt, bijvoorbeeld:
{(1, a, b)t : a,b uit R}
Mag je deze dan beschrijven als: de deelruimte van R3 die wordt opgespannen door (0, 1, 0)t en (0, 0, 1)t en (1, 0, 0)t bevat?


Zit ik een beetje stoer te doen, met mijn ontopic... Haha, ik dacht dat dit het wiskundetopic was, sorryquote:Op vrijdag 9 maart 2012 23:49 schreef M.rak het volgende:
[..]
Daarvoor kan je beter in het wiskunde huiswerk- en vragentopic zijn denk ik. Maar als antwoord op je vraag, dat lijkt me niet, het opspansel wat jij geeft is namelijk de hele R3. Je kan het wel schrijven als (1,0,0)t plus het opspansel van (0, 1, 0)t en (0, 0, 1)t. Maar er zijn misschien handigere manieren om dat op te schrijven.
Verder bedoelde ik (ik had het iets duidelijker moeten verwoorden denk ik):
de deelruimte van R3 die wordt opgespannen door (0, 1, 0)t en (0, 0, 1)t,
en het punt (1, 0, 0) bevat. Maar dit mag dus niet, omdat de deelruimte die wordt opgespannen door (0, 1, 0) en (0, 0, 1) al per definitie (1, 0, 0) niet bevat?


Ik moet voor mijn studie een programma schrijven dat, gegeven een ongerichte gewogen graaf, een verzameling kanten geeft die, als je deze verwijdert, de graaf in twee componenten split. Er worden twee knopen gegeven die in een verschillend component moeten zitten. Dit heet een min-cut vinden (en is gerelateerd aan een max-flow vinden), en kan met de Ford-Fulkerson-methode.
Dit heb ik geïmplementeerd, maar volgens het automatische inleverprogramma geeft mijn programma nog het foute antwoord op sommige testinvoeren. Er is verder slechts een kleine voorbeeld in- en output beschikbaar, waar mijn programma wel gewoon de goede output voor levert. Ook op elke testinvoer die ik zelf bedenk levert mijn programma de goede output. Heeft iemand een idee wat ik nu kan doen? Ik heb het programma al een paar keer opnieuw geschreven, met hetzelfde resultaat.
Dit heb ik geïmplementeerd, maar volgens het automatische inleverprogramma geeft mijn programma nog het foute antwoord op sommige testinvoeren. Er is verder slechts een kleine voorbeeld in- en output beschikbaar, waar mijn programma wel gewoon de goede output voor levert. Ook op elke testinvoer die ik zelf bedenk levert mijn programma de goede output. Heeft iemand een idee wat ik nu kan doen? Ik heb het programma al een paar keer opnieuw geschreven, met hetzelfde resultaat.


Het programma hier posten en hopen dat iemand zin heeft om ernaar te kijken.quote:Op maandag 2 april 2012 18:34 schreef kutkloon7 het volgende:
Ik moet voor mijn studie een programma schrijven dat, gegeven een ongerichte gewogen graaf, een verzameling kanten geeft die, als je deze verwijdert, de graaf in twee componenten split. Er worden twee knopen gegeven die in een verschillend component moeten zitten. Dit heet een min-cut vinden (en is gerelateerd aan een max-flow vinden), en kan met de Ford-Fulkerson-methode.
Dit heb ik geïmplementeerd, maar volgens het automatische inleverprogramma geeft mijn programma nog het foute antwoord op sommige testinvoeren. Er is verder slechts een kleine voorbeeld in- en output beschikbaar, waar mijn programma wel gewoon de goede output voor levert. Ook op elke testinvoer die ik zelf bedenk levert mijn programma de goede output. Heeft iemand een idee wat ik nu kan doen? Ik heb het programma al een paar keer opnieuw geschreven, met hetzelfde resultaat.


Ik heb nog even verder gekeken, en met code die ik op internet heb gevonden heb ik even een geautomatiseerd testomgevinkje in elkaar gezet. De maxflow wordt hoogstwaarschijnlijk gewoon goed berekend, in elk geval heb ik in 10000+ random gevallen nog geen afwijking van de code op internet gevonden.
Dus dan zou het of een fout in het automatisch nakijken van het practicum moeten zijn, een fout bij het gedeelte na het berekenen van de maxflow, of een fout die alleen voorkomt in een randgeval. Ik ga het gewoon aan de practicumleider vragen, die kan hopelijk wel bij de in- en output van mijn programma, want ik geloof niet dat er zo iets anders op zit.
Ik zou natuurlijk mijn code kunnen posten, maar er wordt automatisch gecontroleerd op fraude (ook op internet, zo is me verteld), en eerlijk gezegd denk ik niet dat het veel gaat helpen, aangezien mijn programma in alle testcases die ik gebruikt heb gewoon het goede antwoord geeft. Bovendien is het een behoorlijke lap tekst die niet al te elegant en begrijpelijk is geschreven (het was de 6e keer dat ik het programma overnieuw schreef, dan heb je een beetje schijt aan variabelennamen enzo).
Update:
Het is inmiddels gelukt, er was een waarde < 231. Ik dacht dat ik deze in een int kon opslaan, wat ook zo was, maar door de manier waarop ik de waarden opsloeg werd deze groter. Ik gebruik nu een uint en dat werkt .
.
[ Bericht 7% gewijzigd door kutkloon7 op 04-04-2012 11:29:25 ]
Dus dan zou het of een fout in het automatisch nakijken van het practicum moeten zijn, een fout bij het gedeelte na het berekenen van de maxflow, of een fout die alleen voorkomt in een randgeval. Ik ga het gewoon aan de practicumleider vragen, die kan hopelijk wel bij de in- en output van mijn programma, want ik geloof niet dat er zo iets anders op zit.
Ik zou natuurlijk mijn code kunnen posten, maar er wordt automatisch gecontroleerd op fraude (ook op internet, zo is me verteld), en eerlijk gezegd denk ik niet dat het veel gaat helpen, aangezien mijn programma in alle testcases die ik gebruikt heb gewoon het goede antwoord geeft. Bovendien is het een behoorlijke lap tekst die niet al te elegant en begrijpelijk is geschreven (het was de 6e keer dat ik het programma overnieuw schreef, dan heb je een beetje schijt aan variabelennamen enzo).
Update:
Het is inmiddels gelukt, er was een waarde < 231. Ik dacht dat ik deze in een int kon opslaan, wat ook zo was, maar door de manier waarop ik de waarden opsloeg werd deze groter. Ik gebruik nu een uint en dat werkt
[ Bericht 7% gewijzigd door kutkloon7 op 04-04-2012 11:29:25 ]


Hallo allemaal,
Voor biologie moet ik een artikel schrijven over een proefje met groenten. Ik heb gekozen om het volgende te doen:
Ik heb 5 porties van 25 gram tuinbonen, die ik 5 minuten kook. Ik heb 5 oplossingen, een van 0 gram NaCl per liter, een van 5 g/L, 10 g/L, 15 g/L en 20 g/L. In elk van de oplossingen kook ik dus één portie tuinbonen. Na het koken, meet ik met een spectrometer de kleur van het gekookte water. De kleur van het water verandert omdat er chlorofyl vrijkomt. Mijn hypothese was dat elke oplossing dezelfde pieken en dalen zou hebben, omdat chlorofyl te groot is om door osmose in het water te komen, en omdat alles even lang kookt, zou er gewoon even veel chlorofyl uit de kapotte cellen moeten komen. Maar nu blijkt dat er echt verschil zit tussen de oplossingen, en ik kan geen verklaring vinden waarom het zout er effect op heeft.
Alvast heel erg bedankt voor de hulp!
Voor biologie moet ik een artikel schrijven over een proefje met groenten. Ik heb gekozen om het volgende te doen:
Ik heb 5 porties van 25 gram tuinbonen, die ik 5 minuten kook. Ik heb 5 oplossingen, een van 0 gram NaCl per liter, een van 5 g/L, 10 g/L, 15 g/L en 20 g/L. In elk van de oplossingen kook ik dus één portie tuinbonen. Na het koken, meet ik met een spectrometer de kleur van het gekookte water. De kleur van het water verandert omdat er chlorofyl vrijkomt. Mijn hypothese was dat elke oplossing dezelfde pieken en dalen zou hebben, omdat chlorofyl te groot is om door osmose in het water te komen, en omdat alles even lang kookt, zou er gewoon even veel chlorofyl uit de kapotte cellen moeten komen. Maar nu blijkt dat er echt verschil zit tussen de oplossingen, en ik kan geen verklaring vinden waarom het zout er effect op heeft.
Alvast heel erg bedankt voor de hulp!
Ik houd je in de gaten...


Ik ben ook nog even aan het zoeken en denken, maar 1 oorzaak van je resultaten zou kunnen zijn dat er verschillende soorten chlorofyl bestaan. Elk soort chlorofyl heeft ook een andere absorptiepiek in het spectrum.
Het zout zorgt vooral voor een andere osmotische waarde.
0,9 massa% NaCl is de standaard voor een isotone oplossing. Dat zou zijn 9 gram in 1 liter water. Voor planten weet ik niet zeker of dit dezelfde waarde is.
5 g/L is dan in ieder geval hypotoon
10 g/L is dan ongeveer isotoon
15 en 20 g/L zijn dan hypertoon
Omdat er een andere turgordruk is, zou je ook kunnen verwachten dat de celwanden op een ander moment kapot gaan.
Maar bedoel je met een verschil in pieken en dalen dat de pieken op een andere plaats zitten? Of dat de hoogte van deze pieken/dalen anders is?
Het zout zorgt vooral voor een andere osmotische waarde.
0,9 massa% NaCl is de standaard voor een isotone oplossing. Dat zou zijn 9 gram in 1 liter water. Voor planten weet ik niet zeker of dit dezelfde waarde is.
5 g/L is dan in ieder geval hypotoon
10 g/L is dan ongeveer isotoon
15 en 20 g/L zijn dan hypertoon
Omdat er een andere turgordruk is, zou je ook kunnen verwachten dat de celwanden op een ander moment kapot gaan.
Maar bedoel je met een verschil in pieken en dalen dat de pieken op een andere plaats zitten? Of dat de hoogte van deze pieken/dalen anders is?
www.4beta.nl
www.youtube.nl/jweckhardt
---
Als je het niet simpel kunt uitleggen, begrijp je het niet goed genoeg
www.youtube.nl/jweckhardt
---
Als je het niet simpel kunt uitleggen, begrijp je het niet goed genoeg


Hee, we meet again, haha
Over het algemeen zijn chlorofyl a en chlorofyl b de meest voorkomende soorten, dat wist ik al, maar ik dacht dat als ik steeds dezelfde soort, en dezelfde portie bonen gebruik, dat dan dezelfde grafiek zou ontstaan. Over die pieken en dalen, ze zitten vooral op een andere hoogte, zie het plaatje
(0 g/L = rood; 5 g/L = blauw; 10 g/L = paars; 15 g/L = oranje; 20 g/L = groen; en er is geen rode lijn te zien omdat hij precies samenvalt met de blauwe)
http://www.filedropper.com/scheikundeallegrafieken
ik vond zelf dat de groene lijn erg lijkt op het absorptiespectrum van chlorofyl a en chlorofyl b
http://commons.wikimedia.org/wiki/File:Chlorophyll_ab_spectra.png
Ik vind je theorie eigenlijk wel heel logisch klinken, maar als je verder nog iets vindt/bedenkt hoor ik het natuurlijk graag
Over het algemeen zijn chlorofyl a en chlorofyl b de meest voorkomende soorten, dat wist ik al, maar ik dacht dat als ik steeds dezelfde soort, en dezelfde portie bonen gebruik, dat dan dezelfde grafiek zou ontstaan. Over die pieken en dalen, ze zitten vooral op een andere hoogte, zie het plaatje
(0 g/L = rood; 5 g/L = blauw; 10 g/L = paars; 15 g/L = oranje; 20 g/L = groen; en er is geen rode lijn te zien omdat hij precies samenvalt met de blauwe)
http://www.filedropper.com/scheikundeallegrafieken
ik vond zelf dat de groene lijn erg lijkt op het absorptiespectrum van chlorofyl a en chlorofyl b
http://commons.wikimedia.org/wiki/File:Chlorophyll_ab_spectra.png
Ik vind je theorie eigenlijk wel heel logisch klinken, maar als je verder nog iets vindt/bedenkt hoor ik het natuurlijk graag
Ik houd je in de gaten...


Ok, het is dus alleen een verschil in hoogte van de pieken. Zo snel gekeken lijken er geen verschillen te zijn in de stoffen.
Heb je ook eiklijnen gemaakt? (Dus een keer door de spectroscoop met alleen het water en de verschillende schone zoutoplossingen)
Maar weet je zeker dat oranje de 15 g/L is, en rood de 0 g/L?
De rode lijn is bij mij trouwens een zwarte lijn...
Heb je ook eiklijnen gemaakt? (Dus een keer door de spectroscoop met alleen het water en de verschillende schone zoutoplossingen)
Maar weet je zeker dat oranje de 15 g/L is, en rood de 0 g/L?
De rode lijn is bij mij trouwens een zwarte lijn...
www.4beta.nl
www.youtube.nl/jweckhardt
---
Als je het niet simpel kunt uitleggen, begrijp je het niet goed genoeg
www.youtube.nl/jweckhardt
---
Als je het niet simpel kunt uitleggen, begrijp je het niet goed genoeg


Die zwarte lijn is een schaduw van de rode lijn, die rode lijn is precies onder de blauwe lijn, en k heb inderdaad ijklijnen gemaakt, maar ik kom er nu achter dat ik echt een hele domme fout heb gemaakt, ik heb uit de verschillende metingen grafieken klakkeloos in één plaatje geplakt, zonder rekening te houden met de schaalverhoudingen van de verschillende metingen, dus dat ga ik nu eerst doen, en dan kijken of het wat logischer is, want de oranje lijn vond ik zelf ook al een beetje vreemd
Ik houd je in de gaten...


Nu wordt in mijn boek gezegd dat het d moet zijn, omdat:quote:Under control conditions, flow through a blood vessel is 100 ml/min with a pressure gradient of 50 mm Hg. What would be the approximate flow through the vessel after increasing the vessel diameter by 50%, assuming the pressure gradient is maintained at 100 mm Hg?
a. 100 ml/min
b. 150 ml/min
c. 300 ml/min
d. 500 ml/min
e. 700 ml/min
Nou ben ik het hier mee eens, maar de druk stijgt toch ook van 50 mm Hg naar 100 mm Hg, en volgens de wet van Poiseuille stijgt de flow als je de drukgradient toe laat nemen. In het antwoord is daar geen rekening mee gehouden. Weet iemand waarom?quote:Blood flow in a vessel is directly proportional to the fourth power of the vessel radius. Increasing vessel diameter by 50% (1.5 times control) would increase blood flow 1.5 to the fourth power x normal blood flow (100 ml/min). Thus blood flow would increase to 100 ml/min * 5,06, or approximately 500 ml/min.


Okee, hier is dan opnieuw de link, maar nu wel rekening gehouden hebbend met de schaalverdelingen
http://www.filedropper.com/allegrafieken
0 g/L = rood; 5 g/L = geel; 10 g/L = roze; 15 g/L = blauw; 20 g/L = lichtgroen
Het resultaat is er alleen niet veel logischer op geworden, vind ik, de pieken zitten nu wel op dezelfde plek, maar ik geloof niet dat hier conclusies uit getrokken kunnen worden...
http://www.filedropper.com/allegrafieken
0 g/L = rood; 5 g/L = geel; 10 g/L = roze; 15 g/L = blauw; 20 g/L = lichtgroen
Het resultaat is er alleen niet veel logischer op geworden, vind ik, de pieken zitten nu wel op dezelfde plek, maar ik geloof niet dat hier conclusies uit getrokken kunnen worden...
Ik houd je in de gaten...


Het is inderdaad niet heel veel logischer geworden.
Een paar mogelijke opties:
De celwanden zijn geen perfecte membramen, en laten dus ook chlorofyl door.
Bij een hypertone oplossing (0 en 5 g/L) zal er veel water, en dus ook veel chlorofyl door het membraam heen gaan.
Bij een isotone oplossing zal er vrijwel niets door het membraam heen gaan.
Maar wat die lichtgroen (20 g/L) nu zo relatief hoog doet...
Weet je zeker dat dit een scheikunde-practicum is? Ergens heb ik het gevoel dat er nog wat biologische factoren mee lijken te spelen (beschadiging van celwanden in te zoute omgeving etc.)
Een paar mogelijke opties:
De celwanden zijn geen perfecte membramen, en laten dus ook chlorofyl door.
Bij een hypertone oplossing (0 en 5 g/L) zal er veel water, en dus ook veel chlorofyl door het membraam heen gaan.
Bij een isotone oplossing zal er vrijwel niets door het membraam heen gaan.
Maar wat die lichtgroen (20 g/L) nu zo relatief hoog doet...
Weet je zeker dat dit een scheikunde-practicum is? Ergens heb ik het gevoel dat er nog wat biologische factoren mee lijken te spelen (beschadiging van celwanden in te zoute omgeving etc.)
www.4beta.nl
www.youtube.nl/jweckhardt
---
Als je het niet simpel kunt uitleggen, begrijp je het niet goed genoeg
www.youtube.nl/jweckhardt
---
Als je het niet simpel kunt uitleggen, begrijp je het niet goed genoeg


Dit is echt een scheikunde experiment, alhoewel ik hem zelf ook eerder bij biologie vind horen, door osmose en chlorofyl en zo, maar dit hoort niet bij de lesstof uit ons boek, het is een PO dat er geheel los van staat, en we moesten het experiment bedenken op basis van een ander experiment, dus ik denk wel dat de biologische factoren mee spelen, dan zou wat jij zegt wel eens kunnen kloppen.
Eigenlijk vind ik alle lijnen wel logisch er uit zien ten opzichte van elkaar, want hoe meer chlorofyl er in het water zit, des te minder wordt er in het groen gedeelte licht geabsorbeerd, want er wordt meer groen licht weerkaatst. Dus dan zou er bij de hypertone oplossingen toch juist geen chlorofyl in het water komen? Of in ieder geval minder dan bij de sterkere oplosingen, want de hypertone oplossingen absorberen meer groen licht, dus bevat het water minder chlorofyl, toch?
Als wat ik zeg klopt, dan betekent het dat er bij de 5e oplossing om de een of andere reden er MINDER chlorofyl in het water is gekomen, dan bij de 4e lijn... En dat is het vreemdst, want door meer zout zou de celwand "meer kapot" moeten gaan, en zou er dus juist meer chlorofyl in het water moeten komen...
Eigenlijk vind ik alle lijnen wel logisch er uit zien ten opzichte van elkaar, want hoe meer chlorofyl er in het water zit, des te minder wordt er in het groen gedeelte licht geabsorbeerd, want er wordt meer groen licht weerkaatst. Dus dan zou er bij de hypertone oplossingen toch juist geen chlorofyl in het water komen? Of in ieder geval minder dan bij de sterkere oplosingen, want de hypertone oplossingen absorberen meer groen licht, dus bevat het water minder chlorofyl, toch?
Als wat ik zeg klopt, dan betekent het dat er bij de 5e oplossing om de een of andere reden er MINDER chlorofyl in het water is gekomen, dan bij de 4e lijn... En dat is het vreemdst, want door meer zout zou de celwand "meer kapot" moeten gaan, en zou er dus juist meer chlorofyl in het water moeten komen...
Ik houd je in de gaten...


Hey iedereen,
tijdens het oefenen van rekenopgaven scheikunde kwam ik bij deze vraag niet uit:
Gegeven butaanzuur / 20,00 mmol en dichtheid p= 0,9577 * 10-3 kg/m3
Bereken hoeveel microliter je nodig hebt ?
Eerst bereken ik de deeltjesmassa van butaanzuur:
C= 4 x 12,01 u
O= 2 x 16,00 u
H= 8 x 1,008 u
-------------------- +
88,104 u => Dus 88,104 g/mol
20,00 mmol = 0,02 mol => 0,02 mol x 88,104 g/mol = 1,76208 gram
Dichtheid: 0,95577 x 10-3 kg/m3
= 0,95577 x 10-3 g/L
0,9577 x 10-3 x 1,76208 g = 0,001687544 L
= 1687,544 microliter
Maar het antwoord klopt niet, dus kan iemand mijn denkwijze/rekenfout opsporen ?
Alvast bedankt
tijdens het oefenen van rekenopgaven scheikunde kwam ik bij deze vraag niet uit:
Gegeven butaanzuur / 20,00 mmol en dichtheid p= 0,9577 * 10-3 kg/m3
Bereken hoeveel microliter je nodig hebt ?
Eerst bereken ik de deeltjesmassa van butaanzuur:
C= 4 x 12,01 u
O= 2 x 16,00 u
H= 8 x 1,008 u
-------------------- +
88,104 u => Dus 88,104 g/mol
20,00 mmol = 0,02 mol => 0,02 mol x 88,104 g/mol = 1,76208 gram
Dichtheid: 0,95577 x 10-3 kg/m3
= 0,95577 x 10-3 g/L
0,9577 x 10-3 x 1,76208 g = 0,001687544 L
= 1687,544 microliter
Maar het antwoord klopt niet, dus kan iemand mijn denkwijze/rekenfout opsporen ?
Alvast bedankt
Als je het moet vragen, zul je het nooit weten.
En als je het weet, hoef je het maar te vragen.
En als je het weet, hoef je het maar te vragen.


massa * dichtheid ?quote:Op zondag 8 april 2012 18:57 schreef Nutkicker22 het volgende:
Hey iedereen,
tijdens het oefenen van rekenopgaven scheikunde kwam ik bij deze vraag niet uit:
Gegeven butaanzuur / 20,00 mmol en dichtheid p= 0,9577 * 10-3 kg/m3
Bereken hoeveel microliter je nodig hebt ?
Eerst bereken ik de deeltjesmassa van butaanzuur:
C= 4 x 12,01 u
O= 2 x 16,00 u
H= 8 x 1,008 u
-------------------- +
88,104 u => Dus 88,104 g/mol
20,00 mmol = 0,02 mol => 0,02 mol x 88,104 g/mol = 1,76208 gram
Dichtheid: 0,95577 x 10-3 kg/m3
= 0,95577 x 10-3 g/L
0,9577 x 10-3 x 1,76208 g = 0,001687544 L
= 1687,544 microliter
Maar het antwoord klopt niet, dus kan iemand mijn denkwijze/rekenfout opsporen ?
Alvast bedankt
kg * kg/m^3 = kg^2/m^3
dus dat klopt hier niet
massa/dichtheid = volume
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]