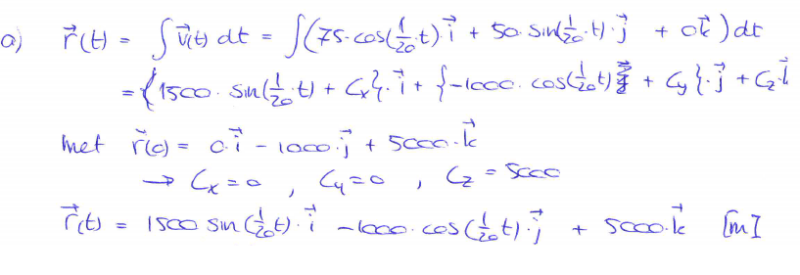SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Kan iemand hierheen kijken?
Laat zien of de volgende lineaire afbeeldingen injectief, surjectief of bijectief is:
f: R3->R2 : (x,y,z) |--> (x-y,2z)
Injectief:
Nee, want voor elke x,y in R, met x=/ 0, en x=y geldt voor z=0
f(x,y,z) = (0,0)
Aangezien x=y=/0, is deze afbeelding dus niet injectief.
Surjectief:
f(1,0,0) = (1,0) =f(v1)
f(0,1,0) = (-1,0)= f(v2)
f(0,0,1)= (0,1) = f(v3)
We zien dus dat L(f(v1),f(v3))= R2. Aangezien voor elke x,y,z in R (x-y,2z) een element uit R2 is, is f dus surjectief.
Laat zien of de volgende lineaire afbeeldingen injectief, surjectief of bijectief is:
f: R3->R2 : (x,y,z) |--> (x-y,2z)
Injectief:
Nee, want voor elke x,y in R, met x=/ 0, en x=y geldt voor z=0
f(x,y,z) = (0,0)
Aangezien x=y=/0, is deze afbeelding dus niet injectief.
Surjectief:
f(1,0,0) = (1,0) =f(v1)
f(0,1,0) = (-1,0)= f(v2)
f(0,0,1)= (0,1) = f(v3)
We zien dus dat L(f(v1),f(v3))= R2. Aangezien voor elke x,y,z in R (x-y,2z) een element uit R2 is, is f dus surjectief.
f(v3) is geen (0,1) maar (0,2).
Je laatste zin snap ik niet (wat is L?). Surjectief toon je aan dat elk element uit R² bereikt kan worden, en dat volgt idd uit lineariteit, f(v1) en f(v3).
Je laatste zin snap ik niet (wat is L?). Surjectief toon je aan dat elk element uit R² bereikt kan worden, en dat volgt idd uit lineariteit, f(v1) en f(v3).
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Klopt, dat was een typefoutje.quote:Op donderdag 13 januari 2011 13:41 schreef GlowMouse het volgende:
f(v3) is geen (0,1) maar (0,2).
Je laatste zin snap ik niet (wat is L?). Surjectief toon je aan dat elk element uit R² bereikt kan worden, en dat volgt idd uit lineariteit, f(v1) en f(v3).
Met L(f(v1),f(v3)) bedoel ik het lineaire opspansel van f(v1),f(v3).
Dit stukje vind ik ook een beetje vaag. Bedoel je met de laatste zin misschien: aangezien f(0,0,0)=(0,0) is de afbeelding niet injectief?quote:
Kan iemand hierheen kijken?
Laat zien of de volgende lineaire afbeeldingen injectief, surjectief of bijectief is:
f: R3->R2 : (x,y,z) |--> (x-y,2z)
Injectief:
Nee, want voor elke x,y in R, met x=/ 0, en x=y geldt voor z=0
f(x,y,z) = (0,0)
Aangezien x=y=/0, is deze afbeelding dus niet injectief.
Ik zou het zo doen:
Injectief betekent f(x)=f(y) => x=y. Het is makkelijk om met tegenspraak te laten zien dat ie niet injectief is; Stel f is injectief. Dan volgt uit f(0,0,1)=f(1,1,1)=(0,2), dat (0,0,1)=(1,1,1) (tegenspraak).
Ik maak gebruik van het gegeven dat als Ker f = 0 dan en alleen dan is f injectief.quote:
[..]
Dit stukje vind ik ook een beetje vaag. x mag ook best nul zijn, want dan is x-y ook nog nul als x=y.
Ik zou het zo doen:
Injectief betekent f(x)=f(y) => x=y. Het is makkelijk om met tegenspraak te laten zien dat ie niet injectief is; Stel f is injectief. Dan volgt uit f(0,0,1)=f(1,1,1)=(0,0,2), dat (0,0,1)=(1,1,1) (tegenspraak).
Bewijs:
Stel alleen f(0)=0
Dan voor f(v)=f(v') , dan f(v-v')=f(0) betekent dat v=v'.
Oftewel de definitie van injectief.
Ah ja, zo kan het ookquote:
[..]
Ik maak gebruik van het gegeven dat als Ker f = 0 dan en alleen dan is f injectief.
Bewijs:
Stel alleen f(0)=0
Dan voor f(v)=f(v') , dan f(v-v')=f(0) betekent dat v=v'.
Oftewel de definitie van injectief.
Het klinkt stom, maar kan iemand me een voorbeeld geven van een niet surjectieve afbeelding?quote:
Op En belangrijker, hoe bewijs je dat?
f: R-> R , f(x)=x²quote:
[..]
Het klinkt stom, maar kan iemand me een voorbeeld geven van een niet surjectieve afbeelding?
En belangrijker, hoe bewijs je dat?
f is niet surjectief omdat f(x)=/ -1 voor alle x in het domein van f (een kwadraat is altijd niet-negatief). Dus -1 ligt wel in het codomein maar wordt niet bereikt => niet surjectief.
Maar het codomein wordt dus niet beschreven door, in dit geval, x2, maar is gewoon R ?quote:Op donderdag 13 januari 2011 14:22 schreef BasementDweller het volgende:
[..]
f: R-> R , f(x)=x²
f is niet surjectief omdat f(x)=/ -1 voor alle x (een kwadraat is altijd niet-negatief). Dus -1 ligt wel in het codomein maar wordt niet bereikt => niet surjectief.
Ja. Het codomein mag je eigenlijk zelf kiezen, zo lang het bereik van de functie er maar een deelverzameling van is.quote:
[..]
Maar het codomein wordt dus niet beschreven door, in dit geval, x2, maar is gewoon R ?
Als je dezelfde functie had genomen met als codomein: alle niet-negatieve reële getallen, dan was ie wel surjectief geweest.
Ik zie net je edit:quote:
[..]
Ja. Het codomein mag je eigenlijk zelf kiezen, zo lang het bereik van de functie er maar een deelverzameling van is.
Als je dezelfde functie had genomen met als codomein: alle niet-negatieve reële getallen, dan was ie wel surjectief geweest.
Alles mbt surjectieviteit word meteen een stuk duidelijker.
Bedankt!
N=natuurlijke getallen? Dan heb je je functie niet goed gedefiniëerd, want dan heeft f(1/2) geen uitkomst, want (1/2)^2 = 1/4 (niet in N).quote:
[..]
Dus als het codomein N, domein gewoon R laten, in dit geval was geweest, was de functie wél surjectief?
Klopt, ik merkte het al toen ik op invoeren drukte.quote:
[..]
N=natuurlijke getallen? Dan heb je je functie niet goed gedefiniëerd, want dan heeft f(1/2) geen uitkomst, want (1/2)^2 = 1/4 (niet in N).
Ik zit met iets.
0,05 is hetzelfde als 20-1
0,05t is hetzelfde als 20-1t
Nu gaan we integraal nemen:
f 0,05t = 0,025t2 toch?
f 20-1t = 20
Ben ik nou gek v_v?
0,05 is hetzelfde als 20-1
0,05t is hetzelfde als 20-1t
Nu gaan we integraal nemen:
f 0,05t = 0,025t2 toch?
f 20-1t = 20
Ben ik nou gek v_v?
Blues ain't nothing but a good man feeling bad...
Bedoel je met 'f' een primitieve? Een primitieve van 20^(-1)*t is bijv. 20^(-1)*t^2/2, in ieder geval niet 20.quote:
Ik zit met iets.
0,05 is hetzelfde als 20-1
0,05t is hetzelfde als 20-1t
Nu gaan we integraal nemen:
f 0,05t = 0,025t2 toch?
f 20-1t = 20
Ben ik nou gek v_v?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Moet een integraal teken voorstellen.
f ( 0,05t) dt= 0,025t2
f ( 20-1t) dt = 20
f ( 0,05t) dt= 0,025t2
f ( 20-1t) dt = 20
Blues ain't nothing but a good man feeling bad...
v(t) = 75cos(0,05t)
Ik wil deze snelheids vector omzetten naar een positie vector, dus v integreren naar s.
Dus 75cos(0,05t) als je dat integreert word het 75sin(0,05t) MAAL de integraal van 0,05t. Product regels is dat geloof ik he. En toen zag ik dat de uitkomst daarvan 20 is.
Ik wil deze snelheids vector omzetten naar een positie vector, dus v integreren naar s.
Dus 75cos(0,05t) als je dat integreert word het 75sin(0,05t) MAAL de integraal van 0,05t. Product regels is dat geloof ik he. En toen zag ik dat de uitkomst daarvan 20 is.
Blues ain't nothing but a good man feeling bad...
Zoals gezegd, die tweede klopt niet.quote:
Moet een integraal teken voorstellen.
f ( 0,05t) dt= 0,025t2
f ( 20-1t) dt = 20
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Hier gaat het om:
Zoals je ziet staat er 1500. Dat betekent dus dat 75 met 20 is vermenigvuldigd. Waar komt die 20 dan vandaan?
Zoals je ziet staat er 1500. Dat betekent dus dat 75 met 20 is vermenigvuldigd. Waar komt die 20 dan vandaan?
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Blues ain't nothing but a good man feeling bad...
Nee, de integraal van v(s) = 75*cos(0.05*s) voor s van 0 tot t wordt (75/0.05)*sin(0.05t).quote:
v(t) = 75cos(0,05t)
Ik wil deze snelheids vector omzetten naar een positie vector, dus v integreren naar s.
Dus 75cos(0,05t) als je dat integreert word het 75sin(0,05t) MAAL de integraal van 0,05t. Product regels is dat geloof ik he. En toen zag ik dat de uitkomst daarvan 20 is.
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
De kettingregel, differentieren van (75/0.05)*sin(0.05t) geeft (75/0.05)*cos(0.05*t)*0.05 = 75*cos(0.05*t).quote:
Wat voor een rekenregel is dit dan?
heeft de hoop dat het allemaal stiekum toch nog goed komt...
Fotoboek
Fotoboek
Moeilijke integralen hebben vaak een uitkomst die simpel te differentieren valt.quote:
Wat voor een rekenregel is dit dan?
Gebruik dat dan om te controleren of je ook echt de goede integraal hebt.
[ Bericht 0% gewijzigd door Siddartha op 13-01-2011 18:01:43 ]
Waar baseer je dat op? Ik ken genoeg 'eenvoudige' functies waarvan een primitieve niet in elementaire functies is uit te drukken, maar daaruit volgt niet dat omgekeerd 'moeilijke' functies eenvoudig te primitiveren zouden zijn.quote:
[..]
Moeilijke integralen hebben vaak een uitkomst die simpel te integreren valt.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |