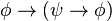[Bèta wiskunde] Huiswerk- en vragentopic

quote:

Op dinsdag 2 maart 2010 15:40 schreef Siddartha het volgende:

[..]

In het boek staat gewoon 'het vlakdeel', wat in dit geval gelijk is aan het volume (toch?).

Nee, want een vlakdeel heeft geen volume. En bij een omwentelingslichaam kan het ook nog zijn dat wordt gevraagd de oppervlakte van dat omwentelingslichaam te berekenen. In de opgave moet duidelijk staan wat de bedoeling is.

quote:

Uitkomst had ik 1/12Pi^2 + 1/8Pi Wortel3
(als primitive functie had ik F(x) = 1/2x -1/8sin4x , invullen voor b=1/3pi en a = 1/6 pi, etc geeft de inhoud. Dat keer Pi en ik heb de uitkomst.)

Dit is correct.

quote:

Maar ik vind het vreemd dat je de originele functie moet kwadrateren en niet de uitkomsten van de integrale functie.

Snijd het omwentelingslichaam in gedachten eens in n hele dunne plakjes met een dikte Δx, waarbij het snijvlak loodrecht op de as van de rotatie staat. Elk van die dunne plakjes kun je bij benadering als een cilinder met straal f(x_k) en lengte Δx beschouwen. Het volume van één zo'n cilinder is dan π∙{f(x_k)}²∙Δx. Het volume van al die plakjes (met k = 1,2 ... n) moet je sommeren om een benadering te krijgen van het volume van het omwentelingslichaam. Deze benadering wordt beter naarmate je de plakjes dunner maakt. Zo krijg je de limiet van wat ze wel een Riemann som noemen, en deze limiet is de integraal die je hebt uitgerekend.

Wat jij wilde is de oppervlakte van het vlakdeel kwadrateren, maar daarmee bereken je geen inhoud (waarom niet?). Probeer het maar eens met wat eenvoudige figuren als een cirkel of een vierkant die je om hun symmetrie-as roteert, dan zie je dat jouw idee over het volume van een omwentelingslichaam niet klopt.

[ Bericht 0% gewijzigd door Riparius op 02-03-2010 18:57:45 ]

Te stom voor woorden

Plaatsvervangend probleempje voor wie het leuk vind om over na te denken.
Construeer vierkant met alleen een passer en een lineaal.
(dus GEEN geo ofzo).

[ Bericht 77% gewijzigd door Borizzz op 02-03-2010 21:19:07 ]

quote:

Op dinsdag 2 maart 2010 21:12 schreef GlowMouse het volgende:
Reken die kansen eens afzonderlijk voor mij uit dan

GGB: 6/14 * 5/13 * 8/12 =10/91

GBG: 6/14 * 8/13 * 5/12 =10/91

BGG: 8/14 * 6/13 * 5/12 = 10/91

Samen 30/91ong 0.3296
Oke laat maar, kleine misvatting

Maar ik vind het didactisch niet echt verantwoord om het zo kort neer te zetten.
Beter is het om het geheel uit te werken en het te laten zien.

Kan iemand mij vlug uitleggen hoe ik de Y kan of moet vrijmaken? Aub beginnen met iets heel elementairs.

quote:

Op dinsdag 2 maart 2010 16:39 schreef Riparius het volgende:

[..]
Snijd het omwentelingslichaam in gedachten eens in n hele dunne plakjes met een dikte Δx, waarbij het snijvlak loodrecht op de as van de rotatie staat. Elk van die dunne plakjes kun je bij benadering als een cilinder met straal f(x_k) en lengte Δx beschouwen. Het volume van één zo'n cilinder is dan π∙{f(x_k)}²∙Δx. Het volume van al die plakjes (met k = 1,2 ... n) moet je sommeren om een benadering te krijgen van het volume van het omwentelingslichaam. Deze benadering wordt beter naarmate je de plakjes dunner maakt. Zo krijg je de limiet van wat ze wel een Riemann som noemen, en deze limiet is de integraal die je hebt uitgerekend.

Wat jij wilde is de oppervlakte van het vlakdeel kwadrateren, maar daarmee bereken je geen inhoud (waarom niet?). Probeer het maar eens met wat eenvoudige figuren als een cirkel of een vierkant die je om hun symmetrie-as roteert, dan zie je dat jouw idee over het volume van een omwentelingslichaam niet klopt.

Dus een integraal is de somfunctie van alle 'y' op gebied delta x (waar x zo klein mogelijk is) en is dus voor elke delta x eigenlijk (een benadering van) de straal?
Hmm, wat ik dus deed was puur de oppervlakte kwadrateren, terwijl oppervlakte niet gelijk is aan straal. Wat ik deed was de stralen/lijnen onder het gegeven gebied uitrekenen, bij elkaar optellen en dan kwadrateren. Door de formule van de integraal te kwadrateren, kwadrateer ik elke straal en ( x Pi) krijg ik wel de inhoud.
Klopt dit een beetje?

quote:

Op dinsdag 2 maart 2010 23:40 schreef Siddartha het volgende:

[..]

Dus een integraal is de somfunctie van alle 'y' op gebied delta x (waar x zo klein mogelijk is) en is dus voor elke delta x eigenlijk (een benadering van) de straal?
Hmm, wat ik dus deed was puur de oppervlakte kwadrateren, terwijl oppervlakte niet gelijk is aan straal. Wat ik deed was de stralen/lijnen onder het gegeven gebied uitrekenen, bij elkaar optellen en dan kwadrateren. Door de formule van de integraal te kwadrateren, kwadrateer ik elke straal en ( x Pi) krijg ik wel de inhoud.
Klopt dit een beetje?

Ik volg het niet helemaal waarom je de stappen neemt die je neemt, maar volgens mij klopt het niet.

Een voorbeeld:
De straal van het cilindertje is de functiewaarde en de "hoogte" van de cilinder is de dx. Je kan het zien als een worst die je in infinitesimaal dunne plakjes snijdt. Als je de volumes van de kleine plakjes bij elkaar optelt heb je het formule van de hele worst. Een worst die in dikte varieert kan je zien als een niet-constante functie. Stel dat je worst wel kaarsrecht is met constante straal f(x)=c en lengte L. Dan kun je de inhoud uitrekenen met de "standaardformule" voor een cilinder: pi × c² × L (dat is dus gewoon de "oppervlakte maal hoogte". Je kan ook de volgende integraal uitrekenen:

Voor een gewone cilinder is dit eigenlijk overbodig werk, maar het geeft je misschien wel een idee dat het voor niet-constante formules ook de inhoud geeft.

Misschien is het wel een leuke oefening om mbv een omwentelingslichaam de inhoud van een kegel met hoogte L te bepalen . Je zou een kegel kunnen kiezen met als tophoek 90 graden. Dan kan je de functie f(x)=x gebruiken. Welke integraal bereken je dan?

[ Bericht 2% gewijzigd door motorbloempje op 01-09-2013 21:40:28 ]

quote:

Op woensdag 3 maart 2010 00:29 schreef BasementDweller het volgende:

[..]

Ik volg het niet helemaal waarom je de stappen neemt die je neemt, maar volgens mij klopt het niet.

Een voorbeeld:
De straal van het cilindertje is de functiewaarde en de "hoogte" van de cilinder is de dx. Je kan het zien als een worst die je in infinitesimaal dunne plakjes snijdt. Als je de volumes van de kleine plakjes bij elkaar optelt heb je het formule van de hele worst. Een worst die in dikte varieert kan je zien als een niet-constante functie. Stel dat je worst wel kaarsrecht is met constante straal f(x)=c en lengte L. Dan kun je de inhoud uitrekenen met de "standaardformule" voor een cilinder: pi × c² × L (dat is dus gewoon de "oppervlakte maal hoogte". Je kan ook de volgende integraal uitrekenen:
[ afbeelding ]
Voor een gewone cilinder is dit eigenlijk overbodig werk, maar het geeft je misschien wel een idee dat het voor niet-constante formules ook de inhoud geeft.

Misschien is het wel een leuke oefening om mbv een omwentelingslichaam de inhoud van een kegel met hoogte L te bepalen . Je zou een kegel kunnen kiezen met als tophoek 90 graden. Dan kan je de functie f(x)=x gebruiken. Welke integraal bereken je dan?

Ik had in een opgave de uitkomst van de integraal gekwadrateerd en vroeg me af waarom je de hele formule moest kwadrateren. Maar dat is dus omdat de integraal een verzameling is van stralen (of benaderingen ervan) voor elk stapje delta x binnen het aangegeven gebied?

Hmm, een kegel. De f(x) lijn is in dit geval de schuine zijde, de x-lijn de hoogte(L) en x=b is de straal. Als ik f(x) primitiveer en voor 2 getallen invul (waarvan a = 0), krijg ik de oppervlakte onder de lijn. Zonder de primitive had ik gewoon uitgerekent: Pi x straal^2 x L x 1/3
Maar omdat F(x) = 1/2x^2 voor (b=x en a=0) al de oppervlakte geeft, hoef ik toch alleen maar:
Pi x F(x)^2 uit te rekenen?

quote:

Op woensdag 3 maart 2010 08:19 schreef Siddartha het volgende:

[..]

Ik had in een opgave de uitkomst van de integraal gekwadrateerd en vroeg me af waarom je de hele formule moest kwadrateren. Maar dat is dus omdat de integraal een verzameling is van stralen (of benaderingen ervan) voor elk stapje delta x binnen het aangegeven gebied?

Hmm, een kegel. De f(x) lijn is in dit geval de schuine zijde, de x-lijn de hoogte(L) en x=b is de straal. Als ik f(x) primitiveer en voor 2 getallen invul (waarvan a = 0), krijg ik de oppervlakte onder de lijn. Zonder de primitive had ik gewoon uitgerekent: Pi x straal^2 x L x 1/3
Maar omdat F(x) = 1/2x^2 voor (b=x en a=0) al de oppervlakte geeft, hoef ik toch alleen maar:
Pi x F(x)^2 uit te rekenen?

Nee, je vervalt weer in dezelfde denkfout door de primitieve te kwadrateren, en daarmee in feite de oppervlakte van het vlakdeel omder de curve te kwadrateren.

quote:

Op woensdag 3 maart 2010 08:44 schreef Riparius het volgende:

[..]

Nee, je vervalt weer in dezelfde denkfout door de primitieve te kwadrateren, en daarmee in feite de oppervlakte van het vlakdeel omder de curve te kwadrateren.

In de laatste regel bedoel ik F(x) als gehele functie te kwadrateren, dus
F(x) = 1/2x^2
F(x)^2 = 1/4x^4 (En daarvoor invullen, x Pi geeft het volume, toch?)

quote:

Op woensdag 3 maart 2010 09:05 schreef Siddartha het volgende:

[..]

In de laatste regel bedoel ik F(x) als gehele functie te kwadrateren, dus
F(x) = 1/2x^2
F(x)^2 = 1/4x^4 (En daarvoor invullen, x Pi geeft het volume, toch?)

Ik begrijp wat je bedoelt, maar het is gewoon fout. Het volume van een omwentelingslichaam verkregen door de curve van y = f(x) tussen x=a en x= b rond de x-as te wentelen wordt gegeven door:

(1) π∙∫_a^b (f(x))²dx

Maar wat jij schijnt te denken is dat dit hetzelfde is als:

(2) π∙[∫_a^b f(x)dx]²

Maar (2) is niet hetzelfde als (1), en bovendien kan (2) onmogelijk het volume van het omwentelingslichaam voorstellen. Zie je ook waarom?

Hallo,

Ik heb wat vragen over ontbinden in factoren:

1. Ik begrijp deze stappen niet:



2. Ik moet de determinant van een matrix bepalen. Ik kom op de hieronderstaande waarde uit:
( de vergelijking moet als uitkomst 0 hebben).




Als antwoord is alleen het eindantwoord gegeven: a = 0 a = 1 of a = 2.
Ik kom hier niet op uit heb ik iets fout gedaan of zien jullie deze antwoorden zo?

Alvast bedankt

[ Bericht % gewijzigd door motorbloempje op 01-09-2013 21:40:33 ]

quote:

Op woensdag 3 maart 2010 13:35 schreef Matr het volgende:
Hallo,

Ik heb wat vragen over ontbinden in factoren:

1. Ik begrijp deze stappen niet:

[ afbeelding ]

2. Ik moet de determinant van een matrix bepalen. Ik kom op de hieronderstaande waarde uit:
( de vergelijking moet als uitkomst 0 hebben).

[ afbeelding ]


Als antwoord is alleen het eindantwoord gegeven: a = 0 a = 1 of a = 2.
Ik kom hier niet op uit heb ik iets fout gedaan of zien jullie deze antwoorden zo?

Alvast bedankt

1. Een derdegraads polynoom is wat lastig te ontbinden in factoren tenzij je tenminste één van de nulpunten zo al ziet (of echt een kubische vergelijking wilt gaan oplossen), maar in dit geval is het betrekkelijk eenvoudig. Het product van de wortels van a³ - 3a + 2 = 0 is -2, dus ligt het voor de hand plus of min 1 en plus of min 2 te proberen, en dan kom je er snel achter dat a = 1 en a = -2 voldoen. Door het uitvoeren van een polynoomstaartdeling vind je dan (a³ - 3a + 2)/(a + 2) = a² - 2a + 1, en dus a³ - 3a + 2 = (a + 2)(a² - 2a + 1). Verder is a² - 2a + 1 = (a - 1)², maar dat is gewoon een kwestie van het merkwaardig product (a - b)² = a² -2ab + b² gebruiken.

2. Hier ben je kennelijk haakjes vergeten. Als je hebt (a - 1)(a² - 2a) = 0 dan kun je uit de tweede factor van dit product nog een factor a buiten haakjes halen en krijg je dus a(a - 1)(a - 2) = 0, waaruit volgt a = 0 of a = 1 of a = 2.

Tnx zal het binnenkort even narekenen

quote:

Op woensdag 3 maart 2010 09:18 schreef Riparius het volgende:

[..]

Ik begrijp wat je bedoelt, maar het is gewoon fout. Het volume van een omwentelingslichaam verkregen door de curve van y = f(x) tussen x=a en x= b rond de x-as te wentelen wordt gegeven door:

(1) π∙∫_a^b (f(x))²dx

Maar wat jij schijnt te denken is dat dit hetzelfde is als:

(2) π∙[∫_a^b f(x)dx]²

Maar (2) is niet hetzelfde als (1), en bovendien kan (2) onmogelijk het volume van het omwentelingslichaam voorstellen. Zie je ook waarom?

Hmm, wat ik deed was dus weer dezelfde fout: De oppervlakte kwadrateren.
Door f(x) te kwadrateren, kwadrateer je alleen de straal voor elke x, en met integreren tel je dan alle gekwadrateerde stralen in een gebied(=lengte) bij elkaar op. En dus heb je de straal^2 x lengte zo berekent.( Dan volgt vanzelf keer Pi)
Terwijl je door F(x) te kwadrateren, tel je alle stralen bij elkaar op in een gebied en dat kwadrateer je. Wat dus fout is.
Ik denk dat ik het nu snap!

quote:

Op woensdag 3 maart 2010 15:41 schreef Siddartha het volgende:

[..]

Hmm, wat ik deed was dus weer dezelfde fout: De oppervlakte kwadrateren.
Door f(x) te kwadrateren, kwadrateer je alleen de straal voor elke x, en met integreren tel je dan alle gekwadrateerde stralen in een gebied(=lengte) bij elkaar op. En dus heb je de straal^2 x lengte zo berekend.( Dan volgt vanzelf keer Pi)
Terwijl je door F(x) te kwadrateren, tel je alle stralen bij elkaar op in een gebied en dat kwadrateer je. Wat dus fout is.
Ik denk dat ik het nu snap!

Je kunt het beste denken aan het verdelen van een omwentelingslichaam in hele dunne plakjes die elk bij benadering een cilinder zijn. Door de volumina van die cilinders bij elkaar op te tellen krijg je een benadering voor het volume van het omwentelingslichaam die beter wordt naarmate de plakjes dunner worden. Een integraal is in principe te definiëren als de limiet van een dergelijke Riemann som. Dat suggereert het integraalteken ook. De ∫ is oorspronkelijk een langgerekte s van summa. Probeer om het principe beter te begrijpen eens of je ook een formule kunt opstellen voor de manteloppervlakte van een omwentelingslichaam (hint: stel eerst een formule op voor de lengte van de curve van y = f(x) tussen x=a en x=b).

quote:

Op woensdag 3 maart 2010 15:56 schreef Riparius het volgende:

[..]
Probeer om het principe beter te begrijpen eens of je ook een formule kunt opstellen voor de manteloppervlakte van een omwentelingslichaam (hint: stel eerst een formule op voor de lengte van de curve van y = f(x) tussen x=a en x=b).

Nou, de lengte is y voor f(delta x) maal 2 omdat je met y alleen maar de straal van het midden naar de 'cirkel' hebt, terwijl je aan de andere kant nog eens die lengte hebt.
dus lengte is 2y: 2f(x)
Omtrek van een figuur is Pi x lengte.
Om de lengte van elke delta x bij elkaar op te tellen kan ik de integraal gebruiken. Door (2f(x)) te primitiveren tel ik al die lengtes bij elkaar op en door dan met Pi te vermenigvuldigen krijg ik de omtrek/mantel. Toch?

quote:

Op woensdag 3 maart 2010 16:23 schreef Siddartha het volgende:

[..]

Nou, de lengte is y voor f(delta x) maal 2 omdat je met y alleen maar de straal van het midden naar de 'cirkel' hebt, terwijl je aan de andere kant nog eens die lengte hebt.
dus lengte is 2y: 2f(x)
Omtrek van een figuur is Pi x lengte.
Om de lengte van elke delta x bij elkaar op te tellen kan ik de integraal gebruiken. Door (2f(x)) te primitiveren tel ik al die lengtes bij elkaar op en door dan met Pi te vermenigvuldigen krijg ik de omtrek/mantel. Toch?

Nee, dat gaat niet goed. Eerst de booglengte s van de curve van y = f(x) tussen x=a en x=b. Die wordt gegeven door:

(1) s = ∫_a^b √(1 + (f'(x))²)dx

Voor de afleiding van deze formule moet je hier maar even kijken.

Nu de manteloppervlakte. Hierbij neem ik aan dat f(x) op het interval [a,b] niet negatief wordt. Verdeel het omwentelingslichaam weer in heel dunne plakjes met een dikte Δx, dan kun je de manteloppervlakte van één zo'n plakje (ring) benaderen door de booglengte van de curve van y = f(x) over het betreffende interval te vermenigvuldigen met de omtrek 2πr van zo'n ring. Dit geeft als benadering voor de manteloppervlakte van één zo'n ring

2π∙f(x_k)√(1 + (f'(x_k))²)Δx,

waarbij x_k een waarde van x is op het betreffende intervalletje. Om de manteloppervlakte van x=a tot x=b te benaderen moet je al deze stukjes (met k = 1 ... n) optellen, waarbij de benadering weer beter wordt naarmate we de dikte Δx van de plakjes tot nul laten naderen. Voor de manteloppervlakte A van het omwentelingslichaam dat ontstaat door de curve van y = f(x) tusen x=a en x=b om de x-as te wentelen vinden we zo:

(2) A = 2π∙∫_a^b f(x)∙√(1 + (f'(x))²)dx

Probeer eens of je nu formules voor de inhoud en de oppervlakte van een bol met straal r kunt afleiden. Neem f(x) = √(r² - x²) (r > 0). De grafiek hiervan is een halve cirkel met als middelpunt de oorsprong en als straal r, zodat bij wenteling om de x-as een bol met straal r ontstaat.

quote:

Op woensdag 3 maart 2010 17:14 schreef Riparius het volgende:

[..]

Wat ik dus deed gaf niet de oppervlakte van een willekeurig figuur (met f(x) ongedifineerd)?
Ik heb gewoon de formule gepakt van de omtrek van een cirkel (dat gebeurt er namelijk ook op delta x)
2Pi r = Pi maal lengte. En de rest staat in mijn vorige post.

Ik snap niet goed waarvoor ik een booglengte nodig heb?
Waarom moet je nu niet als eerste stap f(x) keer 2 doen? Dan heb je namelijk de 2 x straal op vlakdeel delta x, waarna je kan gaan integreren (en uiteindelijk nog keer Pi).

quote:

Op woensdag 3 maart 2010 17:41 schreef Siddartha het volgende:

[..]

Wat ik dus deed gaf niet de oppervlakte van een willekeurig figuur (met f(x) ongedefineerd)?

Nee.

quote:

Ik heb gewoon de formule gepakt van de omtrek van een cirkel (dat gebeurt er namelijk ook op delta x)
2Pi r = Pi maal lengte. En de rest staat in mijn vorige post.

Nee, om de lengte van één zo'n dunne ring te bepalen moet je de omtrek 2πr = 2πf(x_k) vermenigvuldigen met de breedte van de ring, en die breedte is gelijk aan de booglengte van de curve y = f(x) over dat intervalletje. De breedte van de ring is niet Δx, dat zou alleen zo zijn als de curve horizontaal loopt (en dus f'(x) = 0).

quote:

Ik snap niet goed waarvoor ik een booglengte nodig heb?

Omdat de breedte van elke ring afhangt van de steilheid van de curve op het betreffende intervalletje.

quote:

Waarom moet je nu niet als eerste stap f(x) keer 2 doen? Dan heb je namelijk de 2 x straal op vlakdeel delta x, waarna je kan gaan integreren (en uiteindelijk nog keer Pi).

Op jouw manier bereken je gewoon de oppervlakte van het vlakdeel onder de curve vermenigvuldigd met 2π. Dan krijg je niet de manteloppervlakte van het omwentelingslichaam. Probeer het maar eens met een halve cirkel als curve.

quote:

Op woensdag 3 maart 2010 18:09 schreef Riparius het volgende:

[..]

Nee.
[..]

Nee, om de lengte van één zo'n dunne ring te bepalen moet je de omtrek 2πr = 2πf(x_k) vermenigvuldigen met de breedte van de ring, en die breedte is gelijk aan de booglengte van de curve y = f(x) over dat intervalletje. De breedte van de ring is niet Δx, dat zou alleen zo zijn als de curve horizontaal loopt (en dus f'(x) = 0).
[..]

Omdat de breedte van elke ring afhangt van de steilheid van de curve op het betreffende intervalletje.
[..]

Op jouw manier bereken je gewoon de oppervlakte van het vlakdeel onder de curve vermenigvuldigd met 2π. Dan krijg je niet de manteloppervlakte van het omwentelingslichaam. Probeer het maar eens met een halve cirkel als curve.

Kun je even specificeren wat je me wilt laten doen?
Dus, wat voor figuur en wat ik moet berekenen ( oppervlakte/omtrek/beide)?
En ik neem aan dat lengte is de x-as en y geeft de breedte? (die heb ik in eerdere berichten een paar keer door elkaar gebruikt.)

Trouwens, heel erg bedankt hiervoor. Dit zal meer voor mijn inzicht doen dan puur wat sommetjes maken.

quote:

Op woensdag 3 maart 2010 18:17 schreef Siddartha het volgende:

[..]

Kun je even specificeren wat je me wilt laten doen?
Dus, wat voor figuur en wat ik moet berekenen ( oppervlakte/omtrek/beide)?
En ik neem aan dat lengte is de x-as en y geeft de breedte? (die heb ik in eerdere berichten een paar keer door elkaar gebruikt.)

Trouwens, heel erg bedankt hiervoor. Dit zal meer voor mijn inzicht doen dan puur wat sommetjes maken.

Probeer gewoon eens de oppervlakte en het volume te berekenen van een bol met straal r door een halve cirkel met straal r om de x-as te laten wentelen, zoals ik hierboven al had voorgesteld. Begin maar met het volume, dat is het eenvoudigst.

quote:

Op woensdag 3 maart 2010 18:26 schreef Riparius het volgende:

[..]

Probeer gewoon eens de oppervlakte en het volume te berekenen van een bol met straal r door een halve cirkel met straal r om de x-as te laten wentelen, zoals ik hierboven al had voorgesteld. Begin maar met het volume, dat is het eenvoudigst.

En als je eenmaal het volume hebt is de oppervlakte ook nog maar één stap(je)

quote:

Op woensdag 3 maart 2010 18:26 schreef Riparius het volgende:

[..]

Probeer gewoon eens de oppervlakte en het volume te berekenen van een bol met straal r door een halve cirkel met straal r om de x-as te laten wentelen, zoals ik hierboven al had voorgesteld. Begin maar met het volume, dat is het eenvoudigst.

Volume is:
Eerst de gewone formule: f(x) = Wortel(r^2 - x^2)
Dat kwadrateren, dan primitiveren geeft als volume:
V = Pi x [(r^2)x - 1/3x^3]a,b met a=-r en b=r