Een boer heeft een cirkelvormig weiland. aan de rand van dat weiland staat een paaltje. aan dat paaltje zit een touw vast waar weer een geit aan zit. Het touw is precies zolang dat de geit precies bij de helft van het totale oppervlakte van het weiland kan. Hoe lang is het touw? Hierbij is dus niet eens een straal van het weiland gegeven.
Ik ben benieuwd of iemand van jullie hier een tip over kan geven.
Alvast bedankt. Yannick
Zonder enig getal kun je er toch echt niet meer mee.Het enige wat je met zekerheid kunt zeggen is dat het touw = straal van het weiland.
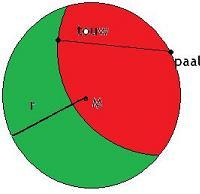
Hierin is het rode en groene deel bij elkaar het weiland, en het rode deel het deel waarin de geit kan grazen. Nu wordt gevraagd naar de lengte van het touw wanneer het groene deel en het rode deel qua oppervlakte gelijk zijn.
dus eerst de totale oppervlak: pi*straal in kwadraat dat deel je door twee dus
pi*r(kwadraat)
------------------
2
en van daar uit moet je dan gaan zoeken hoe je de opp kunt berekenen aan rand van cirkel etc
succes met je huiswerk TS, met dat in ogenschouw genomen is het toch geen moeilijke vraag?
quote:Weet ik, ik ken je namelijk.Op woensdag 2 december 2009 21:41 schreef Yannick3211 het volgende:
je bent wel grappig:p heel toevallig had ik een volle 10 voor mijn examen,, 80 van de 80 punten..
[ Bericht 76% gewijzigd door GlowMouse op 02-12-2009 21:55:21 (NEE GEEN COLA GEVEN) ]
quote:Dat is een andere manier van formuleren, ik dacht dat het schaap precies bij de helft moest komen xD als in de middellijn kunnen bereiken.
[ afbeelding ]
Hierin is het rode en groene deel bij elkaar het weiland, en het rode deel het deel waarin de geit kan grazen. Nu wordt gevraagd naar de lengte van het touw wanneer het groene deel en het rode deel qua oppervlakte gelijk zijn.
quote:Zonder kan ook: http://mathforum.org/library/drmath/view/54871.html of zie http://mathpages.com/home/kmath074/kmath074.htm, maar een exacte oplossing krijg je niet.
Het punt van die site, die ik ook allang gevonden had, is dat het richting de integraalrekening gaat, en dat krijgen wij pas eind dit jaar, dus zou dat niet in de som gebruikt hoeven te worden.
quote:Op woensdag 2 december 2009 21:08 schreef Yannick3211 het volgende:
Hallo, ik ben student op HBO lerarenopleiding wiskunde, en nou wordt de vraag gesteld:
Een boer heeft een cirkelvormig weiland. aan de rand van dat weiland staat een paaltje. aan dat paaltje zit een touw vast waar weer een geit aan zit. Het touw is precies zolang dat de geit precies bij de helft van het totale oppervlakte van het weiland kan. Hoe lang is het touw? Hierbij is dus niet eens een straal van het weiland gegeven.
Ik ben benieuwd of iemand van jullie hier een tip over kan geven.
Alvast bedankt. Yannick
quote:Ja dag, Die straal is nu net wat je moet berekenen. Als de straal gegeven was zou er geen vraag zijn.Op woensdag 2 december 2009 21:10 schreef znarch het volgende:
Precies de straal van het weiland ?
quote:Lees de vraag nog eens goed door.Op woensdag 2 december 2009 21:14 schreef znarch het volgende:
Begint met straal =1 ? Als de straal van het weiland 100 is, is het touw ook 100. Maar maar aangezien er verder niets gegeven is blijft dat gissen.
Het enige wat je met zekerheid kunt zeggen is dat het touw = straal van het weiland.
quote:De vraag van TS was duidelijk. Het ging om de helft van het oppervlak.Op woensdag 2 december 2009 22:06 schreef znarch het volgende:
[..]
Dat is een andere manier van formuleren, ik dacht dat het schaap precies bij de helft moest komen xD als in de middellijn kunnen bereiken.
edit:
Oeps, ik ben spuit11. Het is alweer 5 december.
quote:Alleen geldt dat -1 ≤ cos(x) ≤ 1, dus dat cos(x) - x een oplossing geeft met x = 1,15 lijkt me sterk.
Zo houd je op een gegeven moment een vergelijking met alleen maar "T"tjes, en het valt op mijn niveau nog niet algebraisch op te lossen, je krijgt dit probleem: cos(x) - x = 0. maar goed, dan doe ik het dus met de GR, en dan komt er ongeveer 1,15 uit.
quote:Op dinsdag 15 december 2009 14:55 schreef Yannick3211 het volgende:
...dan doe ik het dus met de GR...
BOOGCOS(1-T^2*(1-COS(2*BOOGCOS(T/2))))/2-SIN((BOOGCOS(1-T^2*(1-COS(2*BOOGCOS(T/2)))))/2)+BOOGCOS(T/2)*T^2= pi/2
neem eens bijvoorbeeld -10. dan krijg je dus een waarde tussen -1 en 1, en daar tel je nog 10 bij op, dus de uitkomst ligt tussen 9 en 11. Maar dat terzijde.
quote:Eh, je zei cos(x) - x = 0. Niet cos(x) - x = y.
En zelfs met cos(x) - x kan ik zo een voorbeeld geven waarbij de uitkomst boven de 1 ligt.
neem eens bijvoorbeeld -10. dan krijg je dus een waarde tussen -1 en 1, en daar tel je nog 10 bij op, dus de uitkomst ligt tussen 9 en 11. Maar dat terzijde.