SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Hallo, ik ben student op HBO lerarenopleiding wiskunde, en nou wordt de vraag gesteld:
Een boer heeft een cirkelvormig weiland. aan de rand van dat weiland staat een paaltje. aan dat paaltje zit een touw vast waar weer een geit aan zit. Het touw is precies zolang dat de geit precies bij de helft van het totale oppervlakte van het weiland kan. Hoe lang is het touw? Hierbij is dus niet eens een straal van het weiland gegeven.
Ik ben benieuwd of iemand van jullie hier een tip over kan geven.
Alvast bedankt. Yannick
Een boer heeft een cirkelvormig weiland. aan de rand van dat weiland staat een paaltje. aan dat paaltje zit een touw vast waar weer een geit aan zit. Het touw is precies zolang dat de geit precies bij de helft van het totale oppervlakte van het weiland kan. Hoe lang is het touw? Hierbij is dus niet eens een straal van het weiland gegeven.
Ik ben benieuwd of iemand van jullie hier een tip over kan geven.
Alvast bedankt. Yannick
Precies de straal van het weiland ? 
Zonder enig getal kun je er toch echt niet meer mee.
Zonder enig getal kun je er toch echt niet meer mee.
"AAAAAHH ZENNE MOAT, WOARST VLEISCH"
Begint met straal =1 ? Als de straal van het weiland 100 is, is het touw ook 100. Maar maar aangezien er verder niets gegeven is blijft dat gissen.
Het enige wat je met zekerheid kunt zeggen is dat het touw = straal van het weiland.
Het enige wat je met zekerheid kunt zeggen is dat het touw = straal van het weiland.
"AAAAAHH ZENNE MOAT, WOARST VLEISCH"
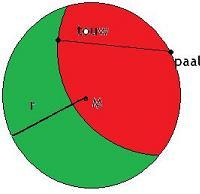
Hierin is het rode en groene deel bij elkaar het weiland, en het rode deel het deel waarin de geit kan grazen. Nu wordt gevraagd naar de lengte van het touw wanneer het groene deel en het rode deel qua oppervlakte gelijk zijn.
volgens mij moet je met een vergelijking op de proppen komen waarbij je dan alleen nog maar de straal hoeft in te vullen om de lengte te weten te komen.
dus eerst de totale oppervlak: pi*straal in kwadraat dat deel je door twee dus
pi*r(kwadraat)
------------------
2
en van daar uit moet je dan gaan zoeken hoe je de opp kunt berekenen aan rand van cirkel etc
dus eerst de totale oppervlak: pi*straal in kwadraat dat deel je door twee dus
pi*r(kwadraat)
------------------
2
en van daar uit moet je dan gaan zoeken hoe je de opp kunt berekenen aan rand van cirkel etc
ze vragen m.i. inderdaad naar een stukje algebra, geen concrete lengte zonder variabele erin.
succes met je huiswerk TS, met dat in ogenschouw genomen is het toch geen moeilijke vraag?
succes met je huiswerk TS, met dat in ogenschouw genomen is het toch geen moeilijke vraag?
Wie haar benen spreidt, spreidt gezelligheid.
Weet ik, ik ken je namelijk.quote:Op woensdag 2 december 2009 21:41 schreef Yannick3211 het volgende:
je bent wel grappig:p heel toevallig had ik een volle 10 voor mijn examen,, 80 van de 80 punten..
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
- [SES FB] Meld nakijkfouten om een hoger cijfer te krijgen -
[ Bericht 76% gewijzigd door GlowMouse op 02-12-2009 21:55:21 (NEE GEEN COLA GEVEN) ]
[ Bericht 76% gewijzigd door GlowMouse op 02-12-2009 21:55:21 (NEE GEEN COLA GEVEN) ]
Dat is een andere manier van formuleren, ik dacht dat het schaap precies bij de helft moest komen xD als in de middellijn kunnen bereiken.quote:
[ afbeelding ]
Hierin is het rode en groene deel bij elkaar het weiland, en het rode deel het deel waarin de geit kan grazen. Nu wordt gevraagd naar de lengte van het touw wanneer het groene deel en het rode deel qua oppervlakte gelijk zijn.
"AAAAAHH ZENNE MOAT, WOARST VLEISCH"
Het punt van die site, die ik ook allang gevonden had, is dat het richting de integraalrekening gaat, en dat krijgen wij pas eind dit jaar, dus zou dat niet in de som gebruikt hoeven te worden.
ik zou zo op het eerste gezicht ook zeggen dat je een parametrisatie maakt voor de oppervlakte van de overlap van de cirkels. Die is afhankelijk van de lengte van het touw van de geit. Dus die oppervlakte stel je dan gelijk aan de halve oppervlakte van het weiland.
Zonder kan ook: http://mathforum.org/library/drmath/view/54871.html of zie http://mathpages.com/home/kmath074/kmath074.htm, maar een exacte oplossing krijg je niet.quote:
Het punt van die site, die ik ook allang gevonden had, is dat het richting de integraalrekening gaat, en dat krijgen wij pas eind dit jaar, dus zou dat niet in de som gebruikt hoeven te worden.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
quote:Op woensdag 2 december 2009 21:08 schreef Yannick3211 het volgende:
Hallo, ik ben student op HBO lerarenopleiding wiskunde, en nou wordt de vraag gesteld:
Een boer heeft een cirkelvormig weiland. aan de rand van dat weiland staat een paaltje. aan dat paaltje zit een touw vast waar weer een geit aan zit. Het touw is precies zolang dat de geit precies bij de helft van het totale oppervlakte van het weiland kan. Hoe lang is het touw? Hierbij is dus niet eens een straal van het weiland gegeven.
Ik ben benieuwd of iemand van jullie hier een tip over kan geven.
Alvast bedankt. Yannick
Ja dag, Die straal is nu net wat je moet berekenen. Als de straal gegeven was zou er geen vraag zijn.quote:Op woensdag 2 december 2009 21:10 schreef znarch het volgende:
Precies de straal van het weiland ?
Lees de vraag nog eens goed door.quote:Op woensdag 2 december 2009 21:14 schreef znarch het volgende:
Begint met straal =1 ? Als de straal van het weiland 100 is, is het touw ook 100. Maar maar aangezien er verder niets gegeven is blijft dat gissen.
Het enige wat je met zekerheid kunt zeggen is dat het touw = straal van het weiland.
De vraag van TS was duidelijk. Het ging om de helft van het oppervlak.quote:Op woensdag 2 december 2009 22:06 schreef znarch het volgende:
[..]
Dat is een andere manier van formuleren, ik dacht dat het schaap precies bij de helft moest komen xD als in de middellijn kunnen bereiken.
edit:
Oeps, ik ben spuit11. Het is alweer 5 december.
"If nothing else works, a total pig-headed unwillingness to look facts in the face will see us through" General Melchett
Klik hier voor uw dagelijkse portie vitaminen.
Klik hier voor uw dagelijkse portie vitaminen.
Ha, ik heb hem zelf opgelost. Ik gebruik een stelsel vergelijkingen. Je gebruikt eerst zo veel mogelijk variabelen, zoals afstand van de lijn tussen de 2 snijpunten tot middelpunt, hoeken van cirkelsectoren etc. Steeds dat schrijven als iets van variabelen die nog meer in de vergelijking staan, dus steeds gaat 1 variabele weg. Omdat de lengte van het touw en de straal van het grasveld lengtematen zijn, is het een recht evenredig verband, dus je kan gewoon in de vergelijkingen invullen r=1. Zo houd je op een gegeven moment een vergelijking met alleen maar "T"tjes, en het valt op mijn niveau nog niet algebraisch op te lossen, je krijgt dit probleem: cos(x) - x = 0. maar goed, dan doe ik het dus met de GR, en dan komt er ongeveer 1,15 uit.
Alleen geldt dat -1 ≤ cos(x) ≤ 1, dus dat cos(x) - x een oplossing geeft met x = 1,15 lijkt me sterk.quote:
Zo houd je op een gegeven moment een vergelijking met alleen maar "T"tjes, en het valt op mijn niveau nog niet algebraisch op te lossen, je krijgt dit probleem: cos(x) - x = 0. maar goed, dan doe ik het dus met de GR, en dan komt er ongeveer 1,15 uit.
Daher iſt die Aufgabe nicht ſowohl, zu ſehn was noch Keiner geſehn hat, als, bei Dem, was Jeder ſieht, zu denken was noch Keiner gedacht hat.
quote:Op dinsdag 15 december 2009 14:55 schreef Yannick3211 het volgende:
...dan doe ik het dus met de GR...
Ik schrijf boeken over wetenschap en filosofie!
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
https://www.epsilon-uitga(...)e-tijd-materie/10996
https://www.spectrumboeke(...)k-niet-9789000386765
https://www.spectrumboeke(...)tronen-9789000395071
Dat cosx - x = 0 was maar een voorbeeld, er wordt ook nog in vermenigvuldigd en zo. De oplossing van mij is 7 paginas lang. De GR bleek trouwens dit ding niet aan te kunnen, dus heb ik met excel ingeklemd. dan kom ik op een waarde van ongeveer 1,158728473. Dit is mijn uiteindelijke vergelijking:
BOOGCOS(1-T^2*(1-COS(2*BOOGCOS(T/2))))/2-SIN((BOOGCOS(1-T^2*(1-COS(2*BOOGCOS(T/2)))))/2)+BOOGCOS(T/2)*T^2= pi/2
BOOGCOS(1-T^2*(1-COS(2*BOOGCOS(T/2))))/2-SIN((BOOGCOS(1-T^2*(1-COS(2*BOOGCOS(T/2)))))/2)+BOOGCOS(T/2)*T^2= pi/2
|
|
