SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Bedankt riparius.
Ik had nog 1 vraag.
Waarom is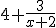 gelijk aan
gelijk aan 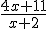
Wat moet je doen om op die 2e te komen?
Ik had nog 1 vraag.
Waarom is
Wat moet je doen om op die 2e te komen?
Crack the following and we will get back to you: !1!llssod000;;


Je hebt hier een constante 4 en een breuk met daarin een variabele x, en die wil je optellen. De clou is nu dat je die constante 4 eerst omzet in een breuk en dan de beide breuken optelt. Maar: breuken kun je alleen optellen als ze gelijknamig zijn, dat wil zeggen als ze dezelfde noemer hebben. Je moet dus die 4 eerst omzetten in een breuk met x+2 als noemer.quote:Op zondag 25 juni 2017 20:24 schreef _--_ het volgende:
Bedankt Riparius.
Ik had nog een vraag.
Waarom isgelijk aan
Wat moet je doen om op die tweede te komen?
Welnu, je kunt gebruik maken van het feit dat een breuk waarvan teller en noemer gelijk zijn de waarde 1 heeft, en als je een getal zoals 4 met 1 vermenigvuldigt dan blijft het 4. We vermenigvuldigen nu die 4 met de breuk (x+2)/(x+2) oftewel 1 en dan hebben we
En zodoende krijgen we voor de som van de constante 4 en de breuk 3/(x+2) dus
Zie je?


Ik heb je verhaal 10 ofzo bestudeerd maar ik snap het nog niet echt.quote:Op zondag 25 juni 2017 20:45 schreef Riparius het volgende:
[..]
Je hebt hier een constante 4 en een breuk met daarin een variabele x, en die wil je optellen. De clou is nu dat je die constante 4 eerst omzet in een breuk en dan de beide breuken optelt. Maar: breuken kun je alleen optellen als ze gelijknamig zijn, dat wil zeggen als ze dezelfde noemer hebben. Je moet dus die 4 eerst omzetten in een breuk met x+2 als noemer.
Welnu, je kunt gebruik maken van het feit dat een breuk waarvan teller en noemer gelijk zijn de waarde 1 heeft, en als je een getal zoals 4 met 1 vermenigvuldigt dan blijft het 4. We vermenigvuldigen nu die 4 met de breuk (x+2)/(x+2) oftewel 1 en dan hebben we
En zodoende krijgen we voor de som van de constante 4 en de breuk 3/(x+2) dus
Zie je?
Crack the following and we will get back to you: !1!llssod000;;


Laten we bij het begin beginnen. Begrijp je datquote:Op zondag 25 juni 2017 21:43 schreef _--_ het volgende:
[..]
Ik heb je verhaal 10 keer of zo bestudeerd maar ik snap het nog niet echt.
voor elke waarde van x ≠ −2 en dat je dus voor elke waarde van x anders dan −2 hebt
?


Dat snap ik. Maar ik snap niet waarom je ×4 doetquote:Op zondag 25 juni 2017 21:58 schreef Riparius het volgende:
[..]
Laten we bij het begin beginnen. Begrijp je dat
voor elke waarde van x ≠ −2 en dat je dus voor elke waarde van x anders dan −2 hebt
?
Crack the following and we will get back to you: !1!llssod000;;


Wel, die 4 is gegeven, want de opdracht was omquote:Op zondag 25 juni 2017 22:01 schreef _--_ het volgende:
[..]
Dat snap ik. Maar ik snap niet waarom je ×4 doet
te herleiden. Ik vermenigvuldig hier niets met 4 maar ik vermenigvuldig die 4 juist met 1 = (x+2)/(x+2). En dat mag ik doen, want als je een grootheid met 1 vermenigvuldigt dan verandert er niets aan die grootheid.
Begrijp je nu waarom je
kunt vervangen door
?


Ja! Tot nu toe heb ik het uigevogeldquote:Op zondag 25 juni 2017 22:25 schreef Riparius het volgende:
[..]
Wel, die 4 is gegeven, want de opdracht was om
te herleiden. Ik vermenigvuldig hier niets met 4 maar ik vermenigvuldig die 4 juist met 1 = (x+2)/(x+2). En dat mag ik doen, want als je een grootheid met 1 vermenigvuldigt dan verandert er niets aan die grootheid.
Begrijp je nu waarom je
kunt vervangen door
?
Crack the following and we will get back to you: !1!llssod000;;


Yepquote:Op zondag 25 juni 2017 22:30 schreef Riparius het volgende:
[..]
OK. Volgende stap dan maar. Begrijp je ook dat je
weer kunt vervangen door
?
Crack the following and we will get back to you: !1!llssod000;;


OK. Haakjes uitwerken in de teller van de eerste breuk geeft 4(x+2) = 4x + 8 zodat jequote:
weer kunt vervangen door
Twee gelijknamige breuken kun je optellen door de tellers op te tellen terwijl de noemer hetzelfde blijft en dan krijg je dus
oftewel
Volkomen helder nu?


Ik ben veel verder nu. Ik snap compleet hoe die stappen in werking gaan, maar ik snap de logica erachter niet. Misschien niet noodzakelijk op de toets maar ik heb altijd de neiging die te moeten weten.quote:Op zondag 25 juni 2017 22:39 schreef Riparius het volgende:
[..]
OK. Haakjes uitwerken in de teller van de eerste breuk geeft 4(x+2) = 4x + 8 zodat je
weer kunt vervangen door
Twee gelijknamige breuken kun je optellen door de tellers op te tellen terwijl de noemer hetzelfde blijft en dan krijg je dus
oftewel
Volkomen helder nu?
Daar doe ik dan zelf wel onderzoek naar
Bedankt!
Crack the following and we will get back to you: !1!llssod000;;


Wat bedoel je precies met de logica erachter? Hoe je op het idee komt welke stappen je moet nemen? Of de stappen zelf?quote:Op zondag 25 juni 2017 22:41 schreef _--_ het volgende:
[..]
Ik ben veel verder nu. Ik snap compleet hoe die stappen in werking gaan, maar ik snap de logica erachter niet. Misschien niet noodzakelijk op de toets maar ik heb altijd de neiging die te moeten weten.
Daar doe ik dan zelf wel onderzoek naar
Bedankt!


Wat is de bedoeling van bijvoorbeeld de 4 x 1 (in breuken)?quote:Op zondag 25 juni 2017 22:45 schreef Riparius het volgende:
[..]
Wat bedoel je precies met de logica erachter? Hoe je op het idee komt welke stappen je moet nemen? Of de stappen zelf?
Ik snap dat je dat moet doen. Maar niet waarom dat goed is. wat zegt de 4x1 hier?
Moeilijk uit te leggen
Crack the following and we will get back to you: !1!llssod000;;


Het is een handigheidje. Je hebt bij deze opgave een getal 4 en een breuk 3/(x+2) en die wil je optellen, althans herleiden tot één breuk. Maar je kunt niet zomaar een getal dat geen breuk is en een breuk bij elkaar optellen. Wat je wél kunt doen is twee breuken bij elkaar optellen. Dus is het idee hier om die 4 eerst om te werken naar een breuk. Maar dat moet niet zomaar een willekeurige breuk zijn, want twee willekeurige breuken kun je nog steeds niet optellen. Wat we nodig hebben zijn twee gelijknamige breuken. En omdat de gegeven breuk 3/(x+2) een noemer (x+2) heeft, moeten we dus zien dat we van die 4 ook een breuk maken met (x+2) als noemer. Dat is wat hier gebeurt.quote:Op zondag 25 juni 2017 22:47 schreef _--_ het volgende:
[..]
Wat is de bedoeling van bijvoorbeeld de 4 x 1 (in breuken)?
Ik snap dat je dat moet doen. Maar niet waarom dat goed is. wat zegt de 4x1 hier?
Moeilijk uit te leggen


Nogmaals bedankt voor je uitlegquote:Op zondag 25 juni 2017 22:54 schreef Riparius het volgende:
[..]
Het is een handigheidje. Je hebt bij deze opgave een getal 4 en een breuk 3/(x+2) en die wil je optellen, althans herleiden tot één breuk. Maar je kunt niet zomaar een getal dat geen breuk is en een breuk bij elkaar optellen. Wat je wél kunt doen is twee breuken bij elkaar optellen. Dus is het idee hier om die 4 eerst om te werken naar een breuk. Maar dat moet niet zomaar een willekeurige breuk zijn, want twee willekeurige breuken kun je nog steeds niet optellen. Wat we nodig hebben zijn twee gelijknamige breuken. En omdat de gegeven breuk 3/(x+2) een noemer (x+2) heeft, moeten we dus zien dat we van die 4 ook een breuk maken met (x+2) als noemer. Dat is wat hier gebeurt.
Crack the following and we will get back to you: !1!llssod000;;


Ik heb een vraagje over mijn rekenmachine. (TI-30XB, gewoon een goedkoop ding).
Als ik sin-1(1/2) ingeef, dan krijg ik keurig als antwoord keurig dertig. Nu wil het ding alleen geen sin-1(-1/2) doen. Ik vraag me af, moet dat niet gewoon min dertig zijn enzovoorts ook, waarom krijg ik een syntax error?
Als ik sin-1(1/2) ingeef, dan krijg ik keurig als antwoord keurig dertig. Nu wil het ding alleen geen sin-1(-1/2) doen. Ik vraag me af, moet dat niet gewoon min dertig zijn enzovoorts ook, waarom krijg ik een syntax error?
"The world will note that the first atomic bomb was dropped on Hiroshima, a military base."


Geen idee, mijn even simpele Casio FX82 doet dat wel gewoon.quote:Op dinsdag 25 juli 2017 17:35 schreef JAM het volgende:
Ik heb een vraagje over mijn rekenmachine. (TI-30XB, gewoon een goedkoop ding).
Als ik sin-1(1/2) ingeef, dan krijg ik keurig als antwoord keurig dertig. Nu wil het ding alleen geen sin-1(-1/2) doen. Ik vraag me af, moet dat niet gewoon min dertig zijn enzovoorts ook, waarom krijg ik een syntax error?
Opinion is the medium between knowledge and ignorance (Plato)


Je vraag is niet te beantwoorden omdat je niet aangeeft welke toetssequenties je in beide gevallen hebt gebruikt. Ik zie wel in de handleiding van het ding dat je bij goniometrische functies en hun inversen wordt geacht een rechterhaakje te gebruiken dat niet matcht met een linkerhaakje (?!). Het gebruik van dit soort toestellen in het onderwijs zou sowieso verboden moeten worden.quote:Op dinsdag 25 juli 2017 17:35 schreef JAM het volgende:
Ik heb een vraagje over mijn rekenmachine. (TI-30XB, gewoon een goedkoop ding).
Als ik sin-1(1/2) ingeef, dan krijg ik keurig als antwoord keurig dertig. Nu wil het ding alleen geen sin-1(-1/2) doen. Ik vraag me af, moet dat niet gewoon min dertig zijn enzovoorts ook, waarom krijg ik een syntax error?


Ik maak even een filmpje. Dan kunnen jullie zien wtf.
"The world will note that the first atomic bomb was dropped on Hiroshima, a military base."


Ik hoop dat het te zien is. Van mijn telefoon opgenomen.
"The world will note that the first atomic bomb was dropped on Hiroshima, a military base."


In ieder geval, arcsin(.5) werkt, arcsin(-.5) niet. Met het n/d knopje hetzelfde verhaal.
"The world will note that the first atomic bomb was dropped on Hiroshima, a military base."


Je gebruikt het verkeerde minteken, denk ik.
Opinion is the medium between knowledge and ignorance (Plato)


Ja. inderdaad. Het euvel is opgelost. Er zit ook zo'n (-) knopje op en dan werkt het wel. Maar zelfs dan..? Min is min? Daar is toch geen ambiguïteit?
"The world will note that the first atomic bomb was dropped on Hiroshima, a military base."


Het verschil tussen de notatie van een negatief getal en een rekenkundige operator is er natuurlijk wel degelijk, zelfs al is het teken hetzelfde en leidt het in de meeste voorkomende gevallen ook nog tot dezelfde uitkomst ook. Casio kiest ervoor om de 'gewone' min ook goed te keuren als het niet tot verwarring kan leiden, TI doet het niet.quote:Op dinsdag 25 juli 2017 19:01 schreef JAM het volgende:
Ja. inderdaad. Het euvel is opgelost. Er zit ook zo'n (-) knopje op en dan werkt het wel. Maar zelfs dan..? Min is min? Daar is toch geen ambiguïteit?
Opinion is the medium between knowledge and ignorance (Plato)

