[Bèta wiskunde] Huiswerk- en vragentopic.

vrijdag 12 januari 2018 @ 22:27:31 #251

Amoeba

Floydiaan.

quote:
Op vrijdag 12 januari 2018 22:20 schreef ronaldoo12 het volgende:

[..]

Hmm.. hoezo zou het mij geen route opleveren? Ik heb één random beginpunt(en om te optimaliseren zou ik dit beginpunt telkens kunnen wijzigen) en vanuit dit beginpunt laat ik sneeuwruimer 1 vertrekken. Doormiddel van het kortste pad algoritme kan ik zien waar hij eindigt nadat hij een uur is bezig geweest. Dit eindpunt is het startpunt van sneeuwruimer 2. Die kiest zijn route op dezelfde wijze zoals sneeuwruimer 1 dat heeft gedaan. Op die manier heeft elk sneeuwruimer zijn eigen route die hij kan doorlopen.

Jazeker kan dat, maar dan moet je nog steeds een eindpunt 'kiezen'. En daarnaast geeft het volgen van zo'n algoritme nog steeds de complicatie dat je dezelfde weg meerdere keren schoon gaat maken.

Nog een tipje, je probleem is equivalent met het 'Route inspection problem' of Chinese Postbodeprobleem. Het goede nieuws is dat het probleem gelukkig niet NP hard is. Op de Engelstalige wiki kun je veel vinden over een mogelijk algoritme.

[ Bericht 2% gewijzigd door Amoeba op 12-01-2018 22:35:57 ]

Fervent tegenstander van het korps lasergamers.

vrijdag 12 januari 2018 @ 22:44:06 #252

ronaldoo12

quote:
Op vrijdag 12 januari 2018 22:27 schreef Amoeba het volgende:

[..]

Jazeker kan dat, maar dan moet je nog steeds een eindpunt 'kiezen'. En daarnaast geeft het volgen van zo'n algoritme nog steeds de complicatie dat je dezelfde weg meerdere keren schoon gaat maken.

Nog een tipje, je probleem is equivalent met het 'Route inspection problem' of Chinese Postbodeprobleem. Het goede nieuws is dat het probleem gelukkig niet NP hard is. Op de Engelstalige wiki kun je veel vinden over een mogelijk algoritme.

Ah super, dan zal ik daar naar gaan kijken. Maar een eis die ik dan stel aan het kortste pad algoritme is dat wegen die al geruimd zijn, niet nog is doorlopen mogen worden tenzij niet anders kan.

[ Bericht 4% gewijzigd door ronaldoo12 op 12-01-2018 22:49:59 ]

vrijdag 12 januari 2018 @ 22:56:43 #253

Amoeba

Floydiaan.

quote:
Op vrijdag 12 januari 2018 22:44 schreef ronaldoo12 het volgende:

[..]

Ah super, dan zal ik daar naar gaan kijken. Maar een eis die ik dan stel aan het kortste pad algoritme is dat wegen die al geruimd zijn, niet nog is doorlopen mogen worden tenzij niet anders kan.

Nogmaals, het is een algoritme om de minimale afstand tussen 2 arbitraire punten in een netwerk te bepalen inclusief route, niet een route die alle punten in het netwerk aandoet.

En als je iets verzint om dat geheugen in te bouwen ga je wel een rekenkundig gedrocht krijgen en blijft van je argument dat je 'cover route' minimaal is weinig over.

Fervent tegenstander van het korps lasergamers.

dinsdag 16 januari 2018 @ 09:50:08 #254

ronaldoo12

Ik heb hier de graaf af van de plattegrond van Delft:

https://imgur.com/a/pihW7

Ik wil dus nu het Chinese postbode algoritme op toepassen maar ik loop een beetje vast met hoe ik het best mijn grafen kan opsplitsen. Ik neem aan dat de sneeuwruimers sneeuw ruimen met een snelheid van 3 km/u. De gemeente Delft wilt nu 3 dingen weten:

1. Het aantal sneeuwruimers dat nodig is om de binnenstad van Delft binnen een uur te ruimen.
2. Het startpunt van elk van deze sneeuwruimers.
3. De route die de sneeuwruimers moeten afleggen.

Ik denk dat al deze drie punten prima te bepalen zijn met het Chinese postbode algoritme. Ik heb zelf bedacht om grafen te maken met een gewicht van maximaal 2800m zodat er 200m speling overblijft voor de wegen die dubbel moeten worden bewandeld. Ik weet alleen niet of dit ideaal is.

dinsdag 16 januari 2018 @ 11:27:57 #255

-jos-

Money=Power

quote:
Op dinsdag 16 januari 2018 09:50 schreef ronaldoo12 het volgende:
Ik heb hier de graaf af van de plattegrond van Delft:

https://imgur.com/a/pihW7

Ik wil dus nu het Chinese postbode algoritme op toepassen maar ik loop een beetje vast met hoe ik het best mijn grafen kan opsplitsen.

Dat hoef jij niet te doen, dat doet het algoritme voor je.

Ik neem aan dat je kennis hebt van graaftheorie? Een beschrijving (van de simpele versie) van je probleem wordt hier gegeven: https://en.wikipedia.org/(...)#Undirected_solution
De versie die jij probeert op te lossen is het meer algemene k-Chinese postman probleem.

quote:
Ik neem aan dat de sneeuwruimers sneeuw ruimen met een snelheid van 3 km/u. De gemeente Delft wilt nu 3 dingen weten:

1. Het aantal sneeuwruimers dat nodig is om de binnenstad van Delft binnen een uur te ruimen.
2. Het startpunt van elk van deze sneeuwruimers.
3. De route die de sneeuwruimers moeten afleggen.

Ik denk dat al deze drie punten prima te bepalen zijn met het Chinese postbode algoritme. Ik heb zelf bedacht om grafen te maken met een gewicht van maximaal 2800m zodat er 200m speling overblijft voor de wegen die dubbel moeten worden bewandeld. Ik weet alleen niet of dit ideaal is.

Waarom zou je meerdere grafen willen maken?

WEB / [HaxBall #64] Jos is God
Arguing on the Internet is like running in the Special Olympics.

dinsdag 16 januari 2018 @ 11:37:31 #256

ronaldoo12

quote:
Op dinsdag 16 januari 2018 11:27 schreef -jos- het volgende:

[..]

Dat hoef jij niet te doen, dat doet het algoritme voor je.

Ik neem aan dat je kennis hebt van graaftheorie? Een beschrijving (van de simpele versie) van je probleem wordt hier gegeven: https://en.wikipedia.org/(...)#Undirected_solution
De versie die jij probeert op te lossen is het meer algemene k-Chinese postman probleem.

[..]

Waarom zou je meerdere grafen willen maken?

Omdat ik voor ieder sneeuwruimer moet bepalen welk route hij moet bewandelen. Elk sneeuwruimer krijgt dus zijn eigen graaf toegewezen. Daarnaast mag de afstand die hij beloopt niet groter zijn dan 3000m omdat dat de afstand is die hij aflegt binnen 1 uur.

dinsdag 16 januari 2018 @ 11:49:09 #257

-jos-

Money=Power

quote:
Op dinsdag 16 januari 2018 11:37 schreef ronaldoo12 het volgende:

[..]

Omdat ik voor ieder sneeuwruimer moet bepalen welk route hij moet bewandelen. Elk sneeuwruimer krijgt dus zijn eigen graaf toegewezen. Daarnaast mag de afstand die hij beloopt niet groter zijn dan 3000m omdat dat de afstand is die hij aflegt binnen 1 uur.

Je kunt dit probleem niet zomaar opsplitsen in kleinere deelproblemen aangezien de oplossing voor een sneeuwruimer afhankelijk is van de oplossingen voor andere sneeuwruimers.

Voor wat voor soort vak is deze opdracht? Heb je kennis van graaftheorie en van algoritmes?

WEB / [HaxBall #64] Jos is God
Arguing on the Internet is like running in the Special Olympics.

dinsdag 16 januari 2018 @ 11:58:38 #258

ronaldoo12

quote:
Op dinsdag 16 januari 2018 11:49 schreef -jos- het volgende:

[..]

Je kunt dit probleem niet zomaar opsplitsen in kleinere deelproblemen aangezien de oplossing voor een sneeuwruimer afhankelijk is van de oplossingen voor andere sneeuwruimers.

Voor wat voor soort vak is deze opdracht? Heb je kennis van graaftheorie en van algoritmes?

Voor een wiskundig praktijkopdracht, een project is 't. Heb wel wat kennis van graaftheorie en algoritmes maar niet gigantisch veel. Ik heb nu bijna de afstand van elk zijde bepaald. Het is voor mij 't belangrijkste dat ik met een oplossing kom, dat dit niet de meest ideale is maakt me niet heel veel uit. Het Chinese postbode algoritme schijnt hier heel goed bij te passen. Ik wil er nu alleen nog voor zorgen dat ik dit algoritme zo goed mogelijk toepas.

donderdag 18 januari 2018 @ 13:17:15 #259

Mandarinho

Hoe herleid ik 2(4-a)^2-1/3(4-a)^3-1/2a(4-a)^2?

donderdag 18 januari 2018 @ 18:11:49 #260

Riparius

quote:
Op donderdag 18 januari 2018 13:17 schreef Mandarinho het volgende:
Hoe herleid ik 2(4-a)^2-1/3(4-a)^3-1/2a(4-a)^2?

Je hebt

$2(4\,-\,a)^2\,-\,\frac{1}{3}(4\,-\,a)^3\,-\,\frac{1}{2}a(4\,-\,a)^2$

Je kunt beginnen met te bedenken dat je drie termen hebt die een factor (4−a)² gemeen hebben, en deze gemene factor kun je buiten haakjes halen, dan krijgen we

$(4\,-\,a)^2\left(2\,-\,\frac{1}{3}(4\,-\,a)\,-\,\frac{1}{2}a\right)$

Na uitwerken van ⅓(4−a) geeft dit

$(4\,-\,a)^2\left(2\,-\,\frac{4}{3}\,+\,\frac{1}{3}a\,-\,\frac{1}{2}a\right)$

en dus

$(4\,-\,a)^2\left(\frac{2}{3}\,-\,\frac{1}{6}a\right)$

Nu kun je bedenken dat 2/3 = 4/6. Halen we dus bij (⅔ − ⅙a) een factor ⅙ buiten haakjes, dan hebben we (⅔ − ⅙a) = ⅙(4 − a) zodat we krijgen

$\frac{1}{6}(4\,-\,a)^2(4\,-\,a)$

oftewel

$\frac{1}{6}(4\,-\,a)^3$

That's all.

[ Bericht 0% gewijzigd door Riparius op 18-01-2018 18:59:45 ]

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

zaterdag 20 januari 2018 @ 15:51:40 #261

Mandarinho

quote:
Op donderdag 18 januari 2018 18:11 schreef Riparius het volgende:

[..]

Je hebt

$2(4\,-\,a)^2\,-\,\frac{1}{3}(4\,-\,a)^3\,-\,\frac{1}{2}a(4\,-\,a)^2$

Je kunt beginnen met te bedenken dat je drie termen hebt die een factor (4−a)² gemeen hebben, en deze gemene factor kun je buiten haakjes halen, dan krijgen we

$(4\,-\,a)^2\left(2\,-\,\frac{1}{3}(4\,-\,a)\,-\,\frac{1}{2}a\right)$

Na uitwerken van ⅓(4−a) geeft dit

$(4\,-\,a)^2\left(2\,-\,\frac{4}{3}\,+\,\frac{1}{3}a\,-\,\frac{1}{2}a\right)$

en dus

$(4\,-\,a)^2\left(\frac{2}{3}\,-\,\frac{1}{6}a\right)$

Nu kun je bedenken dat 2/3 = 4/6. Halen we dus bij (⅔ − ⅙a) een factor ⅙ buiten haakjes, dan hebben we (⅔ − ⅙a) = ⅙(4 − a) zodat we krijgen

$\frac{1}{6}(4\,-\,a)^2(4\,-\,a)$

oftewel

$\frac{1}{6}(4\,-\,a)^3$

That's all.

Helder, bedankt. Toch weer twee handige dingen geleerd.

zaterdag 20 januari 2018 @ 19:59:10 #262

Amoeba

Floydiaan.

quote:
Op dinsdag 16 januari 2018 11:58 schreef ronaldoo12 het volgende:

[..]

Voor een wiskundig praktijkopdracht, een project is 't. Heb wel wat kennis van graaftheorie en algoritmes maar niet gigantisch veel. Ik heb nu bijna de afstand van elk zijde bepaald. Het is voor mij 't belangrijkste dat ik met een oplossing kom, dat dit niet de meest ideale is maakt me niet heel veel uit. Het Chinese postbode algoritme schijnt hier heel goed bij te passen. Ik wil er nu alleen nog voor zorgen dat ik dit algoritme zo goed mogelijk toepas.

Ook zoiets getuigt weer van weinig inzicht, want de oplossing van je probleem was nou net per definitie de optimale.

Een oplossing van het Chinese Postbode Probleem is zo'n Euclidean Tour, dat zou inderdaad een route voor één sneeuwruimer geven die je dan vervolgens kunt splitten in afzonderlijke routes.

Fervent tegenstander van het korps lasergamers.

zondag 21 januari 2018 @ 10:08:11 #263

ronaldoo12

quote:
Op zaterdag 20 januari 2018 19:59 schreef Amoeba het volgende:

[..]

Ook zoiets getuigt weer van weinig inzicht, want de oplossing van je probleem was nou net per definitie de optimale.

Een oplossing van het Chinese Postbode Probleem is zo'n Euclidean Tour, dat zou inderdaad een route voor één sneeuwruimer geven die je dan vervolgens kunt splitten in afzonderlijke routes.

Klopt het is inmiddels gelukt(Y).

zondag 21 januari 2018 @ 10:10:47 #264

ronaldoo12

Ik vroeg me af of iemand me kan helpen met dit algoritme vertalen naar eenvoudig Nederlandse taal:

https://imgur.com/a/oZUYt

De eerste stap: Geef A het label (-,0). Houdt dit in dat A verbonden is met (geen knopen, 0 takken) Op die manier?

zondag 21 januari 2018 @ 13:16:49 #265

Amoeba

Floydiaan.

quote:
Op zondag 21 januari 2018 10:10 schreef ronaldoo12 het volgende:
Ik vroeg me af of iemand me kan helpen met dit algoritme vertalen naar eenvoudig Nederlandse taal:

https://imgur.com/a/oZUYt

De eerste stap: Geef A het label (-,0). Houdt dit in dat A verbonden is met (geen knopen, 0 takken) Op die manier?

Nee de afstand van A naar A is 0. Dijkstra's algoritme vindt het kortste pad volgens de volgende methode.

Kijk naar alle buren u van A en bereken d(u,a)

Daarna naar alle buren x van u en bereken d(x,u) + d(a,u), stel dat x meerdere malen voorkomt. Als d(x,v) als eens berekend was voor een bepaalde v kies dan de minimum afstand van de twee (dus of de kortste route van A naar x via v of u gaat).

Bij een gelijke afstand wordt altijd uniform gekozen.

Dit gaat door tot Z gevonden is en Dijkstra's algoritme vindt, inderdaad, de kortste afstand van A naar Z.

Dit werkt in ieder geval voor een verbonden graaf. Als je dit programmeert zet je alle afstanden in het begin naar +∞, omdat null en een Real niet zo goed vergelijken.

Fervent tegenstander van het korps lasergamers.

maandag 22 januari 2018 @ 19:08:43 #266

Amoeba

Floydiaan.

Ik heb ook vraag.

Even een paar opmerkingen, de dimensie van X is mogelijk oneindig, B(X) is de ruimte van alle begrensde, lineare operatoren op X, p(T) is de resolvent set en o(T) is het spectrum.

a,b,c,d heb ik eigenlijk zo goed als bewezen. Het bewijs van e) gaat in grote lijnen zo (volgens contradictie)

Dus D' = D intersection p(T) is niet leeg, maar ook niet gelijk aan D.

Kies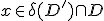 $x \in \delta(D') \cap D$ (dus in de boundary van D')

Het idee is nu om uit 3d te concluderen dat dit niet kan, dus het euvel is nu om het bestaan van een rij (x_n) aan te tonen met limiet x en uit d) te halen dat x in D' zit. Dat is een consequentie van het volgende argument:

D' is open.

Dus dat betekent o.a. direct dat x niet in p(T) zit, waaruit direct de tegenspraak volgt, immers volgens d) betekent de rij in D' naar x dat x wel in p(T) zit.

Waarom is D' open? Volgens mij is p(T) gesloten in D, D zelf is open dus ik zie niet zo snel waarom die intersection ook open is.

Fervent tegenstander van het korps lasergamers.

maandag 22 januari 2018 @ 20:49:47 #267

thabit

Ik zit zelf niet zo in de functionaalanalyse, maar ik zou denken dat je (c) kunt gebruiken daarvoor.

maandag 22 januari 2018 @ 21:13:48 #268

Amoeba

Floydiaan.

quote:
Op maandag 22 januari 2018 20:49 schreef thabit het volgende:
Ik zit zelf niet zo in de functionaalanalyse, maar ik zou denken dat je (c) kunt gebruiken daarvoor.

Ik heb even wat rondgevraagd en een van de eigenschappen van p(T) is dat het altijd een open subset van C is, en eindige intersecties van opens zijn weer open, dus topologisch gezien zit het dan wel juist. Ik zie alleen mijn eigen logische fout helaas nog niet zo in als ik zeg dat p(T) gesloten is in D.

Analysevakken zijn over het algemeen de moeilijkste wiskundevakken (in ieder geval qua tentamen), aangezien mijn major in de richting van stochastiek is en ik een aantal keuzevakken uit andere tracks moet hebben kies ik meestal die analysevakken zoals Partial Differential Equations, Topologie, Functionaal Analyse, etc. Dat je qua curriculum in ieder geval nog kan zeggen dat je het jezelf niet te makkelijk hebt gemaakt.

Iedereen op de TU/e kan tegenwoordig een bachelor Applied Mathematics krijgen terwijl je bijna de helft van je vakken bij andere faculteiten mag volgen.

[ Bericht 3% gewijzigd door Amoeba op 22-01-2018 21:20:22 ]

Fervent tegenstander van het korps lasergamers.

maandag 22 januari 2018 @ 21:34:31 #269

thabit

quote:
Op maandag 22 januari 2018 21:13 schreef Amoeba het volgende:

[..]

Ik heb even wat rondgevraagd en een van de eigenschappen van p(T) is dat het altijd een open subset van C is, en eindige intersecties van opens zijn weer open, dus topologisch gezien zit het dan wel juist. Ik zie alleen mijn eigen logische fout helaas nog niet zo in als ik zeg dat p(T) gesloten is in D.

Dat is ook niet fout. Het is zowel open als gesloten in D, dus de doorsnede is heel D of leeg.

maandag 22 januari 2018 @ 21:47:29 #270

Amoeba

Floydiaan.

quote:
Op maandag 22 januari 2018 21:34 schreef thabit het volgende:

[..]

Dat is ook niet fout. Het is zowel open als gesloten in D, dus de doorsnede is heel D of leeg.

Ja klopt, een andere manier om eigenlijk op te merken dat er een contradictie is. Had ik natuurlijk wel moeten weten dat die ook open is.

Fervent tegenstander van het korps lasergamers.

maandag 22 januari 2018 @ 21:51:33 #271

thabit

Maar is dat bij (c) niet een open conditie op λ?

maandag 22 januari 2018 @ 21:53:02 #272

Amoeba

Floydiaan.

quote:
Op maandag 22 januari 2018 21:51 schreef thabit het volgende:
Maar is dat bij (c) niet een open conditie op λ?

Surjectiviteit impliceert dat λ - T een open mapping is.

Kun je daaruit concluderen dat p(T) open is?

Ik heb overigens een dictaat/boek waarin een lemma staat dat p(T) een open subset is, het bewijs laat zien dat er een power series representation van de resolvent bestaat die convergent is op een open subset van C rondom een punt in p(T).

$(\lambda - T)^{-1} =: R(\lambda,T) = \sum_{n \in \mathbb{N}} (\lambda_0 - \lambda)^n R(\lambda_0,T)^{n+1}$

Als je dat weet moet p(T) wel open zijn aangezien een topologie gesloten is onder willekeurige verenigingen

[ Bericht 8% gewijzigd door Amoeba op 22-01-2018 22:07:14 ]

Fervent tegenstander van het korps lasergamers.

woensdag 7 maart 2018 @ 20:56:12 #273

_--_

In varietate concordia

Heeft iemand enig idee waar ik een zo simpel mogelijke bewijs kan vinden dat het argument dat Fermatgetallen alleen uit priemgetallen bestaat ontkracht? Behalve dat je het manueel invult.