SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
[ Bericht 98% gewijzigd door motorbloempje op 13-12-2015 19:13:34 ]
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
[ Bericht 98% gewijzigd door motorbloempje op 13-12-2015 19:13:34 ]
Ja doei.


Ik ben opzoek naar iemand die bijles kan geven met wiskunde b niveau
Zit in mijn propedeuse omgeving zuid Holland
Iemand tips ??
Zit in mijn propedeuse omgeving zuid Holland
Iemand tips ??


Niet hier. Aanbieden van of vragen om betaalde diensten is niet toegestaan op FOK. Je kunt hier uiteraard wel vragen stellen over opgaven of over 'theorie' of concepten waar je moeite mee hebt.quote:Op zondag 13 december 2015 15:01 schreef klawie het volgende:
Ik ben opzoek naar iemand die bijles kan geven met wiskunde b niveau
Zit in mijn propedeuse omgeving zuid Holland
Iemand tips ??


Je mag best vragen of iemand toevallig ervaring heeft met Studiehulp in een bepaalde regio. Je eigen diensten aanbieden of direct iemand vragen mag niet.
Ja doei.


ik zou eens kijken of er studenten aan je lokale universiteit te vinden zijn bij de exacte studies die bijles aanbieden? Even navragen bij de studievereniging van bijvoorbeeld wiskunde/informatica/natuurkunde ofzo.quote:Op zondag 13 december 2015 15:01 schreef klawie het volgende:
Ik ben opzoek naar iemand die bijles kan geven met wiskunde b niveau
Zit in mijn propedeuse omgeving zuid Holland
Iemand tips ??
Ja doei.


Op school had ik het al nagevraagd en ik ik zit niet bij een studenten corp
Maar ging mij meer of iemand toevallig goeie ervaringen had met iets of iemand
Maar ging mij meer of iemand toevallig goeie ervaringen had met iets of iemand


Jij hoeft toch niet bij een 'corp'(? Wat heeft dat met een studievereniging te maken?) te zitten om bij een andere studievereniging te vragen of zij mensen kennen die bijles geven?
Ja doei.


Weet iemand hoe ik de volgende formule kan differentiëren naar: d σ² / d xa ?
σ² = 0,06² *xa² + 0,04² * (1-xa)² + 2*xa * (1-xa) * 0,5*0,04*0,06
Ik moet uitkomen op 0,0056xa - 0,0008.
Hoe ik de tweede en derde term moet differentiëren ben ik een tikkeltje vergeten. Ik wou voor het gemak even allereerst alles netjes uitschrijven, maar toen kwam ik uit op :
0,0012xa² - 0,0032(1-xa) + 0,0024xa
Maar dat moet fout zijn, aangezien uitschrijven het volgende moet opleveren:
Ik ben dus benieuwd naar de methodiek van zo snel mogelijk differentiëren (zonder uitschrijven) en naar de uitschrijfmethodiek.
σ² = 0,06² *xa² + 0,04² * (1-xa)² + 2*xa * (1-xa) * 0,5*0,04*0,06
Ik moet uitkomen op 0,0056xa - 0,0008.
Hoe ik de tweede en derde term moet differentiëren ben ik een tikkeltje vergeten. Ik wou voor het gemak even allereerst alles netjes uitschrijven, maar toen kwam ik uit op :
0,0012xa² - 0,0032(1-xa) + 0,0024xa
Maar dat moet fout zijn, aangezien uitschrijven het volgende moet opleveren:
Ik ben dus benieuwd naar de methodiek van zo snel mogelijk differentiëren (zonder uitschrijven) en naar de uitschrijfmethodiek.


Het kan inderdaad door uitschrijven, of door het gebruiken van de produkt- en kettingregel. Als je daarbij niet uitkomt op het goede antwoord, is de meest voor de hand liggende optie dat je bij al die nare getallen ergens een rekenfoutje hebt gemaakt.
0,06² *xa² + 0,04² * (1-xa)² + 2*xa * (1-xa) * 0,5*0,04*0,06
=
0,0036xa² + 0,0016(1-xa)² + 0,0024xa(1-xa)
=
0,0036xa² + 0,0016 (1-2xa+xa²) + 0,0024(xa-xa²)
=
0,0036xa² + 0,0016 - 0,0032xa + 0,0016xa² + 0,0024xa - 0,0024xa²
=
0,0028xa² - 0,0008xa + 0,0016
Check.
0,06² *xa² + 0,04² * (1-xa)² + 2*xa * (1-xa) * 0,5*0,04*0,06
=
0,0036xa² + 0,0016(1-xa)² + 0,0024xa(1-xa)
=
0,0036xa² + 0,0016 (1-2xa+xa²) + 0,0024(xa-xa²)
=
0,0036xa² + 0,0016 - 0,0032xa + 0,0016xa² + 0,0024xa - 0,0024xa²
=
0,0028xa² - 0,0008xa + 0,0016
Check.
Opinion is the medium between knowledge and ignorance (Plato)


Op die fiets dacht dat je bij een corp moest zitten om gebruik te maken van die diensten zeg maarquote:Op zondag 13 december 2015 20:05 schreef motorbloempje het volgende:
Jij hoeft toch niet bij een 'corp'(? Wat heeft dat met een studievereniging te maken?) te zitten om bij een andere studievereniging te vragen of zij mensen kennen die bijles geven?
Maar por morgen een aantal mensen in hun zij top!


Dat is onbegrijpelijk, want je hebt de bekende regels voor het differentiëren toch geleerd en er ook tentamen in gedaan?quote:Op zondag 13 december 2015 20:47 schreef RustCohle het volgende:
Weet iemand hoe ik de volgende formule kan differentiëren naar d σ² / d xa xA?
σ² = 0,06² *xA² + 0,04² * (1-xA)² + 2*xA * (1-xA) * 0,5*0,04*0,06
Ik moet uitkomen op 0,0056xA - 0,0008.
Hoe ik de tweede en derde term moet differentiëren ben ik een tikkeltje vergeten.
Hier is dat nog gemakkelijk te doen, maar stel dat er een term met (1−xA)10 in je uitdrukking had gezeten, dan is uitschrijven niet goed meer te doen terwijl direct differentiëren nog even gemakkelijk is. Geen goed plan dus.quote:Ik wou voor het gemak even allereerst alles netjes uitschrijven,
Ik heb eens even naar de uitdrukking zitten kijken die je zelf had gevonden om te zien hoe je daar op bent gekomen, en dat is mij helaas maar al te duidelijk geworden.quote:maar toen kwam ik uit op :
0,0012xA² - 0,0032(1-xA) + 0,0024xA
Maar dat moet fout zijn, aangezien uitschrijven het volgende moet opleveren:
[ afbeelding ]
Je bent kennelijk begonnen met 0,06²·xA² = 0,0036·xA² en je hebt daar 2·xA·xA·0,5·0,04·0,06 = 0,0024·xA² uit de derde term vanaf getrokken om op 0,0012·xA² uit te komen. Maar dat impliceert dat je helemaal niet hebt gezien dat
0,04²·(1−xA)²
ook nog eens een term 0,0016·xA² oplevert bij uitwerken, zodat we 0,0012·xA² + 0,0016·xA² = 0,0028·xA² krijgen.
Kennelijk verkeer je in de veronderstelling dat 0,04²·(1−xA)² hetzelfde zou zijn als
0,0032·(1−xA)
want dat is de tweede term in je uitwerking. Je kent dus na meer dan een jaar nog steeds niet je merkwaardige producten. En dan ben je ook nog vergeten dat uitwerken van de haakjes van de derde term behalve een kwadratische term ook nog een lineaire term oplevert.
Er zit niets anders op dan de regels voor het differentiëren en voor het uitvoeren van algebraïsche herleidingen te blijven oefenen, net zolang totdat je ze vlot en foutloos uit kunt voeren. Voor deze opgave kun je je trouwens foutgevoelige berekeningen met die decimale breuken besparen door eerst even een factor 10−4 buiten haakjes te halen, dan krijg jequote:Ik ben dus benieuwd naar de methodiek van zo snel mogelijk differentiëren (zonder uitschrijven) en naar de uitschrijfmethodiek.
differentiëren naar xA geeft dan


Dit convergeert naar
(De gehele vraag is om aan te tonen


Een oneindig product waarvan elke factor uit een som van twee termen bestaat is lastig te hanteren, dus het idee is om deze som om te zetten in een product zodat we het oneindige product om kunnen zetten in een product van oneindige producten die elk afzonderlijk beter zijn te hanteren. Je kuntquote:Op dinsdag 15 december 2015 11:16 schreef Novermars het volgende:
Dit convergeert naar, maar iemand enig idee hoe dit aan te tonen?
herschrijven als
en dan bij
een factor
buiten haakjes halen, zodat we krijgen
oftewel
en daarmee
Het eerste van deze oneindige producten is gemakkelijk te bepalen, aangezien exponenten optellen bij vermenigvuldiging van machten van hetzelfde grondtal, zodat dit neerkomt op het sommeren van een oneindige meetkundige reeks met reden ½, die uiteraard convergeert.
Voor het tweede oneindige product kun je gebruik maken van het bekende resultaat
waarvan je hier een eenvoudig bewijs kunt vinden.
Een oneindige meetkundige reeks met als eerste term ¼it en met als reden ½ heeft als som ½it, dus hebben we
en verder hebben we (voor t ≠ 0)
zodat je oneindige product dus convergeert naar
QED
[ Bericht 1% gewijzigd door Riparius op 18-12-2015 02:58:01 ]


Mijn complimenten, ik was er zelf niet opgekomen om de som in een product om te zetten. Ik zocht wel in de richting van goniometrische functies, maar was de sinc identity nog niet tegen gekomen, in het vervolg misschien ook maar in het Duits googelen!quote:
Bedankt!


Ik heb soms moeite met het snappen van de notatie, neem bijvoorbeeld dit stukje: https://www.dropbox.com/s(...)%2017-03-36.png?dl=0
Wat wordt er bijvoorbeeld bedoeld met 'beschouw voor elke n in N de verzameling B_n ...'?
Heeft iemand tips om de notatie beter te snappen?
Wat wordt er bijvoorbeeld bedoeld met 'beschouw voor elke n in N de verzameling B_n ...'?
Heeft iemand tips om de notatie beter te snappen?


Ze definiëren Bn := (0, n] voor elke n ∈ ℕ zodat elke Bn dus een half open half gesloten interval is op ℝ. Een interval op ℝ is een verzameling reële getallen zodat elke Bn dus een deelverzameling is van ℝ. Heb je wel eens wat over verzamelingenleer en de daarbij gebruikte notaties gehad op school?quote:Op maandag 21 december 2015 17:05 schreef netchip het volgende:
Ik heb soms moeite met het snappen van de notatie, neem bijvoorbeeld dit stukje: https://www.dropbox.com/s(...)%2017-03-36.png?dl=0
Wat wordt er bijvoorbeeld bedoeld met 'beschouw voor elke n in N de verzameling B_n ...'?
Heeft iemand tips om de notatie beter te snappen?


Waarom is U_n ∈ ℕ B_n = (0, oneindig)? Stel dat we n = 5 kiezen, dan krijgen we toch (0, 5] en toch geen (0, oneindig)?quote:Op maandag 21 december 2015 17:17 schreef Riparius het volgende:
[..]
Ze definiëren Bn := (0, n] voor elke n ∈ ℕ zodat elke Bn dus een half open half gesloten interval is op ℝ. Een interval op ℝ is een verzameling reële getallen zodat elke Bn dus een deelverzameling is van ℝ. Heb je wel eens wat over verzamelingenleer en de daarbij gebruikte notaties gehad op school?
Verzamelingenleer heb ik niet gehad op school, ik doe dit in m'n vrije tijd.


Het gaat hier over de vereniging (Engels: union) van alle verzamelingen Bn met n ∈ ℕ. En die vereniging bestaat uit alle positieve reële getallen.quote:Op maandag 21 december 2015 17:48 schreef netchip het volgende:
[..]
Waarom is U_n ∈ ℕ B_n = (0, oneindig)? Stel dat we n = 5 kiezen, dan krijgen we toch (0, 5] en toch geen (0, oneindig)?
Begin eens even met dit artikel en ook dit artikel in Wikipedia.quote:Verzamelingenleer heb ik niet gehad op school, ik doe dit in m'n vrije tijd.


Ik heb een paar korte vragen over encryptie.
Ik begrijp wat encryptie met behulp van een rotatie is (Caesar), namelijk gewoon alle letters een aantal posities opgeschoven. Ik meen me te herinneren dat je dat kunt schrijven als
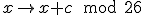
Maar dit ontcijferen is zeer eenvoudig.
Een ietwat meer geavanceerde encryptiemethode is
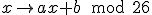
Ik geloof dat deze encryptie bekend is onder de naam Vigenère, klopt dat?
En klopt het dat je de sleutel (de natuurlijke getallen a en b) kunt verkrijgen als je van twee letters weet op welke letters zij worden afgebeeld?
Mijn derde vraag gaat over de volgende encryptiemethode waarbij het alfabet wordt gegeven door:
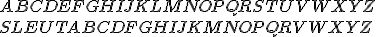
Oftewel dat de eerste letters worden afgebeeld op een sleutelwoord (hier: sleutel) en de overige letters staan op alfabetische volgorde.
Ik ben benieuwd hoe deze encryptiemethode heet (ik wil er graag meer over weten), en hoe goed is deze encryptymethode?
Ik begrijp wat encryptie met behulp van een rotatie is (Caesar), namelijk gewoon alle letters een aantal posities opgeschoven. Ik meen me te herinneren dat je dat kunt schrijven als
Maar dit ontcijferen is zeer eenvoudig.
Een ietwat meer geavanceerde encryptiemethode is
Ik geloof dat deze encryptie bekend is onder de naam Vigenère, klopt dat?
En klopt het dat je de sleutel (de natuurlijke getallen a en b) kunt verkrijgen als je van twee letters weet op welke letters zij worden afgebeeld?
Mijn derde vraag gaat over de volgende encryptiemethode waarbij het alfabet wordt gegeven door:
Oftewel dat de eerste letters worden afgebeeld op een sleutelwoord (hier: sleutel) en de overige letters staan op alfabetische volgorde.
Ik ben benieuwd hoe deze encryptiemethode heet (ik wil er graag meer over weten), en hoe goed is deze encryptymethode?


Het is inderdaad een kwestie van proberen van wat getallen, als je er twee weet.quote:Op zaterdag 26 december 2015 17:18 schreef mr.wout het volgende:
Ik heb een paar korte vragen over encryptie.
Ik begrijp wat encryptie met behulp van een rotatie is (Caesar), namelijk gewoon alle letters een aantal posities opgeschoven. Ik meen me te herinneren dat je dat kunt schrijven als
Maar dit ontcijferen is zeer eenvoudig.
Een ietwat meer geavanceerde encryptiemethode is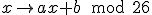
Ik geloof dat deze encryptie bekend is onder de naam Vigenère, klopt dat?
En klopt het dat je de sleutel (de natuurlijke getallen a en b) kunt verkrijgen als je van twee letters weet op welke letters zij worden afgebeeld?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Integreren over snelheid v(x) geeft de afstand over een tijd.
Wat geeft integreren over acceleratie a(x) en integreren over f(x)?
Bedankt alvast!
Wat geeft integreren over acceleratie a(x) en integreren over f(x)?
Bedankt alvast!


Je moet nog maar eens goed in je wis- en natuurkundeboeken bladeren om na te kijken hoe je dit precies moet formuleren, want dit verdient niet direct de schoonheidsprijs.quote:Op dinsdag 5 januari 2016 16:16 schreef obsama het volgende:
Integreren over snelheid v(x) geeft de afstand over een tijd.
Wat geeft integreren over acceleratie a(x) en integreren over f(x)?
Bedankt alvast!
Maar wat je waarschijnlijk wil weten is dat het integreren van de acceleratie normaal gesproken de snelheid oplevert. Echter, net zo normaal gesproken zijn dat allemaal functies met de tijd (t) als variabele, en niet x (afstand).
v(t) = x'(t), a(t) = v'(t)
En wat f(x) zou betekenen staat niet in je post. In zijn algemeenheid gebruik je het integreren van f(x) om de oppervlakte onder de grafiek van f te bepalen. Wat die uitkomst betekent, is geheel afhankelijk van je context.
Opinion is the medium between knowledge and ignorance (Plato)


Ja sorry wat te snel verwoord. Wat ik bedoel is het volgende:quote:Op dinsdag 5 januari 2016 16:50 schreef Janneke141 het volgende:
[..]
Je moet nog maar eens goed in je wis- en natuurkundeboeken bladeren om na te kijken hoe je dit precies moet formuleren, want dit verdient niet direct de schoonheidsprijs.
Maar wat je waarschijnlijk wil weten is dat het integreren van de acceleratie normaal gesproken de snelheid oplevert. Echter, net zo normaal gesproken zijn dat allemaal functies met de tijd (t) als variabele, en niet x (afstand).
v(t) = x'(t), a(t) = v'(t)
En wat f(x) zou betekenen staat niet in je post. In zijn algemeenheid gebruik je het integreren van f(x) om de oppervlakte onder de grafiek van f te bepalen. Wat die uitkomst betekent, is geheel afhankelijk van je context.
Als ik de integraal tussen t1=0 en t2=5 neem van v(x) en de eenheid is meter per seconde dan is de uitkomst toch gewoon de afstand die ik heb afgelegd tussen t1 en t2 in meters per seconde?
Wat nou als ik de integraal neem van t1=0 en t2=5 van a(x), wat stelt het getal dat daar uitkomt dan voor?
Sorry voor het houtje touwtje bericht, ik hoop dat het zo iets duidelijker is.


Waarom volg je mijn tip niet op en gebruik je de tijd t als variabele? Je maakt jezelf nogal in de war door dat niet te doen.quote:Op dinsdag 5 januari 2016 16:57 schreef obsama het volgende:
[..]
Ja sorry wat te snel verwoord. Wat ik bedoel is het volgende:
Als ik de integraal tussen t1=0 en t2=5 neem van v(x) en de eenheid is meter per seconde dan is de uitkomst toch gewoon de afstand die ik heb afgelegd tussen t1 en t2 in meters per seconde?
Wat nou als ik de integraal neem van t1=0 en t2=5 van a(x), wat stelt het getal dat daar uitkomt dan voor?
Sorry voor het houtje touwtje bericht, ik hoop dat het zo iets duidelijker is.
Het levert je als uitkomst niet de gemiddelde snelheid tussen t1 en t2
[ Bericht 5% gewijzigd door Janneke141 op 05-01-2016 17:46:33 ]
Opinion is the medium between knowledge and ignorance (Plato)


Nee, want ½(v(t1) + v(t2)) is in het algemeen iets anders dan v(t2) − v(t1).quote:Op dinsdag 5 januari 2016 16:57 schreef Janneke141 het volgende:
[..]
Het levert je als uitkomst de gemiddelde snelheid tussen t1 en t2.


quote:Op dinsdag 5 januari 2016 17:45 schreef Riparius het volgende:
[..]
Nee, want ½(v(t1) + v(t2)) is in het algemeen iets anders dan v(t2) − v(t1).
Oeps.
Opinion is the medium between knowledge and ignorance (Plato)


Heb vorig jaar het examen wiskunde gehaald op TL niveau, maar wil naast mijn mbo over een jaartje mijzelf ook graag aanmelden voor het staatsexamen wiskunde B op havo niveau om mijzelf voor te bereiden op het hbo. Wat zijn goede wiskunde boeken voor zelf studie?
Dé keizer van FOK!, en koning van de klaagbaak. Dus negeer HCFeestbeest maar.


Weet iemand hoe ik de volgende formule in de vorm van L =... kan schrijven? Ik zit een beetje te knoeien omdat ik niet weet hoe ik van die LN afkom (logaritme).
Het gaat om de volgende vraag:
Ik moet dus allereerst de de winstformule opstellen, dus ik had:
Winst = P * O Ln L - N*W
Waarbij O die constante is (waarvan ik de naam niet ken), N het aantal werknemers, P de prijs van het product en W de Wage.
Nu komt het N = L en ik moet dus achter L =... komen om het daarin in te vullen. Vervolgens moet ik de winst afleiden naar L (volgens mij). Uiteindelijk moet ik uitkomen op:
[ Bericht 49% gewijzigd door Sucuk op 06-01-2016 16:11:14 ]
Het gaat om de volgende vraag:
Ik moet dus allereerst de de winstformule opstellen, dus ik had:
Winst = P * O Ln L - N*W
Waarbij O die constante is (waarvan ik de naam niet ken), N het aantal werknemers, P de prijs van het product en W de Wage.
Nu komt het N = L en ik moet dus achter L =... komen om het daarin in te vullen. Vervolgens moet ik de winst afleiden naar L (volgens mij). Uiteindelijk moet ik uitkomen op:
[ Bericht 49% gewijzigd door Sucuk op 06-01-2016 16:11:14 ]


Dan begrijp je niet wat een logaritme is.quote:Op woensdag 6 januari 2016 16:02 schreef Sucuk het volgende:
Weet iemand hoe ik de volgende formule in de vorm van L =... kan schrijven? Ik zit een beetje te knoeien omdat ik niet weet hoe ik van die LN afkom (logaritme).
[ afbeelding ]
We hebben
en ln L is per definitie de exponent waartoe je e moet verheffen om L te krijgen, dus?


e^ Q/O = Lquote:Op woensdag 6 januari 2016 16:12 schreef Riparius het volgende:
[..]
Dan begrijp je niet wat een logaritme is.
We hebben
en ln L is per definitie de exponent waartoe je e moet verheffen om L te krijgen, dus?
Weet alleen niet of het van belang is om de vraag te beantwoorden? (Zie edit. voorgaande post)


De letter θ heet theta en is een Griekse letter. Leer het Griekse alfabet en gebruik niet de Latijnse hoofdletter O als je een Griekse θ bedoelt.quote:Op woensdag 6 januari 2016 16:14 schreef Sucuk het volgende:
[..]
e^ Q/O = L
Weet alleen niet of het van belang is om de vraag te beantwoorden? (Zie edit. voorgaande post)


Thanks. Heb jij een idee hoe ik de vraag zou moeten oplossen?quote:Op woensdag 6 januari 2016 16:19 schreef Riparius het volgende:
[..]
De letter θ heet theta en is een Griekse letter. Leer het Griekse alfabet en gebruik niet de Latijnse hoofdletter O als je een Griekse θ bedoelt.


Basis algebra.quote:Op woensdag 6 januari 2016 16:21 schreef Sucuk het volgende:
[..]
Thanks. Heb jij een idee hoe ik de vraag zou moeten oplossen?
Je hebt Q = θ ln L =>
ln L = Q/θ
Substitueer dat in je andere formule.
En dan krijg je
winst = P Q - N W.
Maar daar heb je vast niet zoveel aan.
-edit- nu gebruik je L en N in dezelfde formule en die betekenen hetzelfde. Los het verder zelf maar op.
[ Bericht 7% gewijzigd door t4rt4rus op 06-01-2016 16:34:20 ]


Tuurlijk wel, ik moet dan toch die winst =... afleiden naar N (ofwel L)?quote:Op woensdag 6 januari 2016 16:26 schreef t4rt4rus het volgende:
[..]
Basis algebra.
Je hebt Q = θ ln L =>
ln L = Q/θ
Substitueer dat in je andere formule.
En dan krijg je
winst = P Q - N W.
Maar daar heb je vast niet zoveel aan.


Je moet bepalen voor welke waarde van L de uitdrukkingquote:Op woensdag 6 januari 2016 16:21 schreef Sucuk het volgende:
[..]
Thanks. Heb jij een idee hoe ik de vraag zou moeten oplossen?
voor de winst een maximum aanneemt, en dat doe je door deze uitdrukking naar L te differentiëren en de aldus verkregen afgeleide gelijk te stellen aan nul en dan daaruit L op te lossen.


Heb je opdracht ook maar even gelezen. Je moet eerst de winst afleiden naar L.quote:Op woensdag 6 januari 2016 16:31 schreef Sucuk het volgende:
[..]
Tuurlijk wel, ik moet dan toch die winst =... afleiden naar N (ofwel L)?
Weet je hoe je moet differentiëren?


quote:Op woensdag 6 januari 2016 16:32 schreef Riparius het volgende:
[..]
Je moet bepalen voor welke waarde van L de uitdrukking
voor de winst een maximum aanneemt, en dat doe je door deze uitdrukking naar L te differentiëren en de aldus verkregen afgeleide gelijk te stellen aan nul en dan daaruit L op te lossen.
Het is gelukt! Dankje!quote:Op woensdag 6 januari 2016 16:40 schreef t4rt4rus het volgende:
[..]
Heb je opdracht ook maar even gelezen. Je moet eerst de winst afleiden naar L.
Weet je hoe je moet differentiëren?


Bedenk wel dat het nul zijn van de eerste afgeleide geen voldoende voorwaarde is voor het optreden van een maximum (je zou immers ook nog een minimum of een buigpunt met een horizontale buigraaklijn kunnen hebben). Daarom moet je ook nog laten zien dat de tweede afgeleide naar L van de uitdrukking voor de winst negatief is voor de gevonden waarde van L.quote:


Thanks. Het is exact de volgende methodiek toch:quote:Op woensdag 6 januari 2016 17:00 schreef Riparius het volgende:
[..]
Bedenk wel dat het nul zijn van de eerste afgeleide geen voldoende voorwaarde is voor het optreden van een maximum (je zou immers ook nog een minimum of een buigpunt met een horizontale buigraaklijn kunnen hebben). Daarom moet je ook nog laten zien dat de tweede afgeleide naar L van de uitdrukking voor de winst negatief is voor de gevonden waarde van L.
Tweede afgeleide en vervolgens de tekentoets?


Dan haal je mogelijk twee zaken door elkaar. Het is nodig en voldoende om te kijken naar hetzij het tekenverloop van de eerste afgeleide hetzij het teken van de tweede afgeleide voor de gevonden waarde van L.quote:Op woensdag 6 januari 2016 17:03 schreef Sucuk het volgende:
[..]
Thanks. Het is exact de volgende methodiek toch:
Tweede afgeleide en vervolgens de tekentoets?


Ik weet niet of je er nog bent maar je moet even goed op je notatie letten.quote:Op dinsdag 5 januari 2016 16:57 schreef obsama het volgende:
[..]
Ja sorry wat te snel verwoord. Wat ik bedoel is het volgende:
Als ik de integraal tussen t1=0 en t2=5 neem van v(x) en de eenheid is meter per seconde dan is de uitkomst toch gewoon de afstand die ik heb afgelegd tussen t1 en t2 in meters per seconde?
Wat nou als ik de integraal neem van t1=0 en t2=5 van a(x), wat stelt het getal dat daar uitkomt dan voor?
Sorry voor het houtje touwtje bericht, ik hoop dat het zo iets duidelijker is.
Stel de positie op tijdstip t is
De snelheid op tijdstip t is gegeven door
En de acceleratie
Neem je het integraal van de acceleratie over het interval [t1, t2] dan krijgen we
Wat gelijk is aan het verschil van de snelheden op tijdstip t1 en t2.
Neem je het integraal van de snelheid dan krijg je het verschil van de posities op tijdstip t1 en t2.


quote:Op woensdag 6 januari 2016 15:15 schreef Bierpens. het volgende:
Heb vorig jaar het examen wiskunde gehaald op TL niveau, maar wil naast mijn mbo over een jaartje mijzelf ook graag aanmelden voor het staatsexamen wiskunde B op havo niveau om mijzelf voor te bereiden op het hbo. Wat zijn goede wiskunde boeken voor zelf studie?
Dé keizer van FOK!, en koning van de klaagbaak. Dus negeer HCFeestbeest maar.


Ik zou eerst een bijlesleraar zoeken, behalve als je zeker weet dat je een autodidact bent, dan kun je gewoon 'Getal en Ruimte' (voor havo bovenbouw wiskunde b) gebruiken. Volgens mij zijn dat 3 á 4 boeken...quote:
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Hallo,
Ik heb een vraag omtrent de toepassing van wiskunde in de volgende twee opgaven. Aangezien ik er nauwelijks uit kan komen, snap ik ook niet echt wat ik moet doen en hoe. Hopelijk kan iemand mij hierbij helpen:
Opgaven:
Ik heb een vraag omtrent de toepassing van wiskunde in de volgende twee opgaven. Aangezien ik er nauwelijks uit kan komen, snap ik ook niet echt wat ik moet doen en hoe. Hopelijk kan iemand mij hierbij helpen:
Opgaven:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Antwoorden van de opgaven:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Theorie omtrent de opgaven:
theorie voor opgave 2.3SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.theorie voor opgave 2.4SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
 quote:
quote:Op dinsdag 12 januari 2016 17:19 schreef Frank_Underwood het volgende:
Hallo,
Ik heb een vraag omtrent de toepassing van wiskunde in de volgende twee opgaven. Aangezien ik er nauwelijks uit kan komen, snap ik ook niet echt wat ik moet doen en hoe. Hopelijk kan iemand mij hierbij helpen:
Opgaven:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Antwoorden van de opgaven:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Theorie omtrent de opgaven:
theorie voor opgave 2.3SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.theorie voor opgave 2.4En je vraag is?SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Zo te zien is het economie.
Als je met concrete wiskunde vragen komt, kunnen we je vast helpen.
 Goedendag, een vraag voor jullie -
Goedendag, een vraag voor jullie -
Gegeven een topologische Hausdorff ruimte, en een compacte deelruimte A. Bewijs dat het quotiënt X/A met de bijbehorende quotiëntstopologie de Hausdorff eigenschap bezit, waarin X/A de ineenstorting van de deelruimte A op een punt is (wat is de juiste nederlandse vertaling van deze operatie?)
Ik weet dat A compact is in een Hausdorff ruimte, en daarom gesloten. Maar wat kan ik met deze wetenschap?Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
 Gegeven P en Q in X/A moet je dus bewijzen dat er open delen U en V om P en Q zijn die elkaar niet snijden. Je moet nu twee gevallen onderscheiden: P en Q zijn beide niet A, of een van de twee is A.quote:
Gegeven P en Q in X/A moet je dus bewijzen dat er open delen U en V om P en Q zijn die elkaar niet snijden. Je moet nu twee gevallen onderscheiden: P en Q zijn beide niet A, of een van de twee is A.quote:Op dinsdag 12 januari 2016 22:58 schreef Diacetylmorfine het volgende:
Goedendag, een vraag voor jullie -
Gegeven een topologische Hausdorff ruimte, en een compacte deelruimte A. Bewijs dat het quotiënt X/A met de bijbehorende quotiëntstopologie de Hausdorff eigenschap bezit, waarin X/A de ineenstorting van de deelruimte A op een punt is (wat is de juiste nederlandse vertaling van deze operatie?)
Ik weet dat A compact is in een Hausdorff ruimte, en daarom gesloten. Maar wat kan ik met deze wetenschap?
 Als P, Q beiden elementen uit X-A zijn is de vraag triviaal. Die zie ik!quote:
Als P, Q beiden elementen uit X-A zijn is de vraag triviaal. Die zie ik!quote:Op woensdag 13 januari 2016 06:48 schreef thabit het volgende:
[..]
Gegeven P en Q in X/A moet je dus bewijzen dat er open delen U en V om P en Q zijn die elkaar niet snijden. Je moet nu twee gevallen onderscheiden: P en Q zijn beide niet A, of een van de twee is A.
Ik weet dat alle elementen uit A op één element in A afgebeeld worden door de quotiëntsfunctie, en dat A een deelruimte van een Hausdorff ruimte is en daarmee de Hausdorff eigenschap erft. Dus voor alle P in X en Q in A bestaan deze U en V, en daarmee ook voor ieder punt waarop A mogelijk afgebeeld wordt. Maar dan heb ik geen gebruik gemaakt van de compactheid van A, wat mij doet vermoeden dat er iets niet klopt.Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet
 P in X-A en Q in A kun je open delen U en V vinden. Maar die V beeldt daarmee nog niet op een open deel in X/A af. Je moet de compactheid gebruiken om open delen in X te vinden die ook naar open delen in X/A afbeelden.quote:
P in X-A en Q in A kun je open delen U en V vinden. Maar die V beeldt daarmee nog niet op een open deel in X/A af. Je moet de compactheid gebruiken om open delen in X te vinden die ook naar open delen in X/A afbeelden.quote:Op woensdag 13 januari 2016 15:28 schreef Diacetylmorfine het volgende:
[..]
Als P, Q beiden elementen uit X-A zijn is de vraag triviaal. Die zie ik!
Ik weet dat alle elementen uit A op één element in A afgebeeld worden door de quotiëntsfunctie, en dat A een deelruimte van een Hausdorff ruimte is en daarmee de Hausdorff eigenschap erft. Dus voor alle P in X en Q in A bestaan deze U en V, en daarmee ook voor ieder punt waarop A mogelijk afgebeeld wordt. Maar dan heb ik geen gebruik gemaakt van de compactheid van A, wat mij doet vermoeden dat er iets niet klopt.
 Hoe kun je het beste leren bewijzen? Ik doe nu het Wiskundige Structuren dictaat van de Universiteit Leiden, maar bij het bewijzen van de wetten van De Morgan liep ik al vast.
Hoe kun je het beste leren bewijzen? Ik doe nu het Wiskundige Structuren dictaat van de Universiteit Leiden, maar bij het bewijzen van de wetten van De Morgan liep ik al vast.Eerste bewijsopgave in het dictaat. Ik heb geen idee waar ik moet beginnen bij zoiets...

 Verzamelingen zijn gelijk als ze dezelfde elementen hebbenquote:
Verzamelingen zijn gelijk als ze dezelfde elementen hebbenquote:Op woensdag 13 januari 2016 22:18 schreef netchip het volgende:
Nu heb ik ook geen college, dus dat helpt ook al niet echt mee.
Dus laten zien dat elk element in de linkerzijde ook in de rechterzijde zit, en andersom
 Te bewijzen:quote:
Te bewijzen:quote:Op woensdag 13 januari 2016 22:25 schreef Anoonumos het volgende:
[..]
Verzamelingen zijn gelijk als ze dezelfde elementen hebben
Dus laten zien dat elk element in de linkerzijde ook in de rechterzijde zit, en andersom
Dan moet gelden dateen deelverzameling is van
, en andersom. Dit had ik al bedacht. Ik nam aan dat er een x is in A en B, zodat x een element is van de doorsnede van A en B. Omdat dit element niet in zowel Ac als Bc zit, zal deze ook niet in de vereniging van deze verzamelingen zitten.
Ergens gaat er hier iets mis en mis ik wat. Welk geval ben ik vergeten?
 Uh omdat linksquote:
Uh omdat linksquote:Op woensdag 13 januari 2016 22:33 schreef netchip het volgende:
[..]
Te bewijzen:
Dan moet gelden dateen deelverzameling is van
, en andersom. Dit had ik al bedacht. Ik nam aan dat er een x is in A en B, zodat x een element is van de doorsnede van A en B. Omdat dit element niet in zowel Ac als Bc zit, zal deze ook niet in de vereniging van deze verzamelingen zitten.
Ergens gaat er hier iets mis en mis ik wat. Welk geval ben ik vergeten?is en niet
?

 Uhu maar als x inquote:
Uhu maar als x inquote:zit, dan zit deze niet in
. Dus dan kunnen we toch concluderen dat x geen element is van de linkerzijde, en niet van de rechterzijde?

 Ja het klopt wel, maar je schiet er niet veel mee op.quote:
Ja het klopt wel, maar je schiet er niet veel mee op.quote:Op woensdag 13 januari 2016 22:48 schreef netchip het volgende:
[..]
Uhu maar als x inzit, dan zit deze niet in
. Dus dan kunnen we toch concluderen dat x geen element is van de linkerzijde, en niet van de rechterzijde?
Je wilde laten dateen deelverzameling is van
dus neem x in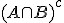

 Ik ga er morgen met pen en papier nog een keer goed voor zitten. Alvast bedankt!quote:
Ik ga er morgen met pen en papier nog een keer goed voor zitten. Alvast bedankt!quote:Op woensdag 13 januari 2016 16:16 schreef thabit het volgende:
[..]
P in X-A en Q in A kun je open delen U en V vinden. Maar die V beeldt daarmee nog niet op een open deel in X/A af. Je moet de compactheid gebruiken om open delen in X te vinden die ook naar open delen in X/A afbeelden.Oefenen. Heel veel. En voordat je begint aan een bewijs zorgen dat je een goed begrip hebt van de definities en stellingen die je tot je beschikking hebt, maar bovenal een goed beeld van wát je wil bewijzen. Als je er niet uit komt noteren wat je weet, of je afvragen wat er mis zou gaan als je stelling niet zou kloppen. Verder niet opgeven voor je het gevoel hebt dat je je bronnen uitgeput hebt.quote:Op woensdag 13 januari 2016 22:17 schreef netchip het volgende:
Hoe kun je het beste leren bewijzen? Ik doe nu het Wiskundige Structuren dictaat van de Universiteit Leiden, maar bij het bewijzen van de wetten van De Morgan liep ik al vast.Eerste bewijsopgave in het dictaat. Ik heb geen idee waar ik moet beginnen bij zoiets...
Cuius rei demonstrationem mirabilem sane detexi hanc marginis exiguitas non caparet

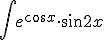
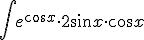
substitueer,
En dan zou ik integration by parts gebruiken, maar nou moet je dit doen:,
En dan pas integration by parts.
Hoe moet ik nou weten wanneer je dit soort trucjes moet toepassen?
http://www.wolframalpha.com/input/?i=integral+e^cosx+*+sin2x
 Doe het als volgt. Je hebtquote:
Doe het als volgt. Je hebtquote:
zodat
en aangezien
hebben we dus
Nu kunnen we gebruik maken van
met
en
zodat
en dus
Ik heb hier gebruik gemaakt van partiële integratie, maar ook van een impliciete substitutie. Als deze techniek je niet duidelijk is, bestudeer dan eens deze post van mij.
[ Bericht 0% gewijzigd door Riparius op 18-01-2016 14:51:43 ]
 Ik heb een vraag uit een oefententamen wiskunde waar ik met een klasgenoot samen maar niet uit kom, ik denk nu het goede antwoord gevonden te hebben. We hebben geen uitwerking en ook niet het antwoord van onze leraar gekregen vandaar dat ik het hier kom vragen. Dit is mijn uitwerking:
Ik heb een vraag uit een oefententamen wiskunde waar ik met een klasgenoot samen maar niet uit kom, ik denk nu het goede antwoord gevonden te hebben. We hebben geen uitwerking en ook niet het antwoord van onze leraar gekregen vandaar dat ik het hier kom vragen. Dit is mijn uitwerking:
Het is de bedoeling om de optimale afmetingen van de doos te vinden waarbij de totale materiaalkosten minimaal zijn.
[ Bericht 16% gewijzigd door Boarderzip op 19-01-2016 15:15:28 (Foutje in uitwerking) ]
 Post eens een foto van de originele opgave. Heeft de doos geen deksel?quote:
Post eens een foto van de originele opgave. Heeft de doos geen deksel?quote:Op dinsdag 19 januari 2016 14:47 schreef Boarderzip het volgende:
Ik heb een vraag uit een oefententamen wiskunde waar ik met een klasgenoot samen maar niet uit kom, ik denk nu het goede antwoord gevonden te hebben. We hebben geen uitwerking en ook niet het antwoord van onze leraar gekregen vandaar dat ik het hier kom vragen. Dit is mijn uitwerking:
[ afbeelding ]
Het is de bedoeling om de optimale afmetingen van de doos te vinden waarbij de totale materiaalkosten minimaal zijn.
 De doos heeft geen deksel, hierbij de opgave:quote:
De doos heeft geen deksel, hierbij de opgave:quote:Op dinsdag 19 januari 2016 15:31 schreef Riparius het volgende:
[..]
Post eens een foto van de originele opgave. Heeft de doos geen deksel?
De afmetingen van de doos zijn dus volgens mij 4,05 dm lang, 4,05 dm breed en 3,04 dm hoog.
 Je uitwerking lijkt me correct. Je moet alleen nog laten zien dat je kostenfunctie K(x) voor x ≈ 4,05 inderdaad een minimum aanneemt. Waarom twijfel je?quote:
Je uitwerking lijkt me correct. Je moet alleen nog laten zien dat je kostenfunctie K(x) voor x ≈ 4,05 inderdaad een minimum aanneemt. Waarom twijfel je?quote:Op dinsdag 19 januari 2016 15:35 schreef Boarderzip het volgende:
[..]
De doos heeft geen deksel, hierbij de opgave:
[ afbeelding ]
De afmetingen van de doos zijn dus volgens mij 4,05 dm lang, 4,05 dm breed en 3,04 dm hoog.
 Ik twijfel omdat ik geen controle mogelijkheid heb, geen van mijn klasgenoten kwam eruit. De afgelopen 2 dagen ben ik ook 5x opnieuw begonnen dus vandaar. Bedankt voor je antwoord, ik ben blij dat het gelukt is, op naar het tentamen morgenquote:
Ik twijfel omdat ik geen controle mogelijkheid heb, geen van mijn klasgenoten kwam eruit. De afgelopen 2 dagen ben ik ook 5x opnieuw begonnen dus vandaar. Bedankt voor je antwoord, ik ben blij dat het gelukt is, op naar het tentamen morgenquote:Op dinsdag 19 januari 2016 15:41 schreef Riparius het volgende:
[..]
Je uitwerking lijkt me correct. Je moet alleen nog laten zien dat je kostenfunctie K(x) voor x ≈ 4,05 inderdaad een minimum aanneemt. Waarom twijfel je?

 Ik had al een eigen topic gemaakt, maar volgens mij hoort de volgende vraag hier:
Ik had al een eigen topic gemaakt, maar volgens mij hoort de volgende vraag hier:
Hallo,
Ik heb een vraag over een kansberekening, ik hoop dat jullie me er bij kunnen helpen. Stel je hebt een pot met 100 knikkers. Eén ervan is geel. Elke dag pak je 10 knikkers uit de pot. Hoe groot is dan de kans dat de gele knikker na zes dagen nog in de pot zit? Ik kwam tot hier:
Dag 1 = kans van 0.1 dat de gele knikker gepakt wordt. 90 knikkers over.
Dag 2 = kans van 0.11 dat de gele knikker gepakt wordt. 80 knikkers over
Dag 3 = kans van 0.13 dat de gele knikker gepakt wordt. 70 knikkers over.
Dag 4 = kans van 0.15 dat de gele knikker gepakt wordt. 60 knikkers over.
Dag 5 = kans van 0.17 dat de gele knikker gepakt wordt. 50 knikkers over.
Dag 6 = kans van 0.2 dat de gele knikker gepakt wordt. 40 knikkers over.
Maar hoe tel ik vervolgens de kansen op, of vermenigvuldig ik ze, om er achter te komen wat de totale kans is dat de gele knikker na dag 6 nog in de pot zit?
Alvast bedankt!
 Volgens mij kan je het probleem beter bekijken als een pot met 99 (bijv.) rode knikkers en 1 gele knikker. Vervolgens pak je 60 knikkers zonder terugleggen. Wat is de kans dat de gele nog niet gepakt is?quote:
Volgens mij kan je het probleem beter bekijken als een pot met 99 (bijv.) rode knikkers en 1 gele knikker. Vervolgens pak je 60 knikkers zonder terugleggen. Wat is de kans dat de gele nog niet gepakt is?quote:Op woensdag 27 januari 2016 10:48 schreef Zwelgje84 het volgende:
Ik had al een eigen topic gemaakt, maar volgens mij hoort de volgende vraag hier:
Hallo,
Ik heb een vraag over een kansberekening, ik hoop dat jullie me er bij kunnen helpen. Stel je hebt een pot met 100 knikkers. Eén ervan is geel. Elke dag pak je 10 knikkers uit de pot. Hoe groot is dan de kans dat de gele knikker na zes dagen nog in de pot zit? Ik kwam tot hier:
Dag 1 = kans van 0.1 dat de gele knikker gepakt wordt. 90 knikkers over.
Dag 2 = kans van 0.11 dat de gele knikker gepakt wordt. 80 knikkers over
Dag 3 = kans van 0.13 dat de gele knikker gepakt wordt. 70 knikkers over.
Dag 4 = kans van 0.15 dat de gele knikker gepakt wordt. 60 knikkers over.
Dag 5 = kans van 0.17 dat de gele knikker gepakt wordt. 50 knikkers over.
Dag 6 = kans van 0.2 dat de gele knikker gepakt wordt. 40 knikkers over.
Maar hoe tel ik vervolgens de kansen op, of vermenigvuldig ik ze, om er achter te komen wat de totale kans is dat de gele knikker na dag 6 nog in de pot zit?
Alvast bedankt!
Volgens mij (kansrekenen is alweer een beetje weggezakt) is de kans dan 99/100 * 98/99 etc. Dit kan je ook handiger schrijven met faculteiten enzo, maar geen idee hoe dat ook alweer moet.leef de leven
 Het is vast triviaal, maar ik zie het niet...
Het is vast triviaal, maar ik zie het niet...
In dit linkje, onder vergelijking (1), wordt er gezegd "A normal vector to this surface is given by...".
Hoe zie ik dit in?
Met loodrecht op de grafiek wordt denk ik bedoeld loodrecht op (x,y,z(x,y)). Dus het inproduct daarmee zou 0 moeten zijn. Maar dat snap ik niet.
 Een vergelijking voor het raakvlak aan (a, b, f(a,b)) isquote:
Een vergelijking voor het raakvlak aan (a, b, f(a,b)) isquote:Op donderdag 28 januari 2016 18:00 schreef thenxero het volgende:
Het is vast triviaal, maar ik zie het niet...
In dit linkje, onder vergelijking (1), wordt er gezegd "A normal vector to this surface is given by...".
Hoe zie ik dit in?
Met loodrecht op de grafiek wordt denk ik bedoeld loodrecht op (x,y,z(x,y)). Dus het inproduct daarmee zou 0 moeten zijn. Maar dat snap ik niet.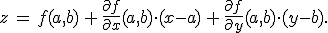

 Haha, ik zie het al. Bedankt.quote:
Haha, ik zie het al. Bedankt.quote:Op donderdag 28 januari 2016 18:10 schreef thabit het volgende:
[..]
Een vergelijking voor het raakvlak aan (a, b, f(a,b)) is
 Hoe bepaald je bij een multivariate functie of hij continue is?
Hoe bepaald je bij een multivariate functie of hij continue is?
voorbeeld:
f(x,y) = abs(xy)
Ik heb vroeger wel geleerd hoe je kan controleren of een functie continue is op een bepaald punt door vanaf beide zijden dat punt te benaderen en dan zou je op hetzelfde antwoord moeten uitkomen.
Alleen hoe bewijs ik dit voor een gehele functie? En vooral hoe bewijs ik dit met meerdere variabelen?
 Hii, wij zijn nu op school bij het hoofdstuk verbanden. nu moet ik nog een aantal opdrachten afronden voor morgen.. :blush:
Hii, wij zijn nu op school bij het hoofdstuk verbanden. nu moet ik nog een aantal opdrachten afronden voor morgen.. :blush:
Ik loop bij een vraagje steeds vast en dat is bij onderstaande vraag :
Bij een bloedproef bleek er bij iemand 1,5 promille alcohol in zijn bloed te zitten.
Met de formule kun je uitrekenen hoeveel promille alcohol er na een aantal uren nog in zijn bloed zit.
Hoeveel is dat na 4 uur? Rond je antwoord af op 2 decimalen.
De formule is : R=S X0,5 (0,2Xt)
R = rest
S = starthoeveelheid
T = tijd in uren nu staat die (0,2xt) iets boven de 0,5.. ik heb geen idee hoe ik dit moet uitrekenen
is er iemand die mij kan helpen?
Liefs, xox
Bewerk bericht
 Dat is een exponentquote:
Dat is een exponentquote:Op woensdag 3 februari 2016 14:00 schreef elena1997 het volgende:
nu staat die (0,2xt) iets boven de 0,5.. ik heb geen idee hoe ik dit moet uitrekenen
0.5 ^ (0.2 * t) invullen op je rekenmachine
 Voor de stelling dat er getallen a,b in N zijn met b ≠ 0 en q,r in N zodat a = qb+r en bovendien 0 ≤ r < b, wordt het volgende bewijs gegeven:
Voor de stelling dat er getallen a,b in N zijn met b ≠ 0 en q,r in N zodat a = qb+r en bovendien 0 ≤ r < b, wordt het volgende bewijs gegeven:
De verzameling S = { a, a-b, a-2b, a-3b, ... } heeft een kleinste natuurlijk getal in zich, namelijk r = a-qb voor een zekere q. Dan geldt r-b < 0 dus r = b.
Maar stel nu dat het kleinste natuurlijke getal in S 0 is, dan trek je een natuurlijk getal b > 0 ervan af, en dan krijg je dus een getal kleiner dan 0. Hoe zit dit?
[ Bericht 0% gewijzigd door netchip op 14-02-2016 13:50:41 ]
 Je bedoelt neem ik aan r < b ipv r = b.quote:
Je bedoelt neem ik aan r < b ipv r = b.quote:Op zondag 14 februari 2016 13:42 schreef netchip het volgende:
Voor de stelling dat er getallen a,b in N zijn met b ≠ 0 en q,r in N zodat a = qb+r en bovendien 0 ≤ r < b, wordt het volgende bewijs gegeven:
De verzameling S = { a, a-b, a-2b, a-3b, ... } heeft een kleinste natuurlijk getal in zich, namelijk r = a-qb voor een zekere q. Dan geldt r-b < 0 dus r = b.In dat geval is r dus 0.quote:Maar stel nu dat het kleinste natuurlijke getal in S 0 is, dan trek je een natuurlijk getal b > 0 ervan af, en dan krijg je dus een getal kleiner dan 0. Hoe zit dit?
 Ik bedoelde inderdaad r < b.quote:
Ik bedoelde inderdaad r < b.quote:Op zondag 14 februari 2016 14:24 schreef thabit het volgende:
[..]
Je bedoelt neem ik aan r < b ipv r = b.
[..]
In dat geval is r dus 0.
Maar stel a = 11 en b = 2, dan krijg je S = { 11, 9, 7, 5, 3, 1, -1, ... }. r is hier dan dus 1. Maar r - b = -1 en dus niet groter dan 0...
Laat maar, heb het teken verkeerd gelezen...
 Klopt, het is kleiner dan 0, en dat moet ook: je wilt r < b, dus r-b < 0.quote:
Klopt, het is kleiner dan 0, en dat moet ook: je wilt r < b, dus r-b < 0.quote:Op zondag 14 februari 2016 14:46 schreef netchip het volgende:
[..]
Ik bedoelde inderdaad r < b.
Maar stel a = 11 en b = 2, dan krijg je S = { 11, 9, 7, 5, 3, 1, -1, ... }. r is hier dan dus 1. Maar r - b = -1 en dus niet groter dan 0...
 Hallo, ik had een vraag over de algebraïsche manipulatie die ze in deze twee opgaven toepassen. Het betreft het uitwerken van differentialen/afgeleiden van matrix/vector-functies (Fréchet-afgeleide).
Hallo, ik had een vraag over de algebraïsche manipulatie die ze in deze twee opgaven toepassen. Het betreft het uitwerken van differentialen/afgeleiden van matrix/vector-functies (Fréchet-afgeleide).
Het accent ' wordt gebruikt om de getransponeerde aan te geven.
Ik heb de stappen die ik niet begrijp met een rode lijn aangegeven. Ze draaien hier opeens de volgorde van de multiplicatie om of iets dergelijks (35b)? En sommige van de elementen worden opeens getransponeerd (35b). Ik heb een beetje het idee alsof ik wat algebraische regels mbt multiplicatie van matrices, vectoren en hun getransponeerden mis.
Ik weet uiteraard wel wat een getransponeerde inhoudt, wat de basic rekenregels zijn (de volgorde van multiplicatie is belangrijk) en dat bijvoorbeeld
maar ik kan niet verklaren waarom de vector b opeens getransponeerd is en vooraan de multiplicatie staat (vraag 35b).
Wat betreft opgave 38, ze gebruiken hier waarschijnlijk de productregel. Wat mij betreft zou hier uitkomen x'dx+ dx'x en niet 2x'dx
Ik hoop dat iemand mij kan helpen! Bij voorbaat dank!
[ Bericht 0% gewijzigd door ulq op 14-02-2016 18:51:33 ]
 Goedemiddag,
Goedemiddag,
Weet iemand hoe ik de welvaartswinst (efficiencygain) van de volgende vraag kan berekenen?
Een paar vaste gegevens:
Prijs: 180
Belasting: 50
Q zonder belasting: 100
Q met belasting (sociaal optimum): 150
MC = 30 + Q
MC sociaal optimum = MC + MEC
MC sociaal optimum: 30 + Q + (1/2)Q
MC sociaal optimum: 30 + (3/2)Q
[b]Alvast enorm bedankt!!!
[/b]
Zelf heb ik tot nu toe:
(1/2) * (150-100) * xxx
Ik moet dus iets bij de xxx invullen, maar ik weet niet wat
P.s; ik studeer aan de UvA, misschien dat er ook mensen aan deze onderwijsinstelling studeren?

 Zo te zien ectrie @ eur, over dat x'dx+ dx'x & 35b staan uitgelegd in de slides van deze week!quote:
Zo te zien ectrie @ eur, over dat x'dx+ dx'x & 35b staan uitgelegd in de slides van deze week!quote:Op zondag 14 februari 2016 18:44 schreef ulq het volgende:
Hallo, ik had een vraag over de algebraïsche manipulatie die ze in deze twee opgaven toepassen. Het betreft het uitwerken van differentialen/afgeleiden van matrix/vector-functies (Fréchet-afgeleide).
Het accent ' wordt gebruikt om de getransponeerde aan te geven.
Ik heb de stappen die ik niet begrijp met een rode lijn aangegeven. Ze draaien hier opeens de volgorde van de multiplicatie om of iets dergelijks (35b)? En sommige van de elementen worden opeens getransponeerd (35b). Ik heb een beetje het idee alsof ik wat algebraische regels mbt multiplicatie van matrices, vectoren en hun getransponeerden mis.
[ afbeelding ]
Ik weet uiteraard wel wat een getransponeerde inhoudt, wat de basic rekenregels zijn (de volgorde van multiplicatie is belangrijk) en dat bijvoorbeeld
[ afbeelding ]
maar ik kan niet verklaren waarom de vector b opeens getransponeerd is en vooraan de multiplicatie staat (vraag 35b).
Wat betreft opgave 38, ze gebruiken hier waarschijnlijk de productregel. Wat mij betreft zou hier uitkomen x'dx+ dx'x en niet 2x'dx
Ik hoop dat iemand mij kan helpen! Bij voorbaat dank!
 Ze gebruiken daar dat een scalar z'n eigen getransponeerde is. Dus die tweede term isquote:
Ze gebruiken daar dat een scalar z'n eigen getransponeerde is. Dus die tweede term isquote:Op zondag 14 februari 2016 18:44 schreef ulq het volgende:
Hallo, ik had een vraag over de algebraïsche manipulatie die ze in deze twee opgaven toepassen. Het betreft het uitwerken van differentialen/afgeleiden van matrix/vector-functies (Fréchet-afgeleide).
Het accent ' wordt gebruikt om de getransponeerde aan te geven.
Ik heb de stappen die ik niet begrijp met een rode lijn aangegeven. Ze draaien hier opeens de volgorde van de multiplicatie om of iets dergelijks (35b)? En sommige van de elementen worden opeens getransponeerd (35b). Ik heb een beetje het idee alsof ik wat algebraische regels mbt multiplicatie van matrices, vectoren en hun getransponeerden mis.
[ afbeelding ]
Ik weet uiteraard wel wat een getransponeerde inhoudt, wat de basic rekenregels zijn (de volgorde van multiplicatie is belangrijk) en dat bijvoorbeeld
[ afbeelding ]
maar ik kan niet verklaren waarom de vector b opeens getransponeerd is en vooraan de multiplicatie staat (vraag 35b).
Wat betreft opgave 38, ze gebruiken hier waarschijnlijk de productregel. Wat mij betreft zou hier uitkomen x'dx+ dx'x en niet 2x'dx
Ik hoop dat iemand mij kan helpen! Bij voorbaat dank!
a'X(dX)'b = (a'X(dX)'b)' = b'(dX)X'a.
 Ja, ze werden beiden gelukkig besproken.quote:
Ja, ze werden beiden gelukkig besproken.quote:Op maandag 15 februari 2016 22:35 schreef stroomkoning het volgende:
[..]
Zo te zien ectrie @ eur, over dat x'dx+ dx'x & 35b staan uitgelegd in de slides van deze week!Het enige dingetje dat ik inderdaad miste (voor beide opgaven) was dat het beiden 1x1 matrices (scalairen) zijn die je dus gewoon kan transponeren. Dank voor de reactie in ieder geval.quote:Op maandag 15 februari 2016 22:59 schreef thabit het volgende:
[..]
Ze gebruiken daar dat een scalar z'n eigen getransponeerde is. Dus die tweede term is
a'X(dX)'b = (a'X(dX)'b)' = b'(dX)X'a.
 vierkant?quote:
vierkant?quote:Op dinsdag 16 februari 2016 12:44 schreef GeschiktX het volgende:
Klopt het dat de driehoek in dit vierkant 1/2 ruimte inneemt van de vierkant?
[ afbeelding ]
Maar het antwoord op je vraag is ja (mits rechte lijnen en zulks).Opinion is the medium between knowledge and ignorance (Plato)
 Het woord vierkant is onzijdig. En heb je nooit geleerd dat de oppervlakte van een driehoek gelijk is aan de helft van het product van de basis en de hoogte van de driehoek?quote:
Het woord vierkant is onzijdig. En heb je nooit geleerd dat de oppervlakte van een driehoek gelijk is aan de helft van het product van de basis en de hoogte van de driehoek?quote:Op dinsdag 16 februari 2016 12:44 schreef GeschiktX het volgende:
Klopt het dat de driehoek in dit vierkant deze rechthoek 1/2 ruimte de helft van de oppervlakte inneemt van de vierkant de rechthoek?
 Deel de rechthoek in twee gelijke delen door horizontale lijn te trekken.quote:
Deel de rechthoek in twee gelijke delen door horizontale lijn te trekken.quote:Op dinsdag 16 februari 2016 12:44 schreef GeschiktX het volgende:
Klopt het dat de driehoek in dit vierkant 1/2 ruimte inneemt van de vierkant?
[ afbeelding ]
Dan moet het wel duidelijk zijn.
 Hoi allemaal,
Hoi allemaal,
Ik heb een stelling omtrent wiskunde A kansrekenen waar ik niet uitkom hoe ik deze kan berekenen om het vervolgens te beantwoorden met (on)juist:
Stel dat er twee types tweedehands auto’s zijn: goede en slechte. Er zijn
veel potentiële kopers en verkopers van tweedehands auto’s. Zowel kopers
als verkopers zijn risico-neutraal. Gedeelte x van alle tweedehands auto’s is
goed, het overige deel 1−x van de tweedehands auto’s is slecht. De verkoper
van een tweedehands auto weet of zijn auto goed of slecht is. Kopers van
tweedehands auto’s kunnen aan een auto niet zien of deze goed of slecht is.
Verkopers waarderen een goede auto op 3000 euro en een slechte auto op 500
euro. Kopers waarderen een goede auto op 4600 euro en een slechte auto op
600 euro.
Veronderstel dat als een auto verkocht wordt, de prijs gelijk is aan de verwachte
waardering van de koper.
Veronderstel nu dat er een test beschikbaar komt. De test zorgt er voor dat
kopers ook de kwaliteit van de auto leren (dus leren of de auto goed of slecht
is). De test kost 1000 euro.
stelling: Als x < 0,75, dan leidt de beschikbaarheid van de test tot hogere
efficiëntie.
Alvast bedankt..
 Bedankt voor je mededeling. Wat is nu je vraag?quote:
Bedankt voor je mededeling. Wat is nu je vraag?quote:Op woensdag 17 februari 2016 11:33 schreef Sucuk het volgende:
Hoi allemaal,
Ik heb een stelling omtrent wiskunde A kansrekenen waar ik niet uitkom hoe ik deze kan berekenen om het vervolgens te beantwoorden met (on)juist:
 De stelling is strikt genomen waar. Het complement geldt echter niet. Als x > 0,75 dan leidt dat niet in alle gevallen tot een hogere efficiëntie vanuit het kopersperspectief.quote:
De stelling is strikt genomen waar. Het complement geldt echter niet. Als x > 0,75 dan leidt dat niet in alle gevallen tot een hogere efficiëntie vanuit het kopersperspectief.quote:Op woensdag 17 februari 2016 11:33 schreef Sucuk het volgende:
stelling: Als x < 0,75, dan leidt de beschikbaarheid van de test tot hogere
efficiëntie.
Vaag verhaal, redelijke opgave, ik ga jouw huiswerk natuurlijk niet voor je doen.
[ Bericht 3% gewijzigd door Repelsteeltju op 17-02-2016 17:03:30 ]“An interesting thing is a good thing.”
 Dit is een vragentopic. Ik kom dus even ergens niet uit en ik zoek hulp.quote:
Dit is een vragentopic. Ik kom dus even ergens niet uit en ik zoek hulp.quote:Op woensdag 17 februari 2016 16:52 schreef Repelsteeltju het volgende:
[..]
De stelling is strikt genomen waar. Het complement geldt echter niet. Als x > 0,75 dan leidt dat niet in alle gevallen tot een hogere efficiëntie vanuit het kopersperspectief.
Vaag verhaal, redelijke opgave, ik ga jouw huiswerk natuurlijk niet voor je doen.
 Misschien helpt het dan ook om te vertellen waar je op vast loopt.quote:
Misschien helpt het dan ook om te vertellen waar je op vast loopt.quote:Op woensdag 17 februari 2016 17:29 schreef Sucuk het volgende:
[..]
Dit is een vragentopic. Ik kom dus even ergens niet uit en ik zoek hulp.“An interesting thing is a good thing.”
 quote:
quote:Op woensdag 17 februari 2016 16:02 schreef thabit het volgende:
[..]
Bedankt voor je mededeling. Wat is nu je vraag?quote:Op woensdag 17 februari 2016 17:32 schreef Repelsteeltju het volgende:
[..]
Misschien helpt het dan ook om te vertellen waar je op vast loopt.
Vraag 4 en 5, is identiek wat ik ook in mijn schrift heb staan, maar de gehele uitwerking van 6 snap ik dus niet.. Ik weet niet hoe ik erop kan komen en kan bewijzen dat alles onder de 0,6 kan leiden tot efficientiewinst en alles tussen de 0,6 en 0,75 kan leiden tot lagere efficientie..
 Hallo allemaal,
Hallo allemaal,
Ik loop vast met een opgave waarbij ik een extra term moet toevoegen in een functie, maar het gaat een klein beetje mis..
Het betreft vraag numero 30 van de opgave:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Bij vraag numero 29 moest ik een nutsfunctie opstellen waarbij de extra term nog aan de orde was en ik deed het volgende:
Nutsfunctie = W + B [(0,5 + Beta(e1 +e2)] + W(1 - [0,5 + Beta(e1 + e2)]) - 0,5e²
Voor B = W+ Z invullen en alles netjes uitschrijven resulteert tot:
Maar hoe doe ik dit met de extra term?
Antwoord moet zijn:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
 Hallo, ik had een korte vraag over deze definitie van elementen van matrices.
Hallo, ik had een korte vraag over deze definitie van elementen van matrices.
Ik snap niet helemaal wat hier bedoeld met de 'e'-termen, en dit wordt helaas nergens echt verduidelijkt. Het leek mij dat dit ''element'' of iets dergelijks betekent en niet het getal van Euler, maar dan nog snap ik de definitie niet. In het element wordt in dat geval alleen de rijaangegeven of de kolom (j)? Ik snap niet hoe uit deze matrixvermenigvuldiging een getal volgt wat gelijk is aan element A ij...

 e_i^T = (0,0,...,0,1,0,..,0) met 1 op plek iquote:
e_i^T = (0,0,...,0,1,0,..,0) met 1 op plek iquote:Op dinsdag 23 februari 2016 14:35 schreef ulq het volgende:
Hallo, ik had een korte vraag over deze definitie van elementen van matrices.
[ afbeelding ]
Ik snap niet helemaal wat hier bedoeld met de 'e'-termen, en dit wordt helaas nergens echt verduidelijkt. Het leek mij dat dit ''element'' of iets dergelijks betekent en niet het getal van Euler, maar dan nog snap ik de definitie niet. In het element wordt in dat geval alleen de rijaangegeven of de kolom (j)? Ik snap niet hoe uit deze matrixvermenigvuldiging een getal volgt wat gelijk is aan element A ij...

 De definitie van 'e' is een vector met alleen maar 0'en en één 1 op plek 'i'?quote:
De definitie van 'e' is een vector met alleen maar 0'en en één 1 op plek 'i'?quote:Op dinsdag 23 februari 2016 14:37 schreef Anoonumos het volgende:
[..]
e_i^T = (0,0,...,0,1,0,..,0) met 1 op plek i
[ Bericht 0% gewijzigd door ulq op 23-02-2016 14:52:10 ]
 Jaquote:
Jaquote:Op dinsdag 23 februari 2016 14:46 schreef ulq het volgende:
[..]
De definitie van 'e' is een vector met alleen maar 0'en en één 1 op plek 'i'?
Hier heeft e_i lengte m en e_j lengte n maar dat volgt uit de context.
 Ah oké dan begrijp ik em inderdaad. Iets simpeler dan ik gedacht hadquote:
Ah oké dan begrijp ik em inderdaad. Iets simpeler dan ik gedacht hadquote:Op dinsdag 23 februari 2016 14:55 schreef Anoonumos het volgende:
[..]
Ja
Hier heeft e_i lengte m en e_j lengte n maar dat volgt uit de context.
Thanks!
 Ik had nog een kort vraagje wel. Als het goed is is de uitkomst een matrix met een boel nullen en één getal, a_ij, ongelijk aan 0? Je wil toch eigenlijk dat a_ij een scalair is ipv een matrix?
Ik had nog een kort vraagje wel. Als het goed is is de uitkomst een matrix met een boel nullen en één getal, a_ij, ongelijk aan 0? Je wil toch eigenlijk dat a_ij een scalair is ipv een matrix?
edit: Laat maar, fout gezien.
 Kan iemand mij helpen
Kan iemand mij helpen
De laatste stap bij statement 1 (blauwe box) van:
3a = a(a2 + 3a +2) naar
a(a2 + 3a- 1)=0
Snap ik niet.
Overigens, voor de geïnteresseerde, het antwoord op de vraag isSPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
 Je trekt aan beide kanten 3a af. 2a - 3a = -1a, vandaar de -1 tussen de haakjes.
Je trekt aan beide kanten 3a af. 2a - 3a = -1a, vandaar de -1 tussen de haakjes.
Als je eerst de haakjes wegwerkt, dan de 3a aftrekt, dan weer a buiten haakjes haalt, dan zie je 't wel denk ik?Voegt hoogtepunten toe aan jullie druilerige bestaan.
 Het was ook wat logischer geweest als ze in de stap van de vierde naar de vijfde regel in die blauwe box eerst de 3a hadden afgetrokken en daarna pas de a buiten haakjes hadden gehaald.Voegt hoogtepunten toe aan jullie druilerige bestaan.
Het was ook wat logischer geweest als ze in de stap van de vierde naar de vijfde regel in die blauwe box eerst de 3a hadden afgetrokken en daarna pas de a buiten haakjes hadden gehaald.Voegt hoogtepunten toe aan jullie druilerige bestaan.
 ahh thanks, als je inderdaad de haakjes wegwerkt is het heel logisch.
ahh thanks, als je inderdaad de haakjes wegwerkt is het heel logisch.
Beetje raar dat ze dat dan niet deden voordat ze de formule in haakjes zette, het brengt zo extra verwarring.
 Ik voer een two-sample t-test uit op een dataset. Nu wil ik deze dataset corrigeren met Bonforroni FDR. Ik rangschik de p-waarden die uit de test komen van laag naar hoog. Die p-waarden moet ik keer het totaal aantal metingen doen en dan delen door hun rang, maar hoe doe ik dat laatste? Ik werk in Matlab.Gist is liefde, gist is leven. Vooral in een vagijn.
Ik voer een two-sample t-test uit op een dataset. Nu wil ik deze dataset corrigeren met Bonforroni FDR. Ik rangschik de p-waarden die uit de test komen van laag naar hoog. Die p-waarden moet ik keer het totaal aantal metingen doen en dan delen door hun rang, maar hoe doe ik dat laatste? Ik werk in Matlab.Gist is liefde, gist is leven. Vooral in een vagijn.
 Hier zitten de slimmere bollebozen dus wie kan mij helpen met de uitleg en het antwoord?
Hier zitten de slimmere bollebozen dus wie kan mij helpen met de uitleg en het antwoord?
5% van ...% van 22 is 11
Hij komt zo simpel over maar ik kom er gewoon niet uit


 quote:
quote:thanks, voel me zo dom dat ik er gewoon niet op kwam
terwijl ik het antwoord nu zie is het zo logisch

 Hoe bereken je ook alweer:
Hoe bereken je ook alweer:
Als je schrijft:
was het dan niet:
Maar ik ben de redenering even kwijt... Hoe zat het ook alweer?
En verandert er iets als A niet symmetrisch is?
Kon je niet een soort van ketting- en productregel toepassen?
 quote:
quote:Op maandag 21 maart 2016 10:25 schreef Epps. het volgende:
Goedemorgen,
ik heb de mogelijkheid om via de Erasmus universiteit een wiskunde deficientecursus te volgen en zodoende toch toegelaten te worden tot de opleiding die ik wil volgen.
De cursus kost enkele honderden euro's en ik vroeg me af of het haalbaar is om de getoetste stof in twee maanden tijd te beheersen.
Heb zelf geen wiskunde meer gehad sinds de onderbouw dus mijn basiskennis is bijna 0,0.
Hieronder een voorbeeldtoets:
http://www.eur.nl/fileadm(...)au_2_versie_2014.pdf
Ik hoop dat jullie me hierbij willen helpen, indien jullie nog verdere vragen hebben kunnen jullie die uiteraard stellen in dit topic.
 Als A niet symmetrisch is, dan geldt dat =-teken met het vraagteken erboven niet.quote:
Als A niet symmetrisch is, dan geldt dat =-teken met het vraagteken erboven niet.quote:Op maandag 21 maart 2016 01:45 schreef Hahatsjoe het volgende:
Hoe bereken je ook alweer:
Als je schrijft:
was het dan niet:
Maar ik ben de redenering even kwijt... Hoe zat het ook alweer?
En verandert er iets als A niet symmetrisch is?
Kon je niet een soort van ketting- en productregel toepassen?
 Echt niet? Want als ik het uitschrijf komt het er volgens mij gewoon uit. Het zijn uiteindelijk toch gewoon scalars en de volgorde waarin ik die vermenigvuldig dan wel optel maakt niet uit?quote:
Echt niet? Want als ik het uitschrijf komt het er volgens mij gewoon uit. Het zijn uiteindelijk toch gewoon scalars en de volgorde waarin ik die vermenigvuldig dan wel optel maakt niet uit?quote:Op maandag 21 maart 2016 13:04 schreef thabit het volgende:
[..]
Als A niet symmetrisch is, dan geldt dat =-teken met het vraagteken erboven niet.
 Voorbeeldje dan, waaruit blijkt dat je de symmetrie toch echt nodig hebt:
Voorbeeldje dan, waaruit blijkt dat je de symmetrie toch echt nodig hebt:
Dan ismet als afgeleide
.
, en
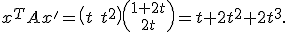

 Ohja. Zeer vriendelijk bedankt!quote:
Ohja. Zeer vriendelijk bedankt!quote:Op maandag 21 maart 2016 20:03 schreef thabit het volgende:
Voorbeeldje dan, waaruit blijkt dat je de symmetrie toch echt nodig hebt:
Dan ismet als afgeleide
.
, en

 Hallo, is er iemand die me verder zou willen helpen?
Hallo, is er iemand die me verder zou willen helpen?
Ik moet voor een verslag een "loglinear approximation" uitvoeren voor deze parabool rondom het punt gA*:
Nu heb ik de volgende stappen ondernomen waarbij ik op het juiste antwoord uitkom:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Ik heb alleen geen idee of mijn derivaties kloppen. Ook weet ik niet zeker of mijn vergelijkingen consistent zijn met deze grafiek, aangezien ik uitga van ggA en de grafiek van gA-punt. Zou er iemand zo vriendelijk willen zijn om te dubbel checken of dit inderdaad klopt?
 Bij de eerste som:
Bij de eerste som:
Waarom is de oplossing 1/2pi + kpi en niet 1/2pi +2kpi?
En waarom nemen ze (2x+1/4pi)=-1/2pi + 2kpi niet mee?
 Omdat cos(u) = 0 geldt voor u = (1/2)*pi + k*pi, waar k wordt gebruikt om veelvouden van pi aan te geven.quote:
Omdat cos(u) = 0 geldt voor u = (1/2)*pi + k*pi, waar k wordt gebruikt om veelvouden van pi aan te geven.quote:Op woensdag 30 maart 2016 12:08 schreef Goldenrush het volgende:
Waarom is de oplossing 1/2pi + kpi en niet 1/2pi +2kpi?
cos(u) = 0 geldt namelijk voor u=(1/2)*pi+pi, u=(1/2)*pi+2*pi, u=(1/2)*pi+3*pi, etc.
Kijk maar naar https://www.google.nl/sea(...)ceid=chrome&ie=UTF-8
Je kan voor k dus elke integer kiezen, niet enkel de even getallen: 2,4,6, etc.
[ Bericht 11% gewijzigd door ulq op 30-03-2016 15:35:15 ]
 Denk aan de eenheidscirkel: de cosinus van een rotatiehoek is per definitie de x-coördinaat van het beeldpunt van (1; 0) bij rotatie om de oorsprong over die hoek. Zie ook hier.quote:
Denk aan de eenheidscirkel: de cosinus van een rotatiehoek is per definitie de x-coördinaat van het beeldpunt van (1; 0) bij rotatie om de oorsprong over die hoek. Zie ook hier.quote:Op woensdag 30 maart 2016 12:08 schreef Goldenrush het volgende:
Bij de eerste som:
[ afbeelding ]
Waarom is de oplossing 1/2pi + kpi en niet 1/2pi +2kpi?
Welnu, als je het startpunt (1; 0) over ½π rad om de oorsprong roteert, dan kom je uit in het punt (0; 1) en de x-coördinaat van dat punt - en daarmee de cosinus van ½π - is dus inderdaad 0. Maar als je nu vervolgens nog over een geheel aantal halve slagen in tegenwijzerzin of in wijzerzin rond de oorsprong roteert, dan kom je óf weer uit op het punt (0;1) óf op het punt (0;−1) en ook dan is de x-coördinaat van het beeldpunt - en dus de cosinus - weer gelijk aan 0. Dus is
cos(2x + ¼π) = 0
equivalent met
2x + ¼π = ½π + kπ, k ∈ ℤDat zou ook kunnen, maar is hier minder handig. Je kunt bedenken dat de cosinus van ½π gelijk is aan nul, zodatquote:En waarom nemen ze (2x+1/4pi)=-1/2pi + 2kpi niet mee?
cos(2x + ¼π) = 0
equivalent is met
cos(2x + ¼π) = cos(½π)
Nu zijn de cosinussen van twee (rotatie)hoeken gelijk als die (rotatie)hoeken hetzij aan elkaar gelijk zijn, hetzij elkaars tegengestelde zijn, afgezien van een geheel veelvoud van 2π, dus
cos α = cos β ⇔ α = β + k·2π ∨ α = −β + k·2π, k ∈ ℤ
zodat
cos(2x + ¼π) = cos(½π)
dus equivalent is met
2x + ¼π = ½π + 2kπ ∨ 2x + ¼π = −½π + 2kπ, k ∈ ℤ
en dit geeft
x = ⅛π + kπ ∨ x = −⅜π + kπ, k ∈ ℤ
Maar nu kun je bedenken dat het verschil tussen een rotatie over (1/8)·π rad en een rotatie over (−3/8)·π rad een rotatie is over ½π rad, en dat is de helft van π rad, zodat we de beide deeloplossingen hier samen kunnen voegen en de volledige oplossing dus eenvoudiger kunnen schrijven als
x = ⅛π + k·½π, k ∈ ℤ
Dit is uiteraard precies hetzelfde resultaat, maar je ziet nu dat het handiger is om gelijk te bedenken dat een cosinus van een rotatiehoek gelijk is aan nul als die rotatiehoek gelijk is aan ½π rad plus een geheel veelvoud van π rad.
 Aha, ik vond het al zo raar, ik gebruikte cos(2x + ¼π) = cos(½π) namelijk! Eerste had ik wel bedacht maar ik vond het zo raar dat die andere methode niet werkte. Maar die oplossingen kan je samenvoegen dus.Heel erg bedankt!quote:
Aha, ik vond het al zo raar, ik gebruikte cos(2x + ¼π) = cos(½π) namelijk! Eerste had ik wel bedacht maar ik vond het zo raar dat die andere methode niet werkte. Maar die oplossingen kan je samenvoegen dus.Heel erg bedankt!quote:Op woensdag 30 maart 2016 19:40 schreef Riparius het volgende:
[..]
Denk aan de eenheidscirkel: de cosinus van een rotatiehoek is per definitie de x-coördinaat van het beeldpunt van (1; 0) bij rotatie om de oorsprong over die hoek. Zie ook hier.
Welnu, als je het startpunt (1; 0) over ½π rad om de oorsprong roteert, dan kom je uit in het punt (0; 1) en de x-coördinaat van dat punt - en daarmee de cosinus van ½π - is dus inderdaad 0. Maar als je nu vervolgens nog over een geheel aantal halve slagen in tegenwijzerzin of in wijzerzin rond de oorsprong roteert, dan kom je óf weer uit op het punt (0;1) óf op het punt (0;−1) en ook dan is de x-coördinaat van het beeldpunt - en dus de cosinus - weer gelijk aan 0. Dus is
cos(2x + ¼π) = 0
equivalent met
2x + ¼π = ½π + kπ, k ∈ ℤ
[..]
Dat zou ook kunnen, maar is hier minder handig. Je kunt bedenken dat de cosinus van ½π gelijk is aan nul, zodat
cos(2x + ¼π) = 0
equivalent is met
cos(2x + ¼π) = cos(½π)
Nu zijn de cosinussen van twee (rotatie)hoeken gelijk als die (rotatie)hoeken hetzij aan elkaar gelijk zijn, hetzij elkaars tegengestelde zijn, afgezien van een geheel veelvoud van 2π, dus
cos α = cos β ⇔ α = β + k·2π ∨ α = −β + k·2π, k ∈ ℤ
zodat
cos(2x + ¼π) = cos(½π)
dus equivalent is met
2x + ¼π = ½π + 2kπ ∨ 2x + ¼π = −½π + 2kπ, k ∈ ℤ
en dit geeft
x = ⅛π + kπ ∨ x = −⅜π + kπ, k ∈ ℤ
Maar nu kun je bedenken dat het verschil tussen een rotatie over (1/8)·π rad en een rotatie over (−3/8)·π rad een rotatie is over ½π rad, en dat is de helft van π rad, zodat we de beide deeloplossingen hier samen kunnen voegen en de volledige oplossing dus eenvoudiger kunnen schrijven als
x = ⅛π + k·½π, k ∈ ℤ
Dit is uiteraard precies hetzelfde resultaat, maar je ziet nu dat het handiger is om gelijk te bedenken dat een cosinus van een rotatiehoek gelijk is aan nul als die rotatiehoek gelijk is aan ½π rad plus een geheel veelvoud van π rad.
 Ik heb een vraagstuk waar ik niet uitkom:
Ik heb een vraagstuk waar ik niet uitkom:
Een bal rolt over een veld met een beginsnelheid op tijdstip x=0s van 8m/s. Door wrijving krijgt de bal een vertraging van. Hoe ver rolt de bal?
Ik heb voor de snelheid de formuleopgesteld.
Hieruit haal ik V=
Deze zou ik dan toch gelijk moeten stellen aan 0? Omdat als de bal tot stilstand is gekomen de snelheid 0 is. Zodat ik de tijd (x) weet en deze in kan vullen in de formule voor de afgelegde weg.
[ Bericht 0% gewijzigd door Boarderzip op 02-04-2016 16:09:56 ]
 Geef indien mogelijk eens een scan van de originele opgave. Je uitdrukking voor de vertraging is wel heel merkwaadig. En in welke eenheid is die vertraging uitgedrukt?quote:
Geef indien mogelijk eens een scan van de originele opgave. Je uitdrukking voor de vertraging is wel heel merkwaadig. En in welke eenheid is die vertraging uitgedrukt?quote:Op zaterdag 2 april 2016 14:00 schreef Boarderzip het volgende:
Ik heb een vraagstuk waar ik niet uitkom:
Een bal rolt over een veld met een beginsnelheid op tijdstip x=0s van 8m/s. Door wrijving krijgt de bal een vertraging van. Hoe ver rolt de bal?
Als de beginsnelheid 8 m·s−1 bedraagt en de vertraging is bijvoorbeeld 2 m·s−2 dan is de bal na 8 m·s−1 : 2 m·s−2 = 4 seconden tot stilstand gekomen.
[ Bericht 0% gewijzigd door Riparius op 02-04-2016 15:36:13 ]
 Ik zie nu ook dat ik in de formule voor de vertraging de x vergeten was te noteren.quote:
Ik zie nu ook dat ik in de formule voor de vertraging de x vergeten was te noteren.quote:Op zaterdag 2 april 2016 15:29 schreef Riparius het volgende:
[..]
Geef indien mogelijk eens een scan van de originele opgave. Je uitdrukking voor de vertraging is wel heel merkwaadig. En in welke eenheid is die vertraging uitgedrukt?
Als de beginsnelheid 8 m·s−1 bedraagt en de vertraging is bijvoorbeeld 2 m·s−2 dan is de bal na 8 m·s−1 : 2 m·s−2 = 4 seconden tot stilstand gekomen.
Dit is de originele opgave, nummer 4:

 Nee, de opgave gebruikt de letter t voor de tijd en dan moet je daar niet een x van maken.quote:
Nee, de opgave gebruikt de letter t voor de tijd en dan moet je daar niet een x van maken.quote:Op zaterdag 2 april 2016 16:13 schreef Boarderzip het volgende:
Ik zie nu ook dat ik in de formule voor de vertraging de x vergeten was te noteren.
Geven we de snelheid (velocitas) op tijdstip t aan met v(t) en de versnelling (acceleratio) op tijdstip t met a(t) dan geldt
en dus
zodat
Nu is gegeven dat
en
zodat we dus hebben
Verder hebben we
en daarmee krijgen we
Nu moeten we bepalen voor welke waarde van t geldt v(t) = 0 en dan vinden we
De afstand die de bal heeft afgelegd vanaf het tijdstip t = 0 tot het moment dat de bal tot stilstand is gekomen op het tijdstip t = 5(10,42/3 − 4) vinden we nu door v(t) te integreren over het interval [0, 5(10,42/3 − 4)] en deze afstand bedraagt dus
oftewel ca. 15,51 meter (check).
[ Bericht 26% gewijzigd door Riparius op 03-04-2016 02:20:31 ]
 Heel hartelijk dankquote:
Heel hartelijk dankquote:Op zaterdag 2 april 2016 16:58 schreef Riparius het volgende:
[..]
Nee, de opgave gebruikt de letter t voor de tijd en dan moet je daar niet een x van maken.
Geven we de snelheid (velocitas) op tijdstip t aan met v(t) en de versnelling (acceleratio) op tijdstip t met a(t) dan geldt
en dus
zodat
Nu is gegeven dat
en
zodat we dus hebben
Verder hebben we
en daarmee krijgen we
Nu moeten we bepalen voor welke waarde van t geldt v(t) = 0 en dan vinden we
De afstand die de bal heeft afgelegd vanaf het tijdstip t = 0 tot het moment dat de bal tot stilstand is gekomen op het tijdstip t = 5(10,42/3 − 4) vinden we nu door v(t) te integreren over het interval [0, 5(10,42/3 − 4)] en deze afstand bedraagt dus
oftewel ca. 15,51 meter (check).het is me compleet duidelijk hoe je de som opbouwt, echter zie ik alleen nog niet hoe je de waarde van t berekent op v=0? Met behulp van een grafische rekenmachine krijg ik de juiste waarden voor t gevonden, maar op de hand krijg ik hem niet uitgewerkt.

 quote:
quote:Op zondag 3 april 2016 16:07 schreef Boarderzip het volgende:
[..]
Heel hartelijk dankhet is me compleet duidelijk hoe je de som opbouwt, echter zie ik alleen nog niet hoe je de waarde van t berekent op v=0? Met behulp van een grafische rekenmachine krijg ik de juiste waarden voor t gevonden, maar op de hand krijg ik hem niet uitgewerkt.
geeft
Beide leden vermenigvuldigen met 3/10 geeft
Nu beide leden verheffen tot de macht 2/3 en je hebt
De rest kun je nu zelf wel. Overigens is 10,42/3 lastig met de hand uit te rekenen (c.q. te benaderen). Met een (gewone) rekenmachine is dat uiteraard geen probleem.
 Super bedankt, ik ben er echt ontzettend mee geholpen!quote:
Super bedankt, ik ben er echt ontzettend mee geholpen!quote:Op zondag 3 april 2016 16:33 schreef Riparius het volgende:
[..]
geeft
Beide leden vermenigvuldigen met 3/10 geeft
Nu beide leden verheffen tot de macht 2/3 en je hebt
De rest kun je nu zelf wel. Overigens is 10,42/3 lastig met de hand uit te rekenen (c.q. te benaderen). Met een (gewone) rekenmachine is dat uiteraard geen probleem.
 Kan iemand mij hierbij helpen ?
Kan iemand mij hierbij helpen ?
log(x) + 1 = ln(x)
Ik kom niet verder dan deze stap, daarna lig ik er al uit
1 = ln(x) - log(x)
 Om dit op te lossen moet je de rekenregels voor logaritmen gebruiken.quote:
Om dit op te lossen moet je de rekenregels voor logaritmen gebruiken.quote:Op zondag 3 april 2016 22:35 schreef nickname89 het volgende:
Kan iemand mij hierbij helpen ?
log(x) + 1 = ln(x)
Ik kom niet verder dan deze stap, daarna lig ik er al uit
1 = ln(x) - log(x)
In dit geval heb je er twee nodig:
log a + log b = log ab
en
alog b = clog b / clog aOpinion is the medium between knowledge and ignorance (Plato)
 Dus dan verder:
Dus dan verder:
1= ln(x) - log(x)
1 = log(x) / log(e) - log(x)
log(10) = log(x) / log(e) - log(x)
10 = x/e - x
10 = x ( e-1)
10/(e-1) = x
x = 5,82
 Je uitwerking is fout. Je beweert hier dan wel dat je hebt leren rekenen met logaritmen, maar daar is niet veel van te merken.quote:
Je uitwerking is fout. Je beweert hier dan wel dat je hebt leren rekenen met logaritmen, maar daar is niet veel van te merken.quote:
Je kunt in je vergelijking niet zomaar alle log tekens in beide leden weglaten en dan verwachten dat je een equivalente vergelijking overhoudt. Ga maar na: Je hebt
log 2 + log 3 = log 6
en als je nu links en rechts alle log tekens weglaat krijg je volgens jouw logica
2 + 3 = 6
en dat klopt niet.
Los de vergelijking nu maar eens correct op.
 log(a) + log(b) = log(ab)
log(a) + log(b) = log(ab)
log(a) - log(b) = log(a/b)
Dus bij stap 3 naar 4 maak ik een fout
Dat wordt dan;
log(10) = ( log(x)/(log(e) ) / log(x))
log(10) = 1/(log(e)
Maar dat klopt niet
 Ik moet gokken wat je hier doet. maar ik denk dat je log(a)-log(b)=log(a/b) bij de stap (**) geïnterpreteerd hebt als log(a)-log(b)=log(a)/log(b), en dat gaat natuurlijk mis.quote:
Ik moet gokken wat je hier doet. maar ik denk dat je log(a)-log(b)=log(a/b) bij de stap (**) geïnterpreteerd hebt als log(a)-log(b)=log(a)/log(b), en dat gaat natuurlijk mis.quote:Op maandag 4 april 2016 11:51 schreef nickname89 het volgende:
log(a) + log(b) = log(ab)
log(a) - log(b) = log(a/b)
Dus bij stap 3 naar 4 maak ik een fout
Dat wordt dan;
(**)
log(10) = ( log(x)/(log(e) ) / log(x))
log(10) = 1/(log(e)
Maar dat klopt niet
Beginnen met
log(x) + 1 = ln(x)
levert achtereenvolgens
log(x)+log(10) = log(x)/log(e)
log(10x)=log(x1/log(e))
En dan kun je denk ik wel weer verder.Opinion is the medium between knowledge and ignorance (Plato)
 Nee, dat wordt het niet. Nu doe je net of (p/q) − p hetzelfde is als (p/q)/p.quote:
Nee, dat wordt het niet. Nu doe je net of (p/q) − p hetzelfde is als (p/q)/p.quote:Op maandag 4 april 2016 11:51 schreef nickname89 het volgende:
log(a) + log(b) = log(ab)
log(a) - log(b) = log(a/b)
Dus bij stap 3 naar 4 maak ik een fout
Dat wordt dan;
log(10) = ( log(x)/(log(e) ) / log(x))
Zorg nu eerst eens dat je een uitdrukking krijgt voor log(x). Dat is gewoon elementaire algebra.
 Ben opnieuw begonnen bij het begin, vind het moeilijk om verschillende logaritmes in een vergelijking te rangschikken, dus eerst meteen alles naar zelfde grondtal.
Ben opnieuw begonnen bij het begin, vind het moeilijk om verschillende logaritmes in een vergelijking te rangschikken, dus eerst meteen alles naar zelfde grondtal.
log(x) + 1 = ln(x)
ln(x) / ln(10) +1 = ln(x)
ln(x) = ( ln(x) - 1 ) ln(10)
ln(x) = 2,3ln(x) - 2,3
2,3 = 1,3ln(x)
1,77 = ln(x)
1,77 = elog(x)
e^1,77 = x
 Je mag geen benaderde waarden gebruiken. Isoleer nu eens netjes ln x, dan moet je uitkomen opquote:
Je mag geen benaderde waarden gebruiken. Isoleer nu eens netjes ln x, dan moet je uitkomen opquote:Op maandag 4 april 2016 12:43 schreef nickname89 het volgende:
Ben opnieuw begonnen bij het begin, vind het moeilijk om verschillende logaritmes in een vergelijking te rangschikken, dus eerst meteen alles naar zelfde grondtal.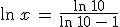

 Ik loop vast met mijn afstudeeronderzoek.
Ik loop vast met mijn afstudeeronderzoek.
Ik heb 2 groepen (Groep 1 en Groep 2). Een deel van de mensen van Groep 1 kan voorkomen in Groep 2.
Alleen moet ik nog wiskundig aantonen dat er Groep 2 niet kan bepalen door Groep 1 te vermenigvuldigen met een factor (omrekenfactor).
Ik weet echt niet welke richting qua statistiek ik het moet zoeken.It's called motorracing.Sorry? We went to carracing Toto
 Je moet juist aantonen dat groep 2 niet bepaald kan worden door te vermenigvuldigen met een factor.quote:
Je moet juist aantonen dat groep 2 niet bepaald kan worden door te vermenigvuldigen met een factor.quote:Op dinsdag 5 april 2016 16:02 schreef F1gamer het volgende:
Ik loop vast met mijn afstudeeronderzoek.
Ik heb 2 groepen (Groep 1 en Groep 2). Een deel van de mensen van Groep 1 kan voorkomen in Groep 2.
Alleen moet ik nog wiskundig aantonen dat er Groep 2 niet kan bepalen door Groep 1 te vermenigvuldigen met een factor (omrekenfactor).
Ik weet echt niet welke richting qua statistiek ik het moet zoeken.
Edit: laat maar, verkeerd gelezen.
 Hallo kan iemand mij helpen met de volgende differentiaalvergelijking, vraag e :
Hallo kan iemand mij helpen met de volgende differentiaalvergelijking, vraag e :
Ik zelf kwam tot dit, maar dit is jammer genoeg niet goed:
Het goede antwoord moet zijn: (1/ (1-Ct))
 Het is op zich goed wat je hebt, maar je moet nog wat extra stappen uitvoeren.quote:
Het is op zich goed wat je hebt, maar je moet nog wat extra stappen uitvoeren.quote:Op dinsdag 19 april 2016 11:03 schreef wiskunde3205 het volgende:
Hallo kan iemand mij helpen met de volgende differentiaalvergelijking, vraag e :
[ afbeelding ]
Ik zelf kwam tot dit, maar dit is jammer genoeg niet goed:
[ afbeelding ]
Het goede antwoord moet zijn: (1/ (1-Ct))
 Zou je me daar mee kunnen helpen? Ik heb al geprobeerd om log(x) om te zetten naar ln(x) maar daar kwam ik niet mee uit. Ik zat er ook aan te denken dat de i^2 misschien als constante kan worden opgevat..
Zou je me daar mee kunnen helpen? Ik heb al geprobeerd om log(x) om te zetten naar ln(x) maar daar kwam ik niet mee uit. Ik zat er ook aan te denken dat de i^2 misschien als constante kan worden opgevat..
 Je notatie is inconsequent. Je gebruikt in het linkerlid log en in het rechterlid ln maar in beide gevallen zijn het natuurlijke logaritmen. Verder vergeet je de absoluutstrepen in het linkerlid bij je uitwerking.quote:
Je notatie is inconsequent. Je gebruikt in het linkerlid log en in het rechterlid ln maar in beide gevallen zijn het natuurlijke logaritmen. Verder vergeet je de absoluutstrepen in het linkerlid bij je uitwerking.quote:Op dinsdag 19 april 2016 13:10 schreef wiskunde3205 het volgende:
[..]
Log(5) is toch niet gelijk aan ln(5) .. Dus wat bedoel je nu precies ?
 Oke, ik heb van de haakjes absoluutstreepjes gemaakt. Eerlijk gezegd heb ik nog steeds geen idee hoe ik nu verder moet
Oke, ik heb van de haakjes absoluutstreepjes gemaakt. Eerlijk gezegd heb ik nog steeds geen idee hoe ik nu verder moet
 Wel, je hebtquote:
Wel, je hebtquote:Op dinsdag 19 april 2016 13:30 schreef wiskunde3205 het volgende:
Oke, ik heb van de haakjes absoluutstreepjes gemaakt. Eerlijk gezegd heb ik nog steeds geen idee hoe ik nu verder moet
waarin K een constante is die positief, negatief, of nul kan zijn. Bedenk nu dat je kunt schrijven
waarin C = eK een positieve constante is. Kun je nu verder?
 Ja als ik dit moet oplossen :quote:
Ja als ik dit moet oplossen :quote:Op dinsdag 19 april 2016 13:37 schreef Riparius het volgende:
[..]
Wel, je hebt
waarin K een constante is die positief, negatief, of nul kan zijn. Bedenk nu dat je kunt schrijven
waarin C = eK een positieve constante is. Kun je nu verder?
Dan begrijp ik het wel. Ik snap alleen niet zo goed hoezo je de log mag veranderen in een ln?
 Je lijdt aan een misverstand. Het integreren van beide leden van je DV nadat je de variabelen hebt gescheiden levert zowel links als rechts een natuurlijke logaritme op. Hoe kom je erbij dat dat niet zo zou zijn?quote:
Je lijdt aan een misverstand. Het integreren van beide leden van je DV nadat je de variabelen hebt gescheiden levert zowel links als rechts een natuurlijke logaritme op. Hoe kom je erbij dat dat niet zo zou zijn?quote:Op dinsdag 19 april 2016 13:51 schreef wiskunde3205 het volgende:
[..]
Ja als ik dit moet oplossen :
Dan begrijp ik het wel. Ik snap alleen niet zo goed hoezo je de log mag veranderen in een ln?
 Ah, je hebt het linkerlid van je DV dus niet eens zelf (uitsluitend met pen en papier) uitgewerkt. Dat moet je natuurlijk wél doen.quote:
Ah, je hebt het linkerlid van je DV dus niet eens zelf (uitsluitend met pen en papier) uitgewerkt. Dat moet je natuurlijk wél doen.quote:Op dinsdag 19 april 2016 13:59 schreef wiskunde3205 het volgende:
Door deze website:
http://integrals.wolfram.(...)E2-x%29&random=false
In de zuivere wiskunde wordt meestal het symbool log gebruikt voor de natuurlijke logaritme, omdat logaritmen met andere grondtallen dan e voor de zuivere wiskunde niet echt van belang zijn. Het symbool ln voor de natuurlijke logaritme wordt vaak in de schoolwiskunde gebruikt, maar er zijn ook wel zuiver wiskundigen die het gebruiken voor de natuurlijke logaritme en dit is ook de officiële ISO recommendatie, zie hier.
 Voortaan gewoon alles met pen en papier uitwerken. Met breuksplitsing vind jequote:
Voortaan gewoon alles met pen en papier uitwerken. Met breuksplitsing vind jequote:Op dinsdag 19 april 2016 14:27 schreef wiskunde3205 het volgende:
Isgoed, iniedergeval bedankt voor je hulp !
en dan had je deze fout niet gemaakt.
 Van een logaritmisch spiraalvormige boog wil ik een functie voor hoek (beta) opstellen, welke op de boog staat. Zoals op de afbeelding is te zien, is het geen halve cirkel, maar loopt de straal vanuit het middelpunt steeds verder uit. Van deze boog heb ik de volgende functie:
Van een logaritmisch spiraalvormige boog wil ik een functie voor hoek (beta) opstellen, welke op de boog staat. Zoals op de afbeelding is te zien, is het geen halve cirkel, maar loopt de straal vanuit het middelpunt steeds verder uit. Van deze boog heb ik de volgende functie:
y = -0.0102x2 + 0.6883x + 55.105
r1 = 35 mm
r2 = 101 mm
beta 1 = 30 graden
beta 2 = 17 graden
alpha = 126,55 graden
De straal gaat dus van 35 mm naar 101 mm (vl nr).
De hoek beta gaat van 30 graden naar 17 graden (vl nr).
Nu heb ik een functie van de lijn, begin en eind waardes van de hoek en straal.
Mijn vraag is nu hoe ik met deze gegevens een functie voor beta kan opstellen die voor de gehele boog geldt?
een kromme plank is niet recht
 Je spiraal is geen logaritmische spiraal, want kenmerkend voor een logaritmische spiraal is nu juist dat de hoek die de straal naar een punt op de spiraal maakt met de raaklijn aan de spiraal in dat punt constant is. Verder is het volslagen onduidelijk hoe die betrekking tussen y en x in verband moet staan met je spiraal.quote:
Je spiraal is geen logaritmische spiraal, want kenmerkend voor een logaritmische spiraal is nu juist dat de hoek die de straal naar een punt op de spiraal maakt met de raaklijn aan de spiraal in dat punt constant is. Verder is het volslagen onduidelijk hoe die betrekking tussen y en x in verband moet staan met je spiraal.quote:Op zaterdag 23 april 2016 15:39 schreef PlankHout het volgende:
Van een logaritmisch spiraalvormige boog wil ik een functie voor hoek (beta) opstellen, welke op de boog staat. Zoals op de afbeelding is te zien, is het geen halve cirkel, maar loopt de straal vanuit het middelpunt steeds verder uit. Van deze boog heb ik de volgende functie:
y = -0.0102x2 + 0.6883x + 55.105

 Het is een spiraal, maar ik zou zo gauw niet weten of dit type spiraal een aparte naam heeft.quote:
Het is een spiraal, maar ik zou zo gauw niet weten of dit type spiraal een aparte naam heeft.quote:Op zaterdag 23 april 2016 16:47 schreef PlankHout het volgende:
Klopt inderdaad. Mijn hoek beta neemt af naarmate de straal toeneemt. Heet dit gewoon een boog?Je moet je eerst afvragen hoe je curve is gedefinieerd. Je zegt dat de hoek β afneemt naarmate r toeneemt, maar hoe is de relatie tussen β en r dan exact? Is dit een lineaire relatie? Of is het misschien zo dat de relatie tussen je hoek β en de rotatiehoek α nu juist lineair is? Allemaal vragen waar je eerst voor jezelf helderheid over moet krijgen. Zodra je exact weet hoe je curve is gedefinieerd kun je proberen een differentiaalvergelijking in poolcoördinaten voor je curve op te stellen. Als je die differentiaalvergelijking dan ook nog op kunt lossen heb je een vergelijking in poolcoördinaten voor je spiraal. Om inspiratie op te doen zou je deze oude post van mij eens door kunnen nemen, maar daar gaat het - inderdaad - om een logaritmische spiraal.quote:Ik heb in Excel een trendlijn van een boog gemaakt. Van de trendlijn kon ik de functie opvragen.
[ afbeelding ]
 Ik heb een vergelijking die ik op moet lossen. Ik wil de formule die ervoor zorgt dat ik X elke keer kan berekenen. De formule dus links, de X rechts. Ik weet dat X in het voorbeeld 0,4 moet zijn.
Ik heb een vergelijking die ik op moet lossen. Ik wil de formule die ervoor zorgt dat ik X elke keer kan berekenen. De formule dus links, de X rechts. Ik weet dat X in het voorbeeld 0,4 moet zijn.
De totale vergelijking is:
9800 = 2*(16*(0,02(1-0,02)/((0,02*X)^2)
Dus
9800/2/16=(0,02(1-0,02)/((0,02*X)^2)
9800/2/16=0,0196/(0,02X^2)
√(9800/2/16)=0,0196/0,02X
(√(9800/2/16))*50=0,0196/X
((√(9800/2/16))*50)X=0,0196
Maar dit komt niet uit. Ik maak ergens een grove denkfout, maar kan hem niet vinden. Hier ergens een equation genie?
[ Bericht 0% gewijzigd door Varr op 25-04-2016 22:19:05 ]
 x en * zijn multiplicatie?quote:
x en * zijn multiplicatie?quote:Op maandag 25 april 2016 22:03 schreef Varr het volgende:
Ik heb een vergelijking die ik op moet lossen. Ik wil de formule die ervoor zorgt dat ik X elke keer kan berekenen. De formule dus links, de X rechts. Ik weet dat X in het voorbeeld 0,4 moet zijn.
De totale vergelijking is:
9800 = 2x(16*(0,02(1-0,02)/((0,02*X)^2)
Dus
9800/2/16=(0,02(1-0,02)/((0,02*X)^2)
9800/2/16=0,0196/(0,02X^2)
√(9800/2/16)=0,0196/0,02X
(√(9800/2/16))*50=0,0196/X
((√(9800/2/16))*50)X=0,0196
Maar dit komt niet uit. Ik maak ergens een grove denkfout, maar kan hem niet vinden. Hier ergens een equation genie?
Dan krijg je 9800 = 1568/X^2
Al die haakjes zijn trouwens ook overbodig.
 Nee. Je notatie is inconsequent en je haakjes matchen niet. Je bedoelt kennelijkquote:
Nee. Je notatie is inconsequent en je haakjes matchen niet. Je bedoelt kennelijkquote:Op maandag 25 april 2016 22:03 schreef Varr het volgende:
Ik heb een vergelijking die ik op moet lossen. Ik wil de formule die ervoor zorgt dat ik X elke keer kan berekenen. De formule dus links, de X rechts. Ik weet dat X in het voorbeeld 0,4 moet zijn.
De totale vergelijking is:
9800 = 2x(16*(0,02(1-0,02)/((0,02*X)^2)
9800 = 2*(16*(0.02(1-0.02)/((0.02*x)^2)))
en dan vind je inderdaad x = 0.4 maar ook x = −0.4 (check). Dit is gewoon elementaire algebra.
 Excuus, ik heb het bericht aangepast, de eerste x moet inderdaad een * zijn.quote:
Excuus, ik heb het bericht aangepast, de eerste x moet inderdaad een * zijn.quote:Op maandag 25 april 2016 22:17 schreef t4rt4rus het volgende:
[..]
x en * zijn multiplicatie?
Dan krijg je 9800 = 1568/X^2
Al die haakjes zijn trouwens ook overbodig.
Zo is die inderdaad opgelost, ik heb echter de formule nodig [onbekend] = X.
De orginele formule is namelijk als volgt
D3 = D13*(16*POWER(SQRT(D1(1-D1)/D1*D2);2)
D1 = 0,02
D2 = 0,4
D3 = 9800
D13 = 2
Deze formule is dus om D3 op te lossen. Ik wil echter nu dezelfde formule, waarin D3 de bekende is, en D2 de onbekende.
 Je notatie is onduidelijk. Gebruik eens TeX om je formule leesbaar op te schrijven en gebruik indices voor je diverse parameters.quote:
Je notatie is onduidelijk. Gebruik eens TeX om je formule leesbaar op te schrijven en gebruik indices voor je diverse parameters.quote:Op maandag 25 april 2016 22:25 schreef Varr het volgende:
[..]
Excuus, ik heb het bericht aangepast, de eerste x moet inderdaad een * zijn.
Zo is die inderdaad opgelost, ik heb echter de formule nodig [onbekend] = X.
 Goed, je wil dus gewoon D2 uitdrukken in D1, D3 en D13. Kennelijk zit je een beetje te pielen met Excel, maar dan nog matchen je haakjes alweer niet, en bovendien is het onzinnig om eerst de vierkantswortel te trekken uit D1(1−D1) en het resultaat dan direct weer te kwadrateren.quote:
Goed, je wil dus gewoon D2 uitdrukken in D1, D3 en D13. Kennelijk zit je een beetje te pielen met Excel, maar dan nog matchen je haakjes alweer niet, en bovendien is het onzinnig om eerst de vierkantswortel te trekken uit D1(1−D1) en het resultaat dan direct weer te kwadrateren.quote:Op maandag 25 april 2016 22:25 schreef Varr het volgende:
[..]
Excuus, ik heb het bericht aangepast, de eerste x moet inderdaad een * zijn.
Zo is die inderdaad opgelost, ik heb echter de formule nodig [onbekend] = X.
De orginele formule is namelijk als volgt
D3 = D13*(16*POWER(SQRT(D1(1-D1)/D1*D2);2)
D1 = 0,02
D2 = 0,4
D3 = 9800
D13 = 2
Deze formule is dus om D3 op te lossen. Ik wil echter nu dezelfde formule, waarin D3 de bekende is, en D2 de onbekende.
Wat je kennelijk bedoelt is
Maar die haakjesorgie is hier overbodig aangezien we dit kunnen schrijven als
Nu delen we beide leden door D3 en vermenigvuldigen we tevens beide leden met D22 en dan hebben we
Aangenomen dat D2 positief is vinden we zo dus door de vierkantswortel te nemen van beide leden dat
Laten we nog even de proef op de som nemen door D13 = 2, D1 = 0,02 en D3 = 9800 in te vullen, dan vinden we
Voilà.
 9800 = 1568/X^2quote:
9800 = 1568/X^2quote:Op maandag 25 april 2016 22:25 schreef Varr het volgende:
[..]
Excuus, ik heb het bericht aangepast, de eerste x moet inderdaad een * zijn.
Zo is die inderdaad opgelost, ik heb echter de formule nodig [onbekend] = X.
X^2 = 1568/9800
X = +-√(1568/9800)
 Yesss het werkt, vielen dank! Even een breuk omzetten bleek toch wat lastiger dan gedacht na een paar jaar er niks mee gedaan te hebben.quote:
Yesss het werkt, vielen dank! Even een breuk omzetten bleek toch wat lastiger dan gedacht na een paar jaar er niks mee gedaan te hebben.quote:Op dinsdag 26 april 2016 03:52 schreef Riparius het volgende:
[..]
Goed, je wil dus gewoon D2 uitdrukken in D1, D3 en D13. Kennelijk zit je een beetje te pielen met Excel, maar dan nog matchen je haakjes alweer niet, en bovendien is het onzinnig om eerst de vierkantswortel te trekken uit D1(1−D1) en het resultaat dan direct weer te kwadrateren.
Wat je kennelijk bedoelt is
Maar die haakjesorgie is hier overbodig aangezien we dit kunnen schrijven als
Nu delen we beide leden door D3 en vermenigvuldigen we tevens beide leden met D22 en dan hebben we
Aangenomen dat D2 positief is vinden we zo dus door de vierkantswortel te nemen van beide leden dat
Laten we nog even de proef op de som nemen door D13 = 2, D1 = 0,02 en D3 = 9800 in te vullen, dan vinden we
Voilà.

 Dit moet je zo niet laten staan, want teller en noemer van je quotiënt bevatten een factor 2 en een factor 7² zodat 1568/9800 = 784/4900 = 16/100 en de vierkantswortel daaruit is 4/10. Dat ook 784 een factor 49 bevat was hier direct te zien omdat 784 = 800 − 16 = (50 − 1)·16.quote:
Dit moet je zo niet laten staan, want teller en noemer van je quotiënt bevatten een factor 2 en een factor 7² zodat 1568/9800 = 784/4900 = 16/100 en de vierkantswortel daaruit is 4/10. Dat ook 784 een factor 49 bevat was hier direct te zien omdat 784 = 800 − 16 = (50 − 1)·16.quote:Op dinsdag 26 april 2016 11:03 schreef t4rt4rus het volgende:
[..]
9800 = 1568/X^2
X^2 = 1568/9800
X = +-√(1568/9800)
 Er is een Wiskundepaniektopic in EXA.quote:
Er is een Wiskundepaniektopic in EXA.quote:Op vrijdag 29 april 2016 09:29 schreef t4rt4rus het volgende:
Het verbaast mij dat er nog geen eindexamen vragen komen.
 Een vraag van een oud tentamen vector calculus waar ik helaas de uitwerkingen niet van heb:
Een vraag van een oud tentamen vector calculus waar ik helaas de uitwerkingen niet van heb:
Gegeven de integraal
met D de bol
Vraag a:
Voor welke waarden van k (reeel getal) is de integraal eindig?
Nu heb ik als eerste de hele integraal omgeschreven naar sferische coördinaten, zodat volgt:
met als 'nieuw' domein:(Invoeren lukt me helaas niet zo mooi)
Nou lijkt het me duidelijk dat het gedeelte van phi eenvoudig geïntegreerd kan worden met de substitutiemethode, volgens mij kunnen er alleen problemen ontstaan bij het integreren van R waar de k instaat. Als integraal voor het R-gedeelte vind ik: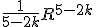
met bovengrens 1 en ondergrens 0.
Wat mij als eerste opvalt is dat 5-2k ongelijk moet zijn aan 0, anders vinden we slordig gezegd 'oneindig'. Ook moet 5-2k > 0, want anders zouden we bij het evalueren van de integraal delen door 0 en wederom 'oneindig' vinden.
Ik zou daarom zeggen dat de integraal eindig/convergent is voorkan iemand dit bevestigen of weerleggen?

 Ten eerste zit er een fout in de vraagstelling. De functie is niet gedefinieerd in (0,0,0), dus de integraal moet over D-{(0,0,0)} in plaats van D.
Ten eerste zit er een fout in de vraagstelling. De functie is niet gedefinieerd in (0,0,0), dus de integraal moet over D-{(0,0,0)} in plaats van D.
Verder moet je bij sferische coördinaten goed aangeven wat je grenzen zijn. In principe kan R niet van 0 naar 1 lopen, want een dergelijke coördinaatverandering werkt alleen over compacte gebieden. Je moet R dus van een r naar 1 laten lopen, met 0<r<1, en dan vervolgens een limiet r->0 nemen. Om convergentie na te gaan is het ook handiger om de integrand te vervangen door zijn absolute waarde (anders kunnen dingen nog steeds van de integratievolgorde afhangen en zo).
Goed, uiteindelijk gaat het erom voor welke waarde van α de integraalconvergeert. Dit is het geval als α>-1. Voor α=4-2k komt dat neer op k<5/2. Voor k=5/2 vind je overigens geen "oneindig", maar log(R), en de limiet naar 0 daarvan gaat naar -oneindig. Daarom convergeert het niet.

 Bedankt voor je reactie thabit!
Bedankt voor je reactie thabit!
Volgens mij kan ik uit jouw antwoord dus wel concluderen dat ik in essentie de vraag wel 'goed' heb aangepakt, op de ietwat slordige wiskundige notatie na maar daar ben ik natuurkundige voor . Even nog iets meer aandacht besteden aan de notatie van limieten enzovoorts dus.
Wel opmerkelijk om dan te zien dat voor k < 5/2 de integraal eindig is, voor k = 5/2 negatief oneindig en voor k > 5/2 positief oneindig.
 Hallo allemaal,
Hallo allemaal,
Ik heb een vraag over Taylor's inequality.
In deze opgave wordt gebruik gemaakt van het feit dat voor |x|<1 de remainder een bepaalde bovengrens heeft.
Volgens deze formule: http://mathworld.wolfram.com/TaylorsInequality.html wordt de maximale waarde van de n+1'ste afgeleide op e^1 gesteld, en er wordt dus gebruik gemaakt van |x|<1. Ik snap echter niet waar deze bovengrens vandaan komt.
Ik dacht dat je om de remainder te berekenen, de maximale waarde van de n+1'ste afgeleide op een bepaald interval moet evalueren. In deze vraag wordt echter geen interval gegeven, dus in principe zou de maximale waarde van e^x oneindig kunnen zijn in de plaats van e^1. Ik hoop dat een van jullie mij kan uitleggen waar de bovengrens van |x|<1 vandaan komt.
[ Bericht 1% gewijzigd door ulq op 22-05-2016 20:19:22 ]
 Als |x|<1, dan zit x dus op het interval [-1,1]. Maar het kan nog beter. In de opgave is x=-1, dus kun je het interval [-1,0] gebruiken. Op dit interval is ex hooguit 1. Je kunt hieruit dus direct de bovengrens 1/5! afleiden in plaats van e/5!.
Als |x|<1, dan zit x dus op het interval [-1,1]. Maar het kan nog beter. In de opgave is x=-1, dus kun je het interval [-1,0] gebruiken. Op dit interval is ex hooguit 1. Je kunt hieruit dus direct de bovengrens 1/5! afleiden in plaats van e/5!.
 Hmm oké, maar hoe leid je af dat x in het interval [-1,1] zit? Dat is niet gegeven in de opgave.quote:
Hmm oké, maar hoe leid je af dat x in het interval [-1,1] zit? Dat is niet gegeven in de opgave.quote:Op zondag 22 mei 2016 20:48 schreef thabit het volgende:
Als |x|<1, dan zit x dus op het interval [-1,1]. Maar het kan nog beter. In de opgave is x=-1, dus kun je het interval [-1,0] gebruiken. Op dit interval is ex hooguit 1. Je kunt hieruit dus direct de bovengrens 1/5! afleiden in plaats van e/5!.
 maw: Hoe kan je dit concluderen?quote:
maw: Hoe kan je dit concluderen?quote:Op zondag 22 mei 2016 20:48 schreef thabit het volgende:
In de opgave is x=-1, dus kun je het interval [-1,0] gebruiken.
 Ah wacht, ik denk dat ik het snap.
Ah wacht, ik denk dat ik het snap.
Je bekijkt natuurlijk de maximale fout van het taylorpolynoom in het punt x=-1. Dus ligt deze waarde maximaal 1 waarde van het punt a=0 af. En dat maakt het interval [-1,0]... (?)
Een andere vraag: is het dan niet sowieso ook zo dat de remainder die nu wordt berekend ook de werkelijke fout is in plaats van de maximale fout?
 Hmm, ik snap het niet helemaal.quote:
Hmm, ik snap het niet helemaal.quote:Op zondag 22 mei 2016 21:30 schreef thabit het volgende:
De restterm is es/5!, waar s ergens tussen a en x ligt (maar je weet niet waar precies).
Is het interval waarop je je Taylorpolynoom bekijkt (en dus de 'maximale waarde' voor de n+1'ste afgeleide van f(x) die hieruit volgt) per definitie gelijk aan het verschil tussen je x-waarde en je a-waarde?
 Het interval is het interval tussen a en x. Het verschil tussen x en a is een getal, en een interval is dat niet.
Het interval is het interval tussen a en x. Het verschil tussen x en a is een getal, en een interval is dat niet.
 Ah oké, dat bedoelde ikquote:
Ah oké, dat bedoelde ikquote:Op zondag 22 mei 2016 21:57 schreef thabit het volgende:
Het interval is het interval tussen a en x. Het verschil tussen x en a is een getal, en een interval is dat niet.
Maar waarom zouden ze dan e^1 als maximale waarde stellen? Het interval zou immers gelijk zijn aan [-1,0] en aangezien e^x strikt stijgend is, is e^0 de maximale waarde.
 Ze bekijken denk ik alles wat hooguit |x-a| van a afligt of zo. Dan krijg je [-1,1] in plaats van [-1,0].quote:
Ze bekijken denk ik alles wat hooguit |x-a| van a afligt of zo. Dan krijg je [-1,1] in plaats van [-1,0].quote:Op zondag 22 mei 2016 22:17 schreef ulq het volgende:
[..]
Ah oké, dat bedoelde ik
Maar waarom zouden ze dan e^1 als maximale waarde stellen? Het interval zou immers gelijk zijn aan [-1,0] en aangezien e^x strikt stijgend is, is e^0 de maximale waarde.
 Ik heb weer een nieuwe uitdaging. Dit is een zeer vergelijkbare formule:quote:
Ik heb weer een nieuwe uitdaging. Dit is een zeer vergelijkbare formule:quote:Op dinsdag 26 april 2016 03:52 schreef Riparius het volgende:
[..]
Goed, je wil dus gewoon D2 uitdrukken in D1, D3 en D13. Kennelijk zit je een beetje te pielen met Excel, maar dan nog matchen je haakjes alweer niet, en bovendien is het onzinnig om eerst de vierkantswortel te trekken uit D1(1−D1) en het resultaat dan direct weer te kwadrateren.
Wat je kennelijk bedoelt is
Maar die haakjesorgie is hier overbodig aangezien we dit kunnen schrijven als
Nu delen we beide leden door D3 en vermenigvuldigen we tevens beide leden met D22 en dan hebben we
Aangenomen dat D2 positief is vinden we zo dus door de vierkantswortel te nemen van beide leden dat
Laten we nog even de proef op de som nemen door D13 = 2, D1 = 0,02 en D3 = 9800 in te vullen, dan vinden we
Voilà.
Het Excel orgineel:
=D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
Op basis van jouw breuk vorige keer kan ik hier het volgende van malen (ik heb mijn best gedaan dit keer TeX te gebruiken):
Hierbij moet vermeld worden dat:
L3 uitschrijven in de orginele formule ging helaas niet, dan werd de breuk te lang en kapte hij hem af.
Nu is de vraag wederom:
Omdat er nu nog meer onbekenden rechts staan, heb ik echt geen flauw idee hoe ik heb moet oplossen.
 Deze formule is leesbaar, maar je hoeft geen externe server te gebruiken om TeX te gebruiken op FOK. Alles wat je hoeft te doen is de TeX tags gebruiken. Dus, bijvoorbeeld, als je dit in je bericht opneemt:quote:
Deze formule is leesbaar, maar je hoeft geen externe server te gebruiken om TeX te gebruiken op FOK. Alles wat je hoeft te doen is de TeX tags gebruiken. Dus, bijvoorbeeld, als je dit in je bericht opneemt:quote:Op woensdag 25 mei 2016 22:36 schreef Varr het volgende:
[..]
Ik heb weer een nieuwe uitdaging. Dit is een zeer vergelijkbare formule:
Het Excel orgineel:
=D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
Op basis van jouw breuk vorige keer kan ik hier het volgende van malen (ik heb mijn best gedaan dit keer TeX te gebruiken):
[ afbeelding ]
1 [tex]a = \frac{b}{c}[/tex]
dan krijg jeWat is hier staat is voor mij onleesbaar. Ik zie alleen een lange string van ogenschijnlijk willekeurige karakters.quote:Hierbij moet vermeld worden dat:
[snip]Dat is niet zo. Je kunt je betrekking herleiden tot een kwadratische vergelijking in L3. Weet je hoe je kwadratische vergelijkingen op kunt lossen?quote:L3 uitschrijven in de orginele formule ging helaas niet, dan werd de breuk te lang en kapte hij hem af.Dit is weer onleesbaar.quote:Nu is de vraag wederom:
[snip]Je wil kennelijk L3 uitdrukken in je overige variabelen. Hoeveel variabelen dat zijn maakt niet uit, want zoals gezegd kun je je betrekking herleiden tot een kwadratische vergelijking in L3 en daarvan kun je de oplossingen uitdrukken in de coëfficiënten van de vergelijking met behulp van de abc-formule. Dan moet je wel nagaan onder welke voorwaarden de discriminant van je vergelijking niet-negatief is en bekijken welk van de twee oplossingen je moet hebben als er bijvoorbeeld een positieve en een negatieve oplossing is en je alleen geïnteresseerd bent in de positieve oplossing.quote:Omdat er nu nog meer onbekenden rechts staan, heb ik echt geen flauw idee hoe ik het moet oplossen.
[ Bericht 0% gewijzigd door Riparius op 26-05-2016 04:20:28 ]
 Excuus, nu wel zichtbaar?quote:
Excuus, nu wel zichtbaar?quote:Op woensdag 25 mei 2016 23:31 schreef Riparius het volgende:
[..]
Deze formule is leesbaar, maar je hoeft geen externe server te gebruiken om TeX te gebruiken op FOK. Alles wat je hoeft te doen is de TeX tags gebruiken. Dus, bijvoorbeeld, als je dit in je bericht opneemt:
[ code verwijderd ]
dan krijg je
[..]
Wat is hier staat is voor mij onleesbaar. Ik zie alleen een lange string van ogenschijnlijk willekeurige karakters.
[..]
Dat is niet zo. Je kunt je betrekking herleiden tot een kwadratische vergelijking in L3. Weet je hoe je kwadratische vergelijkingen op kunt lossen?
[..]
Dit is weer onleesbaar.
[..]
Je wil kennelijk L3 uitdrukken in je overige variabelen. Hoeveel variabelen dat zijn maakt niet uit, want zoals gezegd kun je je betrekking herleiden tot een kwadratische vergelijking in L3 en daarvan kun je de oplossingen uitdrukken in de coëfficiënten van de vergelijking met behulp van de abc-formule. Dan moet je wel nagaan onder welke voorwaarden de discriminant van je vergelijking niet-negatief is en bekijken welk van de twee oplossingen je moet hebben als er bijvoorbeeld een positieve en een negatieve oplossing is en je alleen geïnteresseerd bent in de positieve oplossing.
Orginele Excel formule:
D3 =D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
Versimpeld in TeX:
Waar:
Het vraagstuk, als ik D2 als onbekende wil hebben i.p.v. D3, hoe wordt de formule dan?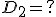

 Nu kom je weer net als vorige week pas met de juiste vraag nadat er al gereageerd is. Probeer de volgende keer je vraag te stellen in je eerste bericht...quote:
Nu kom je weer net als vorige week pas met de juiste vraag nadat er al gereageerd is. Probeer de volgende keer je vraag te stellen in je eerste bericht...quote:Op donderdag 26 mei 2016 09:33 schreef Varr het volgende:
[..]
Excuus, nu wel zichtbaar?
Orginele Excel formule:
D3 =D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
Versimpeld in TeX:
Waar:
Het vraagstuk, als ik D2 als onbekende wil hebben i.p.v. D3, hoe wordt de formule dan?
Laat dat excel nu eens even helemaal weg en stel gewoon de vraag.
Je tex komt totaal niet overeen met je excel formule. Dat kan je zelf toch ook zien?
En je twee links zijn nog steeds allemaal tekens.
Kom met:
Ik heb de vergelijking a = f(b, c, d, etc.)
En ik wil b als een functie van a, c, d, etc. schrijven.
En zorg er nu wel voor dat je formule klopt, dat Riparius je straks niet weer een uitgebreid antwoord geeft op een andere vraag dan je wil weten.
 De orginele formule laat ik liever niet weg, dan ben ik bang dat het omzetten naar TeX al fout gaat.quote:
De orginele formule laat ik liever niet weg, dan ben ik bang dat het omzetten naar TeX al fout gaat.quote:Op donderdag 26 mei 2016 10:56 schreef t4rt4rus het volgende:
[..]
Nu kom je weer net als vorige week pas met de juiste vraag nadat er al gereageerd is. Probeer de volgende keer je vraag te stellen in je eerste bericht...
Laat dat excel nu eens even helemaal weg en stel gewoon de vraag.
Je tex komt totaal niet overeen met je excel formule. Dat kan je zelf toch ook zien?
En je twee links zijn nog steeds allemaal tekens.
Kom met:
Ik heb de vergelijking a = f(b, c, d, etc.)
En ik wil b als een functie van a, c, d, etc. schrijven.
En zorg er nu wel voor dat je formule klopt, dat Riparius je straks niet weer een uitgebreid antwoord geeft op een andere vraag dan je wil weten.
Orginele Excel formule:
D3 =D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
Orgineel in TeX:
Hier is:
Ik wil weten:
De eerste stap in het versimpelen (o.b.v. de hulp Riparius van vorige keer, met een bijna dezelfde formule) is volgens mij:
 En wat kan je dan met D13 en die constanten doen?quote:
En wat kan je dan met D13 en die constanten doen?quote:Op donderdag 26 mei 2016 15:24 schreef Varr het volgende:
[..]
Orgineel in TeX:
Hier is:
Ik wil weten:
De eerste stap in het versimpelen (o.b.v. de hulp Riparius van vorige keer, met een bijna dezelfde formule) is volgens mij:
Klopt trouwens nog geen klote van die wortel en kwadraat.
 De vragensteller maakt niet duidelijk wat al die variabelen voorstellen en hoe hij tot zijn formule is gekomen en wat hij ermee wil bereiken. Dat zou hij eigenlijk wel moeten doen.quote:
De vragensteller maakt niet duidelijk wat al die variabelen voorstellen en hoe hij tot zijn formule is gekomen en wat hij ermee wil bereiken. Dat zou hij eigenlijk wel moeten doen.quote:Op donderdag 26 mei 2016 19:31 schreef t4rt4rus het volgende:
[..]
En wat kan je dan met D13 en die constanten doen?In het algemeen heb je voor elke reële xquote:Klopt trouwens nog geen klote van die wortel en kwadraat.
zodat het niet evident is dat de vierkantswortel uit dat kwadraat van zijn uitdrukking onder zijn wortelteken weer gelijk is aan die uitdrukking. Kennelijk zijn al zijn grootheden positief, maar daarmee is nog niet gezegd dat
ook steeds positief is.
 quote:
quote:Op dinsdag 26 april 2016 03:52 schreef Riparius het volgende:
[..]
Goed, je wil dus gewoon D2 uitdrukken in D1, D3 en D13. Kennelijk zit je een beetje te pielen met Excel, maar dan nog matchen je haakjes alweer niet, en bovendien is het onzinnig om eerst de vierkantswortel te trekken uit D1(1−D1) en het resultaat dan direct weer te kwadrateren.
Wat je kennelijk bedoelt is
Maar die haakjesorgie is hier overbodig aangezien we dit kunnen schrijven als
Nu delen we beide leden door D3 en vermenigvuldigen we tevens beide leden met D22 en dan hebben we
Aangenomen dat D2 positief is vinden we zo dus door de vierkantswortel te nemen van beide leden dat
Laten we nog even de proef op de som nemen door D13 = 2, D1 = 0,02 en D3 = 9800 in te vullen, dan vinden we
Voilà.De formule is niet van mezelf, het is een berekening om een sample size te berekenen voor een experiment.quote:Op donderdag 26 mei 2016 19:49 schreef Riparius het volgende:
[..]
De vragensteller maakt niet duidelijk wat al die variabelen voorstellen en hoe hij tot zijn formule is gekomen en wat hij ermee wil bereiken. Dat zou hij eigenlijk wel moeten doen.
[..]
In het algemeen heb je voor elke reële x
zodat het niet evident is dat de vierkantswortel uit dat kwadraat van zijn uitdrukking onder zijn wortelteken weer gelijk is aan die uitdrukking. Kennelijk zijn al zijn grootheden positief, maar daarmee is nog niet gezegd dat
ook steeds positief is.
De formule is bijna gelijk aan mijn vorige:
vorige
D3 = D13*(16*POWER(SQRT(D1(1-D1)/D1*D2);2)
huidige
D3 =D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
De vorige formule is toen als volgt opgelost:
Omdat de formule (for the untrained eye) zo weinig verschild, had ik verwacht dat ik deze op dezelfde manier (met jou stappen) kon oplossen. Echter omdat ik nu met D2 boven de breuk zit, weet ik niet hoe ik verder moet. Indien er nog informatie mist hoor ik het graag.
 Zit die D1*D2 in de noemer onder de wortel of niet?
Zit die D1*D2 in de noemer onder de wortel of niet?
En wat heb je zelf al geprobeerd?
Als je alleen het antwoord wil kan je het net zo goed in Mathematica gooien.
 Aangezien L3 afhangt van D2 moet je beginnen in je formule L3 te vervangen door D1(1 + D2) omdat je anders alleen een uitdrukking voor D2 af kunt leiden waarin L3 voorkomt, en dan kun je D2 nog steeds niet berekenen, omdat je immers L3 niet kent zonder D2 te kennen.quote:
Aangezien L3 afhangt van D2 moet je beginnen in je formule L3 te vervangen door D1(1 + D2) omdat je anders alleen een uitdrukking voor D2 af kunt leiden waarin L3 voorkomt, en dan kun je D2 nog steeds niet berekenen, omdat je immers L3 niet kent zonder D2 te kennen.quote:Op vrijdag 27 mei 2016 09:36 schreef Varr het volgende:
[..]
[..]
De formule is niet van mezelf, het is een berekening om een sample size te berekenen voor een experiment.
De formule is bijna gelijk aan mijn vorige:
vorige
D3 = D13*(16*POWER(SQRT(D1(1-D1)/D1*D2);2)
huidige
D3 =D13*((1,6449 + 0,84162)^2*POWER(SQRT(D1*(1-D1)+L3*(1-L3))/(D1*D2);2))
De vorige formule is toen als volgt opgelost:
Omdat de formule (for the untrained eye) zo weinig verschilt, had ik verwacht dat ik deze op dezelfde manier (met jou stappen) kon oplossen. Echter omdat ik nu met D2 boven de breuk zit, weet ik niet hoe ik verder moet. Indien er nog informatie mist hoor ik het graag.
Dit maakt dat deze opgave niet vergelijkbaar is met je vorige, maar een stuk lastiger. Je krijgt namelijk na herleiding een vierkantsvergelijking in D2 waarvan de coëfficiënten uitdrukkingen zijn in D1, D3, D13 en je constante C = (1,6449 + 0,84162)2.
Onder de aanname dat al je grootheden positief zijn en tevens onder de aanname dat (1 − D1) + L3(1 − L3) niet-negatief is zou je dan uit moeten komen op
Ga nu eerst maar eens netjes je uitdrukking herleiden om op deze vierkantsvergelijking in D2 uit te komen. Dat is louter elementaire algebra en daarmee niet moeilijk maar wel wat werk (wat ik dus ook heb gedaan). De volgende stap is dan het oplossen van deze vierkantsvergelijking, maar dat levert geen prettig hanteerbare uitdrukkingen op voor D2. Onder de aanname dat al je grootheden positief zijn kun je al zien dat er voor 0 < D1 < 1 één positieve oplossing zal zijn, aangezien het product van de beide oplossingen van deze vierkantsvergelijking dan negatief is omdat dit immers gelijk is aan (D12 − 1)/D12D22.
 Ik moet de afgeleide uit de volgende functie halen: H(u) = 1/2u + 1/(wortel van u) + 3. Ik ben hier al de hele middag mee bezig maar kom er gewoon niet uit. Heb dan ook al 6 jaar geen wiskunde gehad dus... Kan iemand me hiermee helpen?Shake with your right hand but hold a rock in the left.
Ik moet de afgeleide uit de volgende functie halen: H(u) = 1/2u + 1/(wortel van u) + 3. Ik ben hier al de hele middag mee bezig maar kom er gewoon niet uit. Heb dan ook al 6 jaar geen wiskunde gehad dus... Kan iemand me hiermee helpen?Shake with your right hand but hold a rock in the left.
 Het is handig om 1/(wortel van u) eerst als een macht van u te schrijven.quote:
Het is handig om 1/(wortel van u) eerst als een macht van u te schrijven.quote:Op vrijdag 10 juni 2016 18:13 schreef Teydelyk het volgende:
Ik moet de afgeleide uit de volgende functie halen: H(u) = 1/2u + 1/(wortel van u) + 3. Ik ben hier al de hele middag mee bezig maar kom er gewoon niet uit. Heb dan ook al 6 jaar geen wiskunde gehad dus... Kan iemand me hiermee helpen?
Daarna kun je de gewone regel voor differentieren toepassen.
 Bedankt!quote:
Bedankt!quote:Op vrijdag 10 juni 2016 18:17 schreef Lokasenna het volgende:
[..]
Het is handig om 1/(wortel van u) eerst als een macht van u te schrijven.
Daarna kun je de gewone regel voor differentieren toepassen.Shake with your right hand but hold a rock in the left.
 Ik heb even een kort vraagje, als ik de volgende formules op mijn gr(casio 9860) invoer bij graph.
Ik heb even een kort vraagje, als ik de volgende formules op mijn gr(casio 9860) invoer bij graph.
Y1=
Y2 =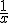
krijg ik dmv isct de punten x= -1.133 en x=1.133, terwijl ik met algebraïsche berekeningen uitkom op x=en x=
. Het antwoordenboek geeft dezelfde antwoorden als waar ik op uit kwam, weet er iemand wat ik verkeerd doe ik op mijn gr?

 Heel eenvoudig: je toetst kennelijk ln(x²) in daar waar je (ln(x))² bedoelt. Vergelijk dit met dit.quote:
Heel eenvoudig: je toetst kennelijk ln(x²) in daar waar je (ln(x))² bedoelt. Vergelijk dit met dit.quote:Op zaterdag 11 juni 2016 16:16 schreef kura-kura het volgende:
Ik heb even een kort vraagje, als ik de volgende formules op mijn gr(casio 9860) invoer bij graph.
Y1=
Y2 =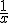
krijg ik dmv isct de punten x= -1.133 en x=1.133, terwijl ik met algebraïsche berekeningen uitkom op x=en x=
. Het antwoordenboek geeft dezelfde antwoorden als waar ik op uit kwam, weet er iemand wat ik verkeerd doe ik op mijn gr?

 2^-x = 2^(2 1/2)
2^-x = 2^(2 1/2)
-x = 2 1/2
Hoe werkt dit? Hoe wordt het bovenstaande het ondersteShake with your right hand but hold a rock in the left.
 Heel eenvoudig: zij a een positief reëel getal groter dan één en p en q twee andere (reële) grootheden. Als je nu hebtquote:
Heel eenvoudig: zij a een positief reëel getal groter dan één en p en q twee andere (reële) grootheden. Als je nu hebtquote:Op maandag 13 juni 2016 13:21 schreef Teydelyk het volgende:
2^-x = 2^(2 1/2)
-x = 2 1/2
Hoe werkt dit? Hoe wordt het bovenstaande het onderste
dan is
Je kunt gemakkelijk zien waarom dit zo is: p kan niet kleiner zijn dan q, want dan zou ap ook kleiner zijn dan aq en dat is niet zo, want er is gegeven dat ap = aq. Omgekeerd kan p ook niet groter zijn dan q, want dan zou ap ook groter zijn dan aq en dat is evenmin het geval. Dus blijft er maar één mogelijkheid over, namelijk dat p en q gelijk zijn.
Bovenstaande regel geldt overigens ook als a een positief reëel getal is kleiner dan 1, maar dan volgt uit p < q dat ap > aq en uit p > q dat ap < aq, zodat uit ap = aq wederom volgt dat p = q moet zijn.
Als je iets weet over functies: de functie f(x) = ax is strict monotoon stijgend op R voor a > 1 en strict monotoon dalend op R voor 0 < a < 1.
 Ik weet helemaal niets van wiskunde maar ik moet voor een hobbyproject (soort puzzeltocht) een formule samenstellen en nu heb ik geen idee of het klopt. Dit is wat ik heb...
Ik weet helemaal niets van wiskunde maar ik moet voor een hobbyproject (soort puzzeltocht) een formule samenstellen en nu heb ik geen idee of het klopt. Dit is wat ik heb...
(979 – 1986 : 6) : (7 + 5) - 6
-------------------------------------
16
De uitkomst zou 3 moeten zijn, kan een van jullie wiskunde bollebozen mij vertellen of dit klopt?
PS Ik ben nieuw op FOK!, please be gentle

 Je bedoelt kennelijkquote:
Je bedoelt kennelijkquote:
(((979 – (1986 : 6)) : (7 + 5)) - 6) : 16
Je vraag is zo niet goed te beantwoorden omdat je opgave zo ambigu is. Als je dit soort dingen intypt op een rekenmachine kan het zo maar zijn dat het ene merk rekenmachine een andere uitkomst geeft dan het andere merk rekenmachine.
Gebruik extra haakjes om de prioriteit van je bewerkingen eenduidig te maken als je je uitdrukking lineair opschrijft resp. invoert. Je kunt de uitkomst van je berekening dan controleren in WolframAlpha. Maar goed, je hebt inderdaad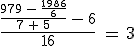

 Bedankt voor je heldere uitlegquote:
Bedankt voor je heldere uitlegquote:
Is er een duidelijkere manier om de formule weer te geven? Hoeft niet lineair, liefst niet zelfs...
 Ja, zoals ik het met TeX heb weergegeven hier op FOK. Als je het in WolframAlpha intypt krijg je dit.quote:
Ja, zoals ik het met TeX heb weergegeven hier op FOK. Als je het in WolframAlpha intypt krijg je dit.quote:Op vrijdag 17 juni 2016 15:56 schreef KW87 het volgende:
[..]
Bedankt voor je heldere uitleg
Is er een duidelijkere manier om de formule weer te geven? Hoeft niet lineair, liefst niet zelfs...
 Problem solved. Bedankt!quote:
Problem solved. Bedankt!quote:Op vrijdag 17 juni 2016 15:59 schreef Riparius het volgende:
[..]
Ja, zoals ik het met TeX heb weergegeven hier op FOK. Als je het in WolframAlpha intypt krijg je dit.
 Het eerste wat hier mis gaat is dat je niet eens de moeite neemt om uit te leggen wat de bedoeling is. Ik zie wel dat je s2 vervangt door 9 − x12 maar wat doe je dan? Je vervangt vervolgens elke term van je veelterm door het kwadraat van de betreffende term, maar waarom?quote:
Het eerste wat hier mis gaat is dat je niet eens de moeite neemt om uit te leggen wat de bedoeling is. Ik zie wel dat je s2 vervangt door 9 − x12 maar wat doe je dan? Je vervangt vervolgens elke term van je veelterm door het kwadraat van de betreffende term, maar waarom?quote:Op dinsdag 28 juni 2016 20:23 schreef wiskunde3205 het volgende:
Heey mensen weet iemand misschien waar het hier mis gaat:
[ afbeelding ]
 Ik wil de afgeleide er van gelijk stellen aan 0, dus probeer ik het eerst te vereenvoudigen. Waarom ik s2 gelijk stel aan 9-x1^2 is een vrij groot en lang verhaal waar het probleem niet zit. Het gaat ergens mis in de foto die ik heb geplaatst, vandaar mijn vraag over dat specifieke stuk.
Ik wil de afgeleide er van gelijk stellen aan 0, dus probeer ik het eerst te vereenvoudigen. Waarom ik s2 gelijk stel aan 9-x1^2 is een vrij groot en lang verhaal waar het probleem niet zit. Het gaat ergens mis in de foto die ik heb geplaatst, vandaar mijn vraag over dat specifieke stuk.
 Je vraag is zo niet te beantwoorden. Je differentieert je uitdrukking toch niet naar x1 door elke term te kwadrateren?quote:
Je vraag is zo niet te beantwoorden. Je differentieert je uitdrukking toch niet naar x1 door elke term te kwadrateren?quote:Op dinsdag 28 juni 2016 20:47 schreef wiskunde3205 het volgende:
Ik wil de afgeleide er van gelijk stellen aan 0, dus probeer ik het eerst te vereenvoudigen. Waarom ik s2 gelijk stel aan 9-x1^2 is een vrij groot en lang verhaal waar het probleem niet zit. Het gaat ergens mis in de foto die ik heb geplaatst, vandaar mijn vraag over dat specifieke stuk.
En nee, p + q − r is niet hetzelfde als p2 + q2 − r2 dus elke term domweg kwadrateren is geen geldige manier om je uitdrukking te vereenvoudigen.
 Ik ben nog niet begonnen met differentiëren, ik wilde het eerst vereenvoudigen maar het ging daar al mis.
Ik ben nog niet begonnen met differentiëren, ik wilde het eerst vereenvoudigen maar het ging daar al mis.
 Waar het mis gaat is denk ik bij 3* (9-x1^2)^(1/2), dat is volgens mij niet gelijk aan 9(9-x1^2), kan je me met dit gedeelte helpen?
Waar het mis gaat is denk ik bij 3* (9-x1^2)^(1/2), dat is volgens mij niet gelijk aan 9(9-x1^2), kan je me met dit gedeelte helpen?
 Nee, waar het misgaat is dat (a+b)^2 niet gelijk is aan a^2+b^2. Je kunt niet zomaar term voor term kwadrateren.quote:
Nee, waar het misgaat is dat (a+b)^2 niet gelijk is aan a^2+b^2. Je kunt niet zomaar term voor term kwadrateren.quote:Op dinsdag 28 juni 2016 21:01 schreef wiskunde3205 het volgende:
Waar het mis gaat is denk ik bij 3* (9-x1^2)^(1/2), dat is volgens mij niet gelijk aan 9(9-x1^2), kan je me met dit gedeelte helpen?
Werk de haakjes uit, vergeet dat hele kwadrateren/vereenvoudigen en ga gewoon stap voor stap differentiëren. Zo moeilijk is ie nu ook weer niet.Brutalen hebben de halve wereld; doe mij die andere helft dan maar
 Je kunt je uitdrukking in x1 het beste zo laten staan en dan termsgewijs differentiëren naar x1 en de verkregen afgeleide gelijk stellen aan 0. Dan heb je een vergelijking in x1 die je op kunt lossen.quote:
Je kunt je uitdrukking in x1 het beste zo laten staan en dan termsgewijs differentiëren naar x1 en de verkregen afgeleide gelijk stellen aan 0. Dan heb je een vergelijking in x1 die je op kunt lossen.quote:Op dinsdag 28 juni 2016 20:57 schreef wiskunde3205 het volgende:
Ik ben nog niet begonnen met differentiëren, ik wilde het eerst vereenvoudigen maar het ging daar al mis.
Bij een vergelijking met een wortelvorm kun je die wortel kwijtraken door de vergelijking eerst te herleiden tot een geschikte vorm en dan beide leden te kwadrateren. Waarschijnlijk was je daarmee in de war. Bedenk wel dat je de gevonden oplossingen van je vergelijking altijd moet controleren als je tijdens de oplossing van die vergelijking beide leden hebt gekwadrateerd: de gevonden oplossingen hoeven dan namelijk niet aan je oorspronkelijke vergelijking te voldoen.
 Wat je hier zegt snap ik ook en is ook niet wat ik doe. Wat ik doe is a * b = a^2 * b^2quote:
Wat je hier zegt snap ik ook en is ook niet wat ik doe. Wat ik doe is a * b = a^2 * b^2quote:Op dinsdag 28 juni 2016 21:03 schreef hooibaal het volgende:
[..]
Nee, waar het misgaat is dat (a+b)^2 niet gelijk is aan a^2+b^2. Je kunt niet zomaar term voor term kwadrateren.
Werk de haakjes uit, vergeet dat hele kwadrateren/vereenvoudigen en ga gewoon stap voor stap differentiëren. Zo moeilijk is ie nu ook weer niet.
 Het is niet wat je doet, en het is ook niet waar. 3 * 4 is zeker niet gelijk aan 3 * 3 * 4 * 4.quote:
Het is niet wat je doet, en het is ook niet waar. 3 * 4 is zeker niet gelijk aan 3 * 3 * 4 * 4.quote:Op dinsdag 28 juni 2016 21:08 schreef wiskunde3205 het volgende:
[..]
Wat je hier zegt snap ik ook en is ook niet wat ik doe. Wat ik doe is a * b = a^2 * b^2Brutalen hebben de halve wereld; doe mij die andere helft dan maar
 quote:
quote:Op dinsdag 28 juni 2016 21:09 schreef hooibaal het volgende:
[..]
Het is niet wat je doet, en het is ook niet waar. 3 * 4 is zeker niet gelijk aan 3 * 3 * 4 * 4.Nee I know ik noteerde het verkeerd het is: a * wortel(b) = a^2 * b maar dat is dus niet goed, maar vandaar mijn vraag dus ook op dit forum. Maar door te zeggen dat (a+b)^2 niet gelijk is aan a^2+b^2 wordt mijn probleem niet echt opgelostquote:Op dinsdag 28 juni 2016 21:09 schreef hooibaal het volgende:
[..]
Het is niet wat je doet, en het is ook niet waar. 3 * 4 is zeker niet gelijk aan 3 * 3 * 4 * 4.

 Je maakt een denkfout. Je kunt je uitdrukking die een functie is van x1 niet zomaar kwadrateren, want dan krijg je een andere functie en dat is niet de bedoeling. Kennelijk wil je die vierkantswortel wegwerken omdat je opziet tegen het differentiëren van je oorspronkelijke uitdrukking, maar zo werkt dat niet. Je moet eerst je uitdrukking differentiëren naar x1 en dan de verkregen afgeleide gelijk stellen aan nul en uit de aldus verkregen vergelijking x1 oplossen.quote:
Je maakt een denkfout. Je kunt je uitdrukking die een functie is van x1 niet zomaar kwadrateren, want dan krijg je een andere functie en dat is niet de bedoeling. Kennelijk wil je die vierkantswortel wegwerken omdat je opziet tegen het differentiëren van je oorspronkelijke uitdrukking, maar zo werkt dat niet. Je moet eerst je uitdrukking differentiëren naar x1 en dan de verkregen afgeleide gelijk stellen aan nul en uit de aldus verkregen vergelijking x1 oplossen.quote:Op dinsdag 28 juni 2016 21:14 schreef wiskunde3205 het volgende:
[..]
[..]
Nee I know ik noteerde het verkeerd het is: a * wortel(b) = a^2 * b maar dat is dus niet goed, maar vandaar mijn vraag dus ook op dit forum. Maar door te zeggen dat (a+b)^2 niet gelijk is aan a^2+b^2 wordt mijn probleem niet echt opgelost
 Kan iemand de integraal van e^(1-t) dt stap voor stap uitleggen? Ik kom met substitutie uit op e^(1-t), terwijl het antwoord -e^(1-t) is.
Kan iemand de integraal van e^(1-t) dt stap voor stap uitleggen? Ik kom met substitutie uit op e^(1-t), terwijl het antwoord -e^(1-t) is.
 Laat eens zien wat je gedaan hebt, anders kan niemand met zekerheid zeggen wat je fout doet.quote:
Laat eens zien wat je gedaan hebt, anders kan niemand met zekerheid zeggen wat je fout doet.quote:Op zaterdag 9 juli 2016 23:07 schreef DrNick het volgende:
Kan iemand de integraal van e^(1-t) dt stap voor stap uitleggen? Ik kom met substitutie uit op e^(1-t), terwijl het antwoord -e^(1-t) is.
Als je u = 1 − t substitueert, dan is du/dt = −1 en dus dt = −du zodat je krijgt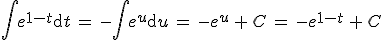

 Ah, ik had du/dt verkeerd gedifferentieerd. Thanksquote:
Ah, ik had du/dt verkeerd gedifferentieerd. Thanksquote:Op zondag 10 juli 2016 01:14 schreef Riparius het volgende:
[..]
Laat eens zien wat je gedaan hebt, anders kan niemand met zekerheid zeggen wat je fout doet.
Als je u = 1 − t substitueert, dan is du/dt = −1 en dus dt = −du zodat je krijgt

 Hallo allen!
Hallo allen!
Ik zit het met het volgende.... Het betreft over expected utility..
Weet iemand hoe je op 0,39 en 0.00007 komt, evenals hoe je op de alinea van ''Then...'' komt?
De literatuurpagina waar in details meer op in wordt gegaan op de vraag op de slide:
Ik snap dus totaal niet hoe ze op de volgende getallen komen van dit stukje uit de tekst:
if you have the same aversion to the lose $10/gain $11 bet at wealth level W+ 21, then you value dollar W+ 21 + 11 = W+ 32 by at most 10/11 as you value dollar W+ 21 -10 = W+ 11,which means you value dollar W+ 32 by at most 10/11 * 10/11 = 5/6 as much as dollar W-10. You will value the W + 210th dollar by at most 40 percent as much as dollar
W-10, and the W + 900th dollar by at most 2 percent as much as dollar W-10. In words, rejecting the 50-50 lose $10/gain $11 gamble implies a 10 percent decline in marginal utility for each $21 in additional lifetime wealth
 100 / 1,09 = 91,74
100 / 1,09 = 91,74
100 * 0,90 = 90,00
Mensen gebruiken verschillende manieren om 90% van 100 uit te rekenen, maar mijn inziens is 90% van 100 --> 90
Waarom wijkt die bovenste dan af
Ik ben confusedIk moest de groeten doen van Kapitein Ortega.
 Die bovenste is echt gewoon iets compleet anders dan ergens 90% van nemen lieve Pris.quote:
Die bovenste is echt gewoon iets compleet anders dan ergens 90% van nemen lieve Pris.quote:Op dinsdag 6 september 2016 08:34 schreef PrisTheShiz het volgende:
100 / 1,09 = 91,74
100 * 0,90 = 90,00
Mensen gebruiken verschillende manieren om 90% van 100 uit te rekenen, maar mijn inziens is 90% van 100 --> 90
Waarom wijkt die bovenste dan af
Ik ben confused

 Pris Ham, samen tosti.maken?quote:
Pris Ham, samen tosti.maken?quote:Op dinsdag 6 september 2016 09:03 schreef Kaas- het volgende:
[..]
Die bovenste is echt gewoon iets compleet anders dan ergens 90% van nemen lieve Pris. Ik moest de groeten doen van Kapitein Ortega.
Ik moest de groeten doen van Kapitein Ortega.
 Als je op de lagere school goed had leren rekenen had je niet van dit soort onzin uitgekraamd.quote:
Als je op de lagere school goed had leren rekenen had je niet van dit soort onzin uitgekraamd.quote:Op dinsdag 6 september 2016 08:34 schreef PrisTheShiz het volgende:
100 / 1,09 = 91,74
100 * 0,90 = 90,00
Mensen gebruiken verschillende manieren om 90% van 100 uit te rekenen, maar mijn inziens is 90% van 100 --> 90
Waarom wijkt die bovenste dan af
Ik ben confused
Delen is hetzelfde als vermenigvuldigen met het omgekeerde, maar het omgekeerde van 0,9 is niet 1,09 en dus is 100 / 1,09 ook niet hetzelfde als 100 * 0,9.
 quote:
quote:Op dinsdag 6 september 2016 18:27 schreef Riparius het volgende:
[..]
Als je op de lagere school goed had leren rekenen had je niet van dit soort onzin uitgekraamd.
Delen is hetzelfde als vermenigvuldigen met het omgekeerde, maar het omgekeerde van 0,9 is niet 1,09 en dus is 100 / 1,09 ook niet hetzelfde als 100 * 0,9.die opmerking is echt nergens voor nodig.
Maar bedankt voor je uitleg
Ik was even confused. Maar het is opgelost
[ Bericht 7% gewijzigd door KapiteinIglo op 06-09-2016 19:17:54 ]Ik moest de groeten doen van Kapitein Ortega.
 Ik heb een wiskundevraagje voor jullie.
Ik heb een wiskundevraagje voor jullie.
Ik heb 30 noten en 3 apen, een aap kan maximaal 20 nootjes krijgen. Op hoeveel manieren kan ik de nootjes verdelen over de drie apen?
Aap 1: 20
Aap 2: 5
Aap 3: 5
is een andere verdeling dan
Aap 1: 5
Aap 2: 20
Aap 3: 5
edit; het gaat over hele getallen - er worden geen halve nootjes uitgedeeld
edit 2; iedere aap krijgt minimaal 1 nootje
[ Bericht 8% gewijzigd door VanKuikeren op 08-09-2016 15:20:19 ]
 De vraagstelling is nog niet precies genoeg: je moet je ook nog aangeven of het wel of niet is toegestaan dat een aap helemaal geen nootje krijgt.quote:
De vraagstelling is nog niet precies genoeg: je moet je ook nog aangeven of het wel of niet is toegestaan dat een aap helemaal geen nootje krijgt.quote:Op donderdag 8 september 2016 14:59 schreef VanKuikeren het volgende:
Ik heb een wiskundevraagje voor jullie.
Ik heb 30 noten en 3 apen, een aap kan maximaal 20 nootjes krijgen. Op hoeveel manieren kan ik de nootjes verdelen over de drie apen?
edit; het gaat over hele getallen - er worden geen halve nootjes uitgedeeld
[ Bericht 1% gewijzigd door Riparius op 08-09-2016 15:49:26 ]
 zie mijn editsquote:
zie mijn editsquote:Op donderdag 8 september 2016 15:24 schreef Riparius het volgende:
[..]
De vraagstelling is nog niet precies genoeg: je moet je ook nog aangeven of het wel of niet is toegestaan dat één of twee apen helemaal geen nootje krijgen.

 Laat eerst eens zien wat je zelf hebt gedaan om het vraagstuk op te lossen. Bedenk dat het aantal nootjes dat de derde aap krijgt vastligt zodra je hebt bepaald hoeveel nootjes de eerste aap krijgt en hoeveel nootjes de tweede aap krijgt.quote:
Laat eerst eens zien wat je zelf hebt gedaan om het vraagstuk op te lossen. Bedenk dat het aantal nootjes dat de derde aap krijgt vastligt zodra je hebt bepaald hoeveel nootjes de eerste aap krijgt en hoeveel nootjes de tweede aap krijgt.quote:
 Ik had dit gemaakt om te kijken of ik een patroon kon ontdekken https://gyazo.com/4461b5d4d13547bcee42ba1a225f0c78quote:
Ik had dit gemaakt om te kijken of ik een patroon kon ontdekken https://gyazo.com/4461b5d4d13547bcee42ba1a225f0c78quote:Op donderdag 8 september 2016 15:40 schreef Riparius het volgende:
[..]
Laat eerst eens zien wat je zelf hebt gedaan om het vraagstuk op te lossen. Bedenk dat het aantal nootjes dat de derde aap krijgt vastligt zodra je hebt bepaald hoeveel nootjes de eerste aap krijgt en hoeveel nootjes de tweede aap krijgt.
Als ik kijk naar hoe jij het formuleert:
Zijn er max 29 nootjes te verdelen over de twee apen - waarvan max 20 voor een aap.
20 = 9 opties *3?
19 = 10 opties *3?
18 = 11 opties *3?
etc? en dan optellen? geen idee
edit; hier klopt geen kont van waarschijnlijk
edit2; 20*29?
[ Bericht 1% gewijzigd door VanKuikeren op 08-09-2016 16:22:48 ]
 Bekijk eerst eens hoeveel mogelijkheden je hebt als de eerste aap 1 t/m 9 nootjes krijgt (9 situaties). Bekijk vervolgens hoeveel mogelijkheden je hebt als de eerste aap 10 t/m 20 nootjes krijgt (11 situaties). Tel deze aantallen mogelijkheden dan op.
Bekijk eerst eens hoeveel mogelijkheden je hebt als de eerste aap 1 t/m 9 nootjes krijgt (9 situaties). Bekijk vervolgens hoeveel mogelijkheden je hebt als de eerste aap 10 t/m 20 nootjes krijgt (11 situaties). Tel deze aantallen mogelijkheden dan op.
 1 tm 9:quote:
1 tm 9:quote:Op donderdag 8 september 2016 16:24 schreef Riparius het volgende:
Bekijk eerst eens hoeveel mogelijkheden je hebt als de eerste aap 1 t/m 9 nootjes krijgt (9 situaties). Bekijk vervolgens hoeveel mogelijkheden je hebt als de eerste aap 10 t/m 20 nootjes krijgt (11 situaties). Tel deze aantallen mogelijkheden dan op.
1 - (20,9) (19,10) (18,11) (17,12) (16,13) (15,14) (14,15) (13,16) (12,17) (11,18) (10,19) (9, 20) = 12
2 - (20,8) (19,9) (18,10) (17,11) (16,12) (15,13) (14,14) (13,15) (12,16) (11,17) (10, 18) (9,19) (8,20) = 13
3 - (20,7) (19,8) (18,9) (17,10) (16,11) (15,12) (14,13) (13,14) (12,15) (11,16) (10,17) (9,18) (8,19)(7,20) = 14
4 = 15
5 = 16
6 = 17
7 = 18
8 = 19
9 = 20
------------------------ = 144
10 = (1, 19) (2,18) (3,17) (4,16) (5,15) (6,14) (7,13) (8,12) (9,11) (10,10) + 9 = 19 opties
11 = (1, 18) (2, 17) (3,16) (4,15) (5,14) (6,13) (7,12) (8,11) (9,10) *2 = 18 opties
12 = 17
13 = 16
14 = 15
15 = 14
16 = 13
17 = 12
18 = 11
19 = 10
20 = 9
----------------------- = 154
= 298
Is dat het antwoord? en hoe krijg ik dat uit (in) een formule?
[ Bericht 33% gewijzigd door VanKuikeren op 08-09-2016 16:45:31 ]
 Je hoeft alleen te kijken naar de aantallen nootjes die de eerste en de tweede aap krijgen, want het aantal nootjes dat de derde aap krijgt ligt dan vast.
Je hoeft alleen te kijken naar de aantallen nootjes die de eerste en de tweede aap krijgen, want het aantal nootjes dat de derde aap krijgt ligt dan vast.
 Weet je wat een rekenkundige reeks is? En hoe je die sommeert?quote:
Weet je wat een rekenkundige reeks is? En hoe je die sommeert?quote:Op donderdag 8 september 2016 16:40 schreef VanKuikeren het volgende:
Is dat het antwoord? en hoe krijg ik dat uit (in) een formule?
 I see.quote:
I see.quote:Op donderdag 8 september 2016 16:53 schreef Riparius het volgende:
Je hoeft alleen te kijken naar de aantallen nootjes die de eerste en de tweede aap krijgen, want het aantal nootjes dat de derde aap krijgt ligt dan vast.Niet meer dan ik net op wikipedia heb gelezen en nee.quote:Op donderdag 8 september 2016 17:16 schreef Riparius het volgende:
[..]
Weet je wat een rekenkundige reeks is? En hoe je die sommeert?
 Om een rekenkundige reeks te sommeren neem je de som van de eerste en de laatste term, vermenigvuldig je de uitkomst met het aantal termen en deel je het resultaat van die vermenigvuldiging door 2. Anders gezegd, je hebtquote:
Om een rekenkundige reeks te sommeren neem je de som van de eerste en de laatste term, vermenigvuldig je de uitkomst met het aantal termen en deel je het resultaat van die vermenigvuldiging door 2. Anders gezegd, je hebtquote:Op donderdag 8 september 2016 17:24 schreef VanKuikeren het volgende:
[..]
I see.
[..]
Niet meer dan ik net op wikipedia heb gelezen en nee.
t1 + t2 + ... + tn-1 + tn = ½n(t1 + tn)
Zie je ook waarom dit zo werkt?
 Som eerste en laatste term (20+1) *20 = 420quote:
Som eerste en laatste term (20+1) *20 = 420quote:Op donderdag 8 september 2016 17:31 schreef Riparius het volgende:
[..]
Om een rekenkundige reeks te sommeren neem je de som van de eerste en de laatste term, vermenigvuldig je de uitkomst met het aantal termen en deel je het resultaat van die vermenigvuldiging door 2. Anders gezegd, je hebt
t1 + t2 + ... + tn-1 + tn = ½n(t1 + tn)
Zie je ook waarom dit zo werkt?
420/ 2 = 210
=/= 298?
 Nee, je hebt te maken met twee rekenkundige rijen (zie je eigen berekening). Die moet je elk apart sommeren.quote:
Nee, je hebt te maken met twee rekenkundige rijen (zie je eigen berekening). Die moet je elk apart sommeren.quote:Op vrijdag 9 september 2016 12:01 schreef VanKuikeren het volgende:
[..]
Som eerste en laatste term (20+1) *20 = 420
420/ 2 = 210
=/= 298?
 Hoe los ik dit op?
Hoe los ik dit op?
F1*cos(a)=539,62
F1*sin(a)=493,01
Pogingen tot omschrijven wordt het bij mij alleen maar ingewikkelder van..
 Als ik er op de gok vanuit ga dat F1 gewoon een getalletje is, dan kun je de eerste vergelijking omschrijven inquote:
Als ik er op de gok vanuit ga dat F1 gewoon een getalletje is, dan kun je de eerste vergelijking omschrijven inquote:Op woensdag 14 september 2016 15:50 schreef jevl het volgende:
Hoe los ik dit op?
F1*cos(a)=539,62
F1*sin(a)=493,01
Pogingen tot omschrijven wordt het bij mij alleen maar ingewikkelder van..
F1 = 539,62/cos(a) (merk op dat dit mag, omdat de vergelijking toch geen oplossing heeft in situaties waarbij cos(a)=0)
Die substitueren in de tweede levert
539,62*sin(a)/cos(a)=493,01, oftewel
539,62*tan(a) =493,01.
Nu moet je denk ik wel verder kunnen.Opinion is the medium between knowledge and ignorance (Plato)
 Heeft iemand een idee wat de betekenis van dit gedicht zou kunnen zijn?? Ik moet er een presentatie over houden over een paar dagen, het gedicht heet "Giro giro tondo" van Ilja Leonard Pfeijffer.
Heeft iemand een idee wat de betekenis van dit gedicht zou kunnen zijn?? Ik moet er een presentatie over houden over een paar dagen, het gedicht heet "Giro giro tondo" van Ilja Leonard Pfeijffer.
Al had ik volgens mij niets raars gezegd,
was jij geërgerd. Jij wilde ontbijten.
Je strooide crackers onder met verwijten,
totdat er echt iets misging, maar dan echt.
Er ging nog net geen strijkbout door het raam.
De vaas van oma wankelde vervaarlijk.
Het stille mes werd bijna nog gevaarlijk.
Maar jij verbeet mijn staren, ik je naam.
Ik had je net iets meer als mij verzonnen,
als wie mijn surreële dromen deelt
en midscheeps rum rolt in beslagen tonnen.
Wat liefde heet te heten, is wat scheelt
aan wat er is nadat het is begonnen.
We scheppen wie ons liefheeft naar ons beeld.
 Ooooooooooooooooooooooooo aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaahhhhhhh
Ooooooooooooooooooooooooo aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaahhhhhhh
 In de wiskundeles?quote:
In de wiskundeles?quote:Op zondag 2 oktober 2016 21:13 schreef L.V.D. het volgende:
Ik moet er een presentatie over houden over een paar dagen,Opinion is the medium between knowledge and ignorance (Plato)
 Ik zag na ik het had gepost pas dat dit voor wiskunde alleen is haha, mijn excusesquote:Ooooooooooooooooooooooooo aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaahhhhhhh
Ik zag na ik het had gepost pas dat dit voor wiskunde alleen is haha, mijn excusesquote:Ooooooooooooooooooooooooo aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaahhhhhhh
 Hoi hoi,
Hoi hoi,
Ik heb momenteel het vak differentiaal vergelijkingen en de professor schrijft regelmatig vergelijking zoals: om naar
Om het zelf te snappen heb ik dit ook even geprobeerd, maar ik eindig op Deze laatste twee termen kan ik niet meer omschrijven naar Sinh, want volgens de regels moet er een minus in een van de twee exponenten staan. Wat doe ik hier fout?SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.leef de leven
 quote:
quote:Op zondag 9 oktober 2016 14:30 schreef RRuben het volgende:
Hoi hoi,
Ik heb momenteel het vak differentiaal vergelijkingen en de professor schrijft regelmatig vergelijking zoals: [ afbeelding ] om naar [ afbeelding ]
Om het zelf te snappen heb ik dit ook even geprobeerd, maar ik eindig op [ afbeelding ] Deze laatste twee termen kan ik niet meer omschrijven naar Sinh, want volgens de regels moet er een minus in een van de twee exponenten staan. Wat doe ik hier fout?Als je de juiste coëfficiënten vindt moet dat toch wel lukken?SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
a cosh x + b sinh x = (a+b)/2 e^x + (a-b)/2 e^{-x}
 Ah zo werkt ie dus wel, thanks!quote:
Ah zo werkt ie dus wel, thanks!quote:Op zondag 9 oktober 2016 21:56 schreef t4rt4rus het volgende:
[..]
Als je de juiste coëfficiënten vindt moet dat toch wel lukken?
a cosh x + b sinh x = (a+b)/2 e^x + (a-b)/2 e^{-x}leef de leven
 Dus dan krijg jequote:
Dus dan krijg jequote:
(C2 + C3 - C5) cosh 3x + (C2 - C5) sinh 3x
-edit-
Alles is nog veel makkelijker
e^x = cosh x + sinh x
e^-x = cosh x - sinh x
Dus
a e^x + b e^-x = (a+b) cosh x + (a-b) sinh x
[ Bericht 9% gewijzigd door t4rt4rus op 09-10-2016 23:39:57 ]
 Bij het programmeren op de GRM kan je bij de TI-84 een commando [PAUSE] gebruiken. Het programma stopt dan, tot de gebruiker met een druk op [Enter] aangeeft dat het verder mag gaan.
Bij het programmeren op de GRM kan je bij de TI-84 een commando [PAUSE] gebruiken. Het programma stopt dan, tot de gebruiker met een druk op [Enter] aangeeft dat het verder mag gaan.
Weet iemand waar ze datzelfde commando op de CASIO hebben verstopt?
En ten tweede: er is een Zebraboekje "Simuleren met Kansen", (of iets dergelijks) waarbij ze een programmaatje maken (op de Texas) waarbij toevalsgetallen( 1 tot 6, het is een dobbelsteen) in lijsten worden geteld, en tot slot worden de resultaten na een x aantal worpen (gebruiker mag variabele ingeven) absoluut en percentueel getoond. (Wel zelf commando [ClrAll Lists] aan het begin toevoegen, anders ga je een tweede simulatie met vervuilde lijsten in). Klopt het dat een soortgelijk programmaatje op de CASIO niet te programmeren is?
 ah ok, super bedankt!quote:
ah ok, super bedankt!quote:Op zondag 9 oktober 2016 22:45 schreef t4rt4rus het volgende:
[..]
Dus dan krijg je
(C2 + C3 - C5) cosh 3x + (C2 - C5) sinh 3x
-edit-
Alles is nog veel makkelijker
e^x = cosh x + sinh x
e^-x = cosh x - sinh x
Dus
a e^x + b e^-x = (a+b) cosh x + (a-b) sinh xleef de leven
 Kan iemand mij vertellen of bussommen op het wiskunde eindexamen van vmbo gl/tl fout worden gerekend? Ik kan mij herinneren dat ik dit een keer ergens gelezen heb maar kan dit niet terug vinden.
Kan iemand mij vertellen of bussommen op het wiskunde eindexamen van vmbo gl/tl fout worden gerekend? Ik kan mij herinneren dat ik dit een keer ergens gelezen heb maar kan dit niet terug vinden.
*edit: Ik heb wel een document gevonden uit 2014, waar ik het in gelezen heb. Maar mijn vraag blijft staan: is dit nou wel / niet toegestaan op de huidige eindexamens
Dit bedoel ik met bussom: als je bij het berekenen van een driehoek opschrijft:
Opp driehoek ABC = 5 * 2 = 10 / 2 = 5 vierkante centimeter.
[ Bericht 25% gewijzigd door Silverdigger2 op 11-10-2016 15:45:01 ]
 Dat noemen we ook wel breien. Maar als je al weet dat het niet mag, doe het dan gewoon niet. In feite schrijf je namelijk onwaarheden op.quote:
Dat noemen we ook wel breien. Maar als je al weet dat het niet mag, doe het dan gewoon niet. In feite schrijf je namelijk onwaarheden op.quote:Op dinsdag 11 oktober 2016 15:31 schreef Silverdigger2 het volgende:
Kan iemand mij vertellen of bussommen op het wiskunde eindexamen van vmbo gl/tl fout worden gerekend? Ik kan mij herinneren dat ik dit een keer ergens gelezen heb maar kan dit niet terug vinden.
*edit: Ik heb wel een document gevonden uit 2014, waar ik het in gelezen heb. Maar mijn vraag blijft staan: is dit nou wel / niet toegestaan op de huidige eindexamens
Dit bedoel ik met bussom: als je bij het berekenen van een driehoek opschrijft:
Opp driehoek ABC = 5 * 2 = 10 / 2 = 5 vierkante centimeter.
Ik tel het altijd fout, maar ik wil best even voor je opzoeken of dat volgens het nakijkmodel van het laatste examen terecht is.
-edit-
in het nakijkmodel staat de volgende tekst:Op basis daarvan zou men concluderen dat je je berekening zo mag opschrijven zonder dat het je punten kost.quote:Als in een berekening een notatiefout is gemaakt en als gezien kan worden dat de
kandidaat juist gerekend heeft, wordt hiervoor geen scorepunt afgetrokken.Opinion is the medium between knowledge and ignorance (Plato)
 Waarom doe je het niet gewoon op de juiste manier?quote:
Waarom doe je het niet gewoon op de juiste manier?quote:Op dinsdag 11 oktober 2016 15:31 schreef Silverdigger2 het volgende:
Kan iemand mij vertellen of bussommen op het wiskunde eindexamen van vmbo gl/tl fout worden gerekend? Ik kan mij herinneren dat ik dit een keer ergens gelezen heb maar kan dit niet terug vinden.
*edit: Ik heb wel een document gevonden uit 2014, waar ik het in gelezen heb. Maar mijn vraag blijft staan: is dit nou wel / niet toegestaan op de huidige eindexamens
Dit bedoel ik met bussom: als je bij het berekenen van een driehoek opschrijft:
Opp driehoek ABC = 5 * 2 = 10 / 2 = 5 vierkante centimeter.
 Los van alle discussies of het nu wel of niet fout gerekend zal worden is en blijft het gewoon fout. Het =-teken staat voor is gelijk aan en als hetgeen links en rechts van dit teken staat niet hetzelfde representeert, dan is je berekening fout, ongeacht de juistheid van het eindantwoord. Ik zag hier vroeger ook vaak mensen die het =-teken misbruikten als vervanging voor de werkwoordsvorm is in een uitspraak, en ook dat is fout.quote:
Los van alle discussies of het nu wel of niet fout gerekend zal worden is en blijft het gewoon fout. Het =-teken staat voor is gelijk aan en als hetgeen links en rechts van dit teken staat niet hetzelfde representeert, dan is je berekening fout, ongeacht de juistheid van het eindantwoord. Ik zag hier vroeger ook vaak mensen die het =-teken misbruikten als vervanging voor de werkwoordsvorm is in een uitspraak, en ook dat is fout.quote:Op dinsdag 11 oktober 2016 15:31 schreef Silverdigger2 het volgende:
Kan iemand mij vertellen of bussommen op het wiskunde eindexamen van vmbo gl/tl fout worden gerekend? Ik kan mij herinneren dat ik dit een keer ergens gelezen heb maar kan dit niet terug vinden.
*edit: Ik heb wel een document gevonden uit 2014, waar ik het in gelezen heb. Maar mijn vraag blijft staan: is dit nou wel / niet toegestaan op de huidige eindexamens
Dit bedoel ik met bussom: als je bij het berekenen van een driehoek opschrijft:
Opp driehoek ABC = 5 * 2 = 10 / 2 = 5 vierkante centimeter.
Maar, als je nu weet dat het fout is, waarom zou je het dan überhaupt nog zo op willen schrijven? Het is echt geen moeite om hier bijvoorbeeld ½ * 5 * 2 = 5 op te schrijven.
 *dit zijn niet echt vragen over het huiswerk, dus als dit offtopic is dan zal ik hier niet meer over doorgaan
*dit zijn niet echt vragen over het huiswerk, dus als dit offtopic is dan zal ik hier niet meer over doorgaan
Ik vind zelf dat je dit op het examen fout kan/moet rekenen. Dat het fout is snap ik, alleen als het de leerling toch geen punten kost... en als je de leerlingen klaar stoomt voor het examen...
Het kost je op het examen dus geen punten. Is het eindexamen nakijkmodel dan te soepel, of zijn de docenten op schoolexamens te streng?
 Jongens, ik zit met een vraag.
Jongens, ik zit met een vraag.
Je leent 5.000 euro bij de bank
Gedurende 10 jaar terug betalen aan het einde van het
jaar
De rente i = 6%
Hoe groot is het jaarlijkse bedrag dat je moet betalen?
Als ik dit invoer: 5000/(1-1.06-^10)/(0 .06) kom ik op het foute antwoord uit.
Weet iemand wat ik fout doe bij de invoer?Man is de baas, vrouw kent haar plaats.
 Gebruik (5000*0,06)/(1-1,06^-10)quote:
Gebruik (5000*0,06)/(1-1,06^-10)quote:Op donderdag 20 oktober 2016 17:29 schreef phpmystyle het volgende:
Jongens, ik zit met een vraag.
Je leent 5.000 euro bij de bank
Gedurende 10 jaar terug betalen aan het einde van het
jaar
De rente i = 6%
Hoe groot is het jaarlijkse bedrag dat je moet betalen?
Als ik dit invoer: 5000/(1-1.06-^10)/(0 .06) kom ik op het foute antwoord uit.
Weet iemand wat ik fout doe bij de invoer?
 Thanks. En weet jij ook hoe je dat doet bij prenummerando?quote:
Thanks. En weet jij ook hoe je dat doet bij prenummerando?quote:Op donderdag 20 oktober 2016 18:08 schreef lyolyrc het volgende:
[..]
Gebruik (5000*0,06)/(1-1,06^-10)Man is de baas, vrouw kent haar plaats.
 Nee, ik moest opzoeken wat prenumerando was, dus laat staan dat ik daarvoor berekeningen kan doen.quote:
Nee, ik moest opzoeken wat prenumerando was, dus laat staan dat ik daarvoor berekeningen kan doen.quote:Op maandag 24 oktober 2016 14:33 schreef phpmystyle het volgende:
[..]
Thanks. En weet jij ook hoe je dat doet bij prenummerando?

 Met behulp van geometrische reeksen kan je proberen om op een directe formule uit te komen.quote:
Met behulp van geometrische reeksen kan je proberen om op een directe formule uit te komen.quote:Op maandag 24 oktober 2016 14:33 schreef phpmystyle het volgende:
[..]
Thanks. En weet jij ook hoe je dat doet bij prenummerando?
 Hello, ik heb een vraag.
Hello, ik heb een vraag.
Ik heb het volgende probleem:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
[ Bericht 2% gewijzigd door jevl op 30-11-2016 08:06:18 ]
 quote:
quote:Op dinsdag 29 november 2016 12:41 schreef jevl het volgende:
Hello, ik heb een vraag.
Ik heb het volgende probleem:Je hebt een bepaald horizontale afstand X die je door de turbulentie vliegt. Dan is je totale verbuik:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Een vliegtuig vliegt een bepaalt pad van A naar B. Op de horizontale lijn Cb is de consumptie van het vliegtuig minimaal. Het gebied onder deze lijn (Ca) is turbulent; het verbruik is groter.
Nu moet ik de waarde van h en l bepalen waarbij het brandstofverbruik minimaal is.
Dit zal ongetwijfeld met differentiëren moeten, maar kom er niet uit. De waarden van Ca, Cb, l en h zijn constant.
Sqrt(h^2+X^2)*Ca + (L-X)*Cb
Dit moet je differentieren naar X en kijken wanneer dit 0 is. Daar zit je minimum.
 quote:
quote:Op dinsdag 29 november 2016 13:03 schreef jatochneetoch het volgende:
[..]Bedankt voor je antwoord, dan krijg je dit?:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
(X*Ca)/(sqrt(h^2+X^2))-Cb
Verder uitwerken gaat vervolgens niet zonder de waarden van Ca en Cb?
 quote:
quote:Op woensdag 30 november 2016 08:27 schreef jevl het volgende:
[..]
Bedankt voor je antwoord, dan krijg je dit?:
(X*Ca)/(sqrt(h^2+X^2))-Cb
Verder uitwerken gaat vervolgens niet zonder de waarden van Ca en Cb?
EDIT:
Mijn Latex code doet het helaas niet, iemand die weet waarom?
Edit: fixed door LB op aanraden van Riparius.
[ Bericht 5% gewijzigd door Lyrebird op 22-03-2017 08:05:16 ]

Hier staat die: https://latex.codecogs.com/gif.latex?\frac{XC_{a}}{\sqrt{h^{2}+X^{2}}}-C_{b}=0\\&space;XC_{a}-C_{b}\sqrt{h^{2}+X^{2}}=0\\&space;X^{2}C_{a}^{2}&space;-&space;C_{b}^{2}(h^{2}+X^{2})&space;=&space;0\\&space;(C_{a}^{2}-C_{b}^{2})X^{2}&space;-&space;C_{b}^{2}h^{2}&space;=&space;0\\&space;X^{2}&space;=&space;\frac{C_{b}^{2}h^{2}}{C_{a}^{2}-C_{b}^{2}}\\&space;X=&space;\sqrt{\frac{C_{b}^{2}h^{2}}{C_{a}^{2}-C_{b}^{2}}}
 Ja, je moet hier op FOK geen enter gebruiken tussen je TeX tags. Bedenk overigens dat je kunt schrijvenquote:
Ja, je moet hier op FOK geen enter gebruiken tussen je TeX tags. Bedenk overigens dat je kunt schrijvenquote:Op woensdag 30 november 2016 09:03 schreef jatochneetoch het volgende:
[..]
EDIT:
Mijn Latex code doet het helaas niet, iemand die weet waarom?
aangezien Ca > Cb > 0 en h > 0 terwijl X ook positief moet zijn.
 Je hebt kennelijk de opgave niet echt begrepen, want h en l zijn constantes en daarmee gegeven, want dus betekent dat er niets aan is te berekenen.quote:
Je hebt kennelijk de opgave niet echt begrepen, want h en l zijn constantes en daarmee gegeven, want dus betekent dat er niets aan is te berekenen.quote:Op dinsdag 29 november 2016 12:41 schreef jevl het volgende:
Nu moet ik de waarde van h en l bepalen waarbij het brandstofverbruik minimaal is.
Dit zal ongetwijfeld met differentiëren moeten, maar kom er niet uit. De waarden van Ca, Cb, l en h zijn constant.
Zoals eerder aangegeven kun je wel een uitdrukking afleiden voor het deel X van het gehele horizontale traject met lengte l waar het vliegtuig in een rechte lijn moet stijgen teneinde het brandstofverbruik te minimaliseren en daarvoor vonden we
Maar voor de piloot is het niet zo handig om deze waarde van X te kennen, de piloot is er juist in geïnteresseerd om te weten onder welke hoek met de horizontaal hij of zij het vliegtuig vanaf punt A moet laten stijgen teneinde het brandstofverbruik te minimaliseren. Welnu, laten we deze stijghoek α noemen, dan hebben we
zodat
De optimale stijghoek hangt dus uitsluitend af van het quotiënt van Ca en Cb. We kunnen deze uitdrukking nog vereenvoudigen met behulp van de goniometrische identiteit
en dan krijgen we
aangezien cos α positief is voor 0 < α < ½π en daarmee ook
[ Bericht 0% gewijzigd door Riparius op 03-12-2016 15:21:29 ]
 Postnumerando annuiteit delen door (1+i)quote:
Postnumerando annuiteit delen door (1+i)quote:Op maandag 24 oktober 2016 14:33 schreef phpmystyle het volgende:
[..]
Thanks. En weet jij ook hoe je dat doet bij prenummerando?
 Hey,
Hey,
Ik was een simulatie aan het programmeren, een eenvoudige Monte-Carlo simulatie van een Cramer-Lundberg model. Maw een verzekeringsmaatschappij waarbij premie, startkapitaal en stochastische claims worden gesimuleerd in een tijdsperiode. In het kort:
Aanname: arrivals are Poisson, claims sizes are Gamma distributed.
Mean claim size: 314 euro per claim
Mean arrival rate: 4.2 per day
De normale simulatie is gelukt. Nu moet ik het model aanpassen zodat de verwachte claims per week nog steeds 7*4.2 is maar in het weekend p% meer claims voorkomen dan doordeweeks.
Ik wilde dit zo programmeren:
double weekend = 5;
double parameter;
while(time < T){
double percentage = 0.1;
if(time % 7 < weekend){
parameter = 4.2*(percentage)*7/5;
}else{
parameter = 4.2*(1-percentage)*7/2;
}
arrivalTime = new ExponentialDistribution(1/parameter).sample();
Maar dit komt niet uit. Mijn logische fout (lijkt me) is dat ik nog steeds veronderstel dat een claim met kans 5/7 doordeweeks is, wat natuurlijk niet klopt als je aan die verhouding gaat rammelen. Nu kom ik er niet uit hoe ik die parameters wel moet definiëren.
Iemand die het verlossende lampje kan aanzetten?
De input van de Exponential lijkt niet te kloppen, echter gebruikt deze wiskunde API in Java als input het gemiddelde van de exponentiële verdeling, dus dit klopt wel.Fervent tegenstander van het korps lasergamers.
 Hoi,
Hoi,
Ik heb een vraag:
Stel dat je wilt weten of er een constante gemiddelde en constante variantie is waarbij dus E(Yt) = u en Var(Yt)= o², hoe kun je dit controleren? Moet je dan kijken naar de verschillen in lags? Dus bijvoorbeeld het gemiddelde en varianties voor time series van 1980-1960 en 2017-1981 en als er een verschil is concluderen dat het gemiddelde/de variantie niet constant is/zijn?
 Weet iemand hier toevallig hoe ik op de fx-9860GII de somrij tevoorschijn kan halen in het recursion menu? Ik krijg nu enkel de termen maar zie nergens een sigma of iets dergelijks en kan het bij SET ook niet vinden; ik vermoed dat het ergens anders buiten het recursion menu zit maar kan het niet vinden...
Weet iemand hier toevallig hoe ik op de fx-9860GII de somrij tevoorschijn kan halen in het recursion menu? Ik krijg nu enkel de termen maar zie nergens een sigma of iets dergelijks en kan het bij SET ook niet vinden; ik vermoed dat het ergens anders buiten het recursion menu zit maar kan het niet vinden...
Edit: al gevonden; het bleek via shift-menu in te stellen.
[ Bericht 5% gewijzigd door Consiliumpetens op 22-01-2017 23:33:57 ]
 Het uitwerkingsboekje heeft gelijk.quote:
Het uitwerkingsboekje heeft gelijk.quote:Op maandag 23 januari 2017 13:13 schreef Nelvalhil het volgende:
Iemand de mij even snel kan vertellen wat het domein is van
[ afbeelding ]
Ik zou zeggen [1; ->) Maar het uitwerkingsboekje komt uit op (0, 1]
1 kun je invullen, onder de wortel staat dan 0 en dat bestaat.
Alles tussen 0 en 1 kan ook (1/x is dan >1, en dus blijft er iets positiefs over onder de wortel)
0 kan uiteraard niet
Alles groter dan 1 levert een negatief getal onder de wortel op (bijv. 2: 1/2 - 1 = -1/2), en alles kleiner dan 0 ook
Netter geformuleerd: de formule heeft betekenis als 1/x-1 >= 0. Die ongelijkheid is niet al te ingewikkeld om op te lossen en komt uit op bovenstaande.Opinion is the medium between knowledge and ignorance (Plato)
 Ah, ik zat even helemáál verkeerd; dom dom dom.. Bedankt voor de uitlegquote:
Ah, ik zat even helemáál verkeerd; dom dom dom.. Bedankt voor de uitlegquote:Op maandag 23 januari 2017 13:23 schreef Janneke141 het volgende:
[..]
Het uitwerkingsboekje heeft gelijk.
1 kun je invullen, onder de wortel staat dan 0 en dat bestaat.
Alles tussen 0 en 1 kan ook (1/x is dan >1, en dus blijft er iets positiefs over onder de wortel)
0 kan uiteraard niet
Alles groter dan 1 levert een negatief getal onder de wortel op (bijv. 2: 1/2 - 1 = -1/2), en alles kleiner dan 0 ook
Netter geformuleerd: de formule heeft betekenis als 1/x-1 >= 0. Die ongelijkheid is niet al te ingewikkeld om op te lossen en komt uit op bovenstaande. 1 op de 6 mensen heeft 5 anderen om zich heen
1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers
 Hoi allen, ik had een korte vraag.
Hoi allen, ik had een korte vraag.
Het gaat over de vergelijking: ''ln(y) = a*x1 + b*x2''
Ik moet de relatie tussen y en x1 beschrijven.
Dit wordt in het antwoordmodel gedaan aan de hand van de afgeleide van de functie ln(y) naar x1, dus ''dln(y)/dx1 = a''. Tot zover begrijp ik het. Echter, hierna wordt de term ''dln(y)'' vervangen door ''dy/y''. Dit snap ik niet helemaal. Ik weet uiteraard dat de afgeleide van een functie ln(x) naar x gelijk is aan 1/x, maar toch snap ik niet waarom de term dln(y) vervangen mag worden door dy/y.
Ik hoop dat iemand dit kan toelichten. Bij voorbaat dank!
Edit: Ah laat maar, ik ben een idioot
Ik heb het antwoord al
[ Bericht 18% gewijzigd door ulq op 29-01-2017 22:00:43 ]
 Ik ben op het moment bezig mijn laatste propedeuse vak te behalen, calculus. Gaat me redelijk goed af maar ik mis het inzicht bij de volgende vraag:
Ik ben op het moment bezig mijn laatste propedeuse vak te behalen, calculus. Gaat me redelijk goed af maar ik mis het inzicht bij de volgende vraag:
http://imagizer.imageshack.us/v2/1024x768q90/922/VcQQZT.jpg (copy/paste deze link)
20.51 lukt mij redelijk. Als ik het goed begrijp gaat deze bij f(x) en g(x) van een 3e machts functie naar een 2e machts functie naar een 1e machts functie.
Maar vraag 20.52, iemand enig idee hoe je hier de juiste van elkaar afgeleide grafieken bij elkaar vind?
 Identificeer nulpunten, extrema en buigpunten in de grafieken.quote:
Identificeer nulpunten, extrema en buigpunten in de grafieken.quote:Op zaterdag 18 februari 2017 14:29 schreef KawaZ het volgende:
Ik ben op het moment bezig mijn laatste propedeuse vak te behalen, calculus. Gaat me redelijk goed af maar ik mis het inzicht bij de volgende vraag:
[ http://imagizer.imageshack.us/v2/1024x768q90/922/VcQQZT.jpg (copy/paste deze link) ]
20.51 lukt mij redelijk. Als ik het goed begrijp gaat deze bij f(x) en g(x) van een 3e machts functie naar een 2e machts functie naar een 1e machts functie.
Maar vraag 20.52, iemand enig idee hoe je hier de juiste van elkaar afgeleide grafieken bij elkaar vind?
Wat hebben deze met elkaar gemeen?
 Wat zijn de Engelse woorden voor termen als hoogtelijn, middellijn, koordenvierhoek, gelijkvormig, omgeschreven cirkel, etc? Ik kan het echt niet op internet vinden
Wat zijn de Engelse woorden voor termen als hoogtelijn, middellijn, koordenvierhoek, gelijkvormig, omgeschreven cirkel, etc? Ik kan het echt niet op internet vinden Hier schreef tong80 het volgende:
Hier schreef tong80 het volgende:
Faux is een FOK!held, zoals dat vroeger Gellarboy en Brechtje waren. Users die je koestert.
 Altitudequote:
Altitudequote:Op woensdag 8 maart 2017 23:51 schreef Faux. het volgende:
Wat zijn de Engelse woorden voor termen als hoogtelijn, middellijn, koordenvierhoek, gelijkvormig, omgeschreven cirkel, etc? Ik kan het echt niet op internet vinden
Diameter?
Cyclic quadrilateral
Similarity
Circumscribed circle
Tip; google '(nederlandse woord) wiskunde'
Dan evt wiki en naar engelse pagina
 Heldquote:
Heldquote:Op donderdag 9 maart 2017 00:12 schreef Frozen-assassin het volgende:
[..]
Altitude
Diameter?
Cyclic quadrilateral
Similarity
Circumscribed circle
Tip; google '(nederlandse woord) wiskunde'
Dan evt wiki en naar engelse pagina Hier schreef tong80 het volgende:
Hier schreef tong80 het volgende:
Faux is een FOK!held, zoals dat vroeger Gellarboy en Brechtje waren. Users die je koestert.
 Ik kom steeds op 0,18% uit
Ik kom steeds op 0,18% uit
Heb aantal per jaar uitgerekend van mannen en van vrouwen.
En daar uit gemiddelde ervan.
Wat doe ik fout? Juiste antwoord is A
[ Bericht 0% gewijzigd door beheerder01 op 12-03-2017 20:22:21 ]
 Het dikgedrukte.quote:
Het dikgedrukte.quote:Op zondag 12 maart 2017 20:16 schreef beheerder01 het volgende:
Ik kom steeds op 0,18% uit
Heb aantal per jaar uitgerekend van mannen en van vrouwen.
En daar uit gemiddelde ervan.
Wat doe ik fout? Juiste antwoord ja A
[ afbeelding ]
Het ziektepercentage van jaar 1 is (0,04*125+0,05*50)/175 * 100%.Opinion is the medium between knowledge and ignorance (Plato)
 Zie al waar het is misgegaan! Thanksquote:
Zie al waar het is misgegaan! Thanksquote:Op zondag 12 maart 2017 20:21 schreef Janneke141 het volgende:
[..]
Het dikgedrukte.
Het ziektepercentage van jaar 1 is (0,04*125+0,05*50)/175 * 100%.
 Heeft iemand hier verstand van MATLAB?
Heeft iemand hier verstand van MATLAB?
Ik wil namelijk een simpel 2D plotje maken, waarbij y een functie van x is met een sommatie. Voor die sommatie gebruik ik symsum. Verder is f(x) alleen afhankelijk van een paar vooraf vastgestelde parameters. Ik kies een range aan x-jes die ik er doorheen gooi om een mooie afbeelding te krijgen (x = 900:1:1000) Vervolgens gebruik ik de functie plot waarin ik x en y tegen elkaar afzet. Dit vindt ie echter niet leuk en hij zegt dat de waarden niet gedefinieerd zijn en de y waarden naar oneindig gaan.
https://nl.mathworks.com/help/matlab/ref/plot.html (deze dus)
Als ik echter mijn y-waarden los bereken door in de formule random x-jes te gooien komen er hele normale getallen uit (het betreft een kansverdeling, dus iets tussen 0 en 1).
Gebruik ik de verkeerde functies? Ik heb het idee dat ik iets ontzettend simpels mis, maar mijn zoektocht naar wat is vooralsnog niet geslaagdZodra ik zonder symsum ga werken lukt het allemaal wel, dus dat lijkt ervoor te zorgen dat hij het niet meer doet. Maar een oplossing zie ik zo snel niet.
[i]Put me on a pedestal and I'll only disappoint you
Tell me I'm exceptional and I promise to exploit you
Give me all your money and I'll make some origami honey
I think you're a joke but I don't find you very funny[/i]
 Is je y wel een vector? Eerst zeg je dat y een functie is daarna heb je het over f(x).quote:
Is je y wel een vector? Eerst zeg je dat y een functie is daarna heb je het over f(x).quote:Op vrijdag 17 maart 2017 00:11 schreef Mexicanobakker het volgende:
Heeft iemand hier verstand van MATLAB?
Ik wil namelijk een simpel 2D plotje maken, waarbij y een functie van x is met een sommatie. Voor die sommatie gebruik ik symsum. Verder is f(x) alleen afhankelijk van een paar vooraf vastgestelde parameters. Ik kies een range aan x-jes die ik er doorheen gooi om een mooie afbeelding te krijgen (x = 900:1:1000) Vervolgens gebruik ik de functie plot waarin ik x en y tegen elkaar afzet. Dit vindt ie echter niet leuk en hij zegt dat de waarden niet gedefinieerd zijn en de y waarden naar oneindig gaan.
https://nl.mathworks.com/help/matlab/ref/plot.html (deze dus)
Als ik echter mijn y-waarden los bereken door in de formule random x-jes te gooien komen er hele normale getallen uit (het betreft een kansverdeling, dus iets tussen 0 en 1).
Gebruik ik de verkeerde functies? Ik heb het idee dat ik iets ontzettend simpels mis, maar mijn zoektocht naar wat is vooralsnog niet geslaagdZodra ik zonder symsum ga werken lukt het allemaal wel, dus dat lijkt ervoor te zorgen dat hij het niet meer doet. Maar een oplossing zie ik zo snel niet.
Laat eens een voorbeeld zien doe niet werkt.
xs = 900:1:1000;
ys = arrayfun(y, xs);
plot(xs, ys);
Zoiets zou wel moeten werken als y een functie is.
[ Bericht 1% gewijzigd door t4rt4rus op 17-03-2017 00:43:24 ]
 Er werd bij deze som (Linaire Algebra) gevraagd om X,Y,Z uit te drukken in A en/of B
Er werd bij deze som (Linaire Algebra) gevraagd om X,Y,Z uit te drukken in A en/of B
Bij de laatste vergelijking [ 3) ] Kan er ook niet worden gesteld dat Z = -B/A ? Zo niet, waarom niet?1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers
 A en B hoeven niet te commuteren.quote:
A en B hoeven niet te commuteren.quote:Op vrijdag 31 maart 2017 19:15 schreef Nelvalhil het volgende:
Er werd bij deze som (Linaire Algebra) gevraagd om X,Y,Z uit te drukken in A en/of B
[ afbeelding ]
Bij de laatste vergelijking [ 3) ] Kan er ook niet worden gesteld dat Z = -B/A ? Zo niet, waarom niet?
 Sorry, maar hoezo kan dat dat evengoed niet?quote:
Sorry, maar hoezo kan dat dat evengoed niet?quote: 1 op de 6 mensen heeft 5 anderen om zich heen
1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers
 Matrix vermenigvuldiging is niet commutatief.quote:
Matrix vermenigvuldiging is niet commutatief.quote:Op vrijdag 31 maart 2017 20:12 schreef Nelvalhil het volgende:
[..]
Sorry, maar hoezo kan dat dat evengoed niet?
 Ja, natuurlijk! Dank je welquote:
Ja, natuurlijk! Dank je welquote:Op vrijdag 31 maart 2017 20:52 schreef t4rt4rus het volgende:
[..]
Matrix vermenigvuldiging is niet commutatief.Ik zat even buiten de matrix te denken; in vergelijkingen.
1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers
 Je kan niet delen door een matrixquote:
Je kan niet delen door een matrixquote:Op vrijdag 31 maart 2017 19:15 schreef Nelvalhil het volgende:
Er werd bij deze som (Linaire Algebra) gevraagd om X,Y,Z uit te drukken in A en/of B
[ afbeelding ]
Bij de laatste vergelijking [ 3) ] Kan er ook niet worden gesteld dat Z = -B/A ? Zo niet, waarom niet?

 Dat hangt natuurlijk compleet af van je definitie.quote:
Dat hangt natuurlijk compleet af van je definitie.quote:
Als delen de inverse van vermenigvuldigen is, kan je best het delen van matrices definiëren.
Als B inverteerbaar is
Net zoals je bij het delen van integers restricties hebt, heb je die dan bij het delen van matrices ook.
[ Bericht 1% gewijzigd door t4rt4rus op 03-04-2017 15:11:27 ]
 Hoi, ik heb een vraagje over die Heaviside step function. Ik heb een vergelijking
Hoi, ik heb een vraagje over die Heaviside step function. Ik heb een vergelijking
Waarbij Hz0 een constante is en H(t) de heaviside functie. Hier heb ik de afgeleide van nodig. Maar het lijkt mij gewoon dat dit 0 is, aangezien het in feite een horizontale lijn in vanaf een bepaald punt.
Iemand dit me hier kan helpen?leef de leven
 Nee sterretje moet gewoon 'keer' zijnquote:
Nee sterretje moet gewoon 'keer' zijnquote:Op zaterdag 8 april 2017 13:43 schreef thabit het volgende:
Staat * hier voor convolutie? Bedenk dat de afgeleide van H de Dirac delta is.
Thanks! Was even die naam kwijt, kan nu wel weer verder hoop ik leef de leven
leef de leven

Ik zou dit volgens mij moeten kunnen, maar ik kom gewoon niet uit (4) Prove that the matrix A only has one real number eigenvalue.
Ik vind
met karakteristieke vergelijking λ3 = λ2 + λ + 1
Ik weet dat er drie oplossingen zijn niet-reële oplossingen zijn, dus dat er één of drie reële oplossingen zijn. Ik heb alleen geen idee hoe ik kan laten zien dat er maar één reële oplossing is.
 Excuses zie dat ik een foutje heb gemaakt. Doe het nog even overnieuw.quote:
Excuses zie dat ik een foutje heb gemaakt. Doe het nog even overnieuw.quote:Op zaterdag 15 april 2017 12:28 schreef heyrenee het volgende:
[ afbeelding ]
Ik zou dit volgens mij moeten kunnen, maar ik kom gewoon niet uit (4) Prove that the matrix A only has one real number eigenvalue.
Ik vind
[ afbeelding ]
met karakteristieke vergelijking λ3 = λ2 + λ + 1
Ik weet dat er drie oplossingen zijn niet-reële oplossingen zijn, dus dat er één of drie reële oplossingen zijn. Ik heb alleen geen idee hoe ik kan laten zien dat er maar één reële oplossing is.
 Dit is uiteraard gewoon de karakteristieke vergelijking van je recursieve betrekking. Als je iets weet over kubische vergelijkingen is dit niet moeilijk. Herleiden op nul geeftquote:
Dit is uiteraard gewoon de karakteristieke vergelijking van je recursieve betrekking. Als je iets weet over kubische vergelijkingen is dit niet moeilijk. Herleiden op nul geeftquote:Op zaterdag 15 april 2017 12:28 schreef heyrenee het volgende:
Ik zou dit volgens mij moeten kunnen, maar ik kom gewoon niet uit (4) Prove that the matrix A only has one real number eigenvalue.
Ik vind
[ afbeelding ]
met karakteristieke vergelijking λ3 = λ2 + λ + 1
Ik weet dat er drie oplossingen zijn en dat niet-reële oplossingen toegevoegd complex zijn, dus dat er één of drie reële oplossingen zijn als er geen meervoudige wortels zijn. Ik heb alleen geen idee hoe ik kan laten zien dat er maar één reële oplossing is.
De som van de wortels van deze vergelijking is 1, dus als we een substitutie μ = λ − ⅓ oftewel λ = μ + ⅓ uitvoeren dan krijgen we een kubische vergelijking in μ waarvan de som van de wortels 0 is zodat de kwadratische term ontbreekt. Na herleiding heb je dan
Nu heeft een gereduceerde kubische vergelijking z3 + pz + q = 0 met reële coëfficiënten één reële en twee (toegevoegd) complexe wortels als de discriminant (p/3)3 + (q/2)2 positief is, en aangezien (−4/9)3 + (−38/54)2 = 11/27 heeft bovenstaande vergelijking in μ en daarmee ook je vergelijking in λ dus inderdaad één reële wortel.
Een andere manier is om het linkerlid van je vergelijking in λ herleid op 0 op te vatten als een functie van λ en te kijken naar de eerste afgeleide
Welnu, de eerste afgeleide heeft twee nulpunten λ = −1/3 en λ = 1, en met behulp van de tweede afgeleide
stel je dan vast dat de uitdrukking
een locaal maximum van −22/27 aanneemt voor λ = −1/3 en een locaal minimum van −2 voor λ = 1. Beide locale extrema hebben hetzelfde teken (ze zijn beide negatief) en daaruit volgt inderdaad weer dat bovenstaande uitdrukking in λ slechts één reëel nulpunt kan hebben.
[ Bericht 1% gewijzigd door Riparius op 15-04-2017 15:19:53 ]
Forum Opties Forumhop: Hop naar:




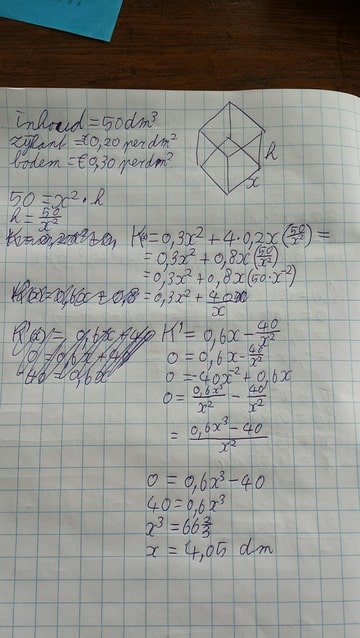














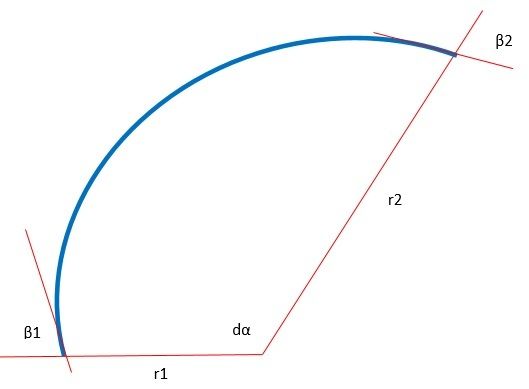
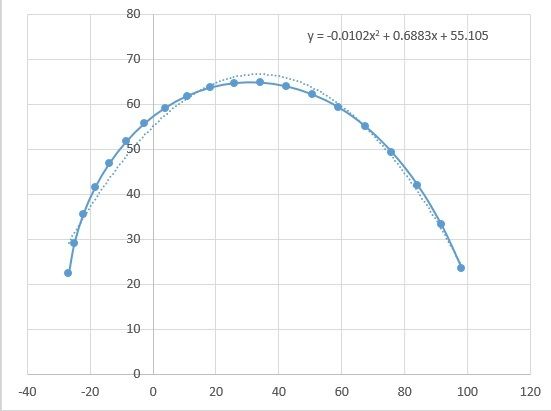

 Op
Op