SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
[ Bericht 98% gewijzigd door motorbloempje op 13-12-2015 19:13:34 ]
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
[ Bericht 98% gewijzigd door motorbloempje op 13-12-2015 19:13:34 ]
Ja doei.


Ik ben opzoek naar iemand die bijles kan geven met wiskunde b niveau
Zit in mijn propedeuse omgeving zuid Holland
Iemand tips ??
Zit in mijn propedeuse omgeving zuid Holland
Iemand tips ??


Niet hier. Aanbieden van of vragen om betaalde diensten is niet toegestaan op FOK. Je kunt hier uiteraard wel vragen stellen over opgaven of over 'theorie' of concepten waar je moeite mee hebt.quote:Op zondag 13 december 2015 15:01 schreef klawie het volgende:
Ik ben opzoek naar iemand die bijles kan geven met wiskunde b niveau
Zit in mijn propedeuse omgeving zuid Holland
Iemand tips ??


Je mag best vragen of iemand toevallig ervaring heeft met Studiehulp in een bepaalde regio. Je eigen diensten aanbieden of direct iemand vragen mag niet.
Ja doei.


ik zou eens kijken of er studenten aan je lokale universiteit te vinden zijn bij de exacte studies die bijles aanbieden? Even navragen bij de studievereniging van bijvoorbeeld wiskunde/informatica/natuurkunde ofzo.quote:Op zondag 13 december 2015 15:01 schreef klawie het volgende:
Ik ben opzoek naar iemand die bijles kan geven met wiskunde b niveau
Zit in mijn propedeuse omgeving zuid Holland
Iemand tips ??
Ja doei.


Op school had ik het al nagevraagd en ik ik zit niet bij een studenten corp
Maar ging mij meer of iemand toevallig goeie ervaringen had met iets of iemand
Maar ging mij meer of iemand toevallig goeie ervaringen had met iets of iemand


Jij hoeft toch niet bij een 'corp'(? Wat heeft dat met een studievereniging te maken?) te zitten om bij een andere studievereniging te vragen of zij mensen kennen die bijles geven?
Ja doei.


Weet iemand hoe ik de volgende formule kan differentiëren naar: d σ² / d xa ?
σ² = 0,06² *xa² + 0,04² * (1-xa)² + 2*xa * (1-xa) * 0,5*0,04*0,06
Ik moet uitkomen op 0,0056xa - 0,0008.
Hoe ik de tweede en derde term moet differentiëren ben ik een tikkeltje vergeten. Ik wou voor het gemak even allereerst alles netjes uitschrijven, maar toen kwam ik uit op :
0,0012xa² - 0,0032(1-xa) + 0,0024xa
Maar dat moet fout zijn, aangezien uitschrijven het volgende moet opleveren:
Ik ben dus benieuwd naar de methodiek van zo snel mogelijk differentiëren (zonder uitschrijven) en naar de uitschrijfmethodiek.
σ² = 0,06² *xa² + 0,04² * (1-xa)² + 2*xa * (1-xa) * 0,5*0,04*0,06
Ik moet uitkomen op 0,0056xa - 0,0008.
Hoe ik de tweede en derde term moet differentiëren ben ik een tikkeltje vergeten. Ik wou voor het gemak even allereerst alles netjes uitschrijven, maar toen kwam ik uit op :
0,0012xa² - 0,0032(1-xa) + 0,0024xa
Maar dat moet fout zijn, aangezien uitschrijven het volgende moet opleveren:
Ik ben dus benieuwd naar de methodiek van zo snel mogelijk differentiëren (zonder uitschrijven) en naar de uitschrijfmethodiek.


Het kan inderdaad door uitschrijven, of door het gebruiken van de produkt- en kettingregel. Als je daarbij niet uitkomt op het goede antwoord, is de meest voor de hand liggende optie dat je bij al die nare getallen ergens een rekenfoutje hebt gemaakt.
0,06² *xa² + 0,04² * (1-xa)² + 2*xa * (1-xa) * 0,5*0,04*0,06
=
0,0036xa² + 0,0016(1-xa)² + 0,0024xa(1-xa)
=
0,0036xa² + 0,0016 (1-2xa+xa²) + 0,0024(xa-xa²)
=
0,0036xa² + 0,0016 - 0,0032xa + 0,0016xa² + 0,0024xa - 0,0024xa²
=
0,0028xa² - 0,0008xa + 0,0016
Check.
0,06² *xa² + 0,04² * (1-xa)² + 2*xa * (1-xa) * 0,5*0,04*0,06
=
0,0036xa² + 0,0016(1-xa)² + 0,0024xa(1-xa)
=
0,0036xa² + 0,0016 (1-2xa+xa²) + 0,0024(xa-xa²)
=
0,0036xa² + 0,0016 - 0,0032xa + 0,0016xa² + 0,0024xa - 0,0024xa²
=
0,0028xa² - 0,0008xa + 0,0016
Check.
Opinion is the medium between knowledge and ignorance (Plato)


Op die fiets dacht dat je bij een corp moest zitten om gebruik te maken van die diensten zeg maarquote:Op zondag 13 december 2015 20:05 schreef motorbloempje het volgende:
Jij hoeft toch niet bij een 'corp'(? Wat heeft dat met een studievereniging te maken?) te zitten om bij een andere studievereniging te vragen of zij mensen kennen die bijles geven?
Maar por morgen een aantal mensen in hun zij top!


Dat is onbegrijpelijk, want je hebt de bekende regels voor het differentiëren toch geleerd en er ook tentamen in gedaan?quote:Op zondag 13 december 2015 20:47 schreef RustCohle het volgende:
Weet iemand hoe ik de volgende formule kan differentiëren naar d σ² / d xa xA?
σ² = 0,06² *xA² + 0,04² * (1-xA)² + 2*xA * (1-xA) * 0,5*0,04*0,06
Ik moet uitkomen op 0,0056xA - 0,0008.
Hoe ik de tweede en derde term moet differentiëren ben ik een tikkeltje vergeten.
Hier is dat nog gemakkelijk te doen, maar stel dat er een term met (1−xA)10 in je uitdrukking had gezeten, dan is uitschrijven niet goed meer te doen terwijl direct differentiëren nog even gemakkelijk is. Geen goed plan dus.quote:Ik wou voor het gemak even allereerst alles netjes uitschrijven,
Ik heb eens even naar de uitdrukking zitten kijken die je zelf had gevonden om te zien hoe je daar op bent gekomen, en dat is mij helaas maar al te duidelijk geworden.quote:maar toen kwam ik uit op :
0,0012xA² - 0,0032(1-xA) + 0,0024xA
Maar dat moet fout zijn, aangezien uitschrijven het volgende moet opleveren:
[ afbeelding ]
Je bent kennelijk begonnen met 0,06²·xA² = 0,0036·xA² en je hebt daar 2·xA·xA·0,5·0,04·0,06 = 0,0024·xA² uit de derde term vanaf getrokken om op 0,0012·xA² uit te komen. Maar dat impliceert dat je helemaal niet hebt gezien dat
0,04²·(1−xA)²
ook nog eens een term 0,0016·xA² oplevert bij uitwerken, zodat we 0,0012·xA² + 0,0016·xA² = 0,0028·xA² krijgen.
Kennelijk verkeer je in de veronderstelling dat 0,04²·(1−xA)² hetzelfde zou zijn als
0,0032·(1−xA)
want dat is de tweede term in je uitwerking. Je kent dus na meer dan een jaar nog steeds niet je merkwaardige producten. En dan ben je ook nog vergeten dat uitwerken van de haakjes van de derde term behalve een kwadratische term ook nog een lineaire term oplevert.
Er zit niets anders op dan de regels voor het differentiëren en voor het uitvoeren van algebraïsche herleidingen te blijven oefenen, net zolang totdat je ze vlot en foutloos uit kunt voeren. Voor deze opgave kun je je trouwens foutgevoelige berekeningen met die decimale breuken besparen door eerst even een factor 10−4 buiten haakjes te halen, dan krijg jequote:Ik ben dus benieuwd naar de methodiek van zo snel mogelijk differentiëren (zonder uitschrijven) en naar de uitschrijfmethodiek.
differentiëren naar xA geeft dan


Dit convergeert naar
(De gehele vraag is om aan te tonen


Een oneindig product waarvan elke factor uit een som van twee termen bestaat is lastig te hanteren, dus het idee is om deze som om te zetten in een product zodat we het oneindige product om kunnen zetten in een product van oneindige producten die elk afzonderlijk beter zijn te hanteren. Je kuntquote:Op dinsdag 15 december 2015 11:16 schreef Novermars het volgende:
Dit convergeert naar, maar iemand enig idee hoe dit aan te tonen?
herschrijven als
en dan bij
een factor
buiten haakjes halen, zodat we krijgen
oftewel
en daarmee
Het eerste van deze oneindige producten is gemakkelijk te bepalen, aangezien exponenten optellen bij vermenigvuldiging van machten van hetzelfde grondtal, zodat dit neerkomt op het sommeren van een oneindige meetkundige reeks met reden ½, die uiteraard convergeert.
Voor het tweede oneindige product kun je gebruik maken van het bekende resultaat
waarvan je hier een eenvoudig bewijs kunt vinden.
Een oneindige meetkundige reeks met als eerste term ¼it en met als reden ½ heeft als som ½it, dus hebben we
en verder hebben we (voor t ≠ 0)
zodat je oneindige product dus convergeert naar
QED
[ Bericht 1% gewijzigd door Riparius op 18-12-2015 02:58:01 ]


Mijn complimenten, ik was er zelf niet opgekomen om de som in een product om te zetten. Ik zocht wel in de richting van goniometrische functies, maar was de sinc identity nog niet tegen gekomen, in het vervolg misschien ook maar in het Duits googelen!quote:
Bedankt!


Ik heb soms moeite met het snappen van de notatie, neem bijvoorbeeld dit stukje: https://www.dropbox.com/s(...)%2017-03-36.png?dl=0
Wat wordt er bijvoorbeeld bedoeld met 'beschouw voor elke n in N de verzameling B_n ...'?
Heeft iemand tips om de notatie beter te snappen?
Wat wordt er bijvoorbeeld bedoeld met 'beschouw voor elke n in N de verzameling B_n ...'?
Heeft iemand tips om de notatie beter te snappen?


Ze definiëren Bn := (0, n] voor elke n ∈ ℕ zodat elke Bn dus een half open half gesloten interval is op ℝ. Een interval op ℝ is een verzameling reële getallen zodat elke Bn dus een deelverzameling is van ℝ. Heb je wel eens wat over verzamelingenleer en de daarbij gebruikte notaties gehad op school?quote:Op maandag 21 december 2015 17:05 schreef netchip het volgende:
Ik heb soms moeite met het snappen van de notatie, neem bijvoorbeeld dit stukje: https://www.dropbox.com/s(...)%2017-03-36.png?dl=0
Wat wordt er bijvoorbeeld bedoeld met 'beschouw voor elke n in N de verzameling B_n ...'?
Heeft iemand tips om de notatie beter te snappen?


Waarom is U_n ∈ ℕ B_n = (0, oneindig)? Stel dat we n = 5 kiezen, dan krijgen we toch (0, 5] en toch geen (0, oneindig)?quote:Op maandag 21 december 2015 17:17 schreef Riparius het volgende:
[..]
Ze definiëren Bn := (0, n] voor elke n ∈ ℕ zodat elke Bn dus een half open half gesloten interval is op ℝ. Een interval op ℝ is een verzameling reële getallen zodat elke Bn dus een deelverzameling is van ℝ. Heb je wel eens wat over verzamelingenleer en de daarbij gebruikte notaties gehad op school?
Verzamelingenleer heb ik niet gehad op school, ik doe dit in m'n vrije tijd.


Het gaat hier over de vereniging (Engels: union) van alle verzamelingen Bn met n ∈ ℕ. En die vereniging bestaat uit alle positieve reële getallen.quote:Op maandag 21 december 2015 17:48 schreef netchip het volgende:
[..]
Waarom is U_n ∈ ℕ B_n = (0, oneindig)? Stel dat we n = 5 kiezen, dan krijgen we toch (0, 5] en toch geen (0, oneindig)?
Begin eens even met dit artikel en ook dit artikel in Wikipedia.quote:Verzamelingenleer heb ik niet gehad op school, ik doe dit in m'n vrije tijd.


Ik heb een paar korte vragen over encryptie.
Ik begrijp wat encryptie met behulp van een rotatie is (Caesar), namelijk gewoon alle letters een aantal posities opgeschoven. Ik meen me te herinneren dat je dat kunt schrijven als
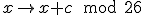
Maar dit ontcijferen is zeer eenvoudig.
Een ietwat meer geavanceerde encryptiemethode is
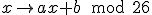
Ik geloof dat deze encryptie bekend is onder de naam Vigenère, klopt dat?
En klopt het dat je de sleutel (de natuurlijke getallen a en b) kunt verkrijgen als je van twee letters weet op welke letters zij worden afgebeeld?
Mijn derde vraag gaat over de volgende encryptiemethode waarbij het alfabet wordt gegeven door:
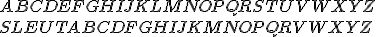
Oftewel dat de eerste letters worden afgebeeld op een sleutelwoord (hier: sleutel) en de overige letters staan op alfabetische volgorde.
Ik ben benieuwd hoe deze encryptiemethode heet (ik wil er graag meer over weten), en hoe goed is deze encryptymethode?
Ik begrijp wat encryptie met behulp van een rotatie is (Caesar), namelijk gewoon alle letters een aantal posities opgeschoven. Ik meen me te herinneren dat je dat kunt schrijven als
Maar dit ontcijferen is zeer eenvoudig.
Een ietwat meer geavanceerde encryptiemethode is
Ik geloof dat deze encryptie bekend is onder de naam Vigenère, klopt dat?
En klopt het dat je de sleutel (de natuurlijke getallen a en b) kunt verkrijgen als je van twee letters weet op welke letters zij worden afgebeeld?
Mijn derde vraag gaat over de volgende encryptiemethode waarbij het alfabet wordt gegeven door:
Oftewel dat de eerste letters worden afgebeeld op een sleutelwoord (hier: sleutel) en de overige letters staan op alfabetische volgorde.
Ik ben benieuwd hoe deze encryptiemethode heet (ik wil er graag meer over weten), en hoe goed is deze encryptymethode?


Het is inderdaad een kwestie van proberen van wat getallen, als je er twee weet.quote:Op zaterdag 26 december 2015 17:18 schreef mr.wout het volgende:
Ik heb een paar korte vragen over encryptie.
Ik begrijp wat encryptie met behulp van een rotatie is (Caesar), namelijk gewoon alle letters een aantal posities opgeschoven. Ik meen me te herinneren dat je dat kunt schrijven als
Maar dit ontcijferen is zeer eenvoudig.
Een ietwat meer geavanceerde encryptiemethode is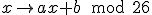
Ik geloof dat deze encryptie bekend is onder de naam Vigenère, klopt dat?
En klopt het dat je de sleutel (de natuurlijke getallen a en b) kunt verkrijgen als je van twee letters weet op welke letters zij worden afgebeeld?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.


Integreren over snelheid v(x) geeft de afstand over een tijd.
Wat geeft integreren over acceleratie a(x) en integreren over f(x)?
Bedankt alvast!
Wat geeft integreren over acceleratie a(x) en integreren over f(x)?
Bedankt alvast!


Je moet nog maar eens goed in je wis- en natuurkundeboeken bladeren om na te kijken hoe je dit precies moet formuleren, want dit verdient niet direct de schoonheidsprijs.quote:Op dinsdag 5 januari 2016 16:16 schreef obsama het volgende:
Integreren over snelheid v(x) geeft de afstand over een tijd.
Wat geeft integreren over acceleratie a(x) en integreren over f(x)?
Bedankt alvast!
Maar wat je waarschijnlijk wil weten is dat het integreren van de acceleratie normaal gesproken de snelheid oplevert. Echter, net zo normaal gesproken zijn dat allemaal functies met de tijd (t) als variabele, en niet x (afstand).
v(t) = x'(t), a(t) = v'(t)
En wat f(x) zou betekenen staat niet in je post. In zijn algemeenheid gebruik je het integreren van f(x) om de oppervlakte onder de grafiek van f te bepalen. Wat die uitkomst betekent, is geheel afhankelijk van je context.
Opinion is the medium between knowledge and ignorance (Plato)


Ja sorry wat te snel verwoord. Wat ik bedoel is het volgende:quote:Op dinsdag 5 januari 2016 16:50 schreef Janneke141 het volgende:
[..]
Je moet nog maar eens goed in je wis- en natuurkundeboeken bladeren om na te kijken hoe je dit precies moet formuleren, want dit verdient niet direct de schoonheidsprijs.
Maar wat je waarschijnlijk wil weten is dat het integreren van de acceleratie normaal gesproken de snelheid oplevert. Echter, net zo normaal gesproken zijn dat allemaal functies met de tijd (t) als variabele, en niet x (afstand).
v(t) = x'(t), a(t) = v'(t)
En wat f(x) zou betekenen staat niet in je post. In zijn algemeenheid gebruik je het integreren van f(x) om de oppervlakte onder de grafiek van f te bepalen. Wat die uitkomst betekent, is geheel afhankelijk van je context.
Als ik de integraal tussen t1=0 en t2=5 neem van v(x) en de eenheid is meter per seconde dan is de uitkomst toch gewoon de afstand die ik heb afgelegd tussen t1 en t2 in meters per seconde?
Wat nou als ik de integraal neem van t1=0 en t2=5 van a(x), wat stelt het getal dat daar uitkomt dan voor?
Sorry voor het houtje touwtje bericht, ik hoop dat het zo iets duidelijker is.


Waarom volg je mijn tip niet op en gebruik je de tijd t als variabele? Je maakt jezelf nogal in de war door dat niet te doen.quote:Op dinsdag 5 januari 2016 16:57 schreef obsama het volgende:
[..]
Ja sorry wat te snel verwoord. Wat ik bedoel is het volgende:
Als ik de integraal tussen t1=0 en t2=5 neem van v(x) en de eenheid is meter per seconde dan is de uitkomst toch gewoon de afstand die ik heb afgelegd tussen t1 en t2 in meters per seconde?
Wat nou als ik de integraal neem van t1=0 en t2=5 van a(x), wat stelt het getal dat daar uitkomt dan voor?
Sorry voor het houtje touwtje bericht, ik hoop dat het zo iets duidelijker is.
Het levert je als uitkomst niet de gemiddelde snelheid tussen t1 en t2
[ Bericht 5% gewijzigd door Janneke141 op 05-01-2016 17:46:33 ]
Opinion is the medium between knowledge and ignorance (Plato)


Nee, want ½(v(t1) + v(t2)) is in het algemeen iets anders dan v(t2) − v(t1).quote:Op dinsdag 5 januari 2016 16:57 schreef Janneke141 het volgende:
[..]
Het levert je als uitkomst de gemiddelde snelheid tussen t1 en t2.

