[Bèta wiskunde] Huiswerk- en vragentopic.

quote:

Op maandag 7 september 2015 11:40 schreef Super-B het volgende:
Goedemorgen,

Ik heb een vraag omtrent de 'inverse'. Zojuist heb ik de MPLc (marginal product of labor in cars) berekend. Er wordt beweerd dat als je de productie van auto's wilt uitbreiden met 1 unit, dat je dan de labor input met 1/MPLc uren moet verhogen.

[ afbeelding ]

Wat zegt de inverse van MPLc dan eigenlijk? Waarom neem je überhaupt 1/MPLc?

P.S; dit soort dingen tref ik overigens wel vaker:

[ afbeelding ]

Hierbij snap ik wiskunde technisch wel hoe je op 1/ ALc komt (ALc = labor requirement, w = wage, Pc= prijs van kaas). Ook snap ik dat als je het loon deelt door de prijs van kaas dat je weet hoeveel kaas je kunt kopen. Desondanks begrijp ik praktisch gezien niet (wiskundig wel) waarom je met 1/ALc hetzelfde kunt berekenen? Waarom die 1/..? 1/aantal labor? Weer zo'n inverse...

Schrijf de betrekking



eens als



dan zie je wellicht beter dat Q_c (het aantal geproduceerde auto's) kwadratisch afhangt van L_c (de hoeveelheid arbeid die wordt geïnvesteerd om die auto's te produceren). Dit is in feite een differentiaalvergelijking en als je als beginvoorwaarde aanneemt Q_c = 0 voor L_c = 0 (immers: zonder arbeid zul je geen auto's produceren) dan krijg je als oplossing voor deze differentiaalvergelijking



Nu zijn L_c en Q_c hier wiskundig gezien reële grootheden waarbij Q_c continu afhangt van L_c maar in de praktijk is in ieder geval Q_c een discrete grootheid (je produceert een geheel aantal auto's), zodat dit (eenvoudige) wiskundige model maar in beperkte mate een economische realiteit weerspiegelt.

Maar je ziet wel dat de kwadratische relatie tussen de hoeveelheid arbeid en de aantallen geproduceerde auto's impliceert dat naarmate het aantal geproduceerde auto's hoger ligt er steeds minder extra arbeid nodig is om nog één extra auto te produceren (schaalvergroting maakt de productie efficiënter). Dat kun je ook mooi zien als je een grafiek tekent van bovenstaande relatie tussen Q_c en L_c. De grafiek van Q_c als functie van L_c is een (halve) dalparabool, en je ziet dat deze steeds steiler gaat lopen naarmate L_c groter wordt. In feite is de steilheid van (de raaklijn aan) de parabool in ieder punt recht evenredig met L_c.

Een differentiaalquotiënt is niets anders dan een limiet van een differentiequotiënt en zo hebben we hier



Voor kleine waarden van ΔL_c is het differentiaalquotiënt dQc/dLc bij benadering gelijk aan het differentiequotiënt ΔQ_c/ΔL_c zodat we dus ook bij benadering hebben



en daarmee ook



Als nu het aantal geproduceerde auto's met één toeneemt, dus ΔQ_c = 1, dan hebben we zo



waaruit volgt dat



De hoeveelheid extra arbeid ΔL_c benodigd om nog één extra auto te produceren (ΔQ_c = 1) is hier dus inderdaad omgekeerd evenredig met de reeds geïnvesteerde hoeveelheid arbeid L_c.

[ Bericht 0% gewijzigd door Riparius op 07-09-2015 16:41:49 ]

Statistici onder ons:

Let q be an unbiased estimator of p. Proof that q² is a biased estimator of p².

Nu volgens mij komt dat neer op aantonen dat:

E[q²] - p² ≠ 0

Ik dacht dat:

E[q²] - p²
= E[q²-p²] (p is niet random toch?)
= E[(q-p)(p+q)]
= Cov((q-p),(p+q)) + E[q-p]E[p+q], deze laatste term is dan identiek 0.

Maar verder heb ik geen idee.


Cov(X,Y) := E[(X - E[X])(Y-E[Y])]

E[q-p] = 0 zodat:

Cov(q-p,p+q) = E[(q-p)(q+p-E[q] - p)]
= E[(q-p)(q-E[q])]


En daar loop ik een beetje vast. Iemand?

quote:

Op donderdag 10 september 2015 09:56 schreef Anoonumos het volgende:
Var q = E(q²) - (Eq)² = E(q²) - p²

en variantie is geen 0

denk ik

Ja dat idee had ik ook al, maar waarom?

Het wachten is op Thabit

quote:

Op donderdag 10 september 2015 11:08 schreef Anoonumos het volgende:

[..]

Waarom wat?

Die vergelijking is simpel en variantie is alleen 0 voor een degenerate distribution

Ik zei alleen 'denk ik' omdat ik nog half sliep ( ) maar het is wel simpel.

Ik vroeg mij af waarom ik mocht zeggen dat de variantie ongelijk 0 is. Maar okay! Ik ben niet zo'n held betreffende de kansrekening.

quote:

Op donderdag 10 september 2015 11:56 schreef Amoeba het volgende:

[..]

Ik vroeg mij af waarom ik mocht zeggen dat de variantie ongelijk 0 is. Maar okay! Ik ben niet zo'n held betreffende de kansrekening.

Als het een degenerate distribution is dan is de stelling gewoon niet waar.

Stel je hebt een verdeling gedefinieerd door P(X=2)=1, dan is 2 een unbiased estimator van X, en 2²=4 een unbiased estimator van X^2.

Als je aanneemt dat de verdeling niet degenerate is, dan kun je gebruiken dat Var X>0 (of equivalent, Jensen's ongelijkheid).

Hallo goedemiddag,

Tijdens het studeren ben ik iets in de war geraakt betreffende de richtingscoëfficiënt. Zo ver ik weet wordt het als volgt berekend:



Desondanks stuitte ik op iets verwarrends:





Ik zou juist denken aan: A*LW/ A*LC. Waarom is het hier anders?


Hier wordt namelijk wel de ´juiste´ methodiek toegepast (dY/dX):






De opportunity cost van 'manufactured goods' is, in mijn ogen, 100/10 = 10, waartegen dat in strijd is met de eerste twee afbeeldingen waarbij dX/dY wordt gedaan..(?)

Zou iemand het mij kunnen verklaren?

[ Bericht 2% gewijzigd door Super-B op 12-09-2015 13:58:23 ]

quote:

Op zaterdag 12 september 2015 13:52 schreef Super-B het volgende:
Hallo goedemiddag,

Tijdens het studeren ben ik iets in de war geraakt betreffende de richtingscoëfficiënt. Zo ver ik weet wordt het als volgt berekend:

[snip]

Zou iemand het mij kunnen verklaren?[/b]

Als je vroeger goed had leren rekenen met breuken dan had je direct gezien dat de absolute waarde van de richtingscoëfficiënt van de rechte door de punten P en F in je eerste plaatje gelijk is aan

(L/a_LW) / (L/a_LC) = a_LC / a_LW

quote:

Op dinsdag 22 september 2015 19:10 schreef d4v1d het volgende:
Kan je hier ook terecht met rekenvragen? ( )

Ik doe nu MBO, niv 3. Ik kan een jaar overslaan maar dan moet ik even eindtoetsen maken om van elk vak te laten zien dat ik niet een complete idioot ben. Ik kan opzich best rekenen (wiskunde iets minder, maar dat heb ik niet gelukkig) maar het is echt heel erg weggezakt. Ik moet dus weer wat theorie lezen en opdrachten maken. (Ik zou nu niet kunnen benoemen hoe je een breuk deelt. Bijvoorbeeld, maar dat heb ik dan ook een jaar of 2 niet meer gedaan.. )

Ik zoek dus eigenlijk een samenvatting voor niveau 2F rekenen, dan kan ik alle stof nog eens doorlezen. Ik zie het niet echt zitten om 2 rekenboeken van 2F door te nemen in een week

Hiermee geef je al aan dat je niet echt moeite wenst te doen.

Ik vind wel overheidspublicaties met de eisen, maar geen echte samenvattingen van de stof. Ga dus toch maar braaf die twee boeken doornemen die je kennelijk al hebt.

quote:

Ik hoef dus niet echt meer iets te leren (het niveau is echt droevig van dit rekenboek) Wil dus vooral stof herhalen en omhoog halen.

Hiermee spreek je jezelf tegen, want je hebt net gezegd dat de stof heel erg is weggezakt. Rekenen is net als fietsen: als je het eenmaal kunt, dan blijf je het je hele leven kunnen (zolang je tenminste nog fysiek en geestelijk in orde bent).

Hier vind je een voorbeeldtoets. Maak die om te kijken of je de stof beheerst. Als dat niet zo is dan heb je het nooit goed geleerd.

Stel dat ik deze functie vermenigvuldig met Q om de totale opbrengsten te krijgen, dan krijg ik dit:

TO = aQ/b - Q²/b

Als ik hiervan de marginale opbrengsten formule wil afleiden, moet ik d TO / dQ berekenen. Dat gebeurt als volgt:

dTO/dQ: a/b - 2Q/b

Klopt dit?

quote:

Op dinsdag 22 september 2015 21:25 schreef RustCohle het volgende:
[ afbeelding ]

Stel dat ik deze functie vermenigvuldig met Q om de totale opbrengsten te krijgen, dan krijg ik dit:

TO = aQ/b - Q²/b

Als ik hiervan de marginale opbrengsten formule wil afleiden, moet ik d TO / dQ berekenen. Dat gebeurt als volgt:

dTO/dQ: a/b - 2Q/b

Klopt dit?

Ja, dit klopt. Schrijf alleen liever d(TO)/dQ omdat TO hier één grootheid voorstelt (en niet het product van twee grootheden T en O).

quote:

Op donderdag 10 september 2015 20:34 schreef thenxero het volgende:

[..]

Als het een degenerate distribution is dan is de stelling gewoon niet waar.

Stel je hebt een verdeling gedefinieerd door P(X=2)=1, dan is 2 een unbiased estimator van X, en 2²=4 een unbiased estimator van X^2.

Als je aanneemt dat de verdeling niet degenerate is, dan kun je gebruiken dat Var X>0 (of equivalent, Jensen's ongelijkheid).

We kregen later een mailtje met de rectificatie. Je moet dan gebruiken dar Var(X) > 0 en dan 'if you are very picky' in dat mailtje. Nee flikker op, ik heb een half uur lopen zoeken naar een goed bewijs en dan kom je met deze onzin aanzetten

quote:

Op woensdag 23 september 2015 01:01 schreef Amoeba het volgende:

[..]

'if you are very picky'

Lees: 'if you are a mathematician'

quote:

Op woensdag 23 september 2015 11:12 schreef thenxero het volgende:

[..]

Lees: 'if you are a mathematician'

'
Ja precies. Ik vind uitspraken doen waarvan ik eigenlijk zeker weet dat ze niet per se waar zijn ook wel een dooddoener. Als je dan nog niet weet dat het bewijs eigenlijk niet waar is (ik was niet op de hoogte van de uitzondering van een degenerate distribution), dan blijf je rondjes lopen. Best vervelend om zo je tijd te moeten verspillen en dat je dan zo'n afgezaagd mailtje krijgt dat je 'picky' bent.

quote:

Op maandag 7 september 2015 16:06 schreef Riparius het volgende:

[..]

Schrijf de betrekking



eens als



dan zie je wellicht beter dat Q_c (het aantal geproduceerde auto's) kwadratisch afhangt van L_c (de hoeveelheid arbeid die wordt geïnvesteerd om die auto's te produceren). Dit is in feite een differentiaalvergelijking en als je als beginvoorwaarde aanneemt Q_c = 0 voor L_c = 0 (immers: zonder arbeid zul je geen auto's produceren) dan krijg je als oplossing voor deze differentiaalvergelijking



Nu zijn L_c en Q_c hier wiskundig gezien reële grootheden waarbij Q_c continu afhangt van L_c maar in de praktijk is in ieder geval Q_c een discrete grootheid (je produceert een geheel aantal auto's), zodat dit (eenvoudige) wiskundige model maar in beperkte mate een economische realiteit weerspiegelt.

Maar je ziet wel dat de kwadratische relatie tussen de hoeveelheid arbeid en de aantallen geproduceerde auto's impliceert dat naarmate het aantal geproduceerde auto's hoger ligt er steeds minder extra arbeid nodig is om nog één extra auto te produceren (schaalvergroting maakt de productie efficiënter). Dat kun je ook mooi zien als je een grafiek tekent van bovenstaande relatie tussen Q_c en L_c. De grafiek van Q_c als functie van L_c is een (halve) dalparabool, en je ziet dat deze steeds steiler gaat lopen naarmate L_c groter wordt. In feite is de steilheid van (de raaklijn aan) de parabool in ieder punt recht evenredig met L_c.

Een differentiaalquotiënt is niets anders dan een limiet van een differentiequotiënt en zo hebben we hier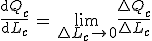



Voor kleine waarden van ΔL_c is het differentiaalquotiënt dQc/dLc bij benadering gelijk aan het differentiequotiënt ΔQ_c/ΔL_c zodat we dus ook bij benadering hebben



en daarmee ook



Als nu het aantal geproduceerde auto's met één toeneemt, dus ΔQ_c = 1, dan hebben we zo



waaruit volgt dat



De hoeveelheid extra arbeid ΔL_c benodigd om nog één extra auto te produceren (ΔQ_c = 1) is hier dus inderdaad omgekeerd evenredig met de reeds geïnvesteerde hoeveelheid arbeid L_c.

quote:

Op zaterdag 12 september 2015 16:21 schreef Riparius het volgende:

[..]

Als je vroeger goed had leren rekenen met breuken dan had je direct gezien dat de absolute waarde van de richtingscoëfficiënt van de rechte door de punten P en F in je eerste plaatje gelijk is aan

(L/a_LW) / (L/a_LC) = a_LC / a_LW

Bedankt voor je uitgebreide uitleg.

quote:

Op woensdag 23 september 2015 12:20 schreef Amoeba het volgende:

[..]

'
Ja precies. Ik vind uitspraken doen waarvan ik eigenlijk zeker weet dat ze niet per se waar zijn ook wel een dooddoener. Als je dan nog niet weet dat het bewijs eigenlijk niet waar is (ik was niet op de hoogte van de uitzondering van een degenerate distribution), dan blijf je rondjes lopen. Best vervelend om zo je tijd te moeten verspillen en dat je dan zo'n afgezaagd mailtje krijgt dat je 'picky' bent.

Ik zou gewoon even terugmailen

Ik heb de vergelijking
x/2 = (3/x)+p

Waarvan ze zeggen dat het antwoord moet zijn;
x1= p + wortel(p²+6)
x2= p - wortel(p²+6)

Als ik alle termen van x naar links haal hou ik over na vereenvoudigen;
x= -0,4P

quote:

Op dinsdag 29 september 2015 19:36 schreef nickname89 het volgende:
Ik heb de vergelijking
x/2 = (3/x)+p

Waarvan ze zeggen dat het antwoord moet zijn;
x1= p + wortel(p²+6)
x2= p - wortel(p²+6)

Als ik alle termen van x naar links haal hou ik over na vereenvoudigen;
x= -0,4P

Komt volgens mij gewoon neer op de abc-formule toepassen

quote:

Op dinsdag 29 september 2015 19:36 schreef nickname89 het volgende:
Ik heb de vergelijking
x/2 = (3/x)+p

Waarvan ze zeggen dat het antwoord moet zijn;
x1= p + wortel(p²+6)
x2= p - wortel(p²+6)

Als ik alle termen van x naar links haal hou ik over na vereenvoudigen;
x= -0,4P

Nee ...

Nu doe je net of je vergelijking luidt x/2 = 3x + p, maar dat staat er niet. Je moet dus om te beginnen beter uit je doppen kijken. We hebben



Nu zie je dat we in de breuk in het rechterlid de onbekende x in de noemer hebben staan. Het is zaak om eerst te zorgen dat je geen breuk meer hebt waar de onbekende in de noemer voorkomt. Hoe zou je dat hier aan kunnen pakken?

quote:

Op dinsdag 29 september 2015 21:20 schreef Riparius het volgende:

[..]

Nee ...

Nu doe je net of je vergelijking luidt x/2 = 3x + p, maar dat staat er niet. Je moet dus om te beginnen beter uit je doppen kijken. We hebben



Nu zie je dat we in de breuk in het rechterlid de onbekende x in de noemer hebben staan. Het is zaak om eerst te zorgen dat je geen breuk meer hebt waar de onbekende in de noemer voorkomt. Hoe zou je dat hier aan kunnen pakken?

Link en rechts vermenigvuldig met x. Dan krijg ik.
X^2/2=3+P
Dan vermenigvuldig met 2.
X^2=6+p^2

quote:

Op woensdag 30 september 2015 01:09 schreef nickname89 het volgende:

[..]

Link en rechts vermenigvuldigen met x. Dan krijg ik

X^2/2=3+P

Nee, dit is al fout. Vermenigvuldiging is immers distributief ten opzichte van optelling, dus als je beide leden met x vermenigvuldigt dan krijg je



Nu kunnen we de breuk in het linkerlid ook nog verdrijven door beide leden met 2 te vermenigvuldigen en dan krijgen we



Nu jij weer.

quote:

Op woensdag 30 september 2015 01:16 schreef Riparius het volgende:

[..]

Nee, dit is al fout. Vermenigvuldiging is immers distributief ten opzichte van optelling, dus als je beide leden met x vermenigvuldigt dan krijg je



Nu kunnen we de breuk in het linkerlid ook nog verdrijven door beide leden met 2 te vermenigvuldigen en dan krijgen we



Nu jij weer.

Omzetten naar een ax^2+bx+c.
X^2-2px-6=0

Abc formule
A=1
B=-2p
C=-6

Edit; zal de abc formule invullen als ik thuis ben zodat ik hem hier overzichtelijk kan weergeven