SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan ťťn of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan ťťn of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d


Weet het verder ook niet helaasquote:Op woensdag 3 juni 2015 19:40 schreef Holograph het volgende:
Nog een vraagje over kansrekening.
Zijeen continue stochast. Zij U een uniform verdeelde stochast op
, onafhankelijk van T. Wat is de verdeling van
. Ik zie hem alleen totaal niet.
moet nog wel lukken, maar hoe ik die laatste moet doen is mij niet duidelijk. Zou iemand mij een hint kunnen geven?
Regel van Bayesquote:Op donderdag 4 juni 2015 21:43 schreef Trias19 het volgende:
Dag iedereen,
Kan er iemand mij aub helpen met deze oefening? Het gaat over de voorwaardelijke kans en het lukt mij maar niet om dit op te lossen. Kan ik het ook oplossen met een boomdiagram?
Een psychotherapeut behandelt mensen met neurotische stoornissen meestal
(80%) met gesprekstherapie, terwijl voor psychotische stoornissen vaker een
combinatie van gedragstherapie en medicatie (70%) wordt toegepast. Indien
voor een bepaalde stoornis niet wordt gekozen voor de ene therapie, dan wordt
de andere toegepast. Stel dat 60% van de cliŽnten van deze psychotherapeut
worden behandeld voor een neurotische stoornis en 40% voor een psychotische
stoornis.
a) Als je nu weet dat de therapeut gesprekstherapie geeft aan een bepaalde cliŽnt,
hoe groot is dan de kans dat die lijdt aan een psychotische stoornis?
b) Stel dat je van 3 cliŽnten weet dat die gesprekstherapie krijgen, hoe groot is dan
de kans dat ze alle drie aan een psychose lijden?
Hier heb ik de gegevens opgesomt:
NS gespreksth =80%
PS gedragst & Med = 70%
NS = 60%
PS = 40%
[ Bericht 1% gewijzigd door Anoonumos op 04-06-2015 23:52:00 ]


Wilt er aub iemand mij zeggen of ik het juist oplos?
GT=gesprekstherapie, PS= psychotische stoornissen, NS = neurotische stoornis
Oplossing voor de eerste vraag : P(PS\GT) = (0,8* 0,4) / (0.8*0.4) + (0.3*0.6) = 0,64
Stoornissen:
NS= 0.6%
-GT =0.8%
-Niet GT = 0.2%
PS= 0.4%
-Gedrags & Med = 0.7%
- Niet Gedrags & Med = 0.3%
Hoe kan ik bij de vraag 2 die 3 cliŽnten selecteren? Hoe moet ik het opschrijven? P(..)
GT=gesprekstherapie, PS= psychotische stoornissen, NS = neurotische stoornis
Oplossing voor de eerste vraag : P(PS\GT) = (0,8* 0,4) / (0.8*0.4) + (0.3*0.6) = 0,64
Stoornissen:
NS= 0.6%
-GT =0.8%
-Niet GT = 0.2%
PS= 0.4%
-Gedrags & Med = 0.7%
- Niet Gedrags & Med = 0.3%
Hoe kan ik bij de vraag 2 die 3 cliŽnten selecteren? Hoe moet ik het opschrijven? P(..)


Waar je 0.8 het moet 0.3 staan (2 keer) en waar je 0.3 hebt moet 0.8 staanquote:Op vrijdag 5 juni 2015 22:41 schreef Trias19 het volgende:
Wilt er aub iemand mij zeggen of ik het juist oplos?
GT=gesprekstherapie, PS= psychotische stoornissen, NS = neurotische stoornis
Oplossing voor de eerste vraag : P(PS\GT) = (0,8* 0,4) / (0.8*0.4) + (0.3*0.6) = 0,64
P (PS | GT) = P (GT | PS) P (PS) / (P (GT | PS) P (PS) + P (GT | NS) P (NS)) = 0.3 * 0.4 / (0.3 * 0.4 + 0.8 * 0.6) = 0.2
Antwoord op B is dan het product van 3 keer de kans van antwoord A dus 0.23 = 0.008


Nee, dit had je gemakkelijk zelf kunnen inzien door jouw vermeende primitieve functie te differentiŽren.quote:Op zaterdag 6 juni 2015 13:22 schreef rareziekte het volgende:
de primitieve van 2(1-x)^-(1/2) geeft -4(1-x)^(1/2) + c
is het niet 4?
Door juist te primitiveren. Tip: merk op dat er een coŽfficiŽnt -1 voor x staat en ga dan nadenken over de kettingregel der differentiaalrekening.quote:


Ok, had die -x over het hoofd gezien, dankquote:Op zaterdag 6 juni 2015 14:16 schreef jungiaan het volgende:
[..]
Nee, dit had je gemakkelijk zelf kunnen inzien door jouw vermeende primitieve functie te differentiŽren.
[..]
Door juist te primitiveren. Tip: merk op dat er een coŽfficiŽnt -1 voor x staat en ga dan nadenken over de kettingregel der differentiaalrekening.


Bedankt, nu snap ik wat ik fout deed...quote:Op vrijdag 5 juni 2015 22:58 schreef Anoonumos het volgende:
[..]
Waar je 0.8 het moet 0.3 staan (2 keer) en waar je 0.3 hebt moet 0.8 staan
P (PS | GT) = P (GT | PS) P (PS) / (P (GT | PS) P (PS) + P (GT | NS) P (NS)) = 0.3 * 0.4 / (0.3 * 0.4 + 0.8 * 0.6) = 0.2
Antwoord op B is dan het product van 3 keer de kans van antwoord A dus 0.23 = 0.008


Ik probeer te bewijzen f(x)=1/sqrt(1-x2) geeft F(x)=arcsin(x)
Substitutie van x=sin(x) in f(x)dx geeft
1/sqrt(1-sin^2(t))dsin(t) = cos(t)/sqrt(1-sin^2(t))dt
Het boek neemt de noemer als sqrt cos^2(t)
Hoezo is 1-sin^2(t)=cos^2(t) ? Met de verdubbelingsformules kom ik er niet uit
[ Bericht 0% gewijzigd door rareziekte op 09-06-2015 19:00:31 ]
Substitutie van x=sin(x) in f(x)dx geeft
1/sqrt(1-sin^2(t))dsin(t) = cos(t)/sqrt(1-sin^2(t))dt
Het boek neemt de noemer als sqrt cos^2(t)
Hoezo is 1-sin^2(t)=cos^2(t) ? Met de verdubbelingsformules kom ik er niet uit
[ Bericht 0% gewijzigd door rareziekte op 09-06-2015 19:00:31 ]


cos^2(t) + sin^2(t) = 1 (eenheidscirkel en Pythagoras)quote:Op dinsdag 9 juni 2015 17:04 schreef rareziekte het volgende:
Ik probeer te bewijzen f(x)=1/sqrt(1-x2) geeft F(x)=arcsin(x)
Substitutie van x=sin(x) in f(x)dx geeft
1/sqrt(1-sin^2(t))dsin(t) = cos(t)/sqrt(1-sin^2(t))dt
Het boek neemt de noemer als sqrt cos^2(t)
Hoezo is 1-sin^(t)=cos^2(t) ? Met de verdubbelingsformules kom ik er niet uit
Dus het volgt direct dat 1 - sin^2(t)=cos^2(t).
Aangenomen dat je dat bedoelt (de typo).


Ah, dank. Stom. Jup, dat bedoelde ikquote:Op dinsdag 9 juni 2015 17:20 schreef Arthos het volgende:
[..]
cos^2(t) + sin^2(t) = 1 (eenheidscirkel en Pythagoras)
Dus het volgt direct dat 1 - sin^2(t)=cos^2(t).
Aangenomen dat je dat bedoelt (de typo).
Bij het berekenen van de oplossingen van een functie f(x) kom ik uiteindelijk uit op
-2x=-(1/2)pi + k2pi v 6x=-(1/2)pi+k2pi
Vervolgens geeft het boek
x= (1/4)pi + kpi v x=-(1/12)pi+k(1/3)pi
Waarom is het niet (1/4)pi - kpi?


k ranged over alle gehele getallen. In die context, is -kpi hetzelfde als +kpi.quote:Op dinsdag 9 juni 2015 19:10 schreef rareziekte het volgende:
[..]
Ah, dank. Stom. Jup, dat bedoelde ik
Bij het berekenen van de oplossingen van een functie f(x) kom ik uiteindelijk uit op
-2x=-(1/2)pi + k2pi v 6x=-(1/2)pi+k2pi
Vervolgens geeft het boek
x= (1/4)pi + kpi v x=-(1/12)pi+k(1/3)pi
Waarom is het niet (1/4)pi - kpi?
Immers, als x= (1/4)pi + kpi voor k=n, dan x= (1/4)pi - kpi voor k=-n. Als n een geheel getal is, is -n ook een geheel getal.
EDIT: Wauw, ik wist niet dat je kon TeXen hier. Maakt het leven makkelijker. Dus:
[ Bericht 8% gewijzigd door Arthos op 09-06-2015 21:58:48 ]


Als je vervolgens de oplossingen van die functie op domein [0,3pi] wilt geven neem je dusquote:Op dinsdag 9 juni 2015 19:29 schreef Arthos het volgende:
[..]
k ranged over alle gehele getallen. In die context, is -kpi hetzelfde als +kpi.
Immers, als x= (1/4)pi + kpi voor k=n, dan x= (1/4)pi - kpi voor k=-n. Als n een geheel getal is, is -n ook een geheel getal.
EDIT: Wauw, ik wist niet dat je kon TeXen hier. Maakt het leven makkelijker. Dus:
x=1/4 pi v x= (1/4pi) - -2*pi= 2 (1/4)pi ? Dan snap ik dat -kpi hier gelijk is aan +kpi
Bedankt.


Ik heb het idee dat je het nog niet begrijpt. Om te beginnen heeft een functie geen oplossingen. Je bedoelt waarschijnlijk de nulpunten van een functie f: [0, 3π] → R oftewel de oplossingen van een vergelijking f(x) = 0 op het interval [0, 3π]. Maar dan zijn er meer dan twee nulpunten van je functie f resp. oplossingen van je vergelijking f(x) = 0 op het interval [0, 3π].quote:Op woensdag 10 juni 2015 10:37 schreef rareziekte het volgende:
[..]
Als je vervolgens de oplossingen van die functie op domein [0,3pi] wilt geven neem je dus
x=1/4 pi v x= (1/4pi) - -2*pi= 2 (1/4)pi ? Dan snap ik dat -kpi hier gelijk is aan +kpi
Bedankt.


Kan iemand me helpen met de volgende opgave? X,Y onafhankelijk en standaard normaal verdeeld (dus gemiddelde 0, standaarddeviatie 1). We zoeken de kansdichtheid van 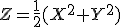 .
.
Als ik erop Google vind ik dingen over dat dit Chikwadraat verdeeld is ofzoiets, maar dat hebben we nog niet gehad. Hoe bepaal ik de kansdichtheid van Z? Alvast bedankt.
Verder loop ik vast op de marginale kansdichtheid fx van X bepalen, als X en Y gemeenschappelijk verdeeld zijn met:
![f_{X,Y}(x,y) := \frac{1}{2\pi \sqrt{1-\rho^2}} \cdot \exp\left[ - \frac{1}{2(1-\rho^2)}\left( x^2 + y^2 - 2\rho xy \right) \right]](https://forum.fok.nl/lib/mimetex.cgi?%20f_%7BX%2CY%7D%28x%2Cy%29%20%3A%3D%20%5Cfrac%7B1%7D%7B2%5Cpi%20%5Csqrt%7B1-%5Crho%5E2%7D%7D%20%5Ccdot%20%5Cexp%5Cleft%5B%20-%20%5Cfrac%7B1%7D%7B2%281-%5Crho%5E2%29%7D%5Cleft%28%20x%5E2%20%2B%20y%5E2%20-%202%5Crho%20xy%20%5Cright%29%20%5Cright%5D%20)
Dit komt neer op dit integreren over alle y. Ik krijg de volgende substitutie als hint:
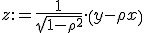
Als iemand me kan helpen met beide vragen, heel erg bedankt! Ik ben zo klaar met deze inleveropgave dat die integraal me niet lukt en bij die normale verdeling heb ik niet echt een idee hoe 't moet, vooral niet hoe ik moet beginnen.
[ Bericht 67% gewijzigd door Aardappeltaart op 10-06-2015 19:37:34 ]
Als ik erop Google vind ik dingen over dat dit Chikwadraat verdeeld is ofzoiets, maar dat hebben we nog niet gehad. Hoe bepaal ik de kansdichtheid van Z? Alvast bedankt.
Verder loop ik vast op de marginale kansdichtheid fx van X bepalen, als X en Y gemeenschappelijk verdeeld zijn met:
Dit komt neer op dit integreren over alle y. Ik krijg de volgende substitutie als hint:
Als iemand me kan helpen met beide vragen, heel erg bedankt! Ik ben zo klaar met deze inleveropgave dat die integraal me niet lukt en bij die normale verdeling heb ik niet echt een idee hoe 't moet, vooral niet hoe ik moet beginnen.
[ Bericht 67% gewijzigd door Aardappeltaart op 10-06-2015 19:37:34 ]


Sorry, ik bedoel een vergelijking in de vorm van cos(A)=cos(B), dat is geen functie idd. Er zijn dan twee oplossingen, maar ik wilde eigenlijk alleen zeker weten of bovenstaande oplossingen goed waren.quote:Op woensdag 10 juni 2015 17:17 schreef Riparius het volgende:
[..]
Ik heb het idee dat je het nog niet begrijpt. Om te beginnen heeft een functie geen oplossingen. Je bedoelt waarschijnlijk de nulpunten van een functie f: [0, 3π] → R oftewel de oplossingen van een vergelijking f(x) = 0 op het interval [0, 3π]. Maar dan zijn er meer dan twee nulpunten van je functie f resp. oplossingen van je vergelijking f(x) = 0 op het interval [0, 3π].


Als je wil weten of een bepaalde uitwerking of oplossing correct is, dan moet je wel het volledige vraagstuk posten, anders is je vraag onmogelijk te beantwoorden.quote:Op woensdag 10 juni 2015 20:33 schreef rareziekte het volgende:
[..]
Sorry, ik bedoel een vergelijking in de vorm van cos(A)=cos(B), dat is geen functie idd. Er zijn dan twee oplossingen, maar ik wilde eigenlijk alleen zeker weten of bovenstaande oplossingen goed waren.
Het is ook niet juist dat een vergelijking van de gedaante cos(A) = cos(B), waarin A en of B dan uitdrukkingen zijn in een onbekende, steeds twee oplossingen zou hebben. In het algemeen geldt wel het volgende:
Twee cosinussen zijn gelijk als de (rotatie)hoeken ůf gelijk zijn ůf tegengesteld, afgezien van een geheel veelvoud van 2π, dus
cos α = cos β ⇔ α = β + k∑2π ∨ α = −β + k∑2π, k ∈ Z
En ook geldt:
Twee sinussen zijn gelijk als de (rotatie)hoeken ůf gelijk zijn ůf supplementair, afgezien van een geheel veelvoud van 2π, dus
sin α = sin β ⇔ α = β + k∑2π ∨ α = π − β + k∑2π, k ∈ Z


Overigens is de tweede vraag ondertussen gelukt. Die met die som van kwadraten van normale verdeling helaas niet. Kan iemand helpen? Heel erg bedankt!!


Als je geen chi-squared verdeling hebt gehad wordt het lastig ben ik bangquote:Op donderdag 11 juni 2015 17:00 schreef Aardappeltaart het volgende:
Overigens is de tweede vraag ondertussen gelukt. Die met die som van kwadraten van normale verdeling helaas niet. Kan iemand helpen? Heel erg bedankt!!
Ze zullen niet verwachten dat je het zelf kan afleiden


Klopt dit qua conventies?:
• Als a = onsplitsbaar/atomair/geen verzameling (bijv a = integer 5), dan schrijf je a ∊ b
• Als a = (deel)verzameling (bijv. a = {2,4,9}), dan schrijf je a ⊆ b
• Als a = onsplitsbaar/atomair/geen verzameling (bijv a = integer 5), dan schrijf je a ∊ b
• Als a = (deel)verzameling (bijv. a = {2,4,9}), dan schrijf je a ⊆ b


Het verschil is idd of je het over een element hebt of over een deelverzameling.quote:Op donderdag 11 juni 2015 18:27 schreef topdeck het volgende:
Klopt dit qua conventies?:
• Als a = onsplitsbaar/atomair/geen verzameling (bijv a = integer 5), dan schrijf je a ∊ b
• Als a = (deel)verzameling (bijv. a = {2,4,9}), dan schrijf je a ⊆ b
Als
schrijven we:
en


Om te beginnen: ik ben tegen het gebruik van de notaties sin−1 en cos−1 voor arcsin resp. arccos, dus zal ik deze laatste notaties gebruiken. Als je wil weten waarom, dan moet je dit maar eens lezen.quote:Op donderdag 11 juni 2015 13:38 schreef GeorgeArArMartin het volgende:
[ afbeelding ]
Hoe kun je een dergelijke omschrijving uitvoeren?
Laten we zeggen dat
Dit impliceert dat
waarbij
Laten we tevens zeggen dat
Dit impliceert dat
waarbij
Goed, nu hebben we dus
waarbij uit (3) 0 ≤ α ≤ ½π en tevens (6) 0 ≤ β ≤ ½π volgt dat
Aangezien het domein van de arccos functie het interval [−1, 1] is en het bereik het interval [0, π] en deze functie strict monotoon dalend is, betekent dit dat er een unieke x ∈ [−1, 1] is zodanig dat
mits α ≥ β zodat α − β ≥ 0. Dan is ook
Om nu cos(α − β) en daarmee x te bepalen, maken we gebruik van de identiteit
Welnu, (2) sin α = 4/5 en (5) cos β = 12/13 kennen we al, dus nu moeten we alleen cos α en sin β nog bepalen. Dit is eenvoudig met behulp van de identiteit
Aangezien (3) 0 ≤ α ≤ ½π en tevens (6) 0 ≤ β ≤ ½π weten we dat cos α en sin β beiden niet negatief moeten zijn, en met behulp van (12) vinden we dan
en
Merk nu op dat sin α > sin β zodat inderdaad α > β waarmee α − β op het interval [0, ½π] ligt en daarmee binnen het bereik van de arccos functie.
Invullen van (2), (5), (13) en (14) in (11) geeft nu
en dus hebben we
zodat uit (7) en (16) inderdaad volgt dat
QED
Toegift: in de waarden cos α = 3/5, sin α = 4/5 en cos β = 12/13, sin β = 5/13 herkennen we de PythagoreÔsche tripletten (3, 4, 5) en (5, 12, 13). Nu is het zo dat het product van twee sommen van twee kwadraten van twee positieve gehele getallen steeds weer is te schrijven als een som van twee kwadraten van twee positieve gehele getallen, en wel op twee verschillende manieren, want we hebben
Vullen we nu in (18) en (19) a = 3, b = 4, c = 5, d = 12 in, dan krijgen we uit de PythagoreÔsche tripletten (3, 4, 5) en (5, 12, 13) twee nieuwe PythagoreÔsche tripletten (33, 56, 65) en (16, 63, 65), en nu herken je in het eerste van deze nieuwe tripletten de teller 56 en de noemer 65 van het quotiŽnt 56/65 in (17). De verklaring is dat de beide scherpe hoeken van een rechthoekige driehoek waarvan de zijden zich verhouden als (33, 56, 65) elk gelijk zijn aan een som resp. een verschil van twee scherpe hoeken van de rechthoekige driehoeken waarvan de zijden zich verhouden als (3, 4, 5) en (5, 12, 13), en datzelfde geldt voor een rechthoekige driehoek waarvan de zijden zich verhouden als (16, 63, 65).
Merk nog op dat we bij bovenstaande herleiding wegens (8) −½π ≤ α − β ≤ ½π ook hadden kunnen kiezen voor een herleiding tot een arcus sinus zonder daarbij te hoeven nagaan of werd voldaan aan α − β ≥ 0 aangezien de arcsin functie het interval [−½π, ½π] als bereik heeft. Daarvoor maken we gebruik van de identiteit voor sin(α − β) en dan vinden we sin(α − β) = 33/65 en dus
Hier zie je in de teller van het quotiŽnt 33/65 het getal 33 uit het PythagoreÔsche triplet (33, 56, 65) tevoorschijn komen, en dat is ook begrijpelijk, want uit (12) cos2φ + sin2φ = 1 volgt voor 0 ≤ φ ≤ ½π en als we cos φ = x stellen dat sin φ = √(1 − x2) en daarmee arccos(x) = arcsin(√(1 − x2)) voor 0 ≤ x ≤ 1. Zodoende is dus arccos(56/65) = arcsin(33/65) aangezien (56/65)2 + (33/65)2 = 1.
[ Bericht 0% gewijzigd door Riparius op 12-06-2015 05:18:06 ]


Wat is een handig geheugensteuntje om te onthouden:
sin(0π) = 0
sin(⅙π) = ½√1 = ½
sin(¼π) = ½√2
sin(⅓π) = ½√3
En nog een vraag: hoe kan je gemakkelijk inzien dat x = k*2π, x = ⅔π + k*2π, en x = -⅔π + k*2π herleid kunnen worden tot x = k*⅔π?
[ Bericht 0% gewijzigd door netchip op 11-06-2015 22:36:15 (typo) ]
sin(0π) = 0
sin(⅙π) = ½√1 = ½
sin(¼π) = ½√2
sin(⅓π) = ½√3
En nog een vraag: hoe kan je gemakkelijk inzien dat x = k*2π, x = ⅔π + k*2π, en x = -⅔π + k*2π herleid kunnen worden tot x = k*⅔π?
[ Bericht 0% gewijzigd door netchip op 11-06-2015 22:36:15 (typo) ]


Het is eenvoudiger om dit te onthouden als je de hoeken in graden uitdrukt, namelijk 0, 30, 45, 60 en 90 graden. Uiteraard moet je dan ook nog weten dat een gestrekte hoek, oftewel 180 graden, overeenkomt met π radialen. Een eenvoudig ezelsbruggetje: de sinus van de genoemde hoeken is nu achtereenvolgensquote:Op donderdag 11 juni 2015 22:07 schreef netchip het volgende:
Wat is een handig geheigensteuntje om te onthouden:
sin(0π) = 0
sin(⅙π) = ½√1 = ½
sin(¼π) = ½√2
sin(⅓π) = ½√3
½√0, ½√1, ½√2, ½√3, ½√4
en dus
0, ½, ½√2, ½√3, 1
en de cosinus van de genoemde hoeken krijg je achtereenvolgens door hetzelfde rijtje van rechts naar links op te schrijven.
Schets even een eenheidscirkel in een cartesisch assenstelsel en geef op de eenheidscirkel het punt aan dat je krijgt door het startpunt met coŲrdinaten (1; 0) om de oorsprong te roteren over een hoek van +⅔π rad (positieve zin, dus tegen de klok in) en geef op de eenheidscirkel tevens het punt aan dat je krijgt door het startpunt met coŲrdinaten (1; 0) om de oorsprong te roteren over een hoek van -⅔π rad (negatieve zin, dus met de klok mee).quote:En nog een vraag: hoe kan je gemakkelijk inzien dat x = k*2π, x = ⅔π + k*2π, en x = -⅔π + k*2π herleid kunnen worden tot x = k*⅔π?

