SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Dan zou ik als leek zeggen dat je ze gewoon op moet tellen.quote:Op maandag 24 november 2014 15:16 schreef Super-B het volgende:
[..]
Marginale opbrengsten functie (Marginal Revenues).
Opinion is the medium between knowledge and ignorance (Plato)
Dat dacht ik dus ook, maar in het boek is het snijpunt met de y-as op punt 20 en niet op punt 30.. (zoals je zou denken, na het optellen).quote:
[..]
Dan zou ik als leek zeggen dat je ze gewoon op moet tellen.
Het snijpunt van wat? De twee MR-formules hebben twee verschillende variabelen. Of zijn die toevallig op de een of andere manier afhankelijk?quote:
[..]
Dat dacht ik dus ook, maar in het boek is het snijpunt met de y-as op punt 20 en niet op punt 30.. (zoals je zou denken, na het optellen).
Opinion is the medium between knowledge and ignorance (Plato)
Is het nietquote:
[..]
Het snijpunt van wat? De twee MR-formules hebben twee verschillende variabelen. Of zijn die toevallig op de een of andere manier afhankelijk?
Q totaal = Q1 + Q2
Dus.. alles oplossen voor Q, optellen en vervolgens oplossen voor MR ?
Had de foute functie gepost... Hierbij nogmaals de goede:quote:
[..]
Het snijpunt van wat? De twee MR-formules hebben twee verschillende variabelen. Of zijn die toevallig op de een of andere manier afhankelijk?
MR1 = 100 - 2Q en MR2 = 60
Kan iemand mij aanwijzen waar ik de fout in ga:
[tex]
(x-3)^2 + x = 0
(x-3) = i*sqrt(x) v. x-3 = -i*sqrt(x)
sqrt(x) = 3 + i v. sqrt(x) = 3-i
x= (3 + i)^2 v. x = (3 - i)^2
x = 9 + 3i + -1 v x = 9 -3i + - 1
x = 8 + 3i v. x = 8 - 3i
[/tex]
[tex]
(x-3)^2 + x = 0
(x-3) = i*sqrt(x) v. x-3 = -i*sqrt(x)
sqrt(x) = 3 + i v. sqrt(x) = 3-i
x= (3 + i)^2 v. x = (3 - i)^2
x = 9 + 3i + -1 v x = 9 -3i + - 1
x = 8 + 3i v. x = 8 - 3i
[/tex]
Waarom schrijf je het kwadraat niet uit? Dan kun je de abc-formule gebruiken. Wat je nu doet is heel omslachtig en fout.quote:
Kan iemand mij aanwijzen waar ik de fout in ga:
[tex]
(x-3)^2 + x = 0
(x-3) = i*sqrt(x) v. x-3 = -i*sqrt(x)
sqrt(x) = 3 + i v. sqrt(x) = 3-i
x= (3 + i)^2 v. x = (3 - i)^2
x = 9 + 3i + -1 v x = 9 -3i + - 1
x = 8 + 3i v. x = 8 - 3i
[/tex]
Als je wil weten waar je de fout ingaat: van de tweede naar de derde regel klopt niet, je deelt beide kanten door sqrt(x), maar je vergeet 3 ook hierdoor te delen.
Oh jaquote:
[..]
Waarom schrijf je het kwadraat niet uit? Dan kun je de abc-formule gebruiken. Wat je nu doet is heel omslachtig en fout.
Als je wil weten waar je de fout ingaat: van de tweede naar de derde regel klopt niet, je deelt beide kanten door sqrt(x), maar je vergeet 3 ook hierdoor te delen.
. Dankje!
Als ik een rechte lijn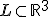 
en twee punten 
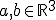heb, en ik ga deze twee punten loodrecht projecteren op de lijn L (gemakshalve noem ik de projecties a' en b' resp.).
Intuïtief zou ik dan zeggen dat:
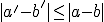
Klopt dit inderdaad? Zo ja, hoe zo ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Intuïtief zou ik dan zeggen dat:
Klopt dit inderdaad? Zo ja, hoe zo ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Dit moet niet zo moeilijk zijn.quote:
Als ik een rechte lijn
Intuïtief zou ik dan zeggen dat:
Klopt dit inderdaad? Zo ja, hoe zo ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Schrijf a' en b' als a en b en c, gebruik de driehoeksongelijkheid en volgens mij ben je er dan al.
[...] onzin
[ Bericht 20% gewijzigd door t4rt4rus op 25-11-2014 20:02:39 ]
Ik begrijp niet wat je hier doet. Er hoeft helemaal geen punt X op lijn ℓ te liggen waarvan de afstand tot de oorsprong gelijk is aan 1 en ook hoeven de loodrechte projecties A' en B' van A en B op ℓ helemaal niet collineair te zijn met de oorsprong.quote:
Ik dacht je neemt de eenheidsvector c op de lijn L, dan is de projectie van a op L, a', gegeven door a' = (a.c)c.quote:
[..]
Ik begrijp niet wat je hier doet. Er hoeft helemaal geen punt X op lijn ℓ te liggen waarvan de afstand tot de oorsprong gelijk is aan 1 en ook hoeven de loodrechte projecties A' en B' van A en B op ℓ helemaal niet collineair te zijn met de oorsprong.
Is dit dan wat beter?
Waarin
Stel de lijn L gaat door de oorsprong.
Neem een vector c parallel aan lijn L.
Dan is de projectie van a op L geven door
En de projectie van b door
Waaruit volgt dat
[ Bericht 7% gewijzigd door t4rt4rus op 25-11-2014 22:03:46 ]
Bedankt voor je reactie, maar volgens mij gaat dit niet werken...quote:
[..]
Dit moet niet zo moeilijk zijn.
Schrijf a' en b' als a en b en c, gebruik de driehoeksongelijkheid en volgens mij ben je er dan al.
Je definieert nu c als een verzameling, hoe is dan het inproduct van a met c gedefinieerd?
Tevens, de verzameling c kan ook leeg zijn, je kunt namelijk jouw c opvatten als de doorsnede van de lijn L met de bol met straal 1. Die doorsnede kan leeg zijn.
Edit: Sorry, ik zie nu dat Riparius dit al had opgemerkt en je hier al op hebt gereageerd, even lezen.
Nogmaals edit:
Je beschouwt dus de eenheidsvector c die de richting van de lijn L bepaalt.
Kom je dan niet in de problemen zodra L niet door de oorsprong gaat?
Derde update:
Nogmaals bedankt voor je herziene uitwerking, echter ga je er mijns inziens nu (onterecht) vanuit dat
[ Bericht 5% gewijzigd door Hahatsjoe op 25-11-2014 20:09:09 ]
quote:
[..]
Bedankt voor je reactie, maar volgens mij gaat dit niet werken...
Je definieert nu c als een verzameling, hoe is dan het inproduct van a met c gedefinieerd?
Tevens, de verzameling c kan ook leeg zijn, je kunt namelijk jouw c opvatten als de doorsnede van de lijn L met de bol met straal 1. Die doorsnede kan leeg zijn.
Edit: Sorry, ik zie nu dat Riparius dit al had opgemerkt en je hier al op hebt gereageerd, even lezen.
Nogmaals edit:
Je beschouwt dus de eenheidsvector c die de richting van de lijn L bepaalt.
Kom je dan niet in de problemen zodra L niet door de oorsprong gaat?
Derde update:
Nogmaals bedankt voor je herziene uitwerking, echter ga je er mijns inziens nu (onterecht) vanuit dat. Waarom mag je dit zeggen?
Voor een scalar a geldt toch |x c| = |x| |c| ?
[ Bericht 4% gewijzigd door t4rt4rus op 25-11-2014 21:17:07 ]
Ja.quote:
[..]
Voor een scalar a geldt toch |a c| = |a| |c| ?
Ik snap alleen niet hoe je nu precies die c introduceert. Volgens mij bedoel je dat je de lijn als het ware parametriseerd.
Immers, elk punt op de lijn L kun je schrijven als
waarbij r de richtingsvector is en s de steunvector (en t is de parameter).
Definieer je nu
Ik ben gewoon (namen van) lijnen met kleine letters aan te geven en (namen van) punten met hoofdletters, dus dat zal ik hier ook doen. We hebben in R3 een rechte ℓ en tevens twee punten A en B waarvan we veronderstellen dat deze verschillend zijn. Laten verder A' en B' de loodrechte projecties zijn van resp. A en B op ℓ. Gevraagd wordt nu te bewijzen dat d(A', B') ≤ d(A, B).quote:
Als ik een rechte lijn
Intuïtief zou ik dan zeggen dat:
Klopt dit inderdaad? Zo ja, hoe zou ik dit kunnen bewijzen?
Moet ik de directe formule voor een projectie gebruiken, of is het simpelweg een kwestie van de driehoeksongelijkheid toepassen?
Ik zie het zo snel niet in, hulp zou gewaardeerd worden.
Als A' = B' dan is er niets meer te bewijzen, zodat we A' ≠ B' mogen veronderstellen. Laten we nu de vectoren OA, OB, OA', OB' aangeven met resp. a, b, a', b', dan is
ℓ: v = a' + λ(b' − a')
een vectorvoorstelling van de rechte ℓ. Liggen de punten A en B niet op ℓ, dan staan de lijnstukken AA' en BB' beide loodrecht op lijnstuk A'B', zodat
(1) (a' − a)·(b' − a') = 0
en
(2) (b' − b)·(b' − a') = 0
Merk op dat (1) en (2) eveneens gelden als de punten A en of B wel op ℓ liggen, aangezien a' − a resp. b' − b dan de nulvector is. Uit (1) en (2) volgt nu
(3) a'·(b' − a') = a·(b' − a')
en
(4) b'·(b' − a') = b·(b' − a')
en daarmee
(5) (b' − a')·(b' − a') = (b − a)·(b' − a')
zodat
(6) | b' − a' |2 = | b − a | · | b' − a' | · | cos ∠(b − a, b' − a') |
Maar nu is A' ≠ B' zodat | b' − a' | ≠ 0 en dus hebben we
(7) | b' − a' | = | b − a | · | cos ∠(b − a, b' − a') |
en daarmee
(8) | b' − a' | ≤ | b − a |
QED
[ Bericht 0% gewijzigd door Riparius op 27-11-2014 17:42:50 ]
Je bent zo te zien nog steeds in de war. Eerst was je a een vector, en nu is het weer een scalar. En het is onduidelijk wat je nu wil met die genormeerde richtingsvector van de rechte, die heb je helemaal niet nodig.quote:
[..]
Ja, zo ja.
Sorry was net even in de war.
Oh die laatste zin van mij had niet veel met de rest te maken.quote:
[..]
Je bent zo te zien nog steeds in de war. Eerst was je a een vector, en nu is het weer een scalar. En het is onduidelijk wat je nu wil met die genormeerde richtingsvector van de rechte, die heb je helemaal niet nodig.
In de rest is a gewoon een vector.
Maar het ging hier toch om een projectie van de vectoren a en b op de lijn L?
Nemen we een vector c parallel met de lijn L dan zijn de projecties gegeven door
x' = (x.ĉ)ĉ
Je kunt volgens mij die vraag makkelijk bewijzen in R^2 en dan veralgemeniseren naar R^3 en zo naar R^n.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Nee, en dit is kennelijk je misverstand. Het gaat om de loodrechte projecties A' en B' van twee punten A resp. B op een rechte ℓ en om te bewijzen dat dan d(A', B') ≤ d(A, B).quote:
[..]
Oh die laatste zin van mij had niet veel met de rest te maken.
In de rest is a gewoon een vector.
Maar het ging hier toch om een projectie van de vectoren a en b op de lijn L?
Nemen we een vector c parallel met de lijn L dan zijn de projecties gegeven door
x' = (x.ĉ)ĉ
En laat ik dat in feite al hebben gedaan.quote:
Je kunt volgens mij die vraag makkelijk bewijzen in R^2 en dan veralgemeniseren naar R^3 en zo naar R^n.
Is dat niet gewoon hetzelfde als de projectie van de vectoren a en b op een vector c als we de lijn L door de oorsprong laten gaan?quote:
[..]
Nee, en dit is kennelijk je misverstand. Het gaat om de loodrechte projecties A' en B' van twee punten A resp. B op een rechte ℓ en om te bewijzen dat dan d(A', B') ≤ d(A, B).
De problemen zijn dan equivalent aan elkaar.
Het punt is dat de gegeven rechte ℓ niet door de oorsprong hoeft te gaan. Je lijkt ook niet te begrijpen dat de vier punten A, B, A' en B' niet in één vlak hoeven te liggen. Heb je mijn uitwerking bestudeerd en begrijp je deze ook?quote:
[..]
Is dat niet gewoon hetzelfde als de projectie van de vectoren a en b op een vector c als we de lijn L door de oorsprong laten gaan?
De problemen zijn dan equivalent aan elkaar.
