[Bèta wiskunde] Huiswerk- en vragentopic.

woensdag 22 oktober 2014 @ 16:21:34 #151

Nelvalhil

quote:
Op woensdag 22 oktober 2014 16:19 schreef t4rt4rus het volgende:

[..]

Volgens mij maak je nog een foutje, want er is maar één oplossing.

Nee. Het klopt, volgens mij

1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers

woensdag 22 oktober 2014 @ 16:23:09 #152

Nelvalhil

Hoezo zou het niet kloppen? N = 1 v N= 1 9/16

1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers

woensdag 22 oktober 2014 @ 16:26:09 #153

t4rt4rus

Tartarus

quote:
Op woensdag 22 oktober 2014 16:21 schreef Janneke141 het volgende:

[..]

Goed punt, de wortel van (5-100/16) bestaat natuurlijk niet.

Is het daarom niet handiger gelijk na het kwadrateren het domein aan te geven voor die vergelijking?
Op de middelbare school moesten we de oplossing weer terug invullen in de vergelijking om te controleren of hij klopt.
Maar als je gewoon gelijk het domein aangeeft hoef je dat helemaal niet te doen.

quote:
Op woensdag 22 oktober 2014 16:23 schreef Nelvalhil het volgende:
Hoezo zou het niet kloppen? N = 1 v N= 1 9/16

Na het kwadraten krijg je twee vergelijkingen de ene voor het domein x =< 5/4 en de andere x > 5/4.
De oplossing van de vergelijking die zij opgelost heeft zit niet in dat domein (19/16 > 5/4). Daarnaast heeft de andere vergelijking geen enkele oplossing in het domein.
Er is dus maar één oplossing.

woensdag 22 oktober 2014 @ 16:29:25 #154

Riparius

quote:
Op woensdag 22 oktober 2014 16:21 schreef Janneke141 het volgende:

[..]

Goed punt, de wortel van (5-100/16) bestaat natuurlijk niet.

Nee, maar daar gaat het hier niet om. De beide oplossingen van de vierkantsvergelijking in N zijn positief, dus √N bestaat voor elk van beide waarden van N die je vindt. Alleen is een vierkantswortel niet negatief waardoor de oplossing N = 25/16 komt te vervallen, maar dat is wat anders.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 22 oktober 2014 @ 16:32:04 #155

Janneke141

Green, green grass of home

Ik heb mijzelf inderdaad wat slordig verwoord. Excuus.

Want

quote:
Is het daarom niet handiger gelijk na het kwadrateren het domein aan te geven voor die vergelijking?

Opinion is the medium between knowledge and ignorance (Plato)

woensdag 22 oktober 2014 @ 16:32:58 #156

Nelvalhil

quote:
Op woensdag 22 oktober 2014 16:29 schreef Riparius het volgende:

[..]

Nee, maar daar gaat het hier niet om. De beide oplossingen van de vierkantsvergelijking in N zijn positief, dus √N bestaat voor elk van beide waarden van N die je vindt. Alleen is een vierkantswortel niet negatief waardoor de oplossing N = 25/16 komt te vervallen, maar dat is wat anders.

Dit ja

1 op de 6 mensen heeft 5 anderen om zich heen
-Harry Jekkers

woensdag 22 oktober 2014 @ 19:33:58 #157

netchip

Differentiëren lukt me nu wel aardig, al heb ik met dit (post van Riparius over de notatie van Leibniz) nog wel moeite, maar ook daar begint het kwartje te vallen.

Ik ben nu dus aan het kijken naar het integreren van een functie. Als je hebt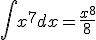 $\int x^7 dx = \frac{x^8}{8}$ , dan klinkt dat totaal logisch. De afgeleide van x⁸/8 zou gewoon x⁷ zijn. Maar nu ben ik dus aan het kijken naar integreren door substitutie, en dat ziet er voor mij een beetje als goochelen uit. Wanneer kan ik deze methode toepassen, en hoe werkt deze? Ik weet dat het het tegenovergestelde van de kettingregel is. Stel 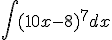$\int (10x-8)^7 dx$ , dan doe je de substitutie u = 10x-8. Oké, maar wat gebeurt er met de differentiaal dx? Zou iemand daar uitleg over kunnen geven?

woensdag 22 oktober 2014 @ 19:41:34 #158

Novermars

Als je u = 10x-8 hebt, dan heb je du/dx = 10 en "dus" du = 10dx. Dan heb je dus de integraal
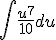
$\int \dfrac{u^7}{10} du$
Ik ben vergeten hoe je dit rigoureus opschrijft, maar dit is genoeg om te weten hoe je het kan toepassen.

woensdag 22 oktober 2014 @ 19:47:29 #159

netchip

quote:
Op woensdag 22 oktober 2014 19:41 schreef Novermars het volgende:
Als je u = 10x-8 hebt, dan heb je du/dx = 10 en "dus" du = 10dx. Dan heb je dus de integraal
$\int \dfrac{u^7}{10} du$
Ik ben vergeten hoe je dit rigoureus opschrijft, maar dit is genoeg om te weten hoe je het kan toepassen.

En dat wordt du, omdat je gaat integreren naar u? En... Je krijgt daar een deling door 10 omdat dx = du/10 = du * 1/10?

Als je dan $\int \dfrac{u^8}{80}du$ hebt, en je wilt dit weer substitueren met de waardes van u, krijg je dan $\int \dfrac{(10x-8)^8}{80}dx$ ? Waarom kan hier de du weer vervangen worden door dx zonder te delen door 10 (want dx = du/10)?

woensdag 22 oktober 2014 @ 19:55:52 #160

zerak

Exile Vilify

quote:
Op woensdag 22 oktober 2014 19:47 schreef netchip het volgende:

[..]

En dat wordt du, omdat je gaat integreren naar u? En... Je krijgt daar een deling door 10 omdat dx = du/10 = du * 1/10?

Als je dan $\int \dfrac{u^8}{80}du$ hebt, en je wilt dit weer substitueren met de waardes van u, krijg je dan $\int \dfrac{(10x-8)^8}{80}dx$ ? Waarom kan hier de du weer vervangen worden door dx zonder te delen door 10 (want dx = du/10)?

Nee, er volgt direct dat

$\int \frac{u^7}{10}du = \frac{u^8}{80} + C$

Nu kun je weer substitueren.

woensdag 22 oktober 2014 @ 19:56:42 #161

Novermars

quote:
Op woensdag 22 oktober 2014 19:47 schreef netchip het volgende:

[..]

En dat wordt du, omdat je gaat integreren naar u? En... Je krijgt daar een deling door 10 omdat dx = du/10 = du * 1/10?

Als je dan $\int \dfrac{u^8}{80}du$ hebt, en je wilt dit weer substitueren met de waardes van u, krijg je dan $\int \dfrac{(10x-8)^8}{80}dx$ ? Waarom kan hier de du weer vervangen worden door dx zonder te delen door 10 (want dx = du/10)?

Je hebt: $\int (10x-8)^7 dx \overset{\small u=10x-8}{=} \int \dfrac{u^7}{10}du = \dfrac{u^8}{80}+C \overset{\small u=10x-8}{=}\:\: \dfrac{(10x-8)^8}{80}+C$

woensdag 22 oktober 2014 @ 19:56:55 #162

netchip

quote:
Op woensdag 22 oktober 2014 19:55 schreef zerak het volgende:

[..]

Nee, er volgt direct dat

$\int \frac{u^7}{10}du = \frac{u^8}{80} + C$

Nu kun je weer substitueren.

Waarom mag je de differentiaal du hier vervangen door de integratieconstante?

woensdag 22 oktober 2014 @ 20:05:04 #163

zerak

Exile Vilify

quote:
Op woensdag 22 oktober 2014 19:56 schreef netchip het volgende:

[..]

Waarom mag je de differentiaal du hier vervangen door de integratieconstante?

Dat doe ik niet, ik evalueer hier gewoon de integraal. Overigens:

$\int x^7 dx \neq \frac{x^8}{8}$

Je vergeet hier de integratieconstante.

Ik raad je aan je eerst even wat beter te verdiepen in de zogenaamde 'u-substitution', want volgensmij is het nu nog abacadabra voor je. Hier alvast een link.

woensdag 22 oktober 2014 @ 21:11:31 #164

netchip

Even wat anders,

"De top van de grafiek van f(x) = x²+px+3 ligt op de lijn y = x+1."
Wat ik deed is x_top = -b/2a = -p/2, en dan zeggen f(-p/2) = x+1. Dit ging natuurlijk fout omdat ik dan twee variabelen heb, en in het uitwerkingenboek zeggen ze dat je de y_top moet invullen in y = x+1. Dit lijkt me sterk, want waarom vul je de y-coördinaat van een top van een parabool in in een formule voor een y-coödinaat?!

woensdag 22 oktober 2014 @ 21:52:10 #165

Riparius

quote:
Op woensdag 22 oktober 2014 19:33 schreef netchip het volgende:
Differentiëren lukt me nu wel aardig, al heb ik met dit (post van Riparius over de notatie van Leibniz) nog wel moeite, maar ook daar begint het kwartje te vallen.

Ik ben nu aan het kijken naar het integreren van een functie. Als je hebt $\int x^7 dx = \frac{x^8}{8}$ , dan klinkt dat totaal logisch. De afgeleide van x⁸/8 zou gewoon x⁷ zijn. Maar nu ben ik aan het kijken naar integreren door substitutie, en dat ziet er voor mij een beetje als goochelen uit. Wanneer kan ik deze methode toepassen, en hoe werkt deze? Ik weet dat het het tegenovergestelde van de kettingregel is. Stel $\int (10x-8)^7 dx$ , dan doe je de substitutie u = 10x-8. Oké, maar wat gebeurt er met de differentiaal dx? Zou iemand daar uitleg over kunnen geven?

Je geeft al aan dat de substitutieregel bij het integreren (c.q. primitiveren) de tegenhanger is van de kettingregel bij het differentiëren, en daarmee zou je antwoord kunnen geven op je eigen vraag. Als F een primitieve is van een reële functie f van een reële variabele x, dan hebben we

$\int f(x)\rm{d}x\,=\,F(x)\,+\,C$

waarbij C een willekeurige (reële) constante is. Een onbepaalde integraal van een functie is zo niets anders dan een notatie voor de verzameling van alle primitieven van de gegeven functie aangezien elk tweetal primitieven van een functie slechts een constante van elkaar verschilt. Deze notatie moet niet worden verward met de hoofdstelling van de integraalrekening die betrekking heeft op een bepaalde integraal en die zegt dat als f: [a,b] → R een continue functie is en F een primitieve van f, dat dan geldt

$\int_a^b f(x)\rm{d}x\,=\,F(b)\,-\,F(a)$

Kijk hier voor een eenvoudige uitleg van de hoofdstelling van de integraalrekening en de origine van deze notaties.

Substitueren we nu x = φ(u) waarbij φ een differentieerbare functie is, dan is de afgeleide van F(φ(u)) naar u volgens de kettingregel gelijk aan F'(φ(u))φ'(u) = f(φ(u))φ'(u), zodat omgekeerd F(φ(u)) een primitieve is van f(φ(u))φ'(u) en we dus hebben

$\int f(\varphi(u))\varphi'(u)\rm{d}u\,=\,F(\varphi(u))\,+\,C\,=\, F(x)\,+\,C$

en daarmee

$\int f(x)\rm{d}x\,=\,\int f(\varphi(u))\varphi'(u)\rm{d}u$

Is φ: [α,β] → [a,b] een differentieerbare functie met a = φ(α), b = φ(β) dan is F(b) − F(a) = F(φ(β)) − F(φ(α)) zodat we volgens de hoofdstelling van de integraalrekening ook hebben

$\int_a^b f(x)\rm{d}x\,=\,\int_{\alpha}^{\beta} f(\varphi(u))\varphi'(u)\rm{d}u$

De notatie en de symboliek van Leibniz maken het, evenals bij de kettingregel, weer gemakkelijk om de substitutieregel te onthouden en te gebruiken. Substitueren we

$x\,=\,\varphi(u)$

dan is

$\frac{\rm{d}x}{\rm{d}u}\,=\,\varphi'(u)$

en daarmee (symbolisch)

$\rm{d}x\,=\,\varphi'(u)\rm{d}u$

zodat je gemakkelijk onthoudt dat je dx door φ'(u)du moet vervangen als je x door φ(u) vervangt, zie ook hier.

In de praktijk gebruik je bovenstaande substitutieregel ook vaak van rechts naar links, en dan heb je als we de rollen van x en u verwisselen

$\int f(\varphi(x))\varphi'(x)\rm{d}x\,=\,\int f(u)\rm{d}u\,=\,F(u)\,+\,C\,=\,F(\varphi(x))\,+\,C$

Hier substitueren we

$u\,=\,\varphi(x)$

zodat

$\frac{\rm{d}u}{\rm{d}x}\,=\,\varphi'(x)$

en daarmee

$\rm{d}u\,=\,\varphi'(x)\rm{d}x$

zodat we weer gemakkelijk zien dat we φ'(x)dx moeten vervangen door du als we φ(x) vervangen door u. Is φ: [α,β] → [a,b] een differentieerbare functie met φ(α) = a, φ(β) = b, dan is F(φ(β)) − F(φ(α)) = F(b) − F(a) en hebben we dus volgens de hoofdstelling van de integraalrekening ook

$\int_{\alpha}^{\beta} f(\varphi(x))\varphi'(x)\rm{d}x\,=\,\int_a^b f(u)\rm{d}u$

Tot slot, aangezien we ook kunnen schrijven

$\frac{\rm{d}(\varphi(x))}{\rm{d}x}\,=\,\varphi'(x)$

en daarmee

$\rm{d}(\varphi(x))\,=\,\varphi'(x)\rm{d}x$

kunnen we ook schrijven

$\int f(\varphi(x))\varphi'(x)\rm{d}x\,=\,\int f(\varphi(x))\rm{d}(\varphi(x))\,=\,F(\varphi(x))\,+\,C$

hetgeen neerkomt op een impliciete substitutie. Immers, substitueren we u = φ(x) in

$\int f(\varphi(x))\rm{d}(\varphi(x))\,=\,F(\varphi(x))\,+\,C$

dan staat er niets anders dan

$\int f(u)\rm{d}u\,=\,F(u)\,+\,C$

Hebben we nu bijvoorbeeld

$\int (10x\,-\,8)^7\rm{d}x$

dan kunnen we bedenken dat

$\frac{\rm{d}(10x\,-\,8)}{\rm{d}x}\,=\,10$

en daarmee

$\rm{d}(10x\,-\,8)\,=\,10\cdot\rm{d}x$

oftewel

$\rm{d}x\,=\,\frac{1}{10}\cdot \rm{d}(10x\,-\,8)$

zodat

$\int (10x\,-\,8)^7\rm{d}x\,=\,\frac{1}{10}\int (10x\,-\,8)^7\rm{d}(10x\,-\,8)\,=\,\frac{1}{10}\cdot \frac{1}{8}\cdot(10x\,-\,8)^8\,+\,C\,=\,\frac{1}{80}(10x\,-\,8)^8\,+\,C$

[ Bericht 0% gewijzigd door Riparius op 27-10-2014 12:42:18 ]

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 22 oktober 2014 @ 22:10:53 #166

Riparius

quote:
Op woensdag 22 oktober 2014 21:11 schreef netchip het volgende:
Even wat anders,

"De top van de grafiek van f(x) = x²+px+3 ligt op de lijn y = x+1."
Wat ik deed is x_top = -b/2a = -p/2, en dan zeggen f(-p/2) = x+1. Dit ging natuurlijk fout omdat ik dan twee variabelen heb, en in het uitwerkingenboek zeggen ze dat je de y_top moet invullen in y = x+1. Dit lijkt me sterk, want waarom vul je de y-coördinaat van een top van een parabool in in een formule voor een y-coördinaat?!

Je begrijpt de opgave duidelijk niet. De top van de grafiek van f(x) = x² + px + 3 moet op de lijn met vergelijking y = x + 1 liggen, dus als de top van de grafiek van f de coördinaten (x_top; y_top) heeft, dan moeten deze coördinaten voldoen aan de betrekking

y_top = x_top + 1

Je bent er dus niet door alleen x_top uit te drukken in p, maar je moet ook y_top uitdrukken in p en dan beide uitdrukkingen invullen in deze betrekking, zodat je een vergelijking in p krijgt die je vervolgens op kunt lossen.

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 22 oktober 2014 @ 22:31:43 #167

netchip

quote:
Op woensdag 22 oktober 2014 22:10 schreef Riparius het volgende:

[..]

Je begrijpt de opgave duidelijk niet. De top van de grafiek van f(x) = x² + px + 3 moet op de lijn met vergelijking y = x + 1 liggen, dus als de top van de grafiek van f de coördinaten (x_top; y_top) heeft, dan moeten deze coördinaten voldoen aan de betrekking

y_top = x_top + 1

Je bent er dus niet door alleen x_top uit te drukken in p, maar je moet ook y_top uitdrukken in p en dan beide uitdrukkingen invullen in deze betrekking, zodat je een vergelijking in p krijgt die je vervolgens op kunt lossen.

Ik ging er van uit dat de waarde van y_top gelijk moest zijn aan x+1, omdat de lijn x+1 en de top elkaar moesten snijden. Ik snap nog steeds niet waarom ik de x- en y-coördinaten moet invullen, maar ik zal er nog even over nadenken.

woensdag 22 oktober 2014 @ 22:46:28 #168

Riparius

quote:
Op woensdag 22 oktober 2014 22:31 schreef netchip het volgende:

[..]

Ik ging er van uit dat de waarde van y_top gelijk moest zijn aan x+1, omdat de lijn x+1 en de top elkaar moesten snijden.

Dit is niet nauwkeurig genoeg, en dat is precies je probleem. Bedenk eens wat je hier bedoelt met x. En er is niet zoiets als een lijn x + 1. Je hebt een lijn met als vergelijking y = x + 1.

quote:
Ik snap nog steeds niet waarom ik de x- en y-coördinaten moet invullen, maar ik zal er nog even over nadenken.

De top van de parabool die de grafiek is van je kwadratische functie heeft de coördinaten (x_top; y_top) en gevraagd wordt nu p zo te bepalen dat deze top op de rechte met vergelijking y = x + 1 ligt, zodat geldt

y_top = x_top + 1

Nu had je al bedacht dat

x_top = −p/2

zodat je dus hebt

(1) y_top = −p/2 + 1

Maar je hebt ook

(2) y_top = f(x_top)

en uit (1) en (2) volgt

(3) f(x_top) = −p/2 + 1

oftewel

(4) f(−p/2) = −p/2 + 1

Wat denk je hiervan?

Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus

woensdag 22 oktober 2014 @ 22:56:13 #169

netchip

quote:
Op woensdag 22 oktober 2014 22:46 schreef Riparius het volgende:

[..]

Dit is niet nauwkeurig genoeg, en dat is precies je probleem. Bedenk eens wat je hier bedoelt met x. En er is niet zoiets als een lijn x + 1. Je hebt een lijn met als vergelijking y = x + 1.

[..]

De top van de parabool die de grafiek is van je kwadratische functie heeft de coördinaten (x_top; y_top) en gevraagd wordt nu p zo te bepalen dat deze top op de rechte met vergelijking y = x + 1 ligt, zodat geldt

y_top = x_top + 1

Nu had je al bedacht dat

x_top = −p/2

zodat je dus hebt

(1) y_top = −p/2 + 1

Maar je hebt ook

(2) y_top = f(x_top)

en uit (1) en (2) volgt

(3) f(x_top) = −p/2 + 1

oftewel

(4) f(−p/2) = −p/2 + 1

Wat denk je hiervan?

Ah, je hebt twee vergelijkingen voor lijnen, f(x) en y = x + 1. In beide moet je de x_top invullen, en dan gelijk stellen aan elkaar, omdat de waarde van f(x_top) gelijk moet zijn aan de waarde van x_top + 1. Dank je!

donderdag 23 oktober 2014 @ 08:41:39 #170

Borizzz

Thich Nhat Hanh

Leuke inzichtsvraag is dit trouwens. Ga ik onthouden

kloep kloep

donderdag 23 oktober 2014 @ 11:21:35 #171

Stickers

Wellicht is mijn vraag iets te simpel voor dit topic, maar goed

Ik heb moeite met het bewijzen van verzamelingen en het venndiagram die hierbij hoort.

Ik loop bijvoorbeeld vast als ik het venndiagram moet maken voor A ∩ ( B ∪ A ). Wat moet worden gearceerd, waar kruist A en B met elkaar

En het bewijzen van A ∩ ( B ∪ A ) = A

Voor mijzelf is bovenstaande logisch, het bewijzen hiervan blijkt echter lastiger dan gedacht

Poging tot bewijzen:
x ∈ A

x ∈ B ∪ A

Als x ∈ B ∪ A en x ∈ A dan is A ⊂ (B ∪ A)

Hier loop ik vast. Hoe werk ik dit verder uit?

donderdag 23 oktober 2014 @ 11:29:41 #172

t4rt4rus

Tartarus

quote:
Op donderdag 23 oktober 2014 11:21 schreef Stickers het volgende:
Wellicht is mijn vraag iets te simpel voor dit topic, maar goed

Ik heb moeite met het bewijzen van verzamelingen en het venndiagram die hierbij hoort.

Ik loop bijvoorbeeld vast als ik het venndiagram moet maken voor A ∩ ( B ∪ A ). Wat moet worden gearceerd, waar kruist A en B met elkaar

Teken twee cirkels die elkaar kruisen, de ene is A en de andere is B.
Wat is dan B ∪ A ?

donderdag 23 oktober 2014 @ 11:40:36 #173

Borizzz

Thich Nhat Hanh

quote:
Op donderdag 23 oktober 2014 11:29 schreef t4rt4rus het volgende:

[..]

Teken twee cirkels die elkaar kruisen, de ene is A en de andere is B.
Wat is dan B ∪ A ?

SPOILER
Om spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.

kloep kloep

donderdag 23 oktober 2014 @ 11:42:15 #174

Stickers

quote:
Op donderdag 23 oktober 2014 11:29 schreef t4rt4rus het volgende:

[..]

Teken twee cirkels die elkaar kruisen, de ene is A en de andere is B.
Wat is dan B ∪ A ?

Aangezien A wordt verenigd met B, is het resultaat een venndiagram die alle elementen bevat van zowel A als B. Vandaar dezelfde kleur

donderdag 23 oktober 2014 @ 11:50:18 #175

t4rt4rus

Tartarus

quote:
Op donderdag 23 oktober 2014 11:42 schreef Stickers het volgende:

[..]

[ afbeelding ]

Aangezien A wordt verenigd met B, is het resultaat een venndiagram die alle elementen bevat van zowel A als B. Vandaar dezelfde kleur

Oké, noemen we die set C, wat is dan A ∩ C?

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs