SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Wat heb je voor g(x) geprobeerd dan?quote:Op donderdag 9 oktober 2014 20:50 schreef RustCohle het volgende:
Ik kwam bij de afgeleide van g'(x) niet uit, laat staan g'(x) vinden met log. differentiëren. Bij die eerste deed ik het volgende:
[...]
"solven" is oplossen, dus los een vergelijking voor P op en neem de afgeleide.quote:Mijn derde vraag is het volgende:
Hoe kan ik van de volgende functie het 'solven' voor P en vervolgens dP/dQ vinden:
Q = ea P -b
Wat lukt hier niet?


Voor P oplossen wordt het :quote:Op donderdag 9 oktober 2014 21:24 schreef t4rt4rus het volgende:
[..]
Wat heb je voor g(x) geprobeerd dan?
[..]
"solven" is oplossen, dus los een vergelijking voor P op en neem de afgeleide.
Wat lukt hier niet?
Q / ea = P-b
Maar dat is dus niet goed..


Nee P-b is ook geen P...quote:Op donderdag 9 oktober 2014 21:36 schreef RustCohle het volgende:
[..]
Voor P oplossen wordt het :
Q / ea = P-b
Maar dat is dus niet goed..
Dus hoe krijg je dat weg?
En wat heb je voor die andere gedaan?


De clou van logaritmisch differentiëren is dat je eerst van beide leden de (natuurlijke) logaritme neemt en dan beide leden differentieert. Welnu, je hebtquote:Op donderdag 9 oktober 2014 20:50 schreef RustCohle het volgende:
Hallo.. Ik heb een drietal vragen:
Voor de volgende twee functies moet ik de logaritmes differentiëren toepassen om y'/y te vinden:
f(x) = ((x+1) / (x-1) ) 1/3
en
g(x) = √(x-2) (x²+1) (x4 + 6)
Ik kwam bij de afgeleide van g'(x) niet uit, laat staan g'(x) vinden met log. differentiëren. Bij die eerste deed ik het volgende:
y = ((x+1) / (x-1) ) 1/3
ln y = ln (x+1)1/3 - ln(x-1) 1/3
y' / y = 1/3 * 1/(x+1) - 1/3 * 1/(x-1)
en dus
zodat
Vermenigvuldig eerst beide leden met PbQ−1 en je hebtquote:Mijn derde vraag is het volgende:
Hoe kan ik van de volgende functie het 'solven' voor P en vervolgens dP/dQ vinden:
Q = ea P -b
en dus
en dit geeft
en dus
zodat


Goed opgemerkt. Er had moeten staan dat de functie f niet differentieerbaar is in het punt x = 2. Voor elke andere waarde van x uit het domein is deze functie f wel differentieerbaar. Maar je moet even nakijken welke definitie ze precies hanteren voor een differentieerbare functie tout court.quote:Op donderdag 9 oktober 2014 22:01 schreef Super-B het volgende:
[ afbeelding ]
Waarom staat er op het einde dat f(x) niet differentieerbaar is? Het is tóch juist wel differentieerbaar, alleen het is niet differentieerbaar op het punt x = 2.. (?)


De definitie is dat het overal differentieerbaar moet zijn...quote:Op donderdag 9 oktober 2014 22:01 schreef Super-B het volgende:
[ afbeelding ]
Waarom staat er op het einde dat f(x) niet differentieerbaar is? Het is tóch juist wel differentieerbaar, alleen het is niet differentieerbaar op het punt x = 2.. (?)
Dit kon je niet zelf bedenken?


quote:Op donderdag 9 oktober 2014 22:09 schreef t4rt4rus het volgende:
[..]
De definitie is dat het overal differentieerbaar moet zijn...
Dit kon je niet zelf bedenken?


Je moet hier gewoon goed naar het gegeven functievoorschrift kijken voor f(x) en de definitie voor continuïteit hanteren. Een reële functie f van een reële variabele gedefinieerd op een domein Df is continu indien f continu is voor elke a ∈ Df en een functie f is continu in een punt a ∈ Df dan en slechts dan als limx→a f(x) = f(a). En dat is hier het geval voor elke a ∈ R terwijl R het domein is van deze functie.quote:Op donderdag 9 oktober 2014 22:06 schreef Super-B het volgende:
Ten tweede:
[ afbeelding ]
Waarom is de functie continu voor alle x, terwijl (2x - 2)/ ln (x) alleen continu is als x > 0, Dus dan zou de hele functie toch continu moeten zijn als x > 0? Daarnaast waarom x > 0 en niet x > 1? Want als x = 1 dan is de noemer 0...


Dat trucje van logaritmisch differentiëren kende ik nog niet trouwens.quote:Op donderdag 9 oktober 2014 21:54 schreef Riparius het volgende:
[..]
De clou van logaritmisch differentiëren is dat je eerst van beide leden de (natuurlijke) logaritme neemt en dan beide leden differentieert. Welnu, je hebt
en dus
zodat
[..]
Vermenigvuldig eerst beide leden met PbQ−1 en je hebt
en dus
en dit geeft
en dus
zodat
Fervent tegenstander van het korps lasergamers.


Het is niet echt iets waarvoor deze draad is bedoeld, helaas misschien, maar het lijkt me aardig om het toch maar eens te doen.
Ik kwam een interessant vraagstuk tegen wat gemakkelijk te begrijpen is maar desalniettemin erg leerzaam is.
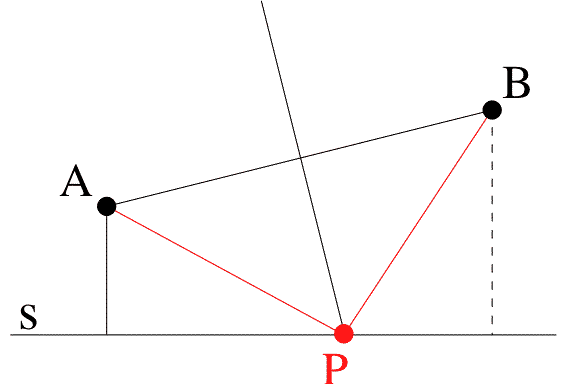
Heron's probleem. De vraag. Plaatsen A en B liggen langs een rivier, je moet via die rivier van A naar B. Wat is de kortste weg? Probeer het geometrisch op te lossen als je het zelf probeert, niet met rekenen.
[ Bericht 5% gewijzigd door Bram_van_Loon op 09-10-2014 23:57:42 ]
Ik kwam een interessant vraagstuk tegen wat gemakkelijk te begrijpen is maar desalniettemin erg leerzaam is.
Heron's probleem. De vraag. Plaatsen A en B liggen langs een rivier, je moet via die rivier van A naar B. Wat is de kortste weg? Probeer het geometrisch op te lossen als je het zelf probeert, niet met rekenen.
[ Bericht 5% gewijzigd door Bram_van_Loon op 09-10-2014 23:57:42 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL


Ik ben even in de war met iets.. als h richting 0 gaat vanaf de linkerkant.. dan wordt het toch geen 3, maar 0/0?quote:Op donderdag 9 oktober 2014 22:01 schreef Super-B het volgende:
[ afbeelding ]
Waarom staat er op het einde dat f(x) niet differentieerbaar is? Het is tóch juist wel differentieerbaar, alleen het is niet differentieerbaar op het punt x = 2.. (?)


Waarom vermenigvuldig je ook met Q-1?quote:Op donderdag 9 oktober 2014 21:54 schreef Riparius het volgende:
[..]
De clou van logaritmisch differentiëren is dat je eerst van beide leden de (natuurlijke) logaritme neemt en dan beide leden differentieert. Welnu, je hebt
en dus
zodat
[..]
Vermenigvuldig eerst beide leden met PbQ−1 en je hebt
en dus
en dit geeft
en dus
zodat


Als ik dat niet zou doen, dan zou in het linkerlid een factor Q blijven staan, en dat wil ik niet, want ik wil een gelijkheid krijgen waarbij in het linkerlid alleen P voorkomt. Uiteraard is vermenigvuldigen met Q−1 hetzelfde als delen door Q.quote:Op vrijdag 10 oktober 2014 00:43 schreef RustCohle het volgende:
[..]
Waarom vermenigvuldig je ook met Q-1?


Niemand kan die vraag met zekerheid beantwoorden als je niet de oorspronkelijke opgave laat zien, maar alleen een fragment van een uitwerking.quote:
Welke afgeleide van welke functie? En hoezo 'dus' ? Ik zie helemaal geen gevolgtrekking.quote:Ik had dat de afgeleide dus (-2y)-2 is
Nee, wat je hier beweert is met zekerheid fout. Leer nu eindelijk eens rekenregels voor machten (en ook voor breuken, wortels, logaritmen ...) alsmede haakjes consequent toe te passen. We hebbenquote:en de afgeleide daar weer van is dan:
(4y-3 )
voor a, b ∈ R+, p ∈ R, waarbij a en of b evenwel ook negatief mogen zijn als p geheel is, en dus hebben we
en de afgeleide hiervan naar y is
Maar wat je bedoelde maar niet opschreef was wellicht
en de afgeleide naar y hiervan is inderdaad
Hola! Nog meer onzin. Om te beginnen, wat bedoel je hier precies mee,quote:en dus: 1/4y³,
of
?
En dan nog: hoe kom je erbij dat 4y−3 opeens verandert in hetzij (1/4)·y3 hetzij 1/(4y3) louter en alleen door haakjes om 4y−3 te zetten? Het is natuurlijk conform bovenstaande rekenregel alsmede de rekenregel (ap)q = apq wel zo dat
maar het is niet in te zien waarom je hier meent het omgekeerde te moeten nemen van een afgeleide die je zojuist hebt berekend.
Ja, dat is voor jouw een vraag, en zeker gezien het scala aan goocheltrucs dat je hier ten beste geeft. Zoals gezegd is je vraag feitelijk niet te beantwoorden omdat je de oorspronkelijke opgave achterhoudt, maar ik doe een poging tot reconstructie. Als we hebbenquote:dus hoe komen ze op 1/y³ ?
dan is de inverse van deze functie
Goed, nu gaan we eens lekker differentiëren. De eerste afgeleide wordt
en hiervoor kunnen we uiteraard ook schrijven
Nu is het verder een kwestie van braaf de regel
toepassen. Voor de tweede afgeleide krijgen we zo
en de derde afgeleide wordt nu
Nog even een opmerking over de Leibniz notatie voor hogere afgeleiden. Zoals eerder uiteengezet kunnen we schrijven
waarbij we
dus als operator voor differentiatie naar x kunnen opvatten, zodat we voor de tweede afgeleide naar x zouden kunnen schrijven
Nu heeft Leibniz al bedacht dat je voor iets als
louter symbolisch
en daarmee ook
kunt schrijven en zo dus in het algemeen als operator voor de n-de afgeleide naar x
zodat we dus hebben
Overigens laat men de haakjes rond dx meestal weg, dus je zult ook vaak de notatie
of
tegenkomen voor wat in de notatie van Lagrange als
wordt geschreven, en waarbij we voor n < 4 gewoonlijk primes gebruiken, dus f'(x), f''(x) en f'''(x). Zie ook hier. Verwar de superscript n in de Leibniz notatie van de n-de afgeleide vooral niet met een exponent van een uitdrukking waarvan een afgeleide wordt genomen. Je hebt voor n ∈ N bijvoorbeeld
maar
waarvoor je ook
kunt schrijven, terwijl
en dus voor elke n > 1 ook
oftewel
[ Bericht 0% gewijzigd door Riparius op 12-10-2014 04:37:45 ]


Ik heb vandaag een tentamen en ik heb een klein vraagje:
Waarom is f(x) continu voor alle waarden van x? Het is toch juist continu voor alle waarden x > 0 ?
[ Bericht 43% gewijzigd door GeschiktX op 10-10-2014 09:52:49 ]
Waarom is f(x) continu voor alle waarden van x? Het is toch juist continu voor alle waarden x > 0 ?
[ Bericht 43% gewijzigd door GeschiktX op 10-10-2014 09:52:49 ]


quote:Op vrijdag 10 oktober 2014 09:46 schreef GeschiktX het volgende:
Ik heb vandaag een tentamen en ik heb een klein vraagje:
[ afbeelding ]
[ afbeelding ]
Waarom is f(x) continu voor alle waarden van x? Het is toch juist continu voor alle waarden x > 0 ?
f(x) is gedefinieerd als
Dan dus we weten dat f(x) in iedergeval continue voor alle
Dan hoef je dus alleen nog maar te kijken naar het punt x = 1, beiden hebben een limiet van 2 voor x = 1.
En dus geldt dat f(x) is continu.


Zelfde probleem staat hier ook al:quote:Op vrijdag 10 oktober 2014 09:46 schreef GeschiktX het volgende:
Ik heb vandaag een tentamen en ik heb een klein vraagje:
[ afbeelding ]
[ afbeelding ]
Waarom is f(x) continu voor alle waarden van x? Het is toch juist continu voor alle waarden x > 0 ?
SES / [Bèta wiskunde] Huiswerk- en vragentopic.
Het functievoorschrift is
f(x) = x6 - 2x3 + 3x, voor alle x≤1.
Dat polynoom is continu op heet R, dus zeker ook voor alle x≤1. Dus hoe je er precies bij komt dat de functie niet continu zou zijn voor x≤0 ontgaat me.
Opinion is the medium between knowledge and ignorance (Plato)


f is niet gedefinieerd in x=2 en kan dus per definitie niet continu zijn. Probeer de grafiek op het interval [1,2] maar eens te tekenen zonder je pen van het papier te halen. Dat lukt je niet.
En verder kan f(x) niet continu zijn, aangezien dat slechts een getal is. De functie f kan daarentegen wel continu zijn.
En als laatste, er zijn functies die wel continu zijn (op een deelverzameling van het domein) maar je niet kunt tekenen zonder je pen van het papier te halen. Thomae's functie bijvoorbeeld.
En verder kan f(x) niet continu zijn, aangezien dat slechts een getal is. De functie f kan daarentegen wel continu zijn.
En als laatste, er zijn functies die wel continu zijn (op een deelverzameling van het domein) maar je niet kunt tekenen zonder je pen van het papier te halen. Thomae's functie bijvoorbeeld.