SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni



Kettingregel, f(x) = g ( h(x) ), dan f'(x) = g' ( h(x) ) * h'(x)
Opinion is the medium between knowledge and ignorance (Plato)


Is er een andere manier?quote:Op maandag 23 juni 2014 21:12 schreef Novermars het volgende:
Moet het echt met de definitie? Zoja, dan heb ik medelijden met je...


Sla ik dan niet een aantal stappen over? Want ik heb nu het idee dat (sin(dx2+dx))/dx en (1-cos(dx2+dx)/dx naar iets neigen als het limiet dx 0 nadert... Of bedoel je dat ik de ''limiettermen'' als h(x) moet benoemen en dan de kettingregel moet toepassen? Dan behoud ik de limieten toch wel lijkt me?quote:Op maandag 23 juni 2014 21:12 schreef Janneke141 het volgende:
Kettingregel, f(x) = g ( h(x) ), dan f'(x) = g' ( h(x) ) * h'(x)


Zoals hierboven gezegd is: Kettingregel.quote:
Verder nog over je notatie: Zeggen dat
Wat is je niveau eigenlijk? Dat is ook altijd handig om te weten.


Hangt ervan af wat de opdracht is. Iedere 5-VWO'er gebruikt hier de kettingregel voor, maar als je in een theoretisch hoofdstuk over definities van differentieerbaarheid zit dan wordt er misschien wat anders van je verwacht.quote:Op maandag 23 juni 2014 21:16 schreef GeorgeArArMartin het volgende:
[..]
Sla ik dan niet een aantal stappen over? Want ik heb nu het idee dat (sin(dx2+dx))/dx en (1-cos(dx2+dx)/dx naar iets neigen als het limiet dx 0 nadert... Of bedoel je dat ik de ''limiettermen'' als h(x) moet benoemen en dan de kettingregel moet toepassen? Dan behoud ik de limieten toch wel lijkt me?
VWO lees ik, dus gewoon de kettingregel gebruiken. Zie mijn eerdere post, waarbij g(x) = sin x en h(x) = x2+x
Opinion is the medium between knowledge and ignorance (Plato)


Oh, bedankt!quote:Op maandag 23 juni 2014 21:17 schreef Novermars het volgende:
[..]
Zoals hierboven gezegd is: Kettingregel.
Verder nog over je notatie: Zeggen datis overbodig, dat gebeurt altijd.
Wat is je niveau eigenlijk? Dat is ook altijd handig om te weten.
Vwo, volgend jaar moet ik Wiskunde D voor het eerst volgen.


Sorry dat ik nogal traag overkom, het is dat ik dit nog nooit gehad heb... Afgelopen jaar heb ik alleen wiskunde B gehad en daar kwamen dit soort dingen zo goed als niet voor. Ik heb momenteel ook geen docent aan wie ik vragen kan stellen.
Dit is het bewijs dat ik op een oefenblad heb gekregen:
In het voorbeeld wordt de afgeleide van sin(x) gedefinieerd op dezelfde manier waarbij gonio. identiteiten gebruikt worden, ik denk dat ik het op dezelfde manier moet doen.quote:Op maandag 23 juni 2014 21:19 schreef Janneke141 het volgende:
[..]
Hangt ervan af wat de opdracht is. Iedere 5-VWO'er gebruikt hier de kettingregel voor, maar als je in een theoretisch hoofdstuk over definities van differentieerbaarheid zit dan wordt er misschien wat anders van je verwacht.
Dit is het bewijs dat ik op een oefenblad heb gekregen:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Is er ook een andere manier, waarmee het te bewijzen is? Of moet ik dan gebruik maken van het bewijs dat de afgeleide van sin(x), cos(x) is en dat de kettingregel klopt?quote:Op maandag 23 juni 2014 21:19 schreef Janneke141 het volgende:
[..]
Hangt ervan af wat de opdracht is. Iedere 5-VWO'er gebruikt hier de kettingregel voor, maar als je in een theoretisch hoofdstuk over definities van differentieerbaarheid zit dan wordt er misschien wat anders van je verwacht.
VWO lees ik, dus gewoon de kettingregel gebruiken. Zie mijn eerdere post, waarbij g(x) = sin x en h(x) = x2+x


Wordt er gevraagd om te bewijzen dat de afgeleide is wat ie is, of wordt er alleen om de afgeleide gevraagd? Want het bewijs in je afbeelding is het bewijs dat sin'(x)=cos(x) maar dat hoef je niet iedere keer dat je dat gebruikt, te geven natuurlijk.
Opinion is the medium between knowledge and ignorance (Plato)


Er is alleen gezegd dat ik moet aantonen dat f'(x) = (2x + 1 )cos(x2 + x) de afgeleide is van f(x)= sin(x2 + x)
Normaliter zou ik even bij de antwoorden kijken zodat ik weet wat hij voor antwoord verwacht, maar helaas is dit een door hemzelf samengesteld schrift zonder antwoorden.
Normaliter zou ik even bij de antwoorden kijken zodat ik weet wat hij voor antwoord verwacht, maar helaas is dit een door hemzelf samengesteld schrift zonder antwoorden.


Gezien het niveau (VWO) lijkt het me voldoende dat je de bekende rekenregels op de goede manier gebruikt en uitwerkt. Zie boven.quote:Op maandag 23 juni 2014 21:36 schreef GeorgeArArMartin het volgende:
Er is alleen gezegd dat ik moet aantonen dat f'(x) = (2x + 1 )cos(x2 + x) de afgeleide is van f(x)= sin(x2 + x)
Normaliter zou ik even bij de antwoorden kijken zodat ik weet wat hij voor antwoord verwacht, maar helaas is dit een door hemzelf samengesteld schrift zonder antwoorden.
Opinion is the medium between knowledge and ignorance (Plato)


Dus f(x)= g(u(x)) met g(u)= sin(u) en u= x2 + x
f'(x)= g'(u(x))u'(x)
Waardoor u'= 2x + 1
en g(u) = cos(u)
en dus f'(x) = cos(x2 + x)(2x+1) klopt/voldoet?
f'(x)= g'(u(x))u'(x)
Waardoor u'= 2x + 1
en g(u) = cos(u)
en dus f'(x) = cos(x2 + x)(2x+1) klopt/voldoet?


je moet niet dezelfde letter u tegelijk gebruiken als (1) een naam van een variable en (2) een naam van een functie, dat is conceptueel fout.quote:Op maandag 23 juni 2014 21:41 schreef GeorgeArArMartin het volgende:
Dus f(x)= g(u(x)) met g(u)= sin(u) en u= x2 + x
f'(x)= g'(u(x))u'(x)
Waardoor u'= 2x + 1
en g(u) = cos(u)
en dus f'(x) = cos(x2 + x)(2x+1) klopt/voldoet?
Als je toch wil werken met een 'tussenvariabele', dan is het handiger om gebruik te maken van de kettingregel in de notatie van Leibniz
dy/dx = dy/du · du/dx
Zie ook hier en hier.
Voor deze opgave heb je
u = x2 + x
en
y = sin u
zodat
dy/du = cos u = cos(x2 + x)
en
du/dx = 2x + 1
en dus
dy/dx = cos(x2 + x)·(2x + 1).
Je kunt het ook opschrijven in de notatie van Leibniz zonder gebruik te maken van een 'tussenvariabele', dan wordt het
d(sin(x2 + x))/dx = d(sin(x2 + x))/d(x2 + x) · d(x2 + x)/dx = cos(x2 + x)·(2x + 1).
Tenzij dit expliciet in de opgave wordt gevraagd, is het niet nodig om de afgeleide van een gegeven functie aan te tonen aan de hand van de definitie van de afgeleide.
Wil je dit toch, dan moet je het wel correct doen. Wat je hierboven doet lijkt nergens op. Om te beginnen verwar je een differentiaal dx met een (finiet) increment van je onafhankelijke variabele x, en zo'n increment wordt gewoonlijk aangegeven met Δx maar ook met de kleine letter h. En dan zit je ook nog te goochelen met je algebraïsche herleidingen (hint: leer je merkwaardige producten).
Het is de bedoeling dat je eerst een uitdrukking opschrijft voor f(x + h) zodat je vervolgens
Δy = f(x + h) − f(x)
kunt herleiden. Je krijgt dan voor jouw opgave een verschil van twee sinussen, en het is dan het handigst om niet gebruik te maken van het additietheorema voor sin(α + β) zoals dat wordt gedaan in het bewijs voor de afgeleide van de sinusfunctie dat je had gekregen, maar om gebruik te maken van de formule van Simpson voor het verschil van twee sinussen
sin θ − sin φ = 2·sin½(θ − φ)·cos½(θ + φ)
Dan deel je Δy = f(x + h) − f(x) door Δx = h om het differentiequotiënt Δy/Δx = (f(x + h) − f(x))/h te bepalen, waarvan je dan weer - na nog wat verdere herleiding - de limiet voor h → 0 kunt bepalen om f'(x) te vinden. Hiervoor zul je gebruik moeten maken de 'standaardlimiet'
limθ→0 sin θ / θ = 1
[ Bericht 18% gewijzigd door Riparius op 24-06-2014 18:30:20 ]


Volgens mij bedoelen ze met aantonen wat anders dan met bewijzen. Ook al een paar keer overgestruikeld.quote:Op maandag 23 juni 2014 21:36 schreef GeorgeArArMartin het volgende:
Er is alleen gezegd dat ik moet aantonen dat f'(x) = (2x + 1 )cos(x2 + x) de afgeleide is van f(x)= sin(x2 + x)
Normaliter zou ik even bij de antwoorden kijken zodat ik weet wat hij voor antwoord verwacht, maar helaas is dit een door hemzelf samengesteld schrift zonder antwoorden.


Lijkt me niet dat er een verschil is. Hooguit word je geacht het wat formeler op te schrijven als er naar een bewijs wordt gevraagd. Maar de vragensteller maakt niet duidelijk wat nu precies de bedoeling is, en wat hij wel en niet bekend mag veronderstellen, en dan is zijn vraag niet goed te beantwoorden. Het bewijs voor de afgeleide van de sinusfunctie dat hij als voorbeeld heeft gekregen is overigens ook slecht opgeschreven, dus als hij het daarvan moet hebben ...quote:Op maandag 23 juni 2014 23:15 schreef netchip het volgende:
[..]
Volgens mij bedoelen ze met aantonen wat anders dan met bewijzen. Ook al een paar keer over gestruikeld.


Nou omdat ik gek ben:
Te bewijzen: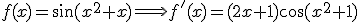
Gegeven: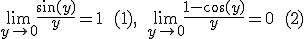
Definieer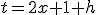 en merk op dat
en merk op dat 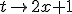 als
als 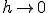 en
en 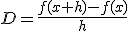
Hier begint het bewijs, voor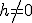 :
:
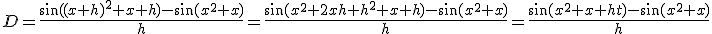
Een standaard goniometrische identiteit geeft:
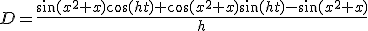
Wat te splitsen valt in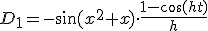 en
en 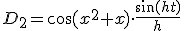
Vermenigvuldigen van beide expressies met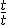 geeft
geeft
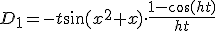 en
en 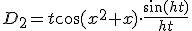
Wanneer we de limiet nemen van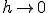 en gebruik maken van
en gebruik maken van 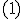 en
en  met
met 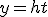 concluderen we dat
concluderen we dat 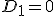 en dat
en dat 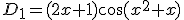
Alles te samen:
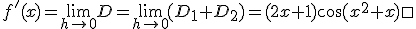
Te bewijzen:
Gegeven:
Definieer
Hier begint het bewijs, voor
Een standaard goniometrische identiteit geeft:
Wat te splitsen valt in
Vermenigvuldigen van beide expressies met
Wanneer we de limiet nemen van
Alles te samen:


Zoals ik al had opgemerkt gaat het een stuk eenvoudiger met de formule van Simpson voor het verschil van twee sinussen. Je hebt dan namelijkquote:
f(x + h) − f(x) = sin(x2 + 2xh + h2 + x + h) − sin(x2 + x) = 2·sin(½h(2x + 1 + h))·cos(x2 + x + xh + ½h2 + ½h)
Dan is het nog slechts een kwestie van teller en noemer van het differentiequotiënt (f(x + h) − f(x))/h vermenigvuldigen met ½·(2x + 1 + h) en de limiet nemen voor h → 0 en je hebt f'(x) = (2x + 1)·cos(x2 + x), QED.
[ Bericht 0% gewijzigd door Riparius op 24-06-2014 18:32:48 ]


Je hebt natuurlijk volkomen gelijk, dat is inderdaad de simpelste manier. Maar eerlijk gezegd kende ik jouw (tutoyeren lijkt me OK?) formule niet. Dat terwijl de som/verschil formules een stuk bekender zijn.quote:Op dinsdag 24 juni 2014 17:01 schreef Riparius het volgende:
[..]
Zoals ik al had opgemerkt gaat het een stuk eenvoudiger met de formule van Simpson voor het verschil van twee sinussen. Je hebt dan namelijk
f(x+h) − f(x) = sin(x2 + 2xh + h2 + x + h) − sin(x2 + x) = 2·sin(½h(2x + 1 + h))·cos(x2 + x + xh + ½h2 + ½h)
Dan is het nog slechts een kwestie van teller en noemer van het differentiequotiënt (f(x+h) − f(x))/h vermenigvuldigen met (2x + 1 + h) en de limiet nemen voor h → 0 en je hebt f'(x) = (2x + 1)·cos(x2 + x), QED.
Er zijn altijd meerdere wegen naar Rome, zeker in de wiskunde, maar de beste weg, naar mijn mening, is de weg die je kent.


Dat is het leuke van wiskunde, het kan altijd anders, en vaak eenvoudiger. De formules van Simpson worden in elementaire leerboeken voor differentiaalrekening vaak gebruikt om te bewijzen dat d(sin(x))/dx = cos(x) resp. d(cos(x))/dx = −sin(x) en dat ligt ook wel voor de hand omdat je in de teller van je differentiequotiënt een verschil van twee sinussen resp. cosinussen hebt. De formules van Simpson zijn trouwens eenvoudig af te leiden uit de additietheorema's. Je hebtquote:Op dinsdag 24 juni 2014 17:08 schreef Novermars het volgende:
[..]
Je hebt natuurlijk volkomen gelijk, dat is inderdaad de simpelste manier. Maar eerlijk gezegd kende ik jouw (tutoyeren lijkt me OK?) formule niet. Dat terwijl de som/verschil formules een stuk bekender zijn.
Er zijn altijd meerdere wegen naar Rome, zeker in de wiskunde, maar de beste weg, naar mijn mening, is de weg die je kent.
sin(α + β) = sin α·cos β + cos α·sin β
sin(α − β) = sin α·cos β − cos α·sin β
Aftrekken van de leden van de tweede identiteit van de leden van de eerste identiteit geeft
sin(α + β) − sin(α − β) = 2·cos α·sin β
Stel nu α + β = θ en α − β = φ, dan is α = ½(θ + φ) en β = ½(θ − φ) en je hebt
sin θ − sin φ = 2·cos½(θ + φ)·sin½(θ − φ)
Op volkomen analoge wijze kun je ook identiteiten afleiden voor het verschil van twee cosinussen en voor de som van twee sinussen of cosinussen.
[ Bericht 0% gewijzigd door Riparius op 24-06-2014 18:17:26 ]


Hey,
Heeft iemand misschien een PDF met de antwoorden van Stewart Calculus, Early Transcendentals 7E? Ik heb namelijk alleen het boek (in PDF vorm).
netchip
Heeft iemand misschien een PDF met de antwoorden van Stewart Calculus, Early Transcendentals 7E? Ik heb namelijk alleen het boek (in PDF vorm).
netchip


Ik haalde de antwoorden voor dat boek altijd hier vandaan: http://www.slader.com/tex(...)dentals-7th-edition/.quote:Op donderdag 26 juni 2014 14:52 schreef netchip het volgende:
Hey,
Heeft iemand misschien een PDF met de antwoorden van Stewart Calculus, Early Transcendentals 7E? Ik heb namelijk alleen het boek (in PDF vorm).
netchip
Daarnaast staat ook een deel van de antwoorden helemaal achterin het boek.


quote:Op donderdag 26 juni 2014 15:23 schreef Ensemble het volgende:
[..]
Ik haalde de antwoorden voor dat boek altijd hier vandaan: http://www.slader.com/tex(...)dentals-7th-edition/.
Daarnaast staat ook een deel van de antwoorden helemaal achterin het boek.
f(x) kan je echter versimpelen tot:
Dan is f(x) toch gelijk aan g(x)?


Nee, niet helemaal, want f(x) is niet gedefinieerd voor x = 1. De grafiek van f is dan ook een rechte lijn met een 'gaatje' erin bij x = 1. Zoiets heet een ophefbare discontinuïteit. We kunnen het 'gaatje' namelijk dicht maken door aanvullend nog f(1) = 1 te definiëren.quote:Op donderdag 26 juni 2014 16:36 schreef netchip het volgende:
[..]en g(x) = x zijn toch hetzelfde? Op internet staat dat het domein hetzelfde moet zijn en f(x) = g(x) moet gelden voor alle voorkomende waardes in dat domein.
f(x) kan je echter versimpelen tot:dus f(x) = x.
Dan is f(x) toch gelijk aan g(x)?


Ah, OK.quote:Op donderdag 26 juni 2014 16:42 schreef Riparius het volgende:
[..]
Nee, niet helemaal, want f(x) is niet gedefinieerd voor x = 1. De grafiek van f is dan ook een rechte lijn met een 'gaatje' erin bij x = 1. Zoiets heet een ophefbare discontinuïteit. We kunnen het 'gaatje' namelijk dicht maken door aanvullend nog f(1) = 1 te definiëren.
Andere vraag, deze is misschien een beetje triest, maar ik zie hem echt niet.
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |
