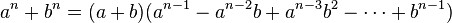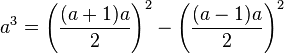SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!
Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).
Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...
OP
Handig:
Riparius heeft ooit een PDF geschreven over goniometrische identiteiten. Deze kun je hier downloaden:
www.mediafire.com/view/?2b214qltc7m3v0d
De manier waarop je dit formuleert geeft mooi je begripsverwarring weer: machtsverheffen is echt iets anders dan vermenigvuldigen met een bepaalde factor. Als je hebtquote:Op woensdag 10 juli 2013 10:00 schreef wiskundenoob het volgende:
Sorry, had het moeten weten dat je niet zomaar bij alle termen met machten mag vermenigvuldigen.
a + b = c
en je hebt een getal p ≠ 0, dan is dit equivalent met
ap + bp = cp
maar uit a + b = c volgt dan niet dat
ap + bp = cp
Immers, als dit wel zo was, dan zou je met p = 2 hebben
a2 + b2 = c2 = (a + b)2
en dit klopt in het algemeen niet, omdat (a + b)2 = a2 + 2ab + b2. Het dubbele product 2ab zorgt ervoor dat a2 + b2 in het algemeen niet hetzelfde is als (a + b)2. Dat zou alleen opgaan als 2ab = 0 zou zijn, en dat is alleen zo als hetzij a = 0 hetzij b = 0.
Het is van het grootste belang dat je in ieder geval de volgende merkwaardige producten van buiten kent en dat je deze bij allerlei algebraïsche herleidingen ook steeds kunt herkennen en kunt toepassen:
(a + b)2 = a2 + 2ab + b2
(a − b)2 = a2 − 2ab + b2
(a + b)(a − b) = a2 − b2
Het gaat hier steeds om de vermenigvuldiging van tweetermen die uit een som (a + b) of een verschil (a − b) van twee grootheden bestaan. Vermenigvuldiging van tweetermen komt erg vaak voor en met de tweetermen (a + b) en (a − b) kun je precies de bovenstaande drie producten vormen. Eigenlijk vier, maar (a − b)(a + b) is uiteraard hetzelfde als (a + b)(a − b) omdat vermenigvuldiging commutatief is.
Belangrijk bij alle identiteiten, en dus ook bij deze merkwaardige producten, is dat je ze zowel van links naar rechts als van rechts naar links kunt herkennen en toepassen. Dus, als je ergens p2 + 2pq + q2 tegenkomt, dan moet je onmiddellijk herkennen dat dit hetzelfde is als (p + q)2. En als je x2 − 6x + 9 ziet staan, dan moet je direct herkennen dat dit hetzelfde is als (x − 3)2.
Om deze identiteiten beter te begrijpen en te onthouden, kan het helpen om ze te visualiseren. Als a en b positieve getallen zijn, dan stelt (a + b)2 meetkundig de oppervlakte voor van een vierkant met zijde a + b. Dit vierkant is opgebouwd uit twee kleinere vierkanten met zijde a resp. zijde b, maar ook uit twee rechthoeken met afmeting a bij b, en dus oppervlakte ab, zodat de totale oppervlakte van het vierkant gelijk is aan a2 + 2ab + b2 zoals je hier kunt zien:
Bron
Het is ook mogelijk op deze manier de techniek van het kwadraatafsplitsen voor het oplossen van vierkantsvergelijkingen te visualiseren. Stel dat we de volgende vergelijking hebben:
x2 + 10x = 39
Wat men nu in de oudheid deed was dit opvatten als een vierkant met een onbekende zijde x en een rechthoek van 10 bij x die samen een oppervlakte van 39 eenheden moeten hebben.
De rechthoek van 10 bij x kunnen we verdelen in twee kleinere rechthoeken van 5 bij x die we met de zijde met lengte x tegen twee aangrenzende zijden van het vierkant met zijde x kunnen leggen. Dan krijgen we een L-vormige figuur, zoals je kunt zien. Deze figuur kunnen we aanvullen tot een groot vierkant door er nog een vierkant van 5 bij 5 bij te plaatsen (aangegeven met de stippellijnen in het plaatje). De totale oppervlakte van het grote vierkant wordt dan 39 + 25 = 64, zodat de zijde van het grote vierkant dus 8 moet zijn, want 8·8 = 64. Maar we zien ook dat de zijde van het grote vierkant x + 5 is, zodat dus x = 3 moet zijn.
Uiteraard vind je met deze antieke meetkundige methode alleen de positieve oplossing van de vergelijking, en niet de negatieve oplossing x = −13. Maar dit laat mooi het principe zien van het completeren van het vierkant (completing the square) en je ziet ook waarom kwadratische vergelijkingen nog altijd vierkantsvergelijkingen worden genoemd. En nu begrijp je hopelijk ook beter waarom je bij het oplossen van een vierkantsvergelijking via kwadraatafsplitsing - als althans de kwadratische coëfficiënt één is - de coëfficiënt van x halveert en hier weer het kwadraat van neemt om dit vervolgens bij beide leden op te tellen. Zie verder hier voor meer bijzonderheden.
[ Bericht 0% gewijzigd door Riparius op 10-07-2013 17:48:50 ]
Uh, klopt dat eerste plaatje wel? Waarom is a2 groter dan b2? Waarom zijn a en b niet even groot?
[ Bericht 14% gewijzigd door wiskundenoob op 11-07-2013 14:50:51 ]
[ Bericht 14% gewijzigd door wiskundenoob op 11-07-2013 14:50:51 ]
Ehhh, omdat men dat a priori dient te stellen om de herkomst en afleiding van die merkwaardig product formules inzichtelijk te maken mss? Stel dat a en b idd even groot zouden zijn dan zou je onmiddelijk kunnen stellen:quote:Op donderdag 11 juli 2013 14:27 schreef wiskundenoob het volgende:
Uh, klopt dat eerste plaatje wel? Waarom is a2 groter dan b2? Waarom zijn a en b niet even groot?
a=b => a+b <=> 2a <=> 2b .
(a+b)2 = a2 + 2ab + b2 .
Maar omdat a=b kan je ook gelijk opschrijven:
a2 + 2*a*a + a2 <=> b2 + 2*b*b + b2 <=> 4a2 <=> 4b2
Op eenzelfde manier is aan te tonen dat (a-b)2 = 0 als a=b geldt.
Heb het al begrepen.quote:
[..]
Ehhh, omdat men dat a priori dient te stellen om de herkomst en afleiding van die merkwaardig product formules inzichtelijk te maken mss? Stel dat a en b idd even groot zouden zijn dan zou je onmiddelijk kunnen stellen:
a=b => a+b <=> 2a <=> 2b .
(a+b)2 = a2 + 2ab + b2 .
Maar omdat a=b kan je ook gelijk opschrijven:
a2 + 2*a*a + a2 <=> b2 + 2*b*b + b2 <=> 4a2 <=> 4b2
Op eenzelfde manier is aan te tonen dat (a-b)2 = 0 als a=b geldt.
Hier ook een paper van een masterstudent waarin de formule van Cardano op soortgelijke (maar natuurlijk wat ingewikkeldere wijze) wordt afgeleid.quote:
Trouwens, ik zoek nog wat opgaven om bewijzen mee te oefenen. Ik heb wel putnam problemen gevonden, maar veel daarvan zijn toch wat te moeilijk voor me. Ik begrijp de te bewijzen stelling wel, maar ik kom eigenlijk nooit uit de bewijzen. Iemand een idee?
Ik ken dat stuk wel, maar ik vind het niet zo goed, zowel inhoudelijk als didactisch niet. Het begint al meteen bij de eerste alinea, waar de auteur de lezer vraagt of deze er wel eens over nagedacht heeft hoe de vergelijkingquote:
[..]
Hier ook een paper van een masterstudent waarin de formule van Cardano op soortgelijke (maar natuurlijk wat ingewikkeldere wijze) wordt afgeleid.
x3 + 3x2 + 6x + 8 = 0
algebraïsch kan worden opgelost. Dit is een heel slecht voorbeeld, want dergelijke vergelijkingen werden vroeger vaak als oefening in het ontbinden in factoren gegeven. Oplossen van deze vergelijking zonder kennis van de theorie van de kubische vergelijkingen is een koud kunstje omdat je hebt 3x2 + 6x = 3x(x + 2) en x3 + 8 = x3 + 23 = (x + 2)(x2 − 2x + 4) zodat we dus hebben
(x + 2)(x2 + x + 4) = 0
Er staan nogal wat onjuistheden in, zoals de bewering dat Al-Khwarizmi de eerste was die de techniek van kwadraatafsplitsing toepaste. Dat is niet zo, want ca. 1000 jaar eerder werd de techniek al gebruikt door de Grieken, en nog weer zo'n anderhalf millennium eerder (!) was de techniek ook al bekend bij de Babyloniërs, zie hier.
Interessant is dat de Babyloniërs een iets andere methode gebruikten dan de techniek die nu gewoonlijk onder completing the square wordt verstaan. Een bekend voorbeeld is het vraagstuk over een rechthoekig stuk land waarvan de lengte 20 eenheden groter is dan de breedte terwijl de oppervlakte 800 vierkante eenheden bedraagt en waarbij gevraagd wordt de afmetingen van het stuk land te bepalen.
Dit vraagstuk werd opgelost door de helft van het verschil tussen lengte en breedte te nemen, zijnde 10 eenheden, en een strook van deze breedte van de lengte af te halen en aan de breedte toe te voegen. Hierdoor verkrijgen we een L-vormig stuk land dat bestaat uit een vierkant waarvan de zijde het gemiddelde is van de lengte en breedte van het oorspronkelijke stuk land en waaraan een vierkant ontbreekt met een zijde gelijk aan het halve verschil tussen de lengte en breedte van het oorspronkelijke stuk land. Aangezien het L-vormige stuk land dezelfde oppervlakte heeft als het oorspronkelijke rechthoekige stuk land, 800 vierkante eenheden, en het ontbrekende vierkant een oppervlakte heeft van 100 vierkante eenheden, dus samen 900 vierkante eenheden, volgt zo dat het gemiddelde van de gezochte lengte en breedte 30 eenheden bedraagt. De afmetingen van het rechthoekige stuk land bedragen dus 40 bij 20 eenheden.
We kunnen deze werkwijze als volgt vertalen naar een algebraïsche oplossing van het vraagstuk. Noem de gezochte breedte van het stuk land x, dan is de lengte van het stuk land x + 20, en aangezien de oppervlakte 800 bedraagt hebben we dan
x(x + 20) = 800
Het gemiddelde van x en x + 20 is x + 10, en we kunnen nu schrijven x = (x + 10) − 10 en x + 20 = (x + 10) + 10, zodat we de vergelijking kunnen herschrijven als
((x + 10) − 10)((x + 10) + 10) = 800
Nu hebben we het linkerlid omgevormd tot een product van het verschil en de som van twee grootheden, zodat we de vergelijking nu met behulp van het merkwaardig product (a − b)(a + b) = a2 − b2 kunnen herschrijven als
(x + 10)2 − 102 = 800
zodat
(x + 10)2 = 900
waaruit volgt
x = 20 ∨ x = −40
Uiteraard voldoet voor het vraagstuk alleen de positieve oplossing. Deze methode van oplossen van een vierkantsvergelijking wordt wel de Babylonische methode genoemd. Hier wordt dus gebruik gemaakt van het merkwaardig product (a − b)(a + b) = a2 − b2 om het linkerlid te herleiden tot een verschil van twee kwadraten, terwijl bij de gangbare methode gebruik wordt gemaakt van het merkwaardig product (a ± b)2 = a2 ± 2ab + b2 om het linkerlid van de kwadratische vergelijking te completeren tot een volkomen kwadraat.
De (gemoderniseerde) weergave van Bombelli's behandeling van de kubische vergelijking x3 − 15x = 4 is niet juist, Bombelli schreef de oplossing x = 4 namelijk niet als een verschil maar als een som van twee derdemachtswortels uit 2 + √−121 resp. 2 − √−121.
Verder is de notatie i voor √−1 niet ingevoerd door Bombelli, maar pas twee eeuwen later door Euler, die de notatie voor het eerst gebruikte in een paper uit 1777, dat echter pas in 1794 (postuum) werd gepubliceerd. Enkele jaren later, in 1801, introduceerde ook Gauss de notatie i voor √−1, waarbij niet duidelijk is of hij dit onafhankelijk van Euler deed.
Ik mis in het stuk een bespreking van de goniometrische oplossingsmethode voor het geval de kubische vergelijking drie (verschillende) reële wortels heeft. Anders dan de auteur lijkt te willen suggereren is het in dit geval (casus irreducibilis) namelijk in het algemeen niet mogelijk gebruik te maken van de formules van Cardano om langs algebraïsche weg een oplossing te vinden van de kubische vergelijking.
Voor de afleiding van de abc-formule wordt uitgegaan van een afleiding van de pq-formule waaruit door een substitutie p = b/a en q = c/a dan de abc-formule wordt afgeleid. Veel eleganter is echter de directe herleiding van de abc-formule met behulp van de methode van Sridhara. Dit is een gemiste kans omdat het de mogelijkheid had geboden om kwadraatafsplitsing ook te behandelen in het algemene geval waarin de kwadratische coëfficiënt niet gelijk is aan 1 zonder daarbij de vergelijking eerst te herleiden tot de gedaante x2 + px + q = 0.
Geef eens wat voorbeelden van stellingen die je denkt te begrijpen maar waarvan je niet zelf een bewijs kunt verzinnen en (correct) op kunt schrijven.quote:Trouwens, ik zoek nog wat opgaven om bewijzen mee te oefenen. Ik heb wel putnam problemen gevonden, maar veel daarvan zijn toch wat te moeilijk voor me. Ik begrijp de te bewijzen stelling wel, maar ik kom eigenlijk nooit uit de bewijzen. Iemand een idee?
[ Bericht 0% gewijzigd door Riparius op 15-07-2013 04:02:22 ]
wtfquote:
[..]
Hier ook een paper van een masterstudent waarin de formule van Cardano op soortgelijke (maar natuurlijk wat ingewikkeldere wijze) wordt afgeleid.
Trouwens, ik zoek nog wat opgaven om bewijzen mee te oefenen. Ik heb wel putnam problemen gevonden, maar veel daarvan zijn toch wat te moeilijk voor me. Ik begrijp de te bewijzen stelling wel, maar ik kom eigenlijk nooit uit de bewijzen. Iemand een idee?
dat is een master thesis!
Haha inderdaadquote:
. Het had ook een matig profielwerkstuk kunnen zijn. Ik hoop dat je hiermee geen wiskunde master kan afronden, maar misschien een education master of zo. Het moet een soort leermethode voor middelbare scholieren voorstellen denk ik.
Zelfs voor een educational master vind ik het nogal erg matig. Er staat nou niet echt hele moeilijke dingen in. Ik denk dat iedere beta master of bachelor student dit kan schrijven.quote:Op zaterdag 13 juli 2013 10:42 schreef thenxero het volgende:
[..]
Haha inderdaad
Ja, klopt. Van die master had ik ook al niet zo'n hoge pet opquote:Op zaterdag 13 juli 2013 10:53 schreef Dale. het volgende:
[..]
Zelfs voor een educational master vind ik het nogal erg matig. Er staat nou niet echt hele moeilijke dingen in. Ik denk dat iedere beta master of bachelor student dit kan schrijven.
.
Ben ik helemaal met je eens, ik vond het alleen wel mooi om te zien dat de formule ook geometrisch afgeleid kan worden. Bij infi heb ik het geleerd om met een aantal substituties te doen die totaal niet voor de hand liggen, dan vind ik deze manier toch mooier.quote:
[..]
Ik ken dat stuk wel, maar ik vind het niet zo goed, zowel inhoudelijk als didactisch niet. Het begint al meteen bij de eerste alinea, waar de auteur de lezer vraagt of deze er wel eens over nagedacht heeft hoe de vergelijking
x3 + 3x2 + 6x + 8 = 0
[...]
O, ik heb er geloof ik nog wel wat liggen, maar dat zijn dus voornamelijk putnam-problemen.quote:Geef eens wat voorbeelden van stellingen die je denkt te begrijpen maar waarvan je niet zelf een bewijs kunt verzinnen en (correct) op kunt schrijven.
Zoals (maar die is volgens mij dan weer achterlijk moeilijk) deze:
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Oh, laat maar. Ik ben net deze site tegengekomen. De makkelijkste daarvan zijn denk ik wel een goede uitdagingEr stond 'project', ik wist niet zeker of dat een thesis was of niet, maar ik vreesde inderdaad al dat het een thesis was... Anyway, het lijkt me ook ontzettend moeilijk om een goede thesis te schrijven, dus als ik dat ooit nog moet gaan doen kom ik misschien ook met zoiets op de proppenquote:
quote:
[..]
Ben ik helemaal met je eens, ik vond het alleen wel mooi om te zien dat de formule ook geometrisch afgeleid kan worden. Bij infi heb ik het geleerd om met een aantal substituties te doen die totaal niet voor de hand liggen, dan vind ik deze manier toch mooier.
[..]
O, ik heb er geloof ik nog wel wat liggen, maar dat zijn dus voornamelijk putnam-problemen.
Zoals (maar die is volgens mij dan weer achterlijk moeilijk) deze:Bij de UU staat geloof ik 47 ECTS voor je masterthesis. Dan kan je ook wel wat meer dan dat verwachten. Met een dergelijke scriptie ga je het ook echt niet redden, als je even het niveau van wat echte scripties bekijkt: http://studenttheses.libr(...)Sciences&language=nl .SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Oh, laat maar. Ik ben net deze site tegengekomen. De makkelijkste daarvan zijn denk ik wel een goede uitdaging
[..]
Er stond 'project', ik wist niet zeker of dat een thesis was of niet, maar ik vreesde inderdaad al dat het een thesis was... Anyway, het lijkt me ook ontzettend moeilijk om een goede thesis te schrijven, dus als ik dat ooit nog moet gaan doen kom ik misschien ook met zoiets op de proppen
Kan iemand mij uitleggen wat -b/a en c/a betekent bij een kwadratische vergelijking.
[ Bericht 2% gewijzigd door wiskundenoob op 13-07-2013 19:11:45 ]
[ Bericht 2% gewijzigd door wiskundenoob op 13-07-2013 19:11:45 ]
Meestal staat de - staat voor aftrekken, de / voor delen, en a,b voor de coëfficienten van x^2 resp. x, en c de constante term.quote:
Kan iemand mij uitleggen wat -b/a en a/c betekent bij een kwadratische vergelijking.
Ja, maar wat reken je dan uit?quote:
[..]
Meestal staat de - staat voor aftrekken, de / voor delen, en a,b voor de coëfficienten van x^2 resp. x, en c de constante term.
Dingen afkraken is nogal een kansloze aangelegenheid als je niet eens in staat bent om even op te zoeken waar dat verslag nu daadwerkelijk van is.quote:
[..]
Ja, klopt. Van die master had ik ook al niet zo'n hoge pet op
Het is namelijk onderdeel van een 10 EC vak :http://www.studiegids.sci(...)ourses/course/29529/
Ik kraak het niet af, en ik zei al dat je er misschien een education master mee kan afronden. Desondanks ontstijgt het nauwelijks het pws niveau.quote:
[..]
Zoiets afkraken is nogal een kansloze aangelegenheid als je niet eens in staat bent om even op te zoeken waar dat verslag nu daadwerkelijk van is.
Het is namelijk onderdeel van een 10 EC vak :http://www.studiegids.sci(...)ourses/course/29529/
Ik zeg ook niet dat het een briljant verslag is (alleen al het aantal spelfouten...). Misschien had ik beter Dale kunnen quoten. Overigens is het een onderwijsmodule, dus kunt je moeilijk iets op master niveau gaan maken.quote:
[..]
Ik kraak het niet af, en ik zei al dat je er misschien een education master mee kan afronden. Desondanks ontstijgt het nauwelijks het pws niveau.
Daarnaast was mijn PWS van hoger niveau; dat ging over Blackjack & Poker i.c.m. kansrekenen
.
Dat bedoel ik dusquote:
[..]
Ik zeg ook niet dat het een briljant verslag is (alleen al het aantal spelfouten...). Misschien had ik beter Dale kunnen quoten. Overigens is het een onderwijsmodule, dus kunt je moeilijk iets op master niveau gaan maken.
Daarnaast was mijn PWS van hoger niveau; dat ging over Blackjack & Poker i.c.m. kansrekenen
. Het hoeft bij zo'n master natuurlijk ook geen technisch hoogstandje te zijn. Maar je mag wel verwachten dat het historisch correct is, met goede bronnen en zonder spelfouten. Bovendien laat de opbouw ook het een en ander te wensen over. En dat ik niet zo'n hoge pet op heb van die master is (misschien niet geheel terecht) gebaseerd op de lesmethodes die ik tegenkom op middelbare scholen. Ik ga er dan even vanuit dat mensen die lesmethodes schrijven wel een master in education hebben. Toch kom ik aan de lopende band didactisch onverantwoorde sommen tegen. Als die master van hoog niveau is dan zou dat niet moeten kunnen.
Ook heb ik een keer gelezen in een blad (kan me de bron niet meer herinneren), dat het niveau van de education master zwaar onder druk stond.
Alleen c is constant, denk ik.quote:
[..]
En toen?
a, b en c zijn gewoon constanten.
Kun je misschien uitleggen waarom je dat denkt en kun je het volledige plaatje geven? Want hier kan uiteraard niemand wat mee.quote:
Bij een kwadratische vergelijking is c volgens mij een constante en het staat ook in de post van thenxero.quote:
[..]
Kun je misschien uitleggen waarom je dat denkt en kun je het volledige plaatje geven? Want hier kan uiteraard niemand wat mee.
Bijv.
x^2 + 10x - 39 = 0
c = -39
[ Bericht 2% gewijzigd door wiskundenoob op 13-07-2013 18:51:33 ]
Heb je het nu over de abc-formule of zo? c = -39 is nogal een rare statement, want er komt verder geen c voor in je post.quote:
[..]
Bij een kwadratische vergelijking is c volgens mij een constante en het staat ook in de post van thenxero.
Bijv.
x^2 + 10x - 39 = 0
c = -39
Voor de abc-formule kun je x2 + 10x - 39 in ieder geval zien als ax2 + bx + c. Waarbij a=1, b=10 en c=-39.
Maar nogmaals, het is handig als je het volledige verhaal post...
[ Bericht 0% gewijzigd door Thormodo op 13-07-2013 19:00:32 ]
Ik heb wel een vermoeden waar die het over heeft. Maar zolang hij geen heldere vraag formuleert ga ik er niet meer op in.
Je mag blij zijn dat mensen je willen helpen. Maar als je er zelf geen moeite in steekt, krijg je ook geen moeite terug.
Je mag blij zijn dat mensen je willen helpen. Maar als je er zelf geen moeite in steekt, krijg je ook geen moeite terug.
Ok, dat valt dan wel weer meequote:
[..]
Dingen afkraken is nogal een kansloze aangelegenheid als je niet eens in staat bent om even op te zoeken waar dat verslag nu daadwerkelijk van is.
Het is namelijk onderdeel van een 10 EC vak :http://www.studiegids.sci(...)ourses/course/29529/
Als je nagaat hoe weinig moeite je voor sommige vakken van 7,5 ects hoeft te doen
Klinkt interessantquote:
[..]
Ik zeg ook niet dat het een briljant verslag is (alleen al het aantal spelfouten...). Misschien had ik beter Dale kunnen quoten. Overigens is het een onderwijsmodule, dus kunt je moeilijk iets op master niveau gaan maken.
Daarnaast was mijn PWS van hoger niveau; dat ging over Blackjack & Poker i.c.m. kansrekenen
Kan je dit toelichten met wat concrete voorbeeldjes? Ik twijfel er niet aan dat je gelijk hebt maar het is handig om het wat concreter te maken.quote:
[..]
Dat bedoel ik dus
En dat ik niet zo'n hoge pet op heb van die master is (misschien niet geheel terecht) gebaseerd op de lesmethodes die ik tegenkom op middelbare scholen. Ik ga er dan even vanuit dat mensen die lesmethodes schrijven wel een master in education hebben. Toch kom ik aan de lopende band didactisch onverantwoorde sommen tegen. Als die master van hoog niveau is dan zou dat niet moeten kunnen.
Ook heb ik een keer gelezen in een blad (kan me de bron niet meer herinneren), dat het niveau van de education master zwaar onder druk stond.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Wat ik in veel boeken zie is het volgende. Eerst geven ze een "oriënterende som". Het idee is daar dat je gaat nadenken over iets voordat het wordt uitgelegd. In principe is daar nog niks mis mee (alhoewel het niet mijn smaak is, maar dat terzijde). Vervolgens staat er in een "theorie-vakje" (vaak een vrolijk kleurtje met een vrolijk mannetje ernaast) hetgeen wat je hebt uitgevonden in de oriënterende som, maar dan als algemene waarheid.quote:
[..]
Kan je dit toelichten met wat concrete voorbeeldjes? Ik twijfel er niet aan dat je gelijk hebt maar het is handig om het wat concreter te maken.
Ze laten je bijvoorbeeld f(x)=2x primitiveren tot F(x)=x². Dan mag je F(1)-F(0) uitrekenen en krijg je dus 1 als uitkomst. Je moet ook even herkennen dat het gewoon een driehoekje is en de oppervlakte dus 2*1*1/2 = 1 is. Je ziet dus dat in dit geval de primitieves op 1 en 0 van elkaar afgetrokken gelijk is aan de oppervlakte onder de functie op [0,1]. Vervolgens staat eronder in het "theorie-vakje" simpelweg: De oppervlakte onder de grafiek f van a tot b bepaal je door F(b)-F(a) te berekenen.
Ja, dat is waar. Maar het staat er alsof je met één voorbeeld bewezen hebt dat dat zo is. Alsof je dom bent als je dan nog niet snapt waarom dat altijd waar is. Voor scholieren kan dat best leiden tot onzekerheid, want je weet niet meer wanneer je iets niet snapt of wanneer je het simpelweg niet kán snappen, omdat het niet is uitgelegd.
Een ander voorbeeld. Laatst kwam ik een 'bewijs' tegen waarom de afgeleide van ln(x) gelijk is aan 1/x. Dat ging ongeveer zo (uit mijn hoofd):
Stel y=ex, oftewel x=ln(y). Dan
(1)
Dus ook (?!)
Verder hebben we
Dus
Dus
(Hmm, het originele bewijs was nog erger, want daar werden x en y midden in het bewijs omgewisseld. Totaal overbodig en erg verwarrend. Ik moest het ook drie keer lezen. Ik kan echter niet reproduceren waar ze die wisseltruc deden, dus ik laat het maar zo.)
De (?!) stap vond ik nogal dubieus. Het vereist op zijn minst een rechtvaardiging als je claims maakt als
Bovendien, waarom nou niet gewoon op een heldere manier de kettingregel gebruiken? Ik zou het als volgt doen.
Merk op dat eln(x) = x. Beide kanten differentiëren naar x geeft met de kettingregel:
Dus
Klaar. Niet moeilijker maken dan dat het is!
En zo kan ik helaas nog wel even doorgaan. Nou, nog ééntje dan. Gegeven is een functie f(x) = e-x sin(x). Wat is de periode van deze functie? Beschouw nu g(x)=f(x)^2. Wat is de periode van g?
Nou dan is er alweer een probleem. Ten eerste werd periode in dat boek niet gedefinieerd, maar in mijn ogen is de periode het kleinste getal a zodanig dat f(x+a)=f(x), voor alle x in het domein. Dus wat is dan de periode
?
Hallo,
ik heb problemen met het begrijpen hoe ik een 'goodness of fit' doe met een Cox regression model. Ik heb via SPSS Cox-Snell residuals verkregen. Als ik papers raadpleeg (http://support.sas.com/re(...)dings13/431-2013.pdf , http://books.google.nl/bo(...)tribution%22&f=false )
dan zou ik een plot moeten krijgen waarbij op de x-axis de residuals staan, maar de y-axis is mij geheel onduidelijk.
Verder zou de residuals moeten lijken op een 'unit exponential distribution', maar ik kan nergens vinden wat de 'unit' toevoegt aan de exponential distribution.. mijn eigen interpretatie is dat het gewoon de exp. distr. is met lambda = 1.
Iemand die misschien toevallig iets af weet van proportional hazard models / cox regression?
Alvast bedankt!
ik heb problemen met het begrijpen hoe ik een 'goodness of fit' doe met een Cox regression model. Ik heb via SPSS Cox-Snell residuals verkregen. Als ik papers raadpleeg (http://support.sas.com/re(...)dings13/431-2013.pdf , http://books.google.nl/bo(...)tribution%22&f=false )
dan zou ik een plot moeten krijgen waarbij op de x-axis de residuals staan, maar de y-axis is mij geheel onduidelijk.
Verder zou de residuals moeten lijken op een 'unit exponential distribution', maar ik kan nergens vinden wat de 'unit' toevoegt aan de exponential distribution.. mijn eigen interpretatie is dat het gewoon de exp. distr. is met lambda = 1.
Iemand die misschien toevallig iets af weet van proportional hazard models / cox regression?
Alvast bedankt!
Sowieso vind ik heel het stelling-bewijs model een beetje, hoe zal ik het zeggen, ongepast (?) voor wiskunde-onderwijs. Een mooi of kort bewijs is vaak compleet wat anders dan een didactisch verantwoord verhaal, en ik zie liever een verhaal dat ik makkelijk onthoud dan een indrukwekkend bewijs, al is het alleen maar omdat ik na het eerste zelf eerder in staat ben zelf een bewijs te produceren.quote:
Het "definitie-stelling-bewijs verhaal" is essentieel voor wiskunde-onderwijs. Door al te veel in Jip- en Janneketaal te werken kan je uitleg op meerdere manieren interpreteren. Het beste werkt het volgens mij om alles zo exact mogelijk te houden en vervolgens met voorbeelden de theorie en de toepassingen te verduidelijken. Zijn kritiek ging echter veel verder dan dat.
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Volgens mij mis je compleet het punt van mijn post. Bovendien zijn bewijzen niet gemaakt om indruk te wekken, maar om een zo eenvoudig en precies mogelijke redenering te geven. En het lijkt me sterk dat je makkelijker gegoochel onthoudt, dan een simpel bewijsje wat precies voortbouwt op wat je al weet.quote:
[..]
Sowieso vind ik heel het stelling-bewijs model een beetje, hoe zal ik het zeggen, ongepast (?) voor wiskunde-onderwijs. Een mooi of kort bewijs is vaak compleet wat anders dan een didactisch verantwoord verhaal, en ik zie liever een verhaal dat ik makkelijk onthoud dan een indrukwekkend bewijs, al is het alleen maar omdat ik na het eerste zelf eerder in staat ben zelf een bewijs te produceren.
Bewijzen zijn niet bedoeld om indruk te wekken, maar vaak wordt er wel een zo kort mogelijk bewijs gegeven, waar je dan weer niet zoveel van leert. Een groot deel van mijn studieboeken en dictaten bestaat uit stellingen en bewijzen, en volgens mij kan de ruimte in veel gevallen beter gebruikt worden.quote:
[..]
Volgens mij mis je compleet het punt van mijn post. Bovendien zijn bewijzen niet gemaakt om indruk te wekken, maar om een zo eenvoudig en precies mogelijke redenering te geven. En het lijkt me sterk dat je makkelijker gegoochel onthoudt, dan een simpel bewijsje wat precies voortbouwt op wat je al weet.
Volgens mij is het meer een soort tik die veel wiskundigen hebben, om bij elke stelling een bewijs neer te zetten, ook al is het bewijs op zich niet zo leerzaam. Dan vind ik een 'bewijsschets' geven in veel gevallen nog mooier, omdat je studenten wel snel een idee geeft hoe het bewijs werkt, maar het nog steeds makkelijk leesbaar blijft.
Mijn post was inhoudelijk ook niet echt een reactie op jouw post, meer een licht gerelateerde ergernis die ik soms wel eens heb. Ik zal eens kijken of ik een voorbeeld kan vinden, dan kan ik het misschien wat duidelijker maken.
dan kan sneller; moet je alleen wel differentialen gehad hebbenquote:
[..]
Wat ik in veel boeken zie is het volgende. Eerst geven ze een "oriënterende som". Het idee is daar dat je gaat nadenken over iets voordat het wordt uitgelegd. In principe is daar nog niks mis mee (alhoewel het niet mijn smaak is, maar dat terzijde). Vervolgens staat er in een "theorie-vakje" (vaak een vrolijk kleurtje met een vrolijk mannetje ernaast) hetgeen wat je hebt uitgevonden in de oriënterende som, maar dan als algemene waarheid.
Ze laten je bijvoorbeeld f(x)=2x primitiveren tot F(x)=x². Dan mag je F(1)-F(0) uitrekenen en krijg je dus 1 als uitkomst. Je moet ook even herkennen dat het gewoon een driehoekje is en de oppervlakte dus 2*1*1/2 = 1 is. Je ziet dus dat in dit geval de primitieves op 1 en 0 van elkaar afgetrokken gelijk is aan de oppervlakte onder de functie op [0,1]. Vervolgens staat eronder in het "theorie-vakje" simpelweg: De oppervlakte onder de grafiek f van a tot b bepaal je door F(b)-F(a) te berekenen.
Ja, dat is waar. Maar het staat er alsof je met één voorbeeld bewezen hebt dat dat zo is. Alsof je dom bent als je dan nog niet snapt waarom dat altijd waar is. Voor scholieren kan dat best leiden tot onzekerheid, want je weet niet meer wanneer je iets niet snapt of wanneer je het simpelweg niet kán snappen, omdat het niet is uitgelegd.
Een ander voorbeeld. Laatst kwam ik een 'bewijs' tegen waarom de afgeleide van ln(x) gelijk is aan 1/x. Dat ging ongeveer zo (uit mijn hoofd):
Stel y=ex, oftewel x=ln(y). Dan
(1)
Dus ook (?!)
Verder hebben we
Dus
Dus
(Hmm, het originele bewijs was nog erger, want daar werden x en y midden in het bewijs omgewisseld. Totaal overbodig en erg verwarrend. Ik moest het ook drie keer lezen. Ik kan echter niet reproduceren waar ze die wisseltruc deden, dus ik laat het maar zo.)
De (?!) stap vond ik nogal dubieus. Het vereist op zijn minst een rechtvaardiging als je claims maakt als
Bovendien, waarom nou niet gewoon op een heldere manier de kettingregel gebruiken? Ik zou het als volgt doen.
Merk op dat eln(x) = x. Beide kanten differentiëren naar x geeft met de kettingregel:
Dus
Klaar. Niet moeilijker maken dan dat het is!
En zo kan ik helaas nog wel even doorgaan. Nou, nog ééntje dan. Gegeven is een functie f(x) = e-x sin(x). Wat is de periode van deze functie? Beschouw nu g(x)=f(x)^2. Wat is de periode van g?
Nou dan is er alweer een probleem. Ten eerste werd periode in dat boek niet gedefinieerd, maar in mijn ogen is de periode het kleinste getal a zodanig dat f(x+a)=f(x), voor alle x in het domein. Dus wat is dan de periode
f(x)=ln(x)
Stel ln(x)=t => x=e^t
Bereken dy/dx: d(ln(x))/dx = dt/d(et) = 1dt/etdt = 1dt/etdt = 1/et = 1/x
Vaak wordt ln(x) = ∫1x t-1dt geïntroduceerd als deze integraal en dan volgt direct uit de hoofdstelling van de integraalrekening dat d(ln(x))/dx = 1/x. Daarna kan dan exp(x) gedefinieerd worden als de inverse functie van ln(x) en volgt met de kettingregel ook gemakkelijk dat d(exp(x))/dx = exp(x).quote:
[..]
Een ander voorbeeld. Laatst kwam ik een 'bewijs' tegen waarom de afgeleide van ln(x) gelijk is aan 1/x. Dat ging ongeveer zo (uit mijn hoofd):
Dit ligt meer voor de hand dan de omgekeerde weg volgen en eerst de afgeleide van ax behandelen (met a > 0), want om aan te tonen dat d(ax)/dx = ln(a)·ax heb je sowieso natuurlijke logarithmen nodig en zou je ook eerst aan moeten tonen dat limh→0 (ah − 1)/h = ln(a).
Helemaal mee eens. limh→0 (ah − 1)/h = ln(a) werd ook nergens aangetoond.quote:
[..]
Vaak wordt ln(x) = ∫1x t-1dt geïntroduceerd als deze integraal en dan volgt direct uit de hoofdstelling van de integraalrekening dat d(ln(x))/dx = 1/x. Daarna kan dan exp(x) gedefinieerd worden als de inverse functie van ln(x) en volgt met de kettingregel ook gemakkelijk dat d(exp(x))/dx = exp(x).
Dit ligt meer voor de hand dan de omgekeerde weg volgen en eerst de afgeleide van ax behandelen (met a > 0), want om aan te tonen dat d(ax)/dx = ln(a)·ax heb je sowieso natuurlijke logarithmen nodig en zou je ook eerst aan moeten tonen dat limh→0 (ah − 1)/h = ln(a).
Overigens kan ik het wel met de hand uitrekenen, de primitieve is immers bekend. Maar even in mijn GR gegooid, het antwoord voldoet weinig aan de verwachtingen.
Fervent tegenstander van het korps lasergamers.
WolframAlpha snapt dit prima, maar jij voert het kennelijk verkeerd in, kijk maar hoe het wel werkt.quote:
Wat is er dan precies mis met mijn stukje LaTeX (of TeX, hoe die code ook mag heten)?quote:
[..]
WolframAlpha snapt dit prima, maar jij voert het kennelijk verkeerd in, kijk maar hoe het wel werkt.
| 1 | 1-4(\int_0^1(\sqrt{1-x^2})dx - 2\int_0^{1/2}(\sqrt{1-x^2})dx) |
Fervent tegenstander van het korps lasergamers.
Niets, en als ik dat invoer in WolframAlpha werkt het ook, dus kennelijk had je dan eerst iets anders.quote:Op woensdag 17 juli 2013 17:18 schreef Amoeba het volgende:
[..]
Wat is er dan precies mis met mijn stukje LaTeX (of TeX, hoe die code ook mag heten)?
[ code verwijderd ]
Amoeba, wat voor cijfer heb jij gekregen voor jouw PWS?
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Een 7 man. Ik voel me hard genaaid.quote:
Amoeba, wat voor cijfer heb jij gekregen voor jouw PWS?
Nu snap ik er ook niks meer van. Net kon hij er niet veel van maken.quote:
[..]
Niets, en als ik dat invoer in WolframAlpha werkt het ook, dus kennelijk had je dan eerst iets anders.
Fervent tegenstander van het korps lasergamers.
Zo'n havist had last minute 10 uur werk erin gestoken en ontvangt een 9. Ik heb hier tantoe hard voor na zitten denken en krijg een 7. Het leven is een partij oneerlijk.quote:
Fervent tegenstander van het korps lasergamers.
Je moet maar opzoeken hoeveel geld een theoretische wiskundige verdient voor het aantal uren dat hij van zijn leven erin stopt.quote:
[..]
Zo'n havist had last minute 10 uur werk erin gestoken en ontvangt een 9. Ik heb hier tantoe hard voor na zitten denken en krijg een 7. Het leven is een partij oneerlijk.
Hoe theoretischer een wiskundige is, hoe harder hij genaaid wordt.
Ik wil trouwens best je pws lezen, want nu ben ik wel benieuwd.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
De opgave is duidelijk, dat je met de discriminant moet werken ook. Maar waar halen ze die derde vergelijking vandaan? Het is namelijk geen herleiding, want als je ze plot krijgt je twee andere grafieken.
Gist is liefde, gist is leven. Vooral in een vagijn.
Beide kanten vermenigvuldigen met 2x+a.quote:
[ afbeelding ]
[ afbeelding ]
De opgave is duidelijk, dat je met de discriminant moet werken ook. Maar waar halen ze die derde vergelijking vandaan? Het is namelijk geen herleiding, want als je ze plot krijgt je twee andere grafieken.
Ohh, zo.quote:
[..]
Beide kanten vermenigvuldigen met 2x+a.
Bedankt.
Gist is liefde, gist is leven. Vooral in een vagijn.
Nog een vraagje. (Sorry, het is allemaal een beetje weggezakt de laatste tijd. )
Ik wil een breuk primitiveren;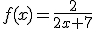
Dan krijg je sowieso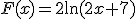
, maar ik heb het idee dat dit nog niet compleet is. Ik heb heel sterk de neiging om te concluderen dat je nog wat met die 
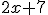moet doen, maar wat ook al weer?
)Ik wil een breuk primitiveren;
Dan krijg je sowieso
Gist is liefde, gist is leven. Vooral in een vagijn.
Je zit in de buurt. Als je de "primitieve" differentieert (met kettingregel!) dan zie je dat je niet de originele functie terugkrijgt: je zit er een constante naast.quote:
Nog een vraagje. (Sorry, het is allemaal een beetje weggezakt de laatste tijd.
Ik wil een breuk primitiveren;
Dan krijg je sowieso
Ah ja, differentiëren om de primitieve te controleren, dat is wel handig.quote:
[..]
Je zit in de buurt. Als je de "primitieve" differentieert (met kettingregel!) dan zie je dat je niet de originele functie terugkrijgt: je zit er een constante naast.
Dat ga ik dan even doen, nogmaals bedankt.
Gist is liefde, gist is leven. Vooral in een vagijn.
Ik ben mijn USB stick met het origineel kwijtgeraaktquote:
[..]
Je moet maar opzoeken hoeveel geld een theoretische wiskundige verdient voor het aantal uren dat hij van zijn leven erin stopt.
Hoe theoretischer een wiskundige is, hoe harder hij genaaid wordt.
Ik wil trouwens best je pws lezen, want nu ben ik wel benieuwd.
Dit is een van de laatste versies. Er kan dus nog ergens een typo ofzo instaan, maar het geeft een idee.
Je hebt DM.. Mijn naam en toenaam staan erbij namelijk.
Fervent tegenstander van het korps lasergamers.
Het enige wat je fout deed was die vermenigvuldiging met 2 ervoor zetten. Differentïeren van ln(2x+7) met de kettingregel geeft 1/(2x+7) * [2x+7]' = 1/(2x+7) * 2 = 2/(2x+7)quote:
Je kon dit direct zien doordat 2 de afgeleide is van 2x+7. Dat je dat direct herkent, daar willen ze uiteindelijk naartoe.
Fervent tegenstander van het korps lasergamers.
Ja, dat had ik me ook al bedacht.quote:
[..]
Het enige wat je fout deed was die vermenigvuldiging met 2 ervoor zetten. Differentïeren van ln(2x+7) met de kettingregel geeft 1/(2x+7) * [2x+7]' = 1/(2x+7) * 2 = 2/(2x+7)
Je kon dit direct zien doordat 2 de afgeleide is van 2x+7. Dat je dat direct herkent, daar willen ze uiteindelijk naartoe.
Het was alleen even weggezakt, maar nu moet de rest wel lukken (qua integreren dan).
Gist is liefde, gist is leven. Vooral in een vagijn.
[ Bericht 100% gewijzigd door Bram_van_Loon op 19-07-2013 14:00:23 ]
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik ben weer ergens op vastgelopen, gonio deze keer.
Hoe komen zij aan
?
Hoe komen zij aan
Gist is liefde, gist is leven. Vooral in een vagijn.
Bedoel je die bijna laatste gelijkheid?quote:
Ik ben weer ergens op vastgelopen, gonio deze keer.
[ afbeelding ]
[ afbeelding ]
Hoe komen zij aan
Daar kun je 0,5*cos(x)*(3 + sin(2x)) namelijk uitschrijven (dus zonder de haakjes om 3 + sin(2x)) en dan kun je zien dat er wat weg valt. Vervolgens kun je er weer haakjes omheen bouwen.
Oh, gewoon herleiden en dan ontbinden in factoren dus? Ik dacht dat het iets met de goniometrieregels had te maken.quote:
[..]
Bedoel je die bijna laatste gelijkheid?
Daar kun je 0,5*cos(x)*(3 + sin(2x)) namelijk uitschrijven (dus zonder de haakjes om 3 + sin(2x)) en dan kun je zien dat er wat weg valt. Vervolgens kun je er weer haakjes omheen bouwen.
Bedankt.
Gist is liefde, gist is leven. Vooral in een vagijn.
Even een vraagje over verzamelingenleer. Klopt het dat het supremum niets anders is dan de grootste bovengrens en het infinum de kleinste ondergrens?
Bijna goedquote:
Even een vraagje over verzamelingenleer. Klopt het dat het supremum niets anders is dan de grootste bovengrens en het infinum de kleinste ondergrens?
, het supremum is de kleinste bovengrens en infimum is de grootste ondergrens.
Dus bijvoorbeeld, [0,1) heeft geen maximum. (Want stel er is een maximum x. Dan geldt x < x+(1-x)/2 <1, tegenspraak.) Maar het supremum is 1. In dit geval is het infumum en het minimum 0.quote:
[..]
Bijna goed
Zo voelde ik me ook. Ik heb uiteindelijk een wiskundig getint PWS ingeleverd, maar het werd nagekeken door een biologiedocent, en die hield niet van wiskundequote:
Gelukkig uiteindelijk nog wel een 8 gekregen, maar ik hoorde van mensen dat ze in één dag een PWS in elkaar geflanst hebben en ook een 8 hadden.
Wolfram Alpha derpt soms, heb ik ook weleens last van gehad. Ik denk dat je browser opnieuw opstarten kan helpen. Ik kan me voorstellen dat ze verschillende servers hebben met verschillende versies software, en dat het daardoor komt.quote:[..]
Nu snap ik er ook niks meer van. Net kon hij er niet veel van maken.
Mensen die beweren er 1 dag aan gewerkt te hebben zijn van die nerdjes die stiekem al 2 jaar bezig zijn met voorbereiden.
Dan hebben ze het gewoon met flink wat knip- en plakwerk bij elkaar gesprokkeld vanaf internet. Een beetje docent ziet dat meteen, alleen al door de wisselende schrijfstijlen of het inconsequente gebruik van notaties of een gebrekkige opbouw van het geheel, maar waarschijnlijk zijn er ook veel docenten die de kantjes eraf lopen en het wel best vinden, of geen zin hebben zich erin te verdiepen omdat het buiten hun eigenlijke vakgebied ligt, en dan krijg je dit soort 'beoordelingen'.quote:
[..]
Gelukkig uiteindelijk nog wel een 8 gekregen, maar ik hoorde van mensen dat ze in één dag een PWS in elkaar geflanst hebben en ook een 8 hadden.
Ik denk het niet, heb er geen last van. WolframAlpha gebruikt inderdaad verschillende servers, maar ik heb nooit verschillen bemerkt. Wel is er het probleem dat de eerste paar karakters die je typt vaak niet doorkomen als je de hoofdpagina van WolframAlpha oproept en direct iets invoert. Als je dan niet oplet wat je precies invoert dan kan het inderdaad gemakkelijk gebeuren dat WolframAlpha de syntaxis niet begrijpt of verkeerd interpreteert.quote:[..]
Wolfram Alpha derpt soms, heb ik ook weleens last van gehad. Ik denk dat je browser opnieuw opstarten kan helpen. Ik kan me voorstellen dat ze verschillende servers hebben met verschillende versies software, en dat het daardoor komt.
Ja dat bedoelde ik, schreef het alleen verkeerd op. Bedankt in ieder geval.quote:
[..]
Bijna goed
Ja, afhankelijk van of de grenzen ook in de verzameling zitten zit het supremum/infinum dus wel/niet zelf in de verzameling. Bedankt voor de reactie.quote:
[..]
Dus bijvoorbeeld, [0,1) heeft geen maximum. (Want stel er is een maximum x. Dan geldt x < x+(1-x)/2 <1, tegenspraak.) Maar het supremum is 1. In dit geval is het infumum en het minimum 0.
Ik heb het maar één keer gehad (maar ik heb wolfram best vaak gebruikt), maar ik weet wel zeker dat ik het toen niet verkeerd heb ingetypt (ik had het toen van een link). Maargoed, voor hetzelfde geld ging er iets anders fout op de server, daar valt verder niet zoveel over te zeggen.quote:
Ik denk het niet, heb er geen last van. WolframAlpha gebruikt inderdaad verschillende servers, maar ik heb nooit verschillen bemerkt. Wel is er het probleem dat de eerste paar karakters die je typt vaak niet doorkomen als je de hoofdpagina van WolframAlpha oproept en direct iets invoert. Als je dan niet oplet wat je precies invoert dan kan het inderdaad gemakkelijk gebeuren dat WolframAlpha de syntaxis niet begrijpt of verkeerd interpreteert.
Boh, site is down. Het zijn nog best leuke problemen, ik heb er van de problemen van 2000 redelijk wat gemaakt, maar ik weet niet hoeveel ik er goed hebquote:
[...]
Oh, laat maar. Ik ben net deze site tegengekomen. De makkelijkste daarvan zijn denk ik wel een goede uitdaging
Voor mijn PWS op de havo was ik maar 8 uurtjes bezig. Op de vwo was het een ander verhaal.quote:
Mensen die beweren er 1 dag aan gewerkt te hebben zijn van die nerdjes die stiekem al 2 jaar bezig zijn met voorbereiden.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
Fervent tegenstander van het korps lasergamers.
Je hebt het denk ik over het interval (0, pi/2]. Ik weet niet of ze dit pikken. Wat namelijk nog wel een beetje sneaky is, is dat in het punt 0 de afgeleides hetzelfde zijn. Dus misschien is er nog een punt x>0 ("heeeel dicht bij 0") zodat sin(x)=x. Dat mag niet, want je moet strikte ongelijkheid aantonen. Daar zou je dan nog wat voor moeten bedenken... als je het echt netjes wil doen.quote:
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
Voor welke vak is dit? Je moet overigens aantonen dat de afgeleide op het interval (0,pi/2] strikt kleiner is dan één. Dan is het goed. Je kunt het netjes maken met Riemann integratie of met de limietdefinitie van afgeleiden, de tweede is makkelijker.quote:
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening. Als ik kan aantonen dat d(sin(x))/dx op het interval (0,1] nooit groter is dan 1 is dit toch gelukt? Immers, x stijgt constant met een richtingscoëfficient van 1.
dus:
d(sin(x))/dx = cos(x)
cos(x) = 1
x = 0 ^ x = 2π
Zouden ze dit op een tentamen pikken?
[ Bericht 2% gewijzigd door Mathemaat op 23-07-2013 00:30:36 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Het punt 0 heeft niets van doen met de hele vraag, daar het punt 0 buiten het gevraagde interval valt.quote:
[..]
Je hebt het denk ik over het interval (0, pi/2]. Ik weet niet of ze dit pikken. Wat namelijk nog wel een beetje sneaky is, is dat in het punt 0 de afgeleides hetzelfde zijn. Dus misschien is er nog een punt x>0 ("heeeel dicht bij 0") zodat sin(x)=x. Dat mag niet, want je moet strikte ongelijkheid aantonen. Daar zou je dan nog wat voor moeten bedenken... als je het echt netjes wil doen.
http://fooplot.com/plot/oqbbqj2gop
Hier kun je zien wat ik bedoel. Ik zeg dat voor iedere x > 1 het evident is dat sin(x) < x, want sin(x) heeft een maximum van 1.
Dus als aan kan tonen dat op het interval (0, 1] geldt dat sin(x) nooit meer toeneemt dan y = x (met rc = 1 ), dan heb ik toch aangetoond dat sin(x) < x voor x (0, 1]? Immers, sin(x) = x voor x = 0 want dan sin(x) = 0.
y = x neemt constant toe. Als ik aantoon dat sin(x) nooit meer toeneemt op het interval (0,1] dan y = x ben ik toch klaar?quote:Dus misschien is er nog een punt x>0 ("heeeel dicht bij 0") zodat sin(x)=x. Dat mag niet, want je moet strikte ongelijkheid aantonen.
[ Bericht 7% gewijzigd door Amoeba op 23-07-2013 00:52:13 ]
Fervent tegenstander van het korps lasergamers.
Weet ik veel, calculus ofzo. Ik had ergens een vel met wat vragen gevonden en was uit pure verveling maar begonnen met het oplossen van de vragen.quote:
[..]
Voor welke vak is dit? Je moet overigens aantonen dat de afgeleide op het interval (0,pi/2] strikt kleiner is dan één. Dan is het goed. Je kunt het netjes maken met Riemann integratie of met de limietdefinitie van afgeleiden, de tweede is makkelijker.
http://www.win.tue.nl/~fransm/onderwijs/2DL00/Inhoud.pdf
Fervent tegenstander van het korps lasergamers.
Ik begrijp je wel, maar jij begrijpt mij niet. En het feit dat je er zelf nog je vraagtekens bij zet, suggereert al dat het niet een 100% rigoreus bewijs is. Aangezien calculus vaak niet 100% rigoreus is zal het daar wel voldoen. Bij een analysevak krijg je er geen punten voor.quote:
[..]
Het punt 0 heeft niets van doen met de hele vraag, daar het punt 0 buiten het gevraagde interval valt.
http://fooplot.com/plot/oqbbqj2gop
Hier kun je zien wat ik bedoel. Ik zeg dat voor iedere x > 1 het evident is dat sin(x) < x, want sin(x) heeft een maximum van 1.
Dus als aan kan tonen dat op het interval (0, 1] geldt dat sin(x) nooit meer toeneemt dan y = x (met rc = 1 ), dan heb ik toch aangetoond dat sin(x) < x voor x (0, 1]? Immers, sin(x) = x voor x = 0 want dan sin(x) = 0.
[..]
y = x neemt constant toe. Als ik aantoon dat sin(x) nooit meer toeneemt op het interval (0,1] dan y = x ben ik toch klaar?
Daarom post ik het ook hier. Verder dan dit kom ik met het vwo niet, althans, niet met het gebruik van de differentiaalrekening.quote:
[..]
Ik begrijp je wel, maar jij begrijpt mij niet. En het feit dat je er zelf nog je vraagtekens bij zet, suggereert al dat het niet een 100% rigoreus bewijs is. Aangezien calculus vaak niet 100% rigoreus is zal het daar wel voldoen. Bij een analysevak krijg je er geen punten voor.
Zou je me het ontbrekende deel uit kunnen leggen?
Fervent tegenstander van het korps lasergamers.
Bij de analysevakken krijg je netjes geleerd hoe netjes dingen op moet schrijven. Dat kun je niet even uitleggen.quote:
[..]
Daarom post ik het ook hier. Verder dan dit kom ik met het vwo niet, althans, niet met het gebruik van de differentiaalrekening.
Zou je me het ontbrekende deel uit kunnen leggen?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Oké.quote:
[..]
Bij de analysevakken krijg je netjes geleerd hoe netjes dingen op moet schrijven. Dat kun je niet even uitleggen.
Had je nog naar m'n profielwerkstuk gekeken?
Fervent tegenstander van het korps lasergamers.
Ja, het zag er idd interessant uit. Maar ik heb niet zoveel verstand van profielwerkstukken, dus ik kan er niet zoveel over zeggen .quote:
[..]
Oké.
Had je nog naar m'n profielwerkstuk gekeken?
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Waarschijnlijk is het gezien de hint de bedoeling dat je gebruik maakt van de middelwaardestelling. Deze zegt dat als een functie f: [a,b] → R continu is op [a,b] en differentieerbaar op (a,b), dat er dan een c ∈ (a,b) bestaat zodanig datquote:
Opgave 4
Laat zien dat voor alle x > 0 geldt dat sin(x) < x.
Hint: sin(x) = sin(x) - sin(0)
sin(x) heeft een maximum van 1 (voor x = 1/2 π)
Dus als ik aan kan tonen dat x > sin(x) voor x (0,1] dan heb ik in feite de opgave aangetoond. Nu wil ik dit aantonen dmv de differentiaalrekening.
f(b) − f(a) = (b − a)·f'(c).
Aangezien d(sin(x))/dx = cos(x) en 0 < cos(x) < 1 voor 0 < x < π/2 volgt dan direct sin(x) − sin(0) < (x − 0) ofwel sin(x) < x voor 0 < x < π/2, en aangezien π/2 > 1 ben je dan klaar.
Echter, om analytisch aan te tonen dat d(sin(x))/dx = cos(x) moet je gebruik maken van limθ→0 sin(θ)/θ = 1. Maar om deze limiet aan te tonen moet je eerst aantonen dat sin(θ) < θ < tan(θ) voor 0 < θ < π/2 waaruit weer volgt dat cos(θ) < sin(θ)/θ < 1 voor 0 < | θ | < π/2 zodat met behulp van de insluitstelling én de continuïteit van de cosinusfunctie in θ = 0 volgt dat limθ→0 sin(θ)/θ = 1. Als de goniometrische functies meetkundig zijn gedefinieerd aan de hand van de eenheidscirkel, dan ontkom je niet aan een meetkundige beschouwing om aan te tonen dat sin(θ) < θ < tan(θ) voor 0 < θ < π/2, zodat je in een cirkelredenatie vervalt (no pun intended) als je dan d(sin(x))/dx = cos(x) weer gaat gebruiken om met behulp van de middelwaardestelling aan te tonen dat sin(x) < x voor x > 0.
Ik heb er iets van geprobeerd te breien zonder de definitie van limieten of Rieman integralen te gebruiken.quote:
[..]
Daarom post ik het ook hier. Verder dan dit kom ik met het vwo niet, althans, niet met het gebruik van de differentiaalrekening.
Zou je me het ontbrekende deel uit kunnen leggen?
We willen aantonen dat sin(x)<x op (0, pi/2]. Oftewel x-sin(x)>0. Definieer f(x)=x-sin(x). We willen dus laten zien dat f(x)>0 voor x in (0,pi/2].
Merk op dat f(0)=0 en voor x in (0, pi/2] geldt f'(x)>0 . Voor x in (0,pi] geldt dus
De laatste stap volgt uit het feit dat f' continu is, en daarom de extreme value theorem gebruikt mag worden (http://en.wikipedia.org/wiki/Extreme_value_theorem). (Denk daar eens goed over na
)
De MAA site is niet down, maar helaas is deze site enkele dagen geleden zo maar zonder aankondiging gereorganiseerd, waardoor de oude URLs niet meer werken. En stom genoeg heeft men niet voorzien in redirects van de oude naar de nieuwe URLs, zodat veel 'oude' interne links nu ook niet meer werken. Hierdoor is het lastig materiaal terug te vinden. Ik kan de Putnam opgaven en uitwerkingen momenteel dan ook niet terugvinden, maar gelukkig hebben we voor dit soort eventualiteiten nog archive.org:quote:
[..]
Boh, site is down. Het zijn nog best leuke problemen, ik heb er van de problemen van 2000 redelijk wat gemaakt, maar ik weet niet hoeveel ik er goed heb
http://web.archive.org/we(...)ms/putnamindex.shtml
Je had beter meteen even de bron van je opgave kunnen geven. Hieruit blijkt inderdaad dat het de bedoeling is dat je gebruik maakt van de middelwaardestelling.quote:
[..]
Ik had ergens een vel met wat vragen gevonden en was uit pure verveling maar begonnen met het oplossen van de vragen.
http://www.win.tue.nl/~fransm/onderwijs/2DL00/Inhoud.pdf
Als je je verveelt en nog wat uitdagingen zoekt heb ik er nog wel eentje voor je. De afgelopen tijd heb ik vrij vaak gewezen op het belang van het kennen van merkwaardige producten en het beheersen van technieken als ontbinden in factoren en kwadraatafsplitsen in verband met het oplossen van vierkantsvergelijkingen. Deze technieken zijn natuurlijk gesneden koek voor iedereen die een beetje schoolalgebra kent, en de volgende opgaven zouden dan ook een eitje moeten zijn. Of toch niet?
Opgave 1. Ontbind a6 + b6 zo ver mogelijk in veeltermen in a en b met uitsluitend reële coëfficiënten.
Opgave 2. Idem voor a5 + b5.
Deze opgaven zijn oplosbaar met elementaire algebraïsche methoden, maar WolframAlpha en Google zullen je niet helpen (anders zou de aardigheid er snel af zijn) dus laat je kunsten maar eens zien ...
Nee natuurlijk niet, jou kennende zit ik weer tot middernacht te piekeren hoe ik dit op ga lossen.quote:
[..]
Je had beter meteen even de bron van je opgave kunnen geven. Hieruit blijkt inderdaad dat het de bedoeling is dat je gebruik maakt van de middelwaardestelling.
Als je je verveelt en nog wat uitdagingen zoekt heb ik er nog wel eentje voor je. De afgelopen tijd heb ik vrij vaak gewezen op het belang van het kennen van merkwaardige producten en het beheersen van technieken als ontbinden in factoren en kwadraatafsplitsen in verband met het oplossen van vierkantsvergelijkingen. Deze technieken zijn natuurlijk gesneden koek voor iedereen die een beetje schoolalgebra kent, en de volgende opgaven zouden dan ook een eitje moeten zijn. Of toch niet?
Opgave 1. Ontbind a6 + b6 zo ver mogelijk in veeltermen in a en b met uitsluitend reële coëfficiënten.
Opgave 2. Idem voor a5 + b5.
Deze opgaven zijn oplosbaar met elementaire algebraïsche methoden, maar WolframAlpha en Google zullen je niet helpen (anders zou de aardigheid er snel af zijn) dus laat je kunsten maar eens zien ...
Ik heb inderdaad gezien dat het onderwerp van de dag tot een paar dagen geleden ontbinden in factoren was, maar toen heb ik er niet veel aandacht aan besteed. Tijd om wat materiaal op te rakelen dus. Ik heb namelijk nog geen idee hoe ik dit aan moet pakken.
Fervent tegenstander van het korps lasergamers.
Je bent een heldquote:
[..]
De MAA site is niet down, maar helaas is deze site enkele dagen geleden zo maar zonder aankondiging gereorganiseerd, waardoor de oude URLs niet meer werken. En stom genoeg heeft men niet voorzien in redirects van de oude naar de nieuwe URLs, zodat veel 'oude' interne links nu ook niet meer werken. Hierdoor is het lastig materiaal terug te vinden. Ik kan de Putnam opgaven en uitwerkingen momenteel dan ook niet terugvinden, maar gelukkig hebben we voor dit soort eventualiteiten nog archive.org:
http://web.archive.org/we(...)ms/putnamindex.shtml
! Volgens mij hebben ze op de nieuwe/gereorganiseerde site de oude opgaven er (nog?) niet opstaan.Ik had al eens gekeken op de 'wayback machine', toen kon ik het niet vinden. Ik zal wel niet goed gekeken hebben
Ik zat laatst eens na te denken over mijn fiets (mountainbike). Ik zit te denken om andere velgen te kopen, maar ik twijfel hoeveel effect dat heeft. Het voordeel is vooral afhankelijk van de velgsnelheid.
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie beschrijft tijdens het rijden
Maar wat is dan de snelheid van dat punt? (de afgeleide/snelheid van normale sinus is cos..) Dus ik vroeg me af of een (absolute) cosinus ook de snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
[ Bericht 7% gewijzigd door the85mc op 23-07-2013 13:11:33 ]
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie beschrijft tijdens het rijden
Maar wat is dan de snelheid van dat punt? (de afgeleide/snelheid van normale sinus is cos..) Dus ik vroeg me af of een (absolute) cosinus ook de snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
[ Bericht 7% gewijzigd door the85mc op 23-07-2013 13:11:33 ]
Per meter die je band rolt ga je toch gewoon 1 meter vooruit? Dus je snelheid en die van de band moeten gelijk zijn.quote:
Ik zat laatst eens na te denken over mijn fiets (mountainbike). Ik zit te denken om andere velgen te kopen, maar ik twijfel hoeveel effect dat heeft. Het voordeel is vooral afhankelijk van de velgsnelheid.
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie maakt.
Maar wat is dan de snelheid, (de afgeleide van normale sinus is cos..) Dus ik vroeg me af of een cosinus ook de.snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
Een sinosoïde geeft slechts de "hoogte" van een punt op je band na verloop van tijd. De afgeleide daarvan is dus de component van de snelheid in de y-richting, van een bepaald punt op de band.
De as rolt inderdaad 1 meter vooruit. Masr de velg beschrijft dus een sinus functie. Dan zou je zeggen dat de snelheid tov de lucht (dus niet de weg) niet constant is.quote:
[..]
Per meter die je band rolt ga je toch gewoon 1 meter vooruit? Dus je snelheid en die van de band moeten gelijk zijn.
De angularvelocity is overal in je velg hetzelfde.quote:
Ik zat laatst eens na te denken over mijn fiets (mountainbike). Ik zit te denken om andere velgen te kopen, maar ik twijfel hoeveel effect dat heeft. Het voordeel is vooral afhankelijk van de velgsnelheid.
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie beschrijft tijdens het rijden
Maar wat is dan de snelheid van dat punt? (de afgeleide/snelheid van normale sinus is cos..) Dus ik vroeg me af of een (absolute) cosinus ook de snelheid beschrift van een absolute sinusfunctie. En wat de velgsnelheid is tov van de rijsnelheid.
Ik hoop dat mijn verhaal duidelijk is en dat iemand mij dit toe kan lichten.
Edit, mijn boerenverstand zegt dat het punt bovenaan 2x de rijsnelheid heeft, maar ik kan dit niet theoretisch bewijzen.
Afhankelijk van de afstand tot het midden is er een bepaalde snelheid im een punt.
Het punt boven of beneden heeft dezelfde snelheid. Waarom zou bovenin de snelheid 2 keer zo groot zijn?
Jawel. Stel dat je een punt markeert op je band en dat de straal 1 (meter) is. Laten we zeggen dat we de rechterkant van de band ter hoogte van de as markeren. Als de band dan naar links gaat rijden, dan volgt de hoogte van het punt op de band (ten opzichte van de as) een sinusgrafiek. De zijwaartse afwijking kan je beschrijven met een cosinus (een afwijking naar rechts kiezen we als positief).quote:
[..]
De as rolt inderdaad 1 meter vooruit. Masr de velg beschrijft dus een sinus functie. Dan zou je zeggen dat de snelheid tov de lucht (dus niet de weg) niet constant is.
De snelheid van het punt op je band is nu de vector die wordt opgespannen door de x en y component. Met de stelling van Pythagoras krijg je dan dat de lengte van deze somvector gelijk is aan cos²(t) + sin²(t) = 1. De grootte snelheid is dus constant (maar de richting verandert uiteraard).
Maar dit kan je natuurlijk ook op je klompen al aanvoelen. Als een stuk van je velg sneller zou gaan dan een ander stuk, schuift het dan in elkaar?
Ja het klopt dat rad/s constant is bij constante snelheid. Maar wat is dan de snelheid tov de x as? Die is niet constant.
Dat kan namelijk niet: de as beweegt met constante snelheid over de x as. 1 punt op de velg is het ene moment achter de as en later voor de as. Dan moet ie ergens sneller gaan dan de as snelheid.
Dat kan namelijk niet: de as beweegt met constante snelheid over de x as. 1 punt op de velg is het ene moment achter de as en later voor de as. Dan moet ie ergens sneller gaan dan de as snelheid.
Ter verduidelijking, het gaat niet om hoeksnelheid, maar snelheid tov de x as.
Wat we eigenlijk nodig hebben is een fiets en een stroboscoop
Wat we eigenlijk nodig hebben is een fiets en een stroboscoop
Oh zo.quote:
Ter verduidelijking, het gaat niet om hoeksnelheid, maar snelheid tov de x as.
Wat we eigenlijk nodig hebben is een fiets en een stroboscoop
Nou schrijf eerst eens de beweging op in referenceframe van middelpunt wiel en dan vanuit de weg.
Moet nit zo moeilik zijn toch?
Hier ga je al de fout in. Een punt op de velg beschrijft tijdens het rijden over een vlakke weg een cycloïde. Als je even de moeite neemt het Wikipedia artikel door te nemen krijg je antwoord op je vragen. Ik begrijp trouwens niet wat je hier nu precies mee wil. Als je uitgaat van de parametervoorstelling die in het artikel wordt gegeven, dan kun je x'(t) en y'(t) berekenen en daarmee dus ook de grootte van de snelheid v(t) = √(((x'(t))2 + (y'(t))2) van een punt op de velg op elk tijdstip t.quote:
Ik zat laatst eens na te denken over mijn fiets (mountainbike). Ik zit te denken om andere velgen te kopen, maar ik twijfel hoeveel effect dat heeft. Het voordeel is vooral afhankelijk van de velgsnelheid.
Als je naar 1 punt op de velg kijkt dan zie je dat dat punt een absolute sinus functie beschrijft tijdens het rijden
Maar wat is dan de snelheid van dat punt?
mag je *-1 doen?quote:
[..]
Opgave 1. Ontbind a6 + b6 zo ver mogelijk in veeltermen in a en b met uitsluitend reële coëfficiënten.
Opgave 2. Idem voor a5 + b5.
Overigens zijn die parametervoorstellingen niet eens zo moeilijk aan te tonen. Ik heb dat ook ooit moeten doen bij wiskunde D.quote:
[..]
Hier ga je al de fout in. Een punt op de velg beschrijft tijdens het rijden over een vlakke weg een cycloïde. Als je even de moeite neemt het Wikipedia artikel door te nemen krijg je antwoord op je vragen. Ik begrijp trouwens niet wat je hier nu precies mee wil. Als je uitgaat van de parametervoorstelling die in het artikel wordt gegeven, dan kun je x'(t) en y'(t) berekenen en daarmee dus ook de grootte van de snelheid v(t) = √(((x'(t))2 + (y'(t))2) van een punt op de velg op elk tijdstip t.
Fervent tegenstander van het korps lasergamers.
(a*a2)(a*a2)+(b*b2)(b*b2)quote:
[..]
Nee, het is niet de bedoeling de opgave te veranderen in iets anders.
Dat is triviaal, en niet de bedoeling. Een uitdrukking als a6 + b6 ontbinden wil zeggen dat je de gegeven uitdrukking herschrijft als een product van een aantal factoren die elk veeltermen zijn in a en b. Elk van deze veeltermen in a en b mag uitsluitend reële coëfficiënten hebben en geen van deze veeltermen mag nog verder zijn te ontbinden.quote:
Opgave 1: (a6 + b6) = (a3 + b3)(a3 - b3) = (a+b)(a2 - ab + b2)(a-b)(a2 + ab + b2)quote:
[..]
Opgave 1. Ontbind a6 + b6 zo ver mogelijk in veeltermen in a en b met uitsluitend reële coëfficiënten.
Opgave 2. Idem voor a5 + b5.
Bedoel je dit?
huh er staat +quote:
[..]
Opgave 1: (a6 + b6) = (a3 + b3)(a3 - b3) = (a+b)(a2 - ab + b2)(a-b)(a2 + ab + b2)
Bedoel je dit?
Je begrijpt in ieder geval wat de bedoeling is, maar dit is niet goed, want (a3 + b3)(a3 − b3) = a6 − b6.quote:
[..]
Opgave 1: (a6 + b6) = (a3 + b3)(a3 - b3) = (a+b)(a2 - ab + b2)(a-b)(a2 + ab + b2)
Bedoel je dit?
quote:
[..]
Je begrijpt in ieder geval wat de bedoeling is, maar dit is niet goed, want (a3 + b3)(a3 − b3) = a6 − b6.
dacht dat ik a6 − b6 moest ontbinden. Ik heb geen idee hoe je a6 + b6 moet ontbinden en de 2e opgave lijkt me nog lastiger aangezien het een oneven macht is. Zou je me misschien op weg kunnen helpen? (wellicht via een DM om de andere niet te spoilen)
Tuurlijk zou ik hints kunnen geven via DM, maar dan heb je een voorsprong t.o.v. anderen die het wellicht ook willen proberen, en dat is niet fair. En met hints geven op het forum is de aardigheid er ook snel af. Ik vind het gewoon leuk om te zien waar mensen allemaal mee aan komen zetten. Misschien bedenkt iemand wel een elegante herleiding die ik zelf nog niet had bedacht. Ik denk inderdaad ook dat de tweede opgave lastiger is.quote:Op dinsdag 23 juli 2013 15:39 schreef spacer730 het volgende:
[..]
Dat had ik ook al bedacht. Ik heb uiteraard even op WolframAlpha gespiekt, daar staat natuurlijk het antwoord, maar niet de herleiding. Zodoende moet het hier wel op lijken..quote:
[..]
Je begrijpt in ieder geval wat de bedoeling is, maar dit is niet goed, want (a3 + b3)(a3 − b3) = a6 − b6.
Als je gebruikt dat a^6 + b^6 = 0
Dan geldt ook dat:
a^6 - b^6 = -2b^6
Of mag ik niet stellen dat a^6 + b^6 = 0?
Overigens geen idee of dit de goede weg is.. Ik probeer ook maar wat.
Fervent tegenstander van het korps lasergamers.
Moet je het als a^6-a^6 uitrekenen, maar dan aan rechterkant telkens aanvullen tot +a^6?quote:
[..]
Je begrijpt in ieder geval wat de bedoeling is, maar dit is niet goed, want (a3 + b3)(a3 − b3) = a6 − b6.
Nee, dat mag niet. Je moet het schrijven als een product. Dus (...)(....) = a^6 + b^6quote:
[..]
Moet je het als a^6-a^6 uitrekenen, maar dan aan rechterkant telkens aanvullen tot +a^6?
Kijk eens hier
Fervent tegenstander van het korps lasergamers.
De truc hier is om je probleem voor een specifiek geval op te lossen en dat algemener te maken.quote:
[..]
Nee natuurlijk niet, jou kennende zit ik weer tot middernacht te piekeren hoe ik dit op ga lossen.
Ik heb inderdaad gezien dat het onderwerp van de dag tot een paar dagen geleden ontbinden in factoren was, maar toen heb ik er niet veel aandacht aan besteed. Tijd om wat materiaal op te rakelen dus. Ik heb namelijk nog geen idee hoe ik dit aan moet pakken.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
(a+b)(a^2 - ab + b^2)(a-b)(a^2 + ab + b^2)+2b^6quote:
[..]
Nee, dat mag niet. Je moet het schrijven als een product. Dus (...)(....) = a^6 + b^6
Kijk eens hier
Hoe zet je 2b^6 in haakjes?
Ik denk niet dat dit de goede manier is. Ieder product bevat a, dus wordt het lastig om a te elimineren.quote:
[..]
(a+b)(a^2 - ab + b^2)(a-b)(a^2 + ab + b^2)+2b^6
Hoe zet je 2b^6 in haakjes?
Fervent tegenstander van het korps lasergamers.
Niet echt. Het antwoord dat WolframAlpha geeft voldoet niet aan de opdracht om a6 + b6 zo ver mogelijk te ontbinden in tweetermen in a en b met reële coëfficiënten.quote:
[..]
Dat had ik ook al bedacht. Ik heb uiteraard even op WolframAlpha gespiekt, daar staat natuurlijk het antwoord, maar niet de herleiding.
is dit een tussenstap?quote:
[..]
Niet echt. Het antwoord dat WolframAlpha geeft voldoet niet aan de opdracht om a6 + b6 zo ver mogelijk te ontbinden in tweetermen in a en b met reële coëfficiënten.
(a2*a4)+((ab*(ab)2)-(ab*(ab)2))+(b2*b4)
of:
a6 +a3b3 -(a3b3)+b6
(a6 +a3b3) -((a3b3)+b6)
a3(a3 +b3) -b3(a3 +b3)
(a3 -b3) (a3 +b3)2
(a-b) (a2+a b+b2)(a6+2a3 b3+b6)
[ Bericht 4% gewijzigd door wiskundenoob op 23-07-2013 21:12:41 ]
Kijk eens naar je laatste regel.Er staat nog steeds a^6 + b^6 in je laatste product. Dan ben je toch niets opgeschoten?
Daarnaast is het allemaal vergeefse moeite
[ Bericht 48% gewijzigd door Amoeba op 23-07-2013 21:36:10 ]
Daarnaast is het allemaal vergeefse moeite
[ Bericht 48% gewijzigd door Amoeba op 23-07-2013 21:36:10 ]
Fervent tegenstander van het korps lasergamers.
Als je iets ontbindt, moet je het in verschillende factoren zetten (in de uitdrukking a * b zijn a en b factoren).quote:
Jij zet het antwoord in termen (in de uitdrukking a + b zijn a en b termen).
Je begrijpt het al, wiskundenoob?
Riparius, ik heb ooit eens wat regels geleerd voor het ontbinden van dat soort expressies in factoren. Ik ben het een keer in een boek (een boek dat overigens bekend is geworden doordat het een bron van informatie voor Ramanujan, een bijzondere en grote wiskundige die inmiddels is overleden, was. Dit is overigens ook de reden dat ik er eens een kijkje in heb genomen: er staat inderdaad veel nuttigs in, maar het is niet erg leesbaar) tegengekomen, en ik heb het een keer tijdens getaltheorie nodig gehad (als ik het me goed herinner, ik begin nu een beetje te twijfelen).
Ik kom zover:
(a3 + b3) = (a + b)(a2 + b2 - ab)
Als ipv a en b a2 en b2 gebruikt kan je inderdaad de expressie van Riparius ontbinden. (maar ik zie nu dat Amoeba ook al zover was gekomen, met behulp van wolfram alpha). Hoewel de rechterkant nu precies in een kwadratische vorm staat (na de substitutie x=a is dit middschien duidelijker: x2-bx+b2), heeft deze vergelijking geen oplossingen
Helaas is dit een onderwerp waar ik niet veel kaas van gegeten heb. Ik heb al een paar keer bedacht dat ik er eigenlijk wat meer moeite aan zou moeten besteden, en ik heb dat ook een keer gedaan, maar ik kon niet echt dingen op internet vinden (mede doordat ik niet goed wist waar ik naar moest zoeken: ik vond vooral pagina's die de abc-formule uitlegden).
Ik dacht net even dat ik hem had, maar toen had ik (a2 + b2 + ab) ontbonden ipv (a2 + b2 - ab)...
[ Bericht 6% gewijzigd door randomo op 23-07-2013 23:48:40 ]
Riparius, ik heb ooit eens wat regels geleerd voor het ontbinden van dat soort expressies in factoren. Ik ben het een keer in een boek (een boek dat overigens bekend is geworden doordat het een bron van informatie voor Ramanujan, een bijzondere en grote wiskundige die inmiddels is overleden, was. Dit is overigens ook de reden dat ik er eens een kijkje in heb genomen: er staat inderdaad veel nuttigs in, maar het is niet erg leesbaar) tegengekomen, en ik heb het een keer tijdens getaltheorie nodig gehad (als ik het me goed herinner, ik begin nu een beetje te twijfelen).
Ik kom zover:
(a3 + b3) = (a + b)(a2 + b2 - ab)
Als ipv a en b a2 en b2 gebruikt kan je inderdaad de expressie van Riparius ontbinden. (maar ik zie nu dat Amoeba ook al zover was gekomen, met behulp van wolfram alpha). Hoewel de rechterkant nu precies in een kwadratische vorm staat (na de substitutie x=a is dit middschien duidelijker: x2-bx+b2), heeft deze vergelijking geen oplossingen
Helaas is dit een onderwerp waar ik niet veel kaas van gegeten heb. Ik heb al een paar keer bedacht dat ik er eigenlijk wat meer moeite aan zou moeten besteden, en ik heb dat ook een keer gedaan, maar ik kon niet echt dingen op internet vinden (mede doordat ik niet goed wist waar ik naar moest zoeken: ik vond vooral pagina's die de abc-formule uitlegden).
Ik dacht net even dat ik hem had, maar toen had ik (a2 + b2 + ab) ontbonden ipv (a2 + b2 - ab)...
[ Bericht 6% gewijzigd door randomo op 23-07-2013 23:48:40 ]
Hier maak je al een tekenfout: − (a3b3) + b6 = − ((a3b3) − b6).quote:
[..]
a6 + a3b3 - (a3b3) + b6
(a6 + a3b3) - ((a3b3) + b6)
Dat is uiteraard een correcte observatie. Als we in het merkwaardig productquote:
Ik kom zover:
(a3 + b3) = (a + b)(a2 + b2 - ab)
Als i.p.v. a en b a2 en b2 gebruikt kan je inderdaad de expressie van Riparius ontbinden (maar ik zie nu dat Amoeba ook al zover was gekomen, met behulp van WolframAlpha).
(a + b)(a2 − ab + b2) = a3 + b3
a2 in de plaats stellen van a en b2 in de plaats van b, dan hebben we
a6 + b6 = (a2 + b2)(a4 − a2b2 + b4)
en dat is wat WolframAlpha ook geeft.
Dat is ook een goede observatie: a2 − ab + b2 is inderdaad irreducibel over R, en dat kun je gemakkelijk zien door deze veelterm op te vatten als een kwadratisch polynoom in één variabele. Nemen we a als variabele dan is de discriminant −3b2 en dus negatief voor elke reële b ≠ 0, zodat dit polynoom voor b ≠ 0 niet is te schrijven als een product van twee lineaire factoren met reële coëfficiënten. Aangezien het polynoom symmetrisch is in a en b geldt uiteraard mutatis mutandis hetzelfde als we omgekeerd b opvatten als variabele en a als constante. Het feit dat a2 − ab + b2 irreducibel is over R impliceert echter niet dat a4 − a2b2 + b4 ook irreducibel zou zijn over R, en dat is dan ook niet zo.quote:Hoewel de rechterkant nu precies in een kwadratische vorm staat (na de substitutie x=a is dit misschien duidelijker: x2-bx+b2), heeft deze vergelijking geen oplossingen.
Ik ken de merkwaardige producten voor polynomen van de derde graad helemaal niet. Misschien was dat het probleem zodat ik geen idee had waar te beginnen.quote:
[..]
Dat is uiteraard een correcte observatie. Als we in het merkwaardig product
(a + b)(a2 − ab + b2) = a3 + b3
a2 in de plaats stellen van a en b2 in de plaats van b, dan hebben we
a6 + b6 = (a2 + b2)(a4 − a2b2 + b4)
en dat is wat WolframAlpha ook geeft.
[..]
Dat is ook een goede observatie: a2 − ab + b2 is inderdaad irreducibel over R, en dat kun je gemakkelijk zien door deze veelterm op te vatten als een kwadratisch polynoom in één variabele. Nemen we a als variabele dan is de discriminant −3b2 en dus negatief voor elke reële b ≠ 0, zodat dit polynoom voor b ≠ 0 niet is te schrijven als een product van twee lineaire factoren met reële coëfficiënten. Aangezien het polynoom symmetrisch is in a en b geldt uiteraard mutatis mutandis hetzelfde als we omgekeerd b opvatten als variabele en a als constante. Het feit dat a2 − ab + b2 irreducibel is over R impliceert echter niet dat a4 − a2b2 + b4 ook irreducibel zou zijn over R, en dat is dan ook niet zo.
Maar je meent nu te zeggen dat het mogelijk is om a4 -a2b2 + b4 te schrijven is, zoals jij dat zo mooi weet te zeggen, als een product van twee lineaire factoren met reële coëfficiënten.
Dat lijkt me nog een aardige uitdaging.
Fervent tegenstander van het korps lasergamers.
Ik had de term merkwaardige producten al genoemd bij de opgave, bedoeld als hint, en dan kan het natuurlijk geen kwaad even het Wikipedia artikel hierover door te kijken.quote:
[..]
Ik ken de merkwaardige producten voor polynomen van de derde graad helemaal niet. Misschien was dat het probleem zodat ik geen idee had waar te beginnen.
Nou nee, dit is niet wat ik hierboven zeg. De veelterm a4 − a2b2 + b4 is niet te schrijven als een product van (vier, niet twee) lineaire veeltermen in a en b met reële coëfficiënten. Maar deze veelterm is wél reducibel over R, dus je kunt dit nog verder ontbinden in veeltermen in a en b met reële coëfficiënten. Maar hoe?quote:Maar je meent nu te zeggen dat het mogelijk is om a4 - a2b2 + b4 te schrijven is, zoals jij dat zo mooi weet te zeggen, als een product van twee lineaire factoren met reële coëfficiënten.
Dat lijkt me nog een aardige uitdaging.
Ja, maar dat is een tautologie, lineaire veeltermen zijn per definitie eerstegraads veeltermen. Maar zoals gezegd is a4 − a2b2 + b4 niet te ontbinden in lineaire veeltermen in a en b met reële coëfficiënten, wel op een andere manier.quote:
[..]
Even kijken of ik dit goed begrepen heb.
Als het te schrijven is als 4 lineaire veeltermen in a en b met reële coëfficiënten dan geldt dat iedere factor van ten hoogste graad 1 is?
Krijg je het juiste antwoord als ik dit uitwerk?quote:
[..]
Hier maak je al een tekenfout: − (a3b3) + b6 = − ((a3b3) − b6).
[ Bericht 0% gewijzigd door wiskundenoob op 24-07-2013 17:51:29 ]
Het is nu nog een kwestie van het ontbinden van a4 -(ab)2 + b4 in factoren. Zoals Randomo al terecht opmerkte maak jij er een puinhoop met termen van.quote:
[..]
Krijg je het juiste antwoord als ik dit uitwerkt?
Fervent tegenstander van het korps lasergamers.
Pfff het zijn gewoon factoren....quote:
[..]
Het is nu nog een kwestie van het ontbinden van a4 -(ab)2 + b4 in factoren. Zoals Randomo al terecht opmerkte maak jij er een puinhoop met termen van.
[ Bericht 2% gewijzigd door wiskundenoob op 24-07-2013 18:15:23 ]
a is een term, b is een term, (a+b) is hier een factorquote:
[..]
Is (a+b)(a+b) nou een term of een factor?..
quote:
[..]
Pfff het zijn gewoon factoren....
Luister nou maar naar wat vader Thenxero zegt.quote:
[..]
a is een term, b is een term, (a+b) is hier een factor
Fervent tegenstander van het korps lasergamers.
Ik vermoedde inderdaad al dat a2 - ab + b2 irreducibel is en a4 - a2b2 + b4 niet, maar helaas houdt het daar ook mee op: ik ken geen merkwaardig product dat me kan helpen, maar ik meen me te herinneren dat in het pdf'je uit mijn vorige post zulke producten systematisch uitgewerkt staan (maar dat vind ik zelf een beetje richting spieken gaan, ik wacht nog even af of ik of iemand anders misschien een 'sudden realization' heeft die ons verder kan helpen).quote:
[...]
Dat is ook een goede observatie: a2 − ab + b2 is inderdaad irreducibel over R, en dat kun je gemakkelijk zien door deze veelterm op te vatten als een kwadratisch polynoom in één variabele. Nemen we a als variabele dan is de discriminant −3b2 en dus negatief voor elke reële b ≠ 0, zodat dit polynoom voor b ≠ 0 niet is te schrijven als een product van twee lineaire factoren met reële coëfficiënten. Aangezien het polynoom symmetrisch is in a en b geldt uiteraard mutatis mutandis hetzelfde als we omgekeerd b opvatten als variabele en a als constante. Het feit dat a2 − ab + b2 irreducibel is over R impliceert echter niet dat a4 − a2b2 + b4 ook irreducibel zou zijn over R, en dat is dan ook niet zo.
Overigens, ik bedacht me net iets wat misschien goed (voor je inzicht) is om te realiseren.
Bij het ontbinden van een kwadratische vergelijking zoek je meestal naar nulpunten, en het ontbinden van een expressie als x^3+y^3 kan op soortgelijke wijze.
Als je x3 + y3 = 0 stelt, kan je al snel zien dat x = -y een oplossing is.
Dat betekent dat x + y = 0 impliceert dat x3 + y3 = 0. Oftewel, x + y is een factor van x3 + y3. Op dezelfde wijze kan je snel en makkelijk factoren van bijvoorbeeld x3 - y3 en x4 - y4 vinden. Hoewel het onthouden van merkwaardige producten sneller is, kan voor simpele polynomen ook deze manier gebruiken.
Helaas helpt dit niet veel bij het ontbinden van ingewikkeldere expressies zoals a4 - a2b2 + b4. Het enige wat ik nog kan verzinnen is om factoren te proberen en deze proberen er met een staartdeling uit te halen.
Nu kan je wel wat voorwaarden stellen aan de factoren: je weet al dat de factoren niet lineair zijn in a of b, dus factoren van de vorm (a + k * b) hoef je niet te proberen (dit heeft Riparius al verklapt, en verder kan je het inzien omdat a = -k * b geen nulpunten van de vergelijking a4 - a2b2 + b4 geeft: dit kan je controleren door in te vullen, misschien zijn er makkelijkere manieren). Dus moeten de factoren een term a2, b2 of ab hebben (en ik kan zelfs niet uitsluiten dat er termen als a2b in voorkomen). De expressie is symmetrisch in a en b, maar je kan hier niet uit concluderen dat elke factor dat ook moet zijn: (a + 5)(b + 5) = ab + 5a + 5b is bijvoorbeeld ook symmetrisch in a en b, maar zijn factoren zijn dat niet.
edit: verder weet je, omdat (zoals Riparius in zijn post hiervoor uitlegt) a2 - ab + b2 irreducibel is, dat a4 - a2b2 + b4 geen factoren van de vorm (a2 - k) heeft (dit zou namelijk impliceren dat a2 - ab + b2 wel reducibel is, namelijk met een factor (a - k)). Door de symmetrie in a en b geldt natuurlijk hetzelfde als we b in plaats van a gebruiken.
Er blijven helaas nog een heleboel mogelijke vormen over die factoren wèl kunnen hebben. Ik kom er niet uit, en zie dus waarschijnlijk iets over het hoofd (het is ooit door iemand ontbonden, en die zal vast niet blindelings factoren hebben geprobeerd)...
TLDR; het lukt me niet
[ Bericht 7% gewijzigd door randomo op 24-07-2013 23:15:39 ]
Hoe ontbind je dan makkelijk? Ik snap dat x = -y maar zie niet hoe dat helpt...quote:Op woensdag 24 juli 2013 23:16 schreef randomo het volgende:
Ja, ik heb een beetje saaie vakantie tot nu toe, vandaar mijn lange post
Als je x3 + y3 = 0 stelt, kan je al snel zien dat x = -y een oplossing is.Dat betekent dat x + y = 0 impliceert dat x3 + y3 = 0. Oftewel, x + y is een factor van x3 + y3. Op dezelfde wijze kan je snel en makkelijk factoren van bijvoorbeeld x3 - y3 en x4 - y4 vinden. Hoewel het onthouden van merkwaardige producten sneller is, kan voor simpele polynomen ook deze manier gebruiken.
x^3 - x^3 van maken? Of heb je ovetr wat anders..
Hehehe, wat een feest van herkenning; alsof ik gevraagd wordt ∫1/(x4+1) dx te integrerenquote:
Nou nee, dit is niet wat ik hierboven zeg. De veelterm a4 − a2b2 + b4 is niet te schrijven als een product van (vier, niet twee) lineaire veeltermen in a en b met reële coëfficiënten. Maar deze veelterm is wél reducibel over R, dus je kunt dit nog verder ontbinden in veeltermen in a en b met reële coëfficiënten. Maar hoe?
...Hint: Je moet hier gebruik maken van een licht gewijzigde vorm van de identiteit van Argand, nl:
(A2+√3*AB+B2)*(A2-√3*AB+B2) =
A4 +√3*A3B +A2B2 -√3*A3B -3*A2B2 -√3*AB3 +A2B2 +√3*AB3 +B4 =
A4 +√3*A3B +A2B2 -√3*A3B -3*A2B2 -√3*AB3 +A2B2 +√3*AB3 +B4 =
A4 -A2B2 +B4
De truc zit-em hierin: Je moet de middelste termen AB van een dusdanige factor extra voorzien, dat na het uitschrijven van het product (A^2 + m*A*B + B^2)(A^2 - n*A*B + B^2)
-1.) alle termen die een factor tot de macht 3 bevatten tegen elkaar wegvallen, wat de voorwaarde m = -n oplevert, en
-2.) dat de som van alle termen met A2B2 de middelste term in de te ontbinden uitdrukking oplevert. Dit geeft als voorwaarde n*m + 2 = -1
Deze voorwaarden uitwerken geeft:
nm +2 = -1
nm = -3
En omdat volgens voorwaarde 1.) geldt m = -n, krijgen we uiteindelijk
-m2 = -3
m2 = 3
m = √3 ∨ -√3 en dus ook n = √3 ∨ -√3
Hieruit volgt dat de gezochte factoren voor de middelste termen in de kwadratische polynomen zijn √3 en -√3
Vervolgens kan je met de wortelformule checken of de gevonden kwadratische polynomen nog verder te ontbinden zijn.
NB: dat de engelse Wikipedia over merkwaardige producten die Identiteit niet vermeldt is echt wel
.[ Bericht 0% gewijzigd door VanishedEntity op 25-07-2013 00:33:03 ]
Als je ziet dat x + y = 0 impliceert dat x3 + y3, weet je dat (x + y) een factor van x3 + y3 is. Veel makkelijker kan ik het niet uitleggen.quote:
[..]
Hoe ontbind je dan makkelijk? Ik snap dat x = -y maar zie niet hoe dat helpt...
x^3 - x^3 van maken? Of heb je ovetr wat anders..
[ Bericht 0% gewijzigd door randomo op 25-07-2013 00:11:46 ]
Mooi dat je het post (met uitleg, hulde!), ik denk niet dat ik er uit was gekomen.quote:
(Onbegrijpelijk trouwens, hoe mensen op sommige identiteiten komen...)
[ Bericht 7% gewijzigd door randomo op 25-07-2013 00:16:00 ]
Daarvoor is het nog x+y, maar wat heb je dan opgelost?quote:
[..]
Als je ziet dat x - y = 0 impliceert dat x3 + y3, weet je dat (x - y) een factor van x3 + y3 is. Veel makkelijker kan ik het niet uitleggen.
Je hebt gelijk, ik bedoelde x + y (ik heb het inmiddels gewijzigd). Dan heb je dus een factor van x3 + y3 gevonden.quote:
[..]
Daarvoor is het nog x+y, maar wat heb je dan opgelost?
[ Bericht 13% gewijzigd door randomo op 25-07-2013 01:06:16 ]
Ok ik denk dat ik het snap. x^3-y^3, x = y. 1 vd factor van x^3 -y^3 is (x-y) ?quote:
[..]
Je hebt gelijk, ik bedoelde x + y (ik las x = -y even als x - y = 0, for some reason, de smiley
[ Bericht 0% gewijzigd door wiskundenoob op 25-07-2013 00:29:47 ]
Jullie kunnen ook gewoon de hoofdstelling van de algebra gebruiken...
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Je schrijft het niet erg duidelijk op, maar ik geloof dat je begrijpt wat ik bedoeldequote:
[..]
Ok ik denk dat ik het snap. x^3-y^3, x = y 1 vd factor van x3 -y3 is (x-y) ?
Die gaat alleen over complexe variabelen, en geeft alleen aan dat zo'n ontbinding bestaat, niet wat deze is (en volgens mij niet eens dat deze uniek is, maar dat weet ik niet helemaal zeker).quote:
Jullie kunnen ook gewoon de hoofdstelling van de algebra gebruiken...
Echt niet? Het is echt verbluffend eenvoudig als je het ziet ...quote:
[..]
Ik vermoedde inderdaad al dat a2 - ab + b2 irreducibel is en a4 - a2b2 + b4 niet, maar helaas houdt het daar ook mee op: ik ken geen merkwaardig product dat me kan helpen,
Ik heb het boek van Carr even doorgenomen (dank trouwens om me hierop te attenderen, ik kende het niet), maar hier staat het voor zover ik zie niet in. Nu ja, indirect wel maar daar zeg ik maar even niets over.quote:maar ik meen me te herinneren dat in het pdf'je uit mijn vorige post zulke producten systematisch uitgewerkt staan (maar dat vind ik zelf een beetje richting spieken gaan, ik wacht nog even af of ik of iemand anders misschien een 'sudden realization' heeft die ons verder kan helpen).
Inderdaad, dat is zeker een bruikbare methode.quote:Overigens, ik bedacht me net iets wat misschien goed (voor je inzicht) is om te realiseren.
Bij het ontbinden van een kwadratische vergelijking zoek je meestal naar nulpunten, en het ontbinden van een expressie als x^3+y^3 kan op soortgelijke wijze.
Als je x3 + y3 = 0 stelt, kan je al snel zien dat x = -y een oplossing is.
Dat betekent dat x + y = 0 impliceert dat x3 + y3 = 0. Oftewel, x + y is een factor van x3 + y3. Op dezelfde wijze kan je snel en makkelijk factoren van bijvoorbeeld x3 - y3 en x4 - y4 vinden. Hoewel het onthouden van merkwaardige producten sneller is, kan voor simpele polynomen ook deze manier gebruiken.
Toch zou je de methode die je zelf aangeeft hier kunnen gebruiken. Ik zou het niet aanraden, maar het kan: je hebt uitsluitend even machten van a en b, dus als je bijvoorbeeld a2 = x substitueert, dan heb je x2 - b2x + b4. De discriminant van deze kwadratische veelterm in x is negatief voor b ≠ 0, zodat je dan twee toegevoegd complexe waarden voor x = a2 vindt die elk weer twee (complexe) waarden voor a uitgedrukt in b opleveren ...quote:Helaas helpt dit niet veel bij het ontbinden van ingewikkeldere expressies zoals a4 - a2b2 + b4. Het enige wat ik nog kan verzinnen is om factoren te proberen en deze proberen er met een staartdeling uit te halen.
De vergelijking k4 − k2 + 1 = 0 heeft inderdaad geen reële oplossingen dus een ontbinding in vier lineaire veeltermen in a en b met reële coëfficiënten is niet mogelijk.quote:Nu kan je wel wat voorwaarden stellen aan de factoren: je weet al dat de factoren niet lineair zijn in a of b, dus factoren van de vorm (a + k * b) hoef je niet te proberen (dit heeft Riparius al verklapt, en verder kan je het inzien omdat a = -k * b geen nulpunten van de vergelijking a4 - a2b2 + b4 geeft: dit kan je controleren door in te vullen, misschien zijn er makkelijkere manieren).
Dit is juist opgemerkt.quote:Dus moeten de factoren een term a2, b2 of ab hebben (en ik kan zelfs niet uitsluiten dat er termen als a2b in voorkomen). De expressie is symmetrisch in a en b, maar je kan hier niet uit concluderen dat elke factor dat ook moet zijn: (a + 5)(b + 5) = ab + 5a + 5b is bijvoorbeeld ook symmetrisch in a en b, maar zijn factoren zijn dat niet.
En ook dit is juist opgemerkt.quote:edit: verder weet je, omdat (zoals Riparius in zijn post hiervoor uitlegt) a2 - ab + b2 irreducibel is, dat a4 - a2b2 + b4 geen factoren van de vorm (a2 - k) heeft (dit zou namelijk impliceren dat a2 - ab + b2 wel reducibel is, namelijk met een factor (a - k)). Door de symmetrie in a en b geldt natuurlijk hetzelfde als we b in plaats van a gebruiken.
Je ziet inderdaad iets over het hoofd.quote:Er blijven helaas nog een heleboel mogelijke vormen over die factoren wèl kunnen hebben. Ik kom er niet uit, en zie dus waarschijnlijk iets over het hoofd (het is ooit door iemand ontbonden, en die zal vast niet blindelings factoren hebben geprobeerd)...
aargh!
. Ik kijk morgen nog wel even.
Ik zou het trouwens ook nog niet zien als ik de identiteit van Argand wel kende. Wat dat betreft is het een zeer geschikt probleem om mijn kennis eens bij te schaven
Ok, maar dat geldt wel voor meer dingen, vooral in de wiskundequote:
[..]
Echt niet? Het is echt verbluffend eenvoudig als je het ziet ...
. Ik kijk morgen nog wel even.Ik zou het trouwens ook nog niet zien als ik de identiteit van Argand wel kende. Wat dat betreft is het een zeer geschikt probleem om mijn kennis eens bij te schaven
Wow, Riparius, je hebt gelijk: achteraf sla ik mezelf voor mijn kop dat ik het niet zag. Je kan gewoon een soort 'completing the square' gebruiken (ik weet niet helemaal of ik die term correct gebruik, ik dacht dat het de Engelse benoeming is voor technieken als deze):
SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Er is niets onbegrijpelijks aan, en ik denk dat een beetje HBS'er of gymnasiast hier pakweg een eeuw geleden of zelfs een halve eeuw geleden geen moeite mee zou hebben gehad. Je was zelf al op het idee gekomen om in het merkwaardig productquote:
[..]
(Onbegrijpelijk trouwens, hoe mensen op sommige identiteiten komen...)
(a + b)(a2 − ab + b2) = a3 + b3
a2 in de plaats te stellen van a en b2 in de plaats van b, zodat je vond
a6 + b6 = (a2 + b2)(a4 − a2b2 + b4)
Welnu, als je in het merkwaardig product
(a + b)2 = a2 + 2ab + b2
op dezelfde manier a2 in de plaats stelt van a en b2 in de plaats van b, dan heb je
a4 + 2a2b2 + b4 = (a2 + b2)2
Het linkerlid lijkt nu erg op a4 − a2b2 + b4, nauwkeuriger gezegd, het verschil met a4 + 2a2b2 + b4 bedraagt 3a2b2. We hebben dus
a4 − a2b2 + b4 = (a2 + b2)2 − 3a2b2
Dit is in feite niets anders dan het toepassen van kwadraatafsplitsing: a4 + b4 = (a2 + b2)2 − 2a2b2. Nu willen we het rechterlid schrijven als een verschil van twee kwadraten, omdat we dan het merkwaardig product a2 − b2 = (a + b)(a − b) kunnen toepassen. We hebben 3a2b2 = (√3·ab)2, en dus hebben we
a4 − a2b2 + b4 = (a2 + b2)2 − (√3·ab)2
en dit geeft
a4 − a2b2 + b4 = ((a2 + b2) + √3·ab)((a2 + b2) − √3·ab)
oftewel
a4 − a2b2 + b4 = (a2 + √3·ab + b2)(a2 − √3·ab + b2)
zodat we uiteindelijk krijgen
a6 + b6 = (a2 + b2)(a2 + √3·ab + b2)(a2 − √3·ab + b2)
Elk van de kwadratische veeltermen in a en b in het rechterlid is irreducibel over R, zoals je gemakkelijk kunt nagaan door de discriminanten van deze veeltermen te berekenen. En uiteraard kun je deze identiteit nu controleren in WolframAlpha.
De kwadratische veeltermen in het rechterlid zijn niet irreducibel over C, dus als je wel complexe coëfficiënten toestaat, dan kun je a6 + b6 wel schrijven als het product van zes lineaire factoren in a en b, en dan krijg je dit. Deze lineaire factorisatie hangt uiteraard samen met de wortels van de vergelijking z6 = −1. Als je a/b = z substitueert, oftewel a = bz, dan heb je a6 + b6 = b6(z6 + 1) zodat het ontbinden in lineaire factoren neerkomt op het oplossen in C van de vergelijking z6 + 1 = 0. De beeldpunten in het complexe vlak van de oplossingen van deze vergelijking vormen zoals bekend een regelmatige zeshoek waarvan de hoekpunten op de eenheidscirkel liggen.
quote:
Wow, Riparius, je hebt gelijk: achteraf sla ik mezelf voor mijn kop dat ik het niet zag. Je kan gewoon een soort 'completing the square' gebruiken (ik weet niet helemaal of ik die term correct gebruik, ik dacht dat het de Engelse benoeming is voor technieken als deze):Inderdaad, dat is het. Je was me net voor omdat ik bezig was het allemaal nog eens netjes uit te leggen in de post hierboven (die natuurlijk ook voor de andere meelezers is bedoeld).SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Maar goed, nu nog de vraag hoe je
a5 + b5
zo ver mogelijk ontbindt in veeltermen in a en b met uitsluitend reële coëfficiënten. Dit is lastiger, maar je kunt dezelfde elementaire technieken gebruiken.
Goed, ook ik lees de Portugese wikipedia eens door.
Dus:
(a+b)(a4 -a3b +(ab)2 -ab3+b4) = a5 + b5
Dan rest ons het ontbinden van (a4 -a3b +(ab)2 -ab3+b4) in factoren.. Nu buig ik me weer over mijn schrift.
Ook dit zal wel weer niet mogelijk zijn in lineaire veeltermen..
[ Bericht 20% gewijzigd door Amoeba op 25-07-2013 02:08:59 ]
Dus:
(a+b)(a4 -a3b +(ab)2 -ab3+b4) = a5 + b5
Dan rest ons het ontbinden van (a4 -a3b +(ab)2 -ab3+b4) in factoren.. Nu buig ik me weer over mijn schrift.
Ook dit zal wel weer niet mogelijk zijn in lineaire veeltermen..
[ Bericht 20% gewijzigd door Amoeba op 25-07-2013 02:08:59 ]
Fervent tegenstander van het korps lasergamers.
Inderdaad.quote:
Goed, ook ik lees de Portugese wikipedia eens door.
[ afbeelding ]
Dus:
(a + b)(a4 - a3b + (ab)2 - ab3 + b4) = a5 + b5
Dan rest ons het ontbinden van (a4 - a3b + (ab)2 - ab3 + b4) in factoren..
Ik zal hier maar even iets nuttigs plaatsen..quote:
Je stelt dat gymnasten hier geen moeite mee zouden hebben, halverwege de vorige eeuw. Nu trek ik mij dat natuurlijk heeeel erg aan zijnde (net geen) gymnast, maar toch heb ik één vraag.
1. De machten van a en b in het antwoord, zijn deze in N, of beter gezegd, is het de bedoeling dat deze in N zijn?
[ Bericht 5% gewijzigd door Amoeba op 25-07-2013 03:12:33 ]
Fervent tegenstander van het korps lasergamers.
Ja, want het is de bedoeling te ontbinden in veeltermen in a en b. En we spreken alleen van een veelterm of polynoom in één of meer variabelen als de uitdrukking alleen niet-negatieve gehele machten van de variabele(n) bevat en verder alleen is samengesteld uit constanten met gebruikmaking van uitsluitend (een eindig aantal) optellingen, aftrekkingen en vermenigvuldigingen.quote:
[..]
Ik zal hier maar even iets nuttigs plaatsen..
Je stelt dat gymnasten hier geen moeite mee zouden hebben, halverwege de vorige eeuw. Nu trek ik mij dat natuurlijk heeeel erg aan zijnde (net geen) gymnast, maar toch heb ik één vraag.
1. De machten van a en b in het antwoord, zijn deze in N, of beter gezegd, is het de bedoeling dat deze in N zijn?
Weer wat geleerd. Ik zat de hele tijd te prutsen met ((a-b)(a+b))2, maar dat lijkt niet de juiste weg.quote:
[..]
Ja, want het is de bedoeling te ontbinden in veeltermen in a en b. En we spreken alleen van een veelterm of polynoom in één of meer variabelen als de uitdrukking alleen niet-negatieve gehele machten van de variabele(n) bevat en verder alleen is samengesteld uit constanten met gebruikmaking van uitsluitend optelling, aftrekking en vermenigvuldiging.
Fervent tegenstander van het korps lasergamers.
Als iemand 't praktisch vindt:
a5 + b5 = (a+b)((a3 - b3)(a-b)+(ab)2)
[ Bericht 28% gewijzigd door Amoeba op 25-07-2013 04:10:00 ]
a5 + b5 = (a+b)((a3 - b3)(a-b)+(ab)2)
[ Bericht 28% gewijzigd door Amoeba op 25-07-2013 04:10:00 ]
Fervent tegenstander van het korps lasergamers.
Ik dacht al dat je iets dergelijks zou zeggenquote:
[..]
Er is niets onbegrijpelijks aan, en ik denk dat een beetje HBS'er of gymnasiast hier pakweg een eeuw geleden of zelfs een halve eeuw geleden geen moeite mee zou hebben gehad.
[...]
Ik realiseer me dat dit stof is die ik me nooit helemaal eigen heb gemaakt, en dat was ook niet nodig: voor wiskunde heb ik zonder moeite prima cijfers gehaald op de middelbare school. Als ik nu wat minder elementaire wiskunde probeer te doen (bijvoorbeeld die Putnam problemen waar ik laatst al wat over gepost heb) loop ik wel vaak tegen dit soort dingen aan.
Ik doelde overigens niet specifiek de identiteiten op die pagina hoewel
toch wel een beetje weergeeft wat ik bedoel. Hoewel ik zelf een lichte aversie heb tegen mensen die bij elke identiteit roepen dat het magie is, heb ik bij sommige identiteiten datzelfde gevoel ook wel een beetje. Ik bedoel maar: ik kan de formule controleren en zo begrijpen dat de formule klopt, maar als ik de opdracht had om een derdemacht te schrijven als het verschil van twee kwadraten, denk ik niet dat ik met die identiteit op de proppen zou kunnen komen.
Dit geldt overigens alleen voor oneven nquote:
Wat doe je precies om tot de 2e stap toe te komen?quote:a4 − a2b2 + b4 = (a2 + b2)2 − (√3·ab)2
en dit geeft
a4 − a2b2 + b4 = ((a2 + b2) + √3·ab)((a2 + b2) − √3·ab)
x²-y² = (x+y)(x-y)quote:
[..]
Wat doe je precies om tot de 2e stap toe te komen?
Je kunt a^6=-b^6 gewoon opschrijven als (a/b)^6=-1 en dit oplossen. Dan kun je a^6+b^6 opschrijven als het product van al zijn complexe nulpunten, dit kan vanwege de hoofdstelling van de algebra. Je kunt sommige van die factoren met elkaar vermenigvuldigen en dan vind je ook de uitdrukking die je zocht.quote:
[..]
Die gaat alleen over complexe variabelen, en geeft alleen aan dat zo'n ontbinding bestaat, niet wat deze is (en volgens mij niet eens dat deze uniek is, maar dat weet ik niet helemaal zeker).
Zo kun jij bijvoorbeeld vinden dat:
[ Bericht 8% gewijzigd door Mathemaat op 25-07-2013 15:17:23 ]
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Nu begrijp ik pas wat je bedoelt, en ja, nu je die ontbinding hebt gevonden kan ik moeilijk meer beweren dat je er niks aan hebtquote:
[..]
Je kunt a^6=-b^6 gewoon opschrijven als (a/b)^6=-1 en dit oplossen. Dan kun je a^6+b^6 opschrijven als het product van al zijn complexe nulpunten, dit kan vanwege de hoofdstelling van de algebra. Je kunt sommige van die factoren met elkaar vermenigvuldigen en dan vind je ook de uitdrukking die je zocht.
Zo kun jij bijvoorbeeld vinden dat:
Nice, ik kom bij gebruik maken van de techniek in post #141 uit opquote:
[..]
Je kunt a^6=-b^6 gewoon opschrijven als (a/b)^6=-1 en dit oplossen. Dan kun je a^6+b^6 opschrijven als het product van al zijn complexe nulpunten, dit kan vanwege de hoofdstelling van de algebra. Je kunt sommige van die factoren met elkaar vermenigvuldigen en dan vind je ook de uitdrukking die je zocht.
Zo kun jij bijvoorbeeld vinden dat:
wat natuurlijk hetzelfde is.
Nee, je maakt een tekenfout. De oplossing van Mathemaat klopt wel. Je zou moeten vindenquote:Op donderdag 25 juli 2013 22:18 schreef VanishedEntity het volgende:
[..]
Nice, ik kom bij gebruik maken van de techniek in post #141 uit op,
wat natuurlijk hetzelfde is.
Dammit... Foiled by sign swapping againquote:
[..]
Nee, je maakt een tekenfout. De oplossing van Mathemaat klopt wel. Je zou moeten vinden
Anywayz, dan vind ik
persoonlijk eleganter.
Die opmerking was natuurlijk niet aan jou persoonlijk gericht. Vroeger werd er op school veel meer aandacht besteed aan het verwerven van goede algebraïsche vaardigheden. Dat kun je goed zien als je oude algebra boekjes bekijkt, bijvoorbeeld op de site van het Nederlands schoolmuseum. Toen was algebra ook een apart schoolvak. Tegenwoordig vindt men die vaardigheden niet meer zo nodig, maar ten onrechte: bij veel vervolgopleidingen heb je het gewoon nodig, en ook als je wat verder wil met wiskunde is het onmisbaar.quote:
[..]
Ik dacht al dat je iets dergelijks zou zeggen
Ik realiseer me dat dit stof is die ik me nooit helemaal eigen heb gemaakt, en dat was ook niet nodig: voor wiskunde heb ik zonder moeite prima cijfers gehaald op de middelbare school. Als ik nu wat minder elementaire wiskunde probeer te doen (bijvoorbeeld die Putnam problemen waar ik laatst al wat over gepost heb) loop ik wel vaak tegen dit soort dingen aan.
Het is veel eenvoudiger dan het er op het eerste gezicht uitziet. Dit is een kleine variatie op de oeroude Babylonische truc (zie hier) om een rechthoek te transformeren tot een L-vorm die bestaat uit een vierkant waaraan in één hoek een kleiner vierkant ontbreekt.quote:Ik doelde overigens niet specifiek de identiteiten op die pagina hoewel
[ afbeelding ]
toch wel een beetje weergeeft wat ik bedoel. Hoewel ik zelf een lichte aversie heb tegen mensen die bij elke identiteit roepen dat het magie is, heb ik bij sommige identiteiten datzelfde gevoel ook wel een beetje. Ik bedoel maar: ik kan de formule controleren en zo begrijpen dat de formule klopt, maar als ik de opdracht had om een derdemacht te schrijven als het verschil van twee kwadraten, denk ik niet dat ik met die identiteit op de proppen zou kunnen komen.
Stel we hebben een rechthoekig stuk land met lengte a en breedte b, dan is het gemiddelde van de lengte en de breedte ½(a + b). We kunnen dit gemiddelde uiteraard krijgen door hetzij de helft van het verschil (a − b) van a af te halen, dus ½(a + b) = a − ½(a − b) hetzij de helft van het verschil bij b op te tellen, dus ½(a + b) = b + ½(a − b). Als we dus van de lengte van de rechthoek een strook af halen van b bij ½(a − b) en deze aan de breedte toevoegen, dan hebben we een L-vormige figuur die bestaat uit een vierkant waarvan de zijde gelijk is aan het gemiddelde ½(a + b) en waaraan in één hoekpunt een kleiner vierkant met een zijde gelijk aan het halve verschil ½(a − b) ontbreekt, zodat
ab = (½(a + b))2 − (½(a − b))2
Bedenk je dan dat a3 = a·a2 en substitueer je b = a2, dan heb je
a3 = (½(a + a2))2 − (½(a − a2))2
en dat is in wezen dezelfde identiteit.
Inderdaad.quote:[..]
Dit geldt overigens alleen voor oneven n
Riparius, nu de oplossing van de opgave bekend is zou ik wel eens willen weten welk merkwaardig product in aanmerking komt om a^4 - a^3b +(ab)^2 - ab^3 + b^4 te ontbinden. Ik heb verleden nacht daar mijn hoofd over gebroken, maar ik zie het niet.
Fervent tegenstander van het korps lasergamers.
En ik begrijp niet helemaal hoe je (a/b)^5 = -1 oplost in C Waar ik overigens het gevoel heb dat ik dit wel zou moeten kunnen.quote:
[..]
Je kunt a^6=-b^6 gewoon opschrijven als (a/b)^6=-1 en dit oplossen. Dan kun je a^6+b^6 opschrijven als het product van al zijn complexe nulpunten, dit kan vanwege de hoofdstelling van de algebra. Je kunt sommige van die factoren met elkaar vermenigvuldigen en dan vind je ook de uitdrukking die je zocht.
Zo kun jij bijvoorbeeld vinden dat:
Fervent tegenstander van het korps lasergamers.
Zoals inmiddels duidelijk is kun je a5 + b5 ontbinden door a/b = z oftewel a = bz te substitueren, zodatquote:
Riparius, nu de oplossing van de opgave bekend is zou ik wel eens willen weten welk merkwaardig product in aanmerking komt om a^4 - a^3b +(ab)^2 - ab^3 + b^4 te ontbinden. Ik heb verleden nacht daar mijn hoofd over gebroken, maar ik zie het niet.
a5 + b5 = b5(z5 + 1).
Dan komt het ontbinden neer op het vinden van de (lineaire) factoren van z5 + 1 en dus het oplossen in C van de vergelijking z5 + 1 = 0.
Complexe wortels van een algebraïsche vergelijking met reële coëfficiënten treden altijd op als geconjugeerde paren, en omdat som en product van twee geconjugeerde complexe getallen reëel zijn, levert elk paar geconjugeerde wortels van de vergelijking dan een kwadratische factor op met reële coëfficiënten. Immers, als z1 en z2 twee toegevoegd complexe wortels zijn van de vergelijking z5 + 1 = 0, dan bevat z5 + 1 een factor (z − z1) en een factor (z − z2) en dus een kwadratische factor (z − z1)(z − z2) = z2 − (z1 + z2)z + z1z2 waarvan de coëfficiënten reëel zijn. Maar om deze werkwijze te gebruiken moet je wel iets van complexe getallen weten en moet je ook in staat zijn de vergelijking z5 + 1 = 0 algebraïsch op te lossen.
Zoals gezegd is het ook mogelijk a4 − a3b + a2b2 − ab3 + b4 met louter elementaire (school)algebra te ontbinden in veeltermen in a en b met reële coëfficiënten. Dit gaat als volgt.
We beginnen weer met kwadraatafsplitsing, toegepast op de termen met een positief teken. Aangezien (a2 + b2)2 = a4 + 2a2b2 + b4 hebben we a4 + a2b2 + b4 = (a2 + b2)2 − a2b2 en dus
a4 − a3b + a2b2 − ab3 + b4 = (a2 + b2)2 − a3b − ab3 − a2b2
Nu is het de bedoeling de uitdrukking in het rechterlid uiteindelijk te herleiden tot een verschil van twee kwadraten. De termen (a2 + b2)2 en a2b2 zijn al kwadraten, dus die laat ik nu even staan. Bij de termen a3b en ab3 kan ik een factor ab buiten haakjes halen zodat binnen haakjes (a2 + b2) overblijft. Dan hebben we
a4 − a3b + a2b2 − ab3 + b4 = (a2 + b2)2 − ab(a2 + b2) − a2b2
Nu kunnen we nogmaals kwadraatafsplitsing toepassen op (a2 + b2)2 − ab(a2 + b2). Stel om dit gemakkelijker te zien even a2 + b2 = p, dan hebben we p2 − ab·p = (p −½ab)2 − (½ab)2, zodat we dus krijgen
a4 − a3b + a2b2 − ab3 + b4 = ((a2 + b2) − ½ab)2 − (½ab)2 − a2b2
en dus
a4 − a3b + a2b2 − ab3 + b4 = (a2 − ½ab + b2)2 − (5/4)·a2b2
Nu is ook (5/4)·a2b2 = (½√5·ab)2 zodat we hebben
a4 − a3b + a2b2 − ab3 + b4 = (a2 − ½ab + b2)2 − (½√5·ab)2
waarmee de uitdrukking is herleid tot een verschil van twee kwadraten. Hiervoor kunnen we nu schrijven
a4 − a3b + a2b2 − ab3 + b4 = ((a2 − ½ab + b2) − ½√5·ab)((a2 − ½ab + b2) + ½√5·ab)
oftewel
a4 − a3b + a2b2 − ab3 + b4 = (a2 − (½ + ½√5)ab + b2)(a2 − (½ − ½√5)ab + b2)
QED
[ Bericht 0% gewijzigd door Riparius op 26-07-2013 14:24:20 ]
Wanneer ik heb dat:
z5 = -1 = eπ i
|z5| = 1
Krijg ik voor mijn oplossingen in C:
z = e(π/5 + k*2/5π) i
z = eπ/5 i
z = e3π/5 i
z = e5π/5 i
z = e7π/5 i
z = e9π/5 i
z = cos(0) + i sin(0) = 1
z = cos(2π/5) + i sin(2π/5)
z = cos(4π/5) + i sin(4π/5)
z = cos(6π/5) + i sin(6π/5)
z = cos(8π/5) + i sin(8π/5)
Ik ken alleen geen exacte uitdrukkingen hiervoor.
[ Bericht 4% gewijzigd door Amoeba op 26-07-2013 03:02:54 ]
z5 = -1 = eπ i
|z5| = 1
Krijg ik voor mijn oplossingen in C:
z = e(π/5 + k*2/5π) i
z = eπ/5 i
z = e3π/5 i
z = e5π/5 i
z = e7π/5 i
z = e9π/5 i
z = cos(0) + i sin(0) = 1
z = cos(2π/5) + i sin(2π/5)
z = cos(4π/5) + i sin(4π/5)
z = cos(6π/5) + i sin(6π/5)
z = cos(8π/5) + i sin(8π/5)
Ik ken alleen geen exacte uitdrukkingen hiervoor.
[ Bericht 4% gewijzigd door Amoeba op 26-07-2013 03:02:54 ]
Fervent tegenstander van het korps lasergamers.
Substitutie van a/b = z oftewel a = bz geeftquote:
[..]
En ik begrijp niet helemaal hoe je (a/b)^5 = -1 oplost in C Waar ik overigens het gevoel heb dat ik dit wel zou moeten kunnen.
a5 + b5 = b5(z5 + 1)
zodat ontbinden neer komt op het vinden van de (lineaire) factoren van z5 + 1 en dus het oplossen in C van de vergelijking
z5 + 1 = 0
We zien dat z = −1 een oplossing is van deze vergelijking zodat z5 + 1 een factor (z + 1) bevat. Uitvoeren van een polynoomstaardeling levert dan op dat we kunnen schrijven
(z + 1)(z4 − z3 + z2 − z + 1) = 0
zodat we om de overige vier wortels van de vergelijking z5 + 1 = 0 te vinden nog de vierdegraadsvergelijking
z4 − z3 + z2 − z + 1 = 0
op moeten lossen. Dit kun je op verschillende manieren doen. Om te beginnen kun je hier op een volkomen analoge manier te werk gaan als ik hierboven laat zien voor de ontbinding van a4 − a3b + a2b2 − ab3 + b4. Dan pas je dus tweemaal kwadraatafsplitsing toe om het vierdegraadspolynoom in het linkerlid te herleiden tot een product van twee kwadratische polynomen, waarna je alleen nog twee vierkantsvergelijkingen op hoeft te lossen.
Een andere manier om deze vergelijking op te lossen is middels een geschikt gekozen substitutie. We hebben hier van doen met een zogeheten wederkerige vergelijking van even graad, en deze zijn te herleiden tot een vergelijking waarvan de graad nog slechts de helft van de graad van de oorspronkelijke vergelijking bedraagt. Op de theorie van de wederkerige vergelijkingen ga ik hier niet in, daar heb ik je namelijk al eens een keer iets over uitgelegd. Delen we beide leden door z2 (hetgeen is toegestaan aangezien z = 0 geen wortel is van de vergelijking) dan krijgen we
z2 - z + 1 − 1/z + 1/z2 = 0
waarvoor we kunnen schrijven
(z + 1/z)2 − (z + 1/z) − 1 = 0
en substutie w = z + 1/z geeft dan
w2 − w − 1 = 0
Dit is een vierkantsvergelijking met als wortels w1,2 = ½ ± ½√5 zodat je nu alleen nog de vergelijkingen z + 1/z = ½ + ½√5 en z + 1/z = ½ − ½√5 hoeft op te lossen, oftewel we hebben
z2 − (½ + ½√5)z + 1 = 0 ∨ z2 − (½ − ½√5)z + 1 = 0
Een heel andere manier om de vergelijking z5 + 1 = 0 op te lossen is gebruik te maken van de formule van De Moivre
(cos φ + i·sin φ)n = cos nφ + i·sin nφ
Op grond hiervan is het direct duidelijk dat de vijf wortels van de vergelijking zijn te schrijven als
zk = cos((2k − 1)π/5) + i·sin((2k − 1)π/5), k = 1..5
en met behulp van de formule van Euler kun je dit ook compacter schrijven als
zk = ei·(2k − 1)π/5, k = 1..5
Nu zie je dat z1 = ei·π/5 en z5 = ei·9π/5 = e−i·π/5 toegevoegd complex zijn, zodat z5 + 1 dus een reële kwadratische factor (z − z1)(z − z5) = (z − ei·π/5)(z − e−i·π/5) = z2 − (ei·π/5 + e−i·π/5)z + 1 bevat, oftewel een kwadratische factor
z2 − 2·cos(π/5)·z + 1
Evenzo zijn z2 en z4 toegevoegd complex, en deze leveren een reële kwadratische factor
z2 − 2·cos(3π/5)·z + 1
De eerste van deze kwadratische factoren correspondeert met z2 − (½ + ½√5)z + 1 en de tweede met z2 − (½ − ½√5)z + 1, zodat we hebben
cos(π/5) = ¼ + ¼√5, cos(3π/5) = ¼ − ¼√5
We kunnen dus de ontbinding van a5 + b5 in veeltermen in a en b met reële coëfficiënten ook als volgt schrijven in goniometrische vorm
a5 + b5 = (a + b)(a2 − 2ab·cos(π/5) + b2)(a2 − 2ab·cos(3π/5) + b2)
Het is in het algemeen mogelijk zowel an − bn als an + bn voor n > 2 te schrijven in een dergelijke goniometrische vorm als een product van lineaire en kwadratische veeltermen in a en b met reële coëfficiënten, waarbij de kwadratische veeltermen doen denken aan de cosinusregel c2 = a2 − 2ab·cos γ + b2. De overeenstemming met de cosinusregel is niet toevallig maar wordt inzichtelijk door het zogeheten cirkeltheorema van Cotes.
quote:
[..]De 2 hoofdstukken die ik heb gehad over complexe getallen beschreven inderdaad de formule van de Moive en de formule van Euler, vandaar dat ik die e-machten (met wat moeite) ook had weten te produceren. Daarnaast wat rekenen met complexe getallen i.c.m. de natuurkunde, recursieve formules etc. Ik vind het uitermate storend dat mijn geheugen niet beter in staat is om die technieken wat beter te onthouden dan half.SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.
Het oplossen van een vierdegraadsvergelijking hebben we echter niet behandeld. Het hoofdstuk bleef beperkt tot het oplossen van een gereduceerde kubische vergelijking, en incidenteel een kubische vergelijking, door middel van een geschikte substitutie. Volgens mij heb je me inderdaad ooit iets uitgelegd over wederkerige vergelijkingen toen we het probleem behandelden van die bol met een doorsnede a waarbij beide stukken die samen een halve bol vormden een gelijke inhoud hebben. Dat is alweer 'n poosje geleden, maar dat was deze post:SPOILEROm spoilers te kunnen lezen moet je zijn ingelogd. Je moet je daarvoor eerst gratis Registreren. Ook kun je spoilers niet lezen als je een ban hebt.Wat betreft de techniek van het kwadraatafsplitsen, dit lijkt me nou een typisch gevalletje oefening baart kunst. Het ongeoefende oog ziet de juiste aanpak van zo'n probleem nu eenmaal minder snel..Fervent tegenstander van het korps lasergamers.
Even wat heel anders. Ik probeerde deze opgave te maken:
Laat d1 t/m d12 reële getallen in het open interval (1, 12) zijn. Laat zien dat er verschillende indices i, j, k bestaan zodat di, dj en dk de lengtes van de zijden van een 'acute triangle' (een driehoek waarvan alle hoeken minder dan 90 graden zijn) zijn.
Ik stelde vervolgens de voorwaarden op dat drie gegeven reële getallen de lengtes van de zijden van een 'acute triangle' zijn. Neem c ≥ b ≥ a. Dan is a2 + b2 > c2 een belangrijke voorwaarde, maar er moet ook gelden dat c < a + b, anders is er geen sprake van een driehoek.
Neem nu dk = 1012-k, met 1 ≤ k ≤ 12 Volgens mij bestaat er dan geen driehoek waarvan de zijden gelijk zijn aan een drietal van deze dk's.
De dk's worden dus steeds een factor 10 groter. Het is niet mogelijk een driehoek te tekenen met zijden van lengte a, b en c zodat c > 10b en b > 10a.
In het antwoord wordt de voorwaarde a + b > c helemaal niet genoemd.
Ik heb de vraag hier vandaan en de antwoorden hier.
Begrijp ik iets niet of klopt de vraag niet? Dat zou me nogal verbazen, het is best wel een prestigieuze wedstrijd had ik het idee.
Laat d1 t/m d12 reële getallen in het open interval (1, 12) zijn. Laat zien dat er verschillende indices i, j, k bestaan zodat di, dj en dk de lengtes van de zijden van een 'acute triangle' (een driehoek waarvan alle hoeken minder dan 90 graden zijn) zijn.
Ik stelde vervolgens de voorwaarden op dat drie gegeven reële getallen de lengtes van de zijden van een 'acute triangle' zijn. Neem c ≥ b ≥ a. Dan is a2 + b2 > c2 een belangrijke voorwaarde, maar er moet ook gelden dat c < a + b, anders is er geen sprake van een driehoek.
Neem nu dk = 1012-k, met 1 ≤ k ≤ 12 Volgens mij bestaat er dan geen driehoek waarvan de zijden gelijk zijn aan een drietal van deze dk's.
De dk's worden dus steeds een factor 10 groter. Het is niet mogelijk een driehoek te tekenen met zijden van lengte a, b en c zodat c > 10b en b > 10a.
In het antwoord wordt de voorwaarde a + b > c helemaal niet genoemd.
Ik heb de vraag hier vandaan en de antwoorden hier.
Begrijp ik iets niet of klopt de vraag niet? Dat zou me nogal verbazen, het is best wel een prestigieuze wedstrijd had ik het idee.
Jouw dk -tjes zitten niet allemaal in (1,12)quote:
Even wat heel anders. Ik probeerde deze opgave te maken:
Laat d1 t/m d12 reële getallen in het open interval (1, 12) zijn. Laat zien dat er verschillende indices i, j, k bestaan zodat di, dj en dk de lengtes van de zijden van een 'acute triangle' (een driehoek waarvan alle hoeken minder dan 90 graden zijn) zijn.
Ik stelde vervolgens de voorwaarden op dat drie gegeven reële getallen de lengtes van de zijden van een 'acute triangle' zijn. Neem c ≥ b ≥ a. Dan is a2 + b2 > c2 een belangrijke voorwaarde, maar er moet ook gelden dat c < a + b, anders is er geen sprake van een driehoek.
Neem nu dk = 1012-k, met 1 ≤ k ≤ 12 Volgens mij bestaat er dan geen driehoek waarvan de zijden gelijk zijn aan een drietal van deze dk's.
De dk's worden dus steeds een factor 10 groter. Het is niet mogelijk een driehoek te tekenen met zijden van lengte a, b en c zodat c > 10b en b > 10a.
In het antwoord wordt de voorwaarde a + b > c helemaal niet genoemd.
Ik heb de vraag hier vandaan en de antwoorden hier.
Begrijp ik iets niet of klopt de vraag niet? Dat zou me nogal verbazen, het is best wel een prestigieuze wedstrijd had ik het idee.
Nee, maar dat is ook niet nodig, want als je c ≥ b ≥ a > 0 hebt en tevens c2 < a2 + b2, dan is ook c2 < (a + b)2 aangezien a2 + b2 < (a + b)2 en dus c < a + b. Handig hè, die merkwaardige producten?quote:
In het antwoord wordt de voorwaarde a + b > c helemaal niet genoemd.
Ik begrijp de relatie tussen de vraag en het antwoord niet. M.i. bewijst het antwoord iets anders dan er gevraagd wordt.quote:Ik heb de vraag hier vandaan en de antwoorden hier.
Begrijp ik iets niet of klopt de vraag niet? Dat zou me nogal verbazen, het is best wel een prestigieuze wedstrijd had ik het idee.
Er is een i<= 10 zodat ofwelquote:
Ik begrijp de relatie tussen de vraag en het antwoord niet. M.i. bewijst het antwoord iets anders dan er gevraagd wordt.
di+2² < di² + di+1²
en je dus een acute triangle hebt, ofwel krijg je tegenspraak met het feit dat alle dk'tjes in (1,12) zitten.
O, god, wat ben ik dom bezigquote:
[..]
Jouw dk -tjes zitten niet allemaal in (1,12)
Misschien moet ik eerst maar leren lezen voor ik wiskunde probeer...Anyway, thanks!
Je hebt een punt jaquote:
[..]
Nee, maar dat is ook niet nodig, want als je c ≥ b ≥ a > 0 hebt en tevens c2 < a2 + b2, dan is ook c2 < (a + b)2 aangezien a2 + b2 < (a + b)2 en dus c < a + b. Handig hè, die merkwaardige producten?
Ah, ik geloof dat ik het nu zie. Het is een bewijs uit het ongerijmde. Als er geen drietal waarden di dj dk op het open interval (1,12) zou zijn die de zijden van een scherpe driehoek vormen, dan moet je hebben di+2² ≥ di² + di+1² voor 1 ≤ i ≤ 10 en dan heb je d12² ≥ 144·d1² en dat is in tegenspraak met 1 < d1 ≤ d12 < 12, QED.quote:
[..]
Er is een i<= 10 zodat ofwel
di+2² < di² + di+1²
en je dus een acute triangle hebt, ofwel krijg je tegenspraak met het feit dat alle dk'tjes in (1,12) zitten.
5050/2525 = (502/25)25 = (2500/25)25 = 10025quote:
50 50 / 25 25 = 100 25
Hoe kom je aan 100?
Waaraan is 8 8 gelijk?
Derde macht van 4 4
Waarom?
De rest van je vragen is uiterst wazig.
Je hebt de rekenregels voor machten nodig.
Ofwel (ap)q = apq
En:
ap/bp =(a/b)p
Je zou kunnen gebruiken dat 8 = 23 en 4 = 22
[ Bericht 6% gewijzigd door Amoeba op 27-07-2013 15:19:20 ]
Fervent tegenstander van het korps lasergamers.
Waaraan is 8^8 gelijk?quote:
[..]
5050/2525 = (502/25)25 = (2500/25)25 = 10025
De rest van je vragen is uiterst wazig.
Je hebt de rekenregels voor machten nodig.
Ofwel (ap)q = apq
En:
ap/bp =(a/b)p
Je zou kunnen gebruiken dat 8 = 23 en 4
a. de tweede macht van 4^4
b. de derde macht van 4^4
c. de vierde macht van 4^4
d. de achtste macht van 4^4
e. de zestiende macht van 4^4
Lees je wel wat ik zeg? Ga het eens uitrekenen dan.quote:
[..]
Waaraan is 8^8 gelijk?
a. de tweede macht van 4^4
b. de derde macht van 4^4
c. de vierde macht van 4^4
d. de achtste macht van 4^4
e. de zestiende macht van 4^4
Fervent tegenstander van het korps lasergamers.
88 = (23)8 = 224 = 22*12 = 412 = (44)3
Zie je wat ik steeds doe? Ik maak gebruik van de rekenregels voor machten. Die ga ik niet nog eens herhalen, daar ze pakweg 3 posts hierboven benoemd zijn.
Zie je wat ik steeds doe? Ik maak gebruik van de rekenregels voor machten. Die ga ik niet nog eens herhalen, daar ze pakweg 3 posts hierboven benoemd zijn.
Fervent tegenstander van het korps lasergamers.
Dit kan je dus gewoon invoeren in wolfram alpha of zelfs google. Ik moet zeggen dat mijn vraag gister ook niet van veel inzicht getuigde, maar iets intypen in google bespaart zowel jou als de mensen die reageren op je posts moeite.quote:
[..]
Waaraan is 8^8 gelijk?
a. de tweede macht van 4^4
b. de derde macht van 4^4
c. de vierde macht van 4^4
d. de achtste macht van 4^4
e. de zestiende macht van 4^4
Nee dit is geen constructieve kritiek. Wiskundenoob (toepasselijke naam..) moet duidelijk leren hoe hij dit soort problemen aanpakt, en dus inzicht in de wiskunde verkrijgen. Iets simpel invoeren in WolframAlpha of Google lijkt wel heel veel op het gebruiken van de (door Riparius) zo verfoeide grafische rekenmachine. Verder voeg je m.i. wel degelijk wat toe aan het topic, dus zeer welkom.quote:Op zaterdag 27 juli 2013 17:49 schreef randomo het volgende:
[..]
Dit kan je dus gewoon invoeren in wolfram alpha of zelfs google. Ik moet zeggen dat mijn vraag gister ook niet van veel inzicht getuigde, maar iets intypen in google bespaart zowel jou als de mensen die reageren op je posts moeite.
[ Bericht 2% gewijzigd door Amoeba op 27-07-2013 18:51:37 ]
Fervent tegenstander van het korps lasergamers.
Als je een vlakdeel hebt dat wordt ingesloten door een grafiek, de x-as en de y-as, en je wil de inhoud weten als je het om een as wentelt, dan maakt het toch niet uit om welke as je hem wentelt? Of denk ik nou te simpel?
Gist is liefde, gist is leven. Vooral in een vagijn.
Alleen als de formule luidt y = x, dan maakt het niets uit. Anders wel.quote:
Als je een vlakdeel hebt dat wordt ingesloten door een grafiek, de x-as en de y-as, en je wil de inhoud weten als je het om een as wentelt, dan maakt het toch niet uit om welke as je hem wentelt? Of denk ik nou te simpel?
Fervent tegenstander van het korps lasergamers.
Het probleem is niet dat je te simpel denkt maar dat je er kennelijk helemaal niet over na hebt gedacht. Beschouw het vlakdeel begrensd door de positieve x-as, de positieve y-as, en de rechte lijn met vergelijking y = −2x + 1. Deze lijn snijdt de x-as in het punt (½; 0) en de y-as in het punt (0; 1). Bij wenteling van dit vlakdeel om de x-as krijg je een kegel waarvan de straal r van het grondvlak gelijk is aan 1 en de hoogte h gelijk is aan ½. Maar bij wenteling om de y-as krijg je een kegel met r = ½ en h = 1. De vraag is dan of jij denkt dat deze kegels dezelfde inhoud hebben?quote:
Als je een vlakdeel hebt dat wordt ingesloten door een grafiek, de x-as en de y-as, en je wil de inhoud weten als je het om een as wentelt, dan maakt het toch niet uit om welke as je hem wentelt? Of denk ik nou te simpel?
Wat denk je van het vlakdeel begrensd door de positieve x-as, de positieve y-as, en de curve met vergelijking x2 + y2 = 1 ?quote:
[..]
Alleen als de formule luidt y = x, dan maakt het niets uit. Anders wel.
Kutquote:
[..]
Wat denk je van het vlakdeel begrensd door de positieve x-as, de positieve y-as, en de curve met vergelijking x2 + y2 = 1 ?
Enfin, je snapt wat ik bedoel TS. Enkel bij functies die symmetrisch zijn in y = x. Zeg ik dit juist Riparius?
Fervent tegenstander van het korps lasergamers.
Nee, natuurlijk niet, want r² leveren andere waardes op. Je hebt gelijk.quote:
[..]
Het probleem is niet dat je te simpel denkt maar dat je er kennelijk helemaal niet over na hebt gedacht. Beschouw het vlakdeel begrensd door de positieve x-as, de positieve y-as, en de rechte lijn met vergelijking y = −2x + 1. Deze lijn snijdt de x-as in het punt (½; 0) en de y-as in het punt (0; 1). Bij wenteling van dit vlakdeel om de x-as krijg je een kegel waarvan de straal r van het grondvlak gelijk is aan 1 en de hoogte h gelijk is aan ½. Maar bij wenteling om de y-as krijg je een kegel met r = ½ en h = 1. De vraag is dan of jij denkt dat deze kegels dezelfde inhoud hebben?
Ik denk dat ik al weet waar het fout ging, ik moest een vlakdeel om de y-as wentelen waarbij de 'straal' die delta x geeft gelijk was aan de 'straal' die delta y gaf.
Gist is liefde, gist is leven. Vooral in een vagijn.
Nee. Je bedoelt dat de grafiek spiegelsymmetrisch is t.o.v. de lijn y = x. Het hoeft niet eens een grafiek van een functie te zijn, denk bijvoorbeeld aan twee rechte lijnstukken tussen de punten (1; 0) en (1; 1) en tussen de punten (0; 1) en (1; 1).quote:
[..]
Kut
Enfin, je snapt wat ik bedoel TS. Enkel bij functies die symmetrisch zijn in y = x. Zeg ik dit juist Riparius?
Ah ja. Ik had al het idee dat 't niet helemaal klopte wat ik zei, maar dat bedoelde ik inderdaad.quote:
[..]
Nee. Je bedoelt dat de grafiek spiegelsymmetrisch is t.o.v. de lijn y = x. Het hoeft niet eens een grafiek van een functie te zijn, denk bijvoorbeeld aan twee rechte lijnstukken tussen de punten (1; 0) en (1;1) en tussen de punten (0; 1) en (1; 1).
Fervent tegenstander van het korps lasergamers.
Dat klopt, maar dan stelt hij de verkeerde vragen. Het antwoord op zijn vraag is makkelijk met een rekenmachine of iets dergelijks te controleren, maar inzicht in het rekenen met machten zal hij daar niet van krijgen.quote:
[..]
Nee dit is geen constructieve kritiek. Wiskundenoob (toepasselijke naam..) moet duidelijk leren hoe hij dit soort problemen aanpakt, en dus inzicht in de wiskunde verkrijgen. Iets simpel invoeren in WolframAlpha of Google lijkt wel heel veel op het gebruiken van de (door Riparius) zo verfoeide grafische rekenmachine. Verder voeg je m.i. wel degelijk wat toe aan het topic, dus zeer welkom.
De grafiek hoeft zelfs niet spiegelsymmetrisch t.o.v. y=x te zijn om het wentelen om de x en y-as tot dezelfde inhoud te laten leiden.quote:
[..]
Nee. Je bedoelt dat de grafiek spiegelsymmetrisch is t.o.v. de lijn y = x. Het hoeft niet eens een grafiek van een functie te zijn, denk bijvoorbeeld aan twee rechte lijnstukken tussen de punten (1; 0) en (1; 1) en tussen de punten (0; 1) en (1; 1).
Beschouw bijvoorbeeld de twee rechthoeken met als hoekpunten
(0,0), (0,1), (3,0), (3,1) en (0,2), (0,3), (3,2), (3,3).
Wentelen om de x-as en y-as geeft beide een inhoud van 18 pi, maar het is niet spiegelsymmetrisch in y=x.
Dat is juist, spiegelsymmetrie van het vlakdeel t.o.v. de lijn y = x is een voldoende maar geen noodzakelijke voorwaarde voor gelijke volumina van de omwentelingslichamen bij wenteling om de x-as resp. de y-as. In jouw voorbeeld ligt echter het zwaartepunt (1½; 1½) van het vlakdeel wel degelijk op de lijn y = x, zodat volgens het tweede theorema van Pappus-Guldin de volumina bij wenteling om de x-as resp. de y-as gelijk moeten zijn. De oppervlakte van je vlakdeel is 6 en het zwaartepunt beschijft bij wenteling om de x-as of de y-as een cirkel met omtrek 3π, zodat het volume in beide gevallen inderdaad 6·3π = 18π bedraagt. De ligging van het zwaartepunt van het vlakdeel op de lijn y = x is zowel een noodzakelijke als een voldoende voorwaarde voor gelijke volumina van de omwentelingslichamen bij wenteling om de x-as resp. de y-as, en aan deze voorwaarde is uiteraard voldaan bij een vlakdeel dat spiegelsymmetrisch is t.o.v. de lijn y = x, aangezien het zwaartepunt op de symmetrie-as ligt.quote:
[..]
De grafiek hoeft zelfs niet spiegelsymmetrisch t.o.v. y=x te zijn om het wentelen om de x en y-as tot dezelfde inhoud te laten leiden.
Beschouw bijvoorbeeld de twee rechthoeken met als hoekpunten
(0,0), (0,1), (3,0), (3,1) en (0,2), (0,3), (3,2), (3,3).
Wentelen om de x-as en y-as geeft beide een inhoud van 18 pi, maar het is niet spiegelsymmetrisch in y=x.
Je ziet toch dat ik het exact aan kan tonen zonder gebruik van een calculator. Dan snap ik even niet waarom dit geen inzicht verschaft in het rekenen met machten.quote:
[..]
Dat klopt, maar dan stelt hij de verkeerde vragen. Het antwoord op zijn vraag is makkelijk met een rekenmachine of iets dergelijks te controleren, maar inzicht in het rekenen met machten zal hij daar niet van krijgen.
Fervent tegenstander van het korps lasergamers.
Didactiek is ook een vak. Uiteraard is je herleiding hierboven correct, maar het is de vraag hoeveel hij hier van opsteekt gezien zijn 'voorkennis' en track record van zijn eerdere posts in dit topic.quote:
[..]
Je ziet toch dat ik het exact aan kan tonen zonder gebruik van een calculator. Dan snap ik even niet waarom dit geen inzicht verschaft in het rekenen met machten.
Het valt op dat bij alle meerkeuze antwoorden sprake is van een macht van 44 en dat dus gevraagd wordt 88 te schrijven als een macht van 44. Dan is het wellicht beter voor het inzicht om te beginnen met erop te wijzen dat 4 en 8 beide machten zijn van 2, en dan eerst te laten zien dat je hebt
44 = (22)4 = 28
en
88 = (23)8 = 224
Vervolgens kun je dan stoppen met je uitleg en een wedervraag stellen om te zien of hij nu wel het juiste antwoord kan beredeneren.
Je hebt gelijk.
Anders gezegd, ook de vermenigvuldiging is commutatief en associatief, terwijl de eigenschappen e)
tot en met h) impliceren dat C \ {0} ten aanzien van de vermenigvuldiging een commutatieve groep
vormt.
Ik kan C \ {0} niet herleiden naar begrijpbare Nederlandse taal. Verder snap ik wel dat bewerkingen in C associatief en communicatief zijn.
Anders gezegd, ook de vermenigvuldiging is commutatief en associatief, terwijl de eigenschappen e)
tot en met h) impliceren dat C \ {0} ten aanzien van de vermenigvuldiging een commutatieve groep
vormt.
Ik kan C \ {0} niet herleiden naar begrijpbare Nederlandse taal. Verder snap ik wel dat bewerkingen in C associatief en communicatief zijn.
Fervent tegenstander van het korps lasergamers.
Ik begrijp echt niet waarover je het hebt. Welke eigenschappen e) t/m h) ?quote:
Je hebt gelijk.
Anders gezegd, ook de vermenigvuldiging is commutatief en associatief, terwijl de eigenschappen e)
tot en met h) impliceren dat C \ {0} ten aanzien van de vermenigvuldiging een commutatieve groep
vormt.
Ik kan C \ {0} niet herleiden naar begrijpbare Nederlandse taal. Verder snap ik wel dat bewerkingen in C associatief en communicatief zijn.
Pagina 60 van dat dictaat van Duistermaat wat je me stuurde.quote:
[..]
Ik begrijp echt niet waarover je het hebt. Welke eigenschappen e) t/m h) ?
Fervent tegenstander van het korps lasergamers.
Ah zo. De gegeven rekenregels zijn allemaal af te leiden uit de definitie van een complex getal als een geordend paar reële getallen en de daarbij gedefinieerde optelling en vermenigvuldiging van deze geordende paren.quote:
[..]
Pagina 60 van dat dictaat van Duistermaat wat je me stuurde.
Met A \ B wordt bedoeld de verzameling van alle elementen uit A die niet in B zitten. C \ {0} is dus de verzameling van alle complexe getallen uitgezonderd nul. Oftewel:
C \ {0} := {z ∈ C | z ≠ 0}
Begrijp je deze notatie? Zo nee, raadpleeg dan een boekje of dictaat over verzamelingenleer of lees dit eens goed door.
[ Bericht 0% gewijzigd door Riparius op 29-07-2013 19:48:29 ]
Ja dat kan ik wel volgen. Wederom bedankt.
Ik zal nog wel vaker problemen hebben met notaties die ik nog niet ken. 't Volgende wat problemen op gaat leveren is dat matrices nooit behandeld zijn bij mij op het vwo, iets wat ik persoonlijk als vervelend ervaar.
Heb jij toevallig ergens een schoolboekje waarin op vwo-manier die matrices goed beschreven staan, inclusief de bijbehorende iteratieve oefeningen?
Ik zal nog wel vaker problemen hebben met notaties die ik nog niet ken. 't Volgende wat problemen op gaat leveren is dat matrices nooit behandeld zijn bij mij op het vwo, iets wat ik persoonlijk als vervelend ervaar.
Heb jij toevallig ergens een schoolboekje waarin op vwo-manier die matrices goed beschreven staan, inclusief de bijbehorende iteratieve oefeningen?
Fervent tegenstander van het korps lasergamers.
Voor een eenvoudige inleiding in de lineaire algebra zou je dit dictaat kunnen gebruiken, dan leer je ook iets over matrices, inclusief oefeningen. Maar ik denk dat je dit voor een beetje complexe functietheorie niet nodig hebt, hoewel inzicht in de meetkundige interpretatie van een vermenigvuldiging met een complex getal als een draaistrekking in het complexe vlak wel essentieel is. Je kunt complexe getallen ook formeel introduceren als bepaalde 2 × 2 matrices, zoals in het dictaat is te zien. Maar ook zonder matrices is gemakkelijk in te zien dat een vermenigvuldiging metquote:
Ja dat kan ik wel volgen. Wederom bedankt.
Ik zal nog wel vaker problemen hebben met notaties die ik nog niet ken. 't Volgende wat problemen op gaat leveren is dat matrices nooit behandeld zijn bij mij op het vwo, iets wat ik persoonlijk als vervelend ervaar.
Heb jij toevallig ergens een schoolboekje waarin op vwo-manier die matrices goed beschreven staan, inclusief de bijbehorende iteratieve oefeningen?
cos φ + i·sin φ
in het complexe vlak beantwoordt aan een rotatie om de oorsprong over een hoek φ.
De inleiding klinkt veelbelovend. Dan ga ik me maar in LinAlg A verdiepen en complexe functietheorie. En ga me niet meer aanbieden, ik ga nu eerst hier m'n tanden inzetten.quote:
[..]
Voor een eenvoudige inleiding in de lineaire algebra zou je dit dictaat kunnen gebruiken, dan leer je ook iets over matrices, inclusief oefeningen. Maar ik denk dat je dit voor een beetje complexe functietheorie niet nodig hebt, hoewel inzicht in de meetkundige interpretatie van een vermenigvuldiging met een complex getal als een draaistrekking in het complexe vlak wel essentieel is. Je kunt complexe getallen ook formeel introduceren als bepaalde 2 × 2 matrices, zoals in het dictaat is te zien. Maar ook zonder matrices is gemakkelijk in te zien dat een vermenigvuldiging met
cos φ + i·sin φ
in het complexe vlak beantwoordt aan een rotatie om de oorsprong over een hoek φ.
Fervent tegenstander van het korps lasergamers.
Welk dictaat van complexe functietheorie lees je? Ik heb daar nooit een vak in gevolgd en daar heb ik af en toe last vanquote:
[..]
De inleiding klinkt veelbelovend. Dan ga ik me maar in LinAlg A verdiepen en complexe functietheorie. En ga me niet meer aanbieden, ik ga nu eerst hier m'n tanden inzetten.
.
Riparius stuurde mij dit:quote:
[..]
Welk dictaat van complexe functietheorie lees je? Ik heb daar nooit een vak in gevolgd en daar heb ik af en toe last van
quote:Ik zie dat je kennelijk op zoek bent geweest naar een bewijs van de hoofdstelling van de algebra (elk niet constant polynoom in één variable met complexe coëfficiënten heeft tenminste één nulpunt in C) en dat je daarbij uit was gekomen bij de stelling van Liouville waarvan je het bewijs niet begrijpt. Dat is ook niet zo'n wonder als je niets van complexe functietheorie weet: voor het bewijs van de stelling van Liouville heb je de integraalstelling van Cauchy nodig. Voor de allereerste beginselen van de complexe functietheorie zou je eens kunnen beginnen met dit dictaat:
http://www.staff.science.uu.nl/~ban00101/funcr2012/fr_2012.pdf
Hoofdstuk vier geeft wat hoofdzaken van de complexe functietheorie in kort bestek, inclusief een bewijs van de hoofdstelling van de algebra, maar dan ietsje anders.
Riparius
Fervent tegenstander van het korps lasergamers.
Dat ziet er wel uit als een degelijke basis. Waarom begin je trouwens niet met gewone analyse, of heb je dat al gedaan?quote:
Nope. Momenteel probeer ik verwoed de intro van Money van Pink Floyd te leren op mijn Stratocaster, en dat gaat vrij aardig. Daarnaast probeer ik me te focussen op Lineaire Algebra.quote:
[..]
Dat ziet er wel uit als een degelijke basis. Waarom begin je trouwens niet met gewone analyse, of heb je dat al gedaan?
Fervent tegenstander van het korps lasergamers.
Ok, maar analyse is wel vereiste voorkennis om alles te kunnen snappen. Complexe analyse in Utrecht is dan ook een tweedejaarsvak (en analyse eerstejaars). Dus als je iets met analyse gaat doen, zou ik hiermee beginnen http://www.staff.science.uu.nl/~ban00101/lecnotes/inlan2011.pdf . Daar ben je ook al even zoet mee. Je kan je natuurlijk ook gewoon op lial focussen.quote:
[..]
Nope. Momenteel probeer ik verwoed de intro van Money van Pink Floyd te leren op mijn Stratocaster, en dat gaat vrij aardig. Daarnaast probeer ik me te focussen op Lineaire Algebra.
Shit is getting complicated. Ik start even met Lineaire Algebra.
Fervent tegenstander van het korps lasergamers.
Ik denk dat je niet zomaar moet beginnen met hoofdstuk 4 in het dictaat van Duistermaat, want dan mis je teveel voorkennis. Wat dat betreft is het advies van thenxero om te beginnen met het dictaat Inleiding Analyse van Van den Ban heel terecht. Als je al een goede ondergrond in (reële) analyse hebt zou je toch kunnen beginnen met Duistermaat, maar dan wel met hoofdstuk 1. Het dictaat Lineaire Algebra is inderdaad het eenvoudigst om mee te beginnen, maar voor de beide Analyse dictaten heb je eigenlijk maar heel weinig lineaire algebra nodig.quote:
Shit is getting complicated. Ik start even met Lineaire Algebra.
Daar begin ik dan ook maar mee. Ik kan naderhand ook nog altijd overschakelen op analyse, wat ik denk ik leuker ga vinden.quote:
[..]
Ik denk dat je niet zomaar moet beginnen met hoofdstuk 4 in het dictaat van Duistermaat, want dan mis je teveel voorkennis. Wat dat betreft is het advies van thenxero om te beginnen met het dictaat Inleiding Analyse van Van den Ban heel terecht. Als je al een goede ondergrond in (reële) analyse hebt zou je toch kunnen beginnen met Duistermaat, maar dan wel met hoofdstuk 1. Het dictaat Lineaire Algebra is inderdaad het eenvoudigst om mee te beginnen, maar voor de beide Analyse dictaten heb je eigenlijk maar heel weinig lineaire algebra nodig.
Voor jou persoonlijk heb ik ook nog wat. Ik ga mijn Thorens inwisselen voor een Marlux MX-66. Ook belt-drive, maar wel een volautomaat. Zoals je ongetwijfeld in je geheugen hebt opgeslagen begon het motortje van mijn Thorens wat op leeftijd te raken. Daarnaast is die Marlux gewoon zuivere kwaliteit.
Je hebt nu dus twee soorten draaitafels qua aandrijving, direct en belt-drive. Ik hoor vaak dat de wisselspanning van 50Hz ervoor zorgt dat een direct een minder constant toerental haalt dan een belt-drive. Zit hier een kern van waarheid in?
Fervent tegenstander van het korps lasergamers.
Ja, hoewel je het dictaat Lineaire Algebra van Beukers vast ook wel interessant gaat vinden. Al na het eerste hoofdstuk begrijp je dan wat meer van vectoren, en dat is wel nodig, want ik heb gemerkt dat je daar niet veel van af weet, terwijl dat toch gewoon VWO stof zou moeten zijn. Dan zul je mijn PDF met het bewijs van de additietheorema's voor cos(α + β) en sin(α + β) of bijvoorbeeld deze afleiding van de formules voor het beeldpunt (x'; y') van (x; y) bij een rotatie om de oorsprong ook wel beter begrijpen.quote:
[..]
Daar begin ik dan ook maar mee. Ik kan naderhand ook nog altijd overschakelen op analyse, wat ik denk ik leuker ga vinden.
Ja. Heb je nog wel eens naar een vervangende motor gezocht?quote:Voor jou persoonlijk heb ik ook nog wat. Ik ga mijn Thorens inwisselen voor een Marlux MX-66. Ook belt-drive, maar wel een volautomaat. Zoals je ongetwijfeld in je geheugen hebt opgeslagen begon het motortje van mijn Thorens wat op leeftijd te raken.
Prima ding, maar de arm was ietwat aan de zware kant, dus liever geen elementen met een al te hoge compliantie gebruiken.quote:Daarnaast is die Marlux gewoon zuivere kwaliteit.
Nee, de constantheid van het toerental is het probleem niet, de nauwkeurigheid wordt bepaald door de nauwkeurigheid van de lichtnetfrequentie en die nauwkeurigheid is heel hoog. Maar een elektromotor kan nooit absoluut gelijkmatig (met een constante hoeksnelheid) draaien, en dat heeft een nadelige invloed op de geluidskwaliteit. Bij snaaraandrijving zorgt de massa(traagheid) van het draaiplateau voor een gelijkmatigere rotatie. Een tweede voordeel van snaaraandrijving is de veel betere akoustische ontkoppeling van het draaiplateau ten opzichte van de rest van de draaitafel. Bij een direct aangedreven draaitafel heb je al gauw akoustische terugkoppeling bij weergave via luidsprekers in dezelfde ruimte, en ook dat is nadelig voor de geluidskwaliteit.quote:Je hebt nu dus twee soorten draaitafels qua aandrijving, direct en belt-drive. Ik hoor vaak dat de wisselspanning van 50 Hz ervoor zorgt dat een direct een minder constant toerental haalt dan een belt-drive. Zit hier een kern van waarheid in?
[ Bericht 0% gewijzigd door Riparius op 31-07-2013 18:32:25 ]
Het gewichtDe massa van die arm ervaar ik juist als prettig. De S-arm is veel minder gevoelig dan dat latje in die Thorens. Die kun je eenvoudig zo afstellen dat hij over de plaat vliegt wanneer je een deur opent. De Marlux is ook veel minder gevoelig voor krasjes dus.
En ja, maar die Thorens uit elkaar halen is volgens mij niet eenvoudig. Daarnaast wilde ik toch al tijden die Marlux, dus was het me de moeite niet waard.
[ Bericht 3% gewijzigd door Amoeba op 30-07-2013 04:03:52 ]
En ja, maar die Thorens uit elkaar halen is volgens mij niet eenvoudig. Daarnaast wilde ik toch al tijden die Marlux, dus was het me de moeite niet waard.
[ Bericht 3% gewijzigd door Amoeba op 30-07-2013 04:03:52 ]
Fervent tegenstander van het korps lasergamers.
http://www.marktplaats.nl(...)c624&previousPage=lr
Ik had daarvoor gebeld. Je schrikt wat die schoft ervoor vroeg: 200 euro. In tegenstelling tot het prijskaartje.
Nu had ik er een gevonden inMeijel, vlak langs de deur dus vanaf Deurne, voor 150 minder.
Ik had daarvoor gebeld. Je schrikt wat die schoft ervoor vroeg: 200 euro. In tegenstelling tot het prijskaartje.
Nu had ik er een gevonden inMeijel, vlak langs de deur dus vanaf Deurne, voor 150 minder.
Fervent tegenstander van het korps lasergamers.
(a+b+c)/3 = b + 2((a+c)/2-b)/3 (Pagina 7 http://www.staff.science.uu.nl/~beuke106/linalg/linalg.pdf)
Dit laat zien dat Z op de zwaartelijn door B en de lijn AC ligt. Wanneer we het rechterdeel van de vergelijking beschouwen, merk ik dan juist op dat de term b hier de steunvector aangeeft, en de term 2((a+c)/2-b)/3 hier de richtingsvector? Ik snap alleen even niet hoe ze aan deze richtingsvector komen.
Dit laat zien dat Z op de zwaartelijn door B en de lijn AC ligt. Wanneer we het rechterdeel van de vergelijking beschouwen, merk ik dan juist op dat de term b hier de steunvector aangeeft, en de term 2((a+c)/2-b)/3 hier de richtingsvector? Ik snap alleen even niet hoe ze aan deze richtingsvector komen.
Fervent tegenstander van het korps lasergamers.
Stel je hebt een driehoek met hoekpunten A, B en C. Dan is de a de vector van de oorsprong naar hoekpunt A, b de vector van de oorsprong naar B en c de vector van de oorsprong naar C.quote:
(a+b+c)/3 = b + 2((a+c)/2-b)/3 (Pagina 7 http://www.staff.science.uu.nl/~beuke106/linalg/linalg.pdf)
Dit laat zien dat Z op de zwaartelijn door B en de lijn AC ligt. Wanneer we het rechterdeel van de vergelijking beschouwen, merk ik dan juist op dat de term b hier de steunvector aangeeft, en de term 2((a+c)/2-b)/3 hier de richtingsvector? Ik snap alleen even niet hoe ze aan deze richtingsvector komen.
Als je de zwaartelijn wilt weten van lijnstuk AC door B, dan kun die vinden met twee vectoren:
- De vector vanuit de oorsprong door het punt B
- De vector vanuit de oorsprong door het punt op de helft van lijnstuk AC
De vector vanuit de oorsprong door het punt B hebben we al, namelijk b.
De vector door het punt op de helft van lijnstuk AC kun je vinden door twee vectoren op te tellen: de vector vanuit de oorsprong door punt A en de helft van de verschilvector tussen A en C. De helft van de verschilvector tussen A en C is 1/2 * de vector door C - de vector door A: 1/2(c - a), en de vector door A is a. Dus de vector door het punt op de helft van lijnstuk AC is : a + 1/2(c - a). Dit kun je nog verder uitwerken tot: a + 1/2c - 1/2a = 1/2a + 1/2c = 1/2(a + c).
Nu je de beide vectoren hebt gevonden, vindt je de zwaartelijn als de richtingsvector (de verschilvector van de net twee gevonden vectoren) + de steunvector. Als steun vector hebben we b en als richtingsvector: 1/2(a+c) - b. Dus de zwaartelijn wordt beschreven als:
b + t[1/2(a+c) - b].
Vul je t = 2/3 in dan zul je de zwaartepunt van de driehoek vinden (die dus op de zwaartelijn ligt):
b + 2/3(1/2(a+c) - b) = b + 1/3(a+c) - 2/3b = 1/3b + 1/3(a+c) = 1/3(a+b+c)
Gebruik bij voorkeur vet gedrukte kleine letters om vectoren goed te onderscheiden van bijvoorbeeld scalaire grootheden. Je hebtquote:
(a+b+c)/3 = b + 2((a+c)/2-b)/3 (Pagina 7 http://www.staff.science.uu.nl/~beuke106/linalg/linalg.pdf)
Dit laat zien dat Z op de zwaartelijn door B en de lijn AC ligt. Wanneer we het rechterdeel van de vergelijking beschouwen, merk ik dan juist op dat de term b hier de steunvector aangeeft, en de term 2((a+c)/2-b)/3 hier de richtingsvector? Ik snap alleen even niet hoe ze aan deze richtingsvector komen.
⅓(a + b + c) = b + ⅔(½(a + c) − b)
In een driehoek ABC is de zwaartelijn vanuit hoekpunt B de rechte lijn door punt B en door het midden van zijde AC. Noemen we dit midden van AC even M en vector OM = m, dan kun je gemakkelijk nagaan dat m = ½(a + c). Dit is een direct gevolg van het feit dat de diagonalen van een parallellogram elkaar middendoor delen (maak een tekening). Overigens wordt dit in het dictaat netjes uitgelegd (Lemma 1.2.1).
Aangezien vector OM = m = ½(a + c) en vector OB = b hun eindpunt hebben op de lijn door B en M, dus de zwaartelijn BM, is de verschilvector
OM − OB = m − b = ½(a + c) − b
parallel aan de lijn door B en M en daarmee een richtingsvector voor een vectorvoorstelling van de lijn door B en M. We krijgen dus als vectorvoorstelling voor de zwaartelijn zb vanuit punt B
zb: b + λ(½(a + c) − b)
Voor λ = 0 zitten we in punt B, en voor λ = 1 in het midden van zijde AC. Door permutatie van A, B en C kun je nu gemakkelijk parametervoorstellingen opstellen voor de zwaartelijnen za en zc vanuit punt A resp. punt C. Daarvoor vinden we dan
za: a + λ(½(c + b) − a)
en
zc: c + λ(½(b + a) − c)
Voor λ = ⅔ krijg je nu met alle drie de vectorvoorstellingen de vector ⅓(a + b + c). Dat betekent dus dat het eindpunt van deze vector op alle drie de zwaartelijnen ligt, wat dus impliceert dat de drie zwaartelijnen van een driehoek door één punt gaan. Verder kun je op grond van de waarde λ = ⅔ van de parameter voor dit punt concluderen dat twee zwaartelijnen in een driehoek elkaar verdelen in de verhouding 2 : 1, waarbij het grootste stuk aan de kant van het hoekpunt ligt. Ook dit is een bekende stelling uit de Euclidische meetkunde.
Je kunt nog veel meer bekende stellingen uit de vlakke meetkunde over driehoeken eenvoudig bewijzen met deze vectormethode. Een hele fraaie die niet in het dictaat wordt behandeld maar die ik je niet wil onthouden is de volgende.
Beschouw weer een driehoek ABC en kies het middelpunt O van de omgeschreven cirkel van deze driehoek als oorsprong en neem weer vector OA = a, vector OB = b en vector OC = c. Definieer verder ook een vector h als volgt
h = a + b + c
en noem het eindpunt van deze vector H. Aangezien O het middelpunt is van de omgeschreven cirkel van driehoek ABC, liggen de punten A, B en C op gelijke afstanden van O, zodat de vectoren a, b en c even lang zijn. Het optellingsparallellogram van elk tweetal van deze vectoren is dus een ruit. Maar dit betekent dat de som- en verschilvector van elk tweetal van deze vectoren a, b, en c loodrecht op elkaar staan, omdat immers de diagonalen van een ruit elkaar loodrecht middendoor delen.
We kunnen nu concluderen dat bijvoorbeeld de vector h − c = a + b loodrecht staat op vector a − b. Maar we weten ook dat vector a − b parallel is aan zijde AB van driehoek ABC en dat vector h − c parallel is aan lijnstuk HC. Maar dan staat lijnstuk HC dus loodrecht op zijde AB van driehoek ABC, wat niets anders betekent dan dat punt H op de hoogtelijn vanuit punt C van driehoek ABC ligt. Op dezelfde wijze kun je uiteraard door permutatie van A, B en C aantonen dat punt H eveneens op de hoogtelijnen vanuit punt A en vanuit punt B ligt. En dus heb je zo aangetoond dat de drie hoogtelijnen van een driehoek door één punt gaan en dat is het punt dat we H hadden genoemd.
Maar dit is nog niet alles: eerder zagen we al dat de drie zwaartelijnen van een driehoek door één punt gaan, het zwaartepunt. Noemen we het zwaartepunt Z en de vector OZ = z, dan hebben we gezien dat geldt
z = ⅓(a + b + c)
en dus hebben we nu
z = ⅓h
Maar dit betekent niets anders dan dat het hoogtepunt H, het zwaartepunt Z, en het middelpunt O van de omgeschreven cirkel van een driehoek op één rechte liggen, en wel zó dat HZ : ZO = 2 : 1. Deze rechte wordt de rechte van Euler genoemd.
[ Bericht 0% gewijzigd door Riparius op 30-07-2013 20:14:30 ]
Ik heb ooit bewezen dmv formules van lijnen opstellen dat die punten op de rechte van Euler liggen, dat was een opgave bij wiskunde D. In dat hoofdstuk kregen we vectoren geïntroduceerd als sets getallen. De begrippen richtings- en steunvector waren mij dan ook niet onbekend.
Ah nee, laat maar, ik zie het al.
Het is natuurlijk eenvoudig in te zien dat dat = 2/3 voor iedere vector hetzelfde eindpunt oplevert.
[ Bericht 16% gewijzigd door Amoeba op 30-07-2013 18:17:32 ]
Ah nee, laat maar, ik zie het al.
Het is natuurlijk eenvoudig in te zien dat dat = 2/3 voor iedere vector hetzelfde eindpunt oplevert.
[ Bericht 16% gewijzigd door Amoeba op 30-07-2013 18:17:32 ]
Fervent tegenstander van het korps lasergamers.
Je ziet dat het werken met vectoren an sich voordelen kan hebben boven het werken met vectoren in R2 als geordende paren reële getallen: de formules blijven overzichtelijker en je hebt veel minder rekenwerk.quote:
Ik heb ooit bewezen dmv formules van lijnen opstellen dat die punten op de rechte van Euler liggen, dat was een opgave bij wiskunde D. In dat hoofdstuk kregen we vectoren geïntroduceerd als sets getallen. De begrippen richtings- en steunvector waren mij dan ook niet onbekend.
Dat heb ik wél toegelicht: in elk van de drie vectorvoorstellingen voor de zwaartelijnen za, zb en zc levert de waarde λ = ⅔ de vector ⅓(a + b + c) zodat het eindpunt van deze vector dus op alle drie de zwaartelijnen ligt.quote:Dan rest mij alleen de vraag, niemand licht dat nader toe, waarom = 2/3 het zwaartepunt geeft..
Kan iemand vertellen of ik hier de afgeleide goed bereken?
F(x)= 5 * 3e machtswortel 5x
F'(x)=1/(3* 3e machtswortel x kwadraat)
Mag je uberhaupt die 5 in het begin naar 0 stellen? Ik weet dat als je F(x) = ax + b differentiert je b=0 mag stellen, maar het gaat om hier vermenigvuldigen.
Edit:
Volgens mij moet het zijn:
F'(x)=5/3 3e machtswortel 5x
F(x)= 5 * 3e machtswortel 5x
F'(x)=1/(3* 3e machtswortel x kwadraat)
Mag je uberhaupt die 5 in het begin naar 0 stellen? Ik weet dat als je F(x) = ax + b differentiert je b=0 mag stellen, maar het gaat om hier vermenigvuldigen.
Edit:
Volgens mij moet het zijn:
F'(x)=5/3 3e machtswortel 5x
Nee.quote:
Mag je uberhaupt die 5 in het begin naar 0 stellen? Ik weet dat als je F(x) = ax + b differentiert je b=0 mag stellen, maar het gaat om hier vermenigvuldigen.
Je moet in dit geval de productregel gebruiken:
Stel je hebt f(x) = g(x)*h(x) dan f'(x) = g'(x)*h(x) + g(x)*h'(x)
In dit geval krijg je
f(x) = 5 * 5x^1/3 (je kan een wortel zo schrijven)
g(x) = 5
h(x) = 5x^1/3
Als je de productregel hier toepast, krijg je g'(x) = 0, oftewel de term g'(x)*h(x) = 0
De afgeleide is dus g(x) * h'(x) waarbij h(x) = 5x^1/3
Lukt het vanaf hier verder?
Zie ook http://nl.wikipedia.org/wiki/Productregel_(afgeleide)
Super bedankt Viezze!
Ik krijg nu als eindantwoord: 25 gedeeld door 3 * 3e machtswortel x kwadraat.
Want
h'x=5*1/3 x^-2/3
=5/3 * x^-2/3
= 5/3 * 1/3emachtswortel x kwadraat
= 5/(3 * 3e machtswortel x kwadraat)
* g(x) = 25 gedeeld door (3 * 3e machtswortel x kwadraat)
Is dit correct?
Ik krijg nu als eindantwoord: 25 gedeeld door 3 * 3e machtswortel x kwadraat.
Want
h'x=5*1/3 x^-2/3
=5/3 * x^-2/3
= 5/3 * 1/3emachtswortel x kwadraat
= 5/(3 * 3e machtswortel x kwadraat)
* g(x) = 25 gedeeld door (3 * 3e machtswortel x kwadraat)
Is dit correct?
Nee, dit is niet goed, en ik zie ook niet hoe je hierbij komt. Dat mag je me eens haarfijn uitleggen, want ik ben altijd geïnteresseerd in dat soort kromme gedachten.quote:
Kan iemand vertellen of ik hier de afgeleide goed bereken?
F(x)= 5 * 3e machtswortel 5x
F'(x)=1/(3* 3e machtswortel x kwadraat)
Gebruik trouwens superscript voor exponenten en worteltekens, dit is wel erg moeizaam leesbaar en werkt mede daardoor fouten en onbegrip in de hand.
Dit geeft al aan dat je totaal niet begrijpt wat differentiëren inhoudt. Er is geen sprake van dat je iets zomaar gelijk aan nul mag stellen. Ook constanten niet. De afgeleide van een constante is weliswaar nul, maar dat betekent helemaal niet dat je die constante door nul vervangt.quote:Mag je uberhaupt die 5 in het begin naar 0 stellen? Ik weet dat als je F(x) = ax + b differentieert je b=0 mag stellen, maar het gaat om hier vermenigvuldigen.
Nee.quote:Edit:
Volgens mij moet het zijn:
F'(x)=5/3 3e machtswortel 5x
Welk boek gebruik je eigenlijk? Een tijdje geleden had ik je dit boek aangeraden omdat je zei je voor te willen bereiden op de Vlaamse toelatingsexamens, maar uit dit boek zul je bovenstaande rare ideeën over differentiëren toch wel niet hebben opgepikt ...
Ik snap niet echt wat je hier doet, het zou handiger zijn als jequote:
Super bedankt Viezze!
Ik krijg nu als eindantwoord: 25 gedeeld door 3 * 3e machtswortel x kwadraat.
Want
h'x=5*1/3 x^-2/3
=5/3 * x^-2/3
= 5/3 * 1/3emachtswortel x kwadraat
= 5/(3 * 3e machtswortel x kwadraat)
* g(x) = 25 gedeeld door (3 * 3e machtswortel x kwadraat)
Is dit correct?
dit advies opvolgtquote:
Gebruik trouwens superscript voor exponenten en worteltekens, dit is wel erg moeizaam leesbaar en werkt mede daardoor fouten en onbegrip in de hand.
Hoe ik daar bij ben gekomen? Door van iets uit te gaan wat niet klopt. Ik dacht namelijk dat je de 5 in mijn eerste functie aan 0 kon stellen. Toen ben ik dus op dat antwoord gekomen.quote:
[..]
Nee, dit is niet goed, en ik zie ook niet hoe je hierbij komt. Dat mag je me eens haarfijn uitleggen, want ik ben altijd geïnteresseerd in dat soort kromme gedachten.
Gebruik trouwens superscript voor exponenten en worteltekens, dit is wel erg moeizaam leesbaar en werkt mede daardoor fouten en onbegrip in de hand.
[..]
Dit geeft al aan dat je totaal niet begrijpt wat differentiëren inhoudt. Er is geen sprake van dat je iets zomaar gelijk aan nul mag stellen. Ook constanten niet. De afgeleide van een constante is weliswaar nul, maar dat betekent helemaal niet dat je die constante door nul vervangt.
[..]
Nee.
Welk boek gebruik je eigenlijk? Een tijdje geleden had ik je dit boek aangeraden omdat je zei je voor te willen bereiden op de Vlaamse toelatingsexamens, maar uit dit boek zul je bovenstaande rare ideeën over differentiëren toch wel niet hebben opgepikt ...
Ik twijfelde eerst of ik uberhaupt de productregel mocht toepassen, want ik dacht, 'he, dan is f'(x)=0, en dat kan niet' en toen heb ik niet meer gedacht aan de productregel. Totdat Viezze het had uitgelegd en ik weer verder kon.
Trouwens, dat boek heb ik gister binnengehad. En ik heb nog niet uit het boek geleerd, maar vandaag voor het eerst langs mijn toekomstige wiskunde docent gegaan die mijn wiskunde a kennis deels naar boven haalde en daarbij ook wiskunde b stof uitgelegd had; heel leuk.
Nee. Stop je functie gewoon even in WolframAlpha, dat bespaart een hoop nutteloze posts met verkeerde antwoorden.quote:
Ik krijg nu als eindantwoord: 25 gedeeld door 3 * 3e machtswortel x kwadraat.
Is dit correct?
Dit bedoelde ik trouwens:
http://i39.tinypic.com/14mt79c.jpg
Maar volgens wolframalpha klopt het niet, dus ik zal weer opnieuw beginnen.
Ik zal superscript bekijken trouwens, dankje.
http://i39.tinypic.com/14mt79c.jpg
Maar volgens wolframalpha klopt het niet, dus ik zal weer opnieuw beginnen.
Ik zal superscript bekijken trouwens, dankje.
Je hebt de productregel of de kettingregel hier helemaal niet nodig. Je hebt namelijkquote:
[..]
Ik twijfelde eerst of ik uberhaupt de productregel mocht toepassen, want ik dacht, 'he, dan is f'(x)=0, en dat kan niet' en toen heb ik niet meer gedacht aan de productregel. Totdat Viezze het had uitgelegd en ik weer verder kon.
5·∛(5x) = 5·∛5·x1/3
Die 5·∛5 is een constante, en aangezien d(c·f(x))/dx = c·d(f(x))/dx hoef je dus alleen nog te weten hoe je x1/3 differentieert, en dat gaat via de bekende regel
d(xn)/dx = n·xn−1
die ook voor gebroken waarden van n geldt.
Net nog alles nagelopen en ik kom op het antwoord van wolframalpha uit.
[ Bericht 8% gewijzigd door DefinitionX op 31-07-2013 22:44:25 ]
[ Bericht 8% gewijzigd door DefinitionX op 31-07-2013 22:44:25 ]
Waarom zegt Wolframalpha: http://www.wolframalpha.com/input/?i=derive+root%283x-4%29
En mijn boek wat anders voor de regel van de afgeleide van een wortel x?
Want m.b.v. boekregel heb ik dit gekregen, maar wolframalpha zegt wat anders over het differentieren van de wortel.
http://i44.tinypic.com/k2labo.jpg
http://i44.tinypic.com/1z6h1s2.jpg
Kan iemand dit alsjeblieft nader toelichten? Het gaat erom dat voor d'(x) wolframalpha wat anders zegt.
En mijn boek wat anders voor de regel van de afgeleide van een wortel x?
Want m.b.v. boekregel heb ik dit gekregen, maar wolframalpha zegt wat anders over het differentieren van de wortel.
http://i44.tinypic.com/k2labo.jpg
http://i44.tinypic.com/1z6h1s2.jpg
Kan iemand dit alsjeblieft nader toelichten? Het gaat erom dat voor d'(x) wolframalpha wat anders zegt.
http://www.wisfaq.nl/pagina.asp?nummer=1459
Zie voorbeeld twee en het antwoord op deze vraag:
http://www.goeievraag.nl/(...)-wortel-5x-11.195718
Zelf wat in Google intypen is niet strafbaar hoor
Zie voorbeeld twee en het antwoord op deze vraag:
http://www.goeievraag.nl/(...)-wortel-5x-11.195718
Zelf wat in Google intypen is niet strafbaar hoor
Ik heb ook gegoogled, maar niets gevonden.
Nu heb ik de regel, maar ik weet niet waarom het zo is.
Thanks btw.
Nu heb ik de regel, maar ik weet niet waarom het zo is.
Thanks btw.
Ga nu eerst maar eens dat boek goed bestuderen, dan krijg je een beter beeld dan zo maar hap snap wat opgaven proberen waar je nog niet aan toe bent.quote:
Ik heb ook gegoogled, maar niets gevonden.
Nu heb ik de regel, maar ik weet niet waarom het zo is.
Thanks btw.
d((3x − 4)1/2)/dx = d((3x − 4)1/2)/d(3x − 4) · d(3x − 4)/dx = ½·(3x − 4)−1/2·3 = 3/(2√(3x − 4)).
Complexe analyse in Utrecht is juist een derdejaarsvakquote:
[..]
Ok, maar analyse is wel vereiste voorkennis om alles te kunnen snappen. Complexe analyse in Utrecht is dan ook een tweedejaarsvak (en analyse eerstejaars). Dus als je iets met analyse gaat doen, zou ik hiermee beginnen http://www.staff.science.uu.nl/~ban00101/lecnotes/inlan2011.pdf . Daar ben je ook al even zoet mee. Je kan je natuurlijk ook gewoon op lial focussen.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Nog ergerquote:
[..]
Complexe analyse in Utrecht is juist een derdejaarsvak
Gewoon eerst met lineare algebra van Beukers beginnenquote:
Shit is getting complicated. Ik start even met Lineaire Algebra.
en daarna pas met inleidend analyse van van den Ban.
Croce e delizia cor. Misterioso, Misterioso altero, croce e delizia al cor.
Ik heb een vraag over de euclidische deling.
In mijn boek staat dit:
Ik snap alleen niet hoe ze aan de getallen links komen komen (dus 625, 285, 207).
Dit is hoe ik het doe:
Ik zet dan links wat er overblijft als je het origineel vermindert met veelvoud van rechts.
Kan iemand aub uitleggen wat het boek bedoelt? Ik krijg geloof ik wel steeds het goede antwoord.
In mijn boek staat dit:
Ik snap alleen niet hoe ze aan de getallen links komen komen (dus 625, 285, 207).
Dit is hoe ik het doe:
Ik zet dan links wat er overblijft als je het origineel vermindert met veelvoud van rechts.
Kan iemand aub uitleggen wat het boek bedoelt? Ik krijg geloof ik wel steeds het goede antwoord.
Wacht....Ik zie het geloof ik. Ze vermenigvuldigen steeds eerst 3 met 2, met 0 en dan weer 7, zo krijg je 621. Dan doen ze dat met 1 en krijg je 207 en dan weer met 3 en dan krijg je 621. Ik vind de notatie zelf een beetje verwarrend.
3 = -621
1 = -207
3 = -621
Echter, hoe zijn ze dan aan het rekenen?
3 = -621
1 = -207
3 = -621
Echter, hoe zijn ze dan aan het rekenen?
Zoals het boek al zegt, ze voeren een staartdeling uit. Dit werd eeuwenlang gewoon geleerd op de lagere school en in de rest van de beschaafde wereld gebeurt dat nog steeds, alleen in Nederland niet. Kijk even in Wikipedia voor uitleg.quote:
Wacht....Ik zie het geloof ik. Ze vermenigvuldigen steeds eerst 3 met 2, met 0 en dan weer 7, zo krijg je 621. Dan doen ze dat met 1 en krijg je 207 en dan weer met 3 en dan krijg je 621. Ik vind de notatie zelf een beetje verwarrend.
3 = -621
1 = -207
3 = -621
Echter, hoe zijn ze dan aan het rekenen?
Ik zal er naar kijken!quote:
[..]
Zoals het boek al zegt, ze voeren een staartdeling uit. Dit werd eeuwenlang gewoon geleerd op de lagere school en in de rest van de beschaafde wereld gebeurt dat nog steeds, alleen in Nederland niet. Kijk even in Wikipedia voor uitleg.
Echter, ik snap al (deels) wat het boek aan het doen is. In de staartdeling in het voorbeeld laten ze getallen weg, en die getallen moet je erbij fantaseren op de lege plekken in het voorbeeld.
Trouwens, lol over wat je zegt over 'rest van de beschaafde wereld'. Hehe.
Nou nee hoor, ze laten niets weg bij de uitwerking en je moet er ook niets bij fantaseren, zo werkt rekenkunde niet.quote:
[..]
Ik zal er naar kijken!
Echter, ik snap al (deels) wat het boek aan het doen is. In de staartdeling in het voorbeeld laten ze getallen weg, en die getallen moet je erbij fantaseren op de lege plekken in het voorbeeld.
Als het de bedoeling is 64953 te delen door 207 dan begin je met de eerste drie cijfers 649 van het deeltal, aangezien 64 < 207 en 649 > 207. We zien dan dat 207 driemaal in 649 zit, want 3·207 = 621. Dus noteren we (in de Vlaamse manier van opschrijven) rechts onder het deeltal een 3 en noteren we die 621 onder 649. Aftrekken geeft dan 649 − 621 = 28. Dit is uiteraard kleiner dan 207. Nu halen we het volgende cijfer van het deeltal erbij, dat is de 5, zodat we 285 krijgen en dat is weer groter dan 207. Dit wordt wel het aanhalen van het volgende cijfer genoemd. Soms zie je dit ook uitgebeeld met een verticale stippellijn vanaf het betreffende cijfer in het deeltal. Nu werk je weer op dezelfde wijze als eerder met dat getal 649: we zien dat 207 éénmaal in 285 zit, dus noteren we rechts naast de 3 die we eerder hadden opgeschreven een 1 en zetten we 207 onder 285. Aftrekken geeft dan 78. Tenslotte halen we de 3 aan, dit is het laatste cijfer van het deeltal, en dan hebben we 783. Nu zien we dat 207 weer 3 maal in 783 past, dus noteren we rechts naast de 3 en de 1 die er al staan nog een 3 en zetten we weer 3·207 = 621 onder de 783. Aftrekken geeft dan tenslotte 783 − 621 = 162. Nu kunnen we niet verder en is de staartdeling voltooid.
Het quotiënt van 64953 en 207 is dus 313 met een rest 162, oftewel 64953 = 313·207 + 162.
Uiteraard is het ook mogelijk dat er geen rest is en dat de staartdeling dus uitkomt op 0. Dan zegt men gewoonlijk kortweg dat de staartdeling uitkomt.
Het is niet grappig meer als je weet hoe waar het is.quote:Trouwens, lol over wat je zegt over 'rest van de beschaafde wereld'. Hehe.
Oudere onderwijzer waarschijnlijk die zich geen moer aantrok van wat hij volgens het boekje moest onderwijzen. En bedenk dat de stagiaires van vandaag de onderwijzers en onderwijzeressen van morgen zijn. Zie ook hier.quote:
Ik kreeg op de basisschool gewoon staartdelingen hoor. Alleen de stagiaires konden het niet
Mijn leraren waren inderdaad bijna met pensioen. Ik realiseer me ook dat die stagiaires helaas een afspiegeling vormen van het niveau van nu.
Op zich valt er ook best wel wat te zeggen voor het "moderne" rekenen. Hoofdrekenen is immers grotendeels "moderne" rekenentechnieken toepassen. Het probleem is denk ik vooral dat er geen solide basis wordt opgebouwd (waaronder dus staartdelingen).
Als ik 43050/350 uit mijn hoofd wil doen, dan doe ik in feite ook "repeterend aftrekken". Eerst 100×350 = 35 000 eraftrekken, dan heb je nog 8050 over. Nog 20×350 eraf, dus nog 1050=3×350 over. Dus 100+20+3 = 123 is het antwoord. Prima als je de kids laat inzien dat je op die manier ook een beetje creatief kan rekenen.
Op zich valt er ook best wel wat te zeggen voor het "moderne" rekenen. Hoofdrekenen is immers grotendeels "moderne" rekenentechnieken toepassen. Het probleem is denk ik vooral dat er geen solide basis wordt opgebouwd (waaronder dus staartdelingen).
Als ik 43050/350 uit mijn hoofd wil doen, dan doe ik in feite ook "repeterend aftrekken". Eerst 100×350 = 35 000 eraftrekken, dan heb je nog 8050 over. Nog 20×350 eraf, dus nog 1050=3×350 over. Dus 100+20+3 = 123 is het antwoord. Prima als je de kids laat inzien dat je op die manier ook een beetje creatief kan rekenen.
Riparius, heb je ooit een parttime functie als onderwijzer overwogen? Je zou niet de enige zijn, zelfs onze premier staat nog voor de klas.
Fervent tegenstander van het korps lasergamers.
Ik heb het juist dat Rn ook een n-dimensionale vectorruimte vertegenwoordigd?
Fervent tegenstander van het korps lasergamers.
Ja, want R^n kan worden opgebouwd uit n orthogonale eenheidsvectoren van lengte n.quote:
Ik heb het juist dat Rn ook een n-dimensionale vectorruimte vertegenwoordigd?
WEB / [HaxBall #64] Jos is God
Arguing on the Internet is like running in the Special Olympics.
Arguing on the Internet is like running in the Special Olympics.
Rn is zelf strikt genomen nog geen vectorruimte. Pas als je optelling en vermenigvuldiging met een scalair definieert voor de elementen van Rn, op zo'n manier dat er aan een aantal axioma's is voldaan.quote:
Ik heb het juist dat Rn ook een n-dimensionale vectorruimte vertegenwoordigd?
Zie http://nl.wikipedia.org/wiki/Vectorruimte .
Rn staat voor R×R×...×R (n keer), i.e. het Carthesische product van n keer een R. Dus x is een element van Rn dan en slechts dan als x=(x1,x2,...,xn), waarbij alle xi in R zitten.
Kan iemand controleren of het bovenstaande klopt? Wolframalpha zegt iets anders, maar ik denk dat w-alpha het aan het vereenvoudigen is, wat mij niet lukt.
Ik kan nauwelijks lezen wat je opschrijft, je zult toch iets duidelijker moeten schrijven. En gebruik geen hoofdletter F voor een functie f, aangezien F meestal wordt gebruikt om een primitieve van f aan te duiden.quote:
[ afbeelding ]
Kan iemand controleren of het bovenstaande klopt? Wolframalpha zegt iets anders, maar ik denk dat w-alpha het aan het vereenvoudigen is, wat mij niet lukt.
Bedoel je nu
f(x) = 6·4√(6x)
?
Ja dat bedoel ik. Ik ga proberen netter te schrijven en opnieuw te posten.quote:
[..]
Ik kan nauwelijks lezen wat je opschrijft, je zult toch iets duidelijker moeten schrijven. En gebruik geen hoofdletter F voor een functie f, aangezien F meestal wordt gebruikt om een primitieve van f aan te duiden.
Bedoel je nu
f(x) = 6·4√(6x)
?
Goed. Ik zie dat je in de veronderstelling verkeert dat je de productregel moet gebruiken om de afgeleide van f(x) te bepalen, maar dat is niet zo. Je kunt hier twee rekenregels gebruiken. Om te beginnen is een wortel uit een product gelijk aan het product van de wortels van de factoren van dat product, mits deze factoren niet negatief zijn. Dus hebben we hierquote:
[..]
Ja dat bedoel ik. Ik ga proberen netter te schrijven en opnieuw te posten.
4√(6x) = 4√6·4√x
Ten tweede is het nemen van de n-de machts wortel uit een (niet negatief) getal equivalent met het verheffen van dat getal tot de macht 1/n. Dus hebben we hier
4√x = x1/4
We kunnen zo dus schrijven
f(x) = 6·4√6·x1/4
Hier is 6·4√6 een constante, zodat we nu gebruik kunnen maken van de regels
d(c·f(x))/dx = c·d(f(x))/dx
en
d(xn)/dx = n·xn−1
om de afgeleide te bepalen van f(x). En dus krijgen we
f'(x) = 6·4√6·(1/4)·x−3/4
Als je de afgeleide weer met behulp van wortels wil schrijven, dan kun je dit nog herleiden door gebruik te maken van x−3/4 = 1/x3/4 = 1/(x3)1/4 = 1 / 4√(x3) en dan krijgen we dus
f'(x) = 6·4√6 / (4·4√(x3))
oftewel
f'(x) = 3·4√6 / (2·4√(x3))
[ Bericht 1% gewijzigd door Riparius op 03-08-2013 20:34:28 ]
Ga ook eens proberen op te letten?quote:
[..]
Ja dat bedoel ik. Ik ga proberen netter te schrijven en opnieuw te posten.
Wat Riparius hierboven vertelt heeft hij een paar dagen geleden als eens eerder uitgelegd, om precies te zijn hier:
Uitgaande van bovenstaande constateer ik dus dat ditquote:
[..]
Je hebt de productregel of de kettingregel hier helemaal niet nodig. Je hebt namelijk
5·∛(5x) = 5·∛5·x1/3
Die 5·∛5 is een constante, en aangezien d(c·f(x))/dx = c·d(f(x))/dx hoef je dus alleen nog te weten hoe je x1/3 differentieert, en dat gaat via de bekende regel
d(xn)/dx = n·xn−1
die ook voor gebroken waarden van n geldt.
een beetje overdreven is.quote:
Riparius, je bent een harde, maar ik snap het nu wel!
Uber uber bedankt!
Fervent tegenstander van het korps lasergamers.
Riparius, ik dank u.
Dude, dat ik het niet meteen snap betekent nog niet dat ik niet aan het opletten ben. Ik zie het gewoon niet meteen zo goed als jij en andere......Ik heb nooit gezegd dat ik goed ben in wiskunde, maar ik sta open om te leren.quote:
[..]
Ga ook eens proberen op te letten?
Wat Riparius hierboven vertelt heeft hij een paar dagen geleden als eens eerder uitgelegd, om precies te zijn hier:
[..]
Uitgaande van bovenstaande constateer ik dus dat dit
[..]
een beetje overdreven is.
Yes sir.quote:
[..]
Zie je nu ook hoe je mijn uitkomst kunt herleiden tot de uitkomst die WolframAlpha geeft?
Alleen, kun jij misschien uitleggen hoe w-alpha het antwoord vereenvoudigt?
http://www.wolframalpha.com/input/?i=derive+6*%286x%29^1%2F4
Edit:
Ik bedoelde nee.....
edit: verkeerde topic
WEB / [HaxBall #64] Jos is God
Arguing on the Internet is like running in the Special Olympics.
Arguing on the Internet is like running in the Special Olympics.
Ik zag al dat je jezelf tegensprak.quote:
[..]
Yes sir.
Alleen, kun jij misschien uitleggen hoe w-alpha het antwoord vereenvoudigt?
http://www.wolframalpha.com/input/?i=derive+6*%286x%29^1%2F4
Edit:
Ik bedoelde nee.....
We waren gekomen tot
f'(x) = 3·4√6 / (2·4√(x3))
In de teller van dit quotiënt hebben we een factor
4√6
waarvoor we volgens de rekenregels voor wortels kunnen schrijven
4√2·4√3
en dus ook
21/4·4√3
Nu zie je in de noemer van het quotiënt van de afgeleide een factor 2 staan, en dit is eigenlijk 21, waarvoor we ook kunnen schrijven
23/4·21/4
Dus hebben we
f'(x) = (3·21/4·4√3) / (23/4·21/4·4√(x3))
Nu zie je dat teller en noemer van de breuk een factor 21/4 gemeen hebben, zodat we teller en noemer van de breuk door 21/4 kunnen delen, en dit geeft
f'(x) = (3·4√3) / (23/4·4√(x3))
oftewel
f'(x) = (3·4√3) / (23/4·x3/4)
en dat is precies wat WolframAlpha ook geeft.
Dit soort algebraïsche herleidingen met (bijvoorbeeld) wortels en exponenten moet je volledig beheersen, anders kun je jezelf echt de moeite besparen ooit deel te nemen aan die toelatingstoets.
[ Bericht 1% gewijzigd door Riparius op 03-08-2013 22:19:27 ]
Ik zag op het laatste moment, voor je post dus, wat ze deden met het splitsen van de wortels (waarschijnlijk verkeerde benaming), maar wat je deed met die 2, dat is nieuw voor mij. Ik weet dat 2^3/4·2^1/4 = 2, maar dat je het op die manier kon gebruiken niet. Weer wat geleerd.
Trouwens, bedankt dat je zoveel geduld hebt met me, en dat geldt voor iedereen op het fok beta. Kijk, ik kan nu opgeven en dan zeggen 'ja het was te moeilijk, ga ik toch niet snappen', maar dat is de verkeerde mentaliteit.
Ik had laatst een gedachte: wat als ik ipv wiskunde als een blok zie dat ik verder moet duwen om te komen waar ik wil, het ga behandelen als iets dat me mentaal helpt en ook in de toekomst zeer van pas gaat komen.
Nu zit ik niet meer met 'x uur per dag beta', maar meer 'dit leren is behalve voor die toets gewoon interessant om te weten'. Met zo'n houding gaat het ook veel makkelijker en is het bovendien leuker.
Genoeg gekletst, de boeken weer in. :p
Trouwens, bedankt dat je zoveel geduld hebt met me, en dat geldt voor iedereen op het fok beta. Kijk, ik kan nu opgeven en dan zeggen 'ja het was te moeilijk, ga ik toch niet snappen', maar dat is de verkeerde mentaliteit.
Ik had laatst een gedachte: wat als ik ipv wiskunde als een blok zie dat ik verder moet duwen om te komen waar ik wil, het ga behandelen als iets dat me mentaal helpt en ook in de toekomst zeer van pas gaat komen.
Nu zit ik niet meer met 'x uur per dag beta', maar meer 'dit leren is behalve voor die toets gewoon interessant om te weten'. Met zo'n houding gaat het ook veel makkelijker en is het bovendien leuker.
Genoeg gekletst, de boeken weer in. :p
Het is niet expliciet wortels splitsen.quote:
Ik zag op het laatste moment, voor je post dus, wat ze deden met het splitsen van de wortels (waarschijnlijk verkeerde benaming), maar wat je deed met die 2, dat is nieuw voor mij. Ik weet dat 2^3/4·2^1/4 = 2, maar dat je het op die manier kon gebruiken niet. Weer wat geleerd.
Trouwens, bedankt dat je zoveel geduld hebt met me, en dat geldt voor iedereen op het fok beta. Kijk, ik kan nu opgeven en dan zeggen 'ja het was te moeilijk, ga ik toch niet snappen', maar dat is de verkeerde mentaliteit.
Ik had laatst een gedachte: wat als ik ipv wiskunde als een blok zie dat ik verder moet duwen om te komen waar ik wil, het ga behandelen als iets dat me mentaal helpt en ook in de toekomst zeer van pas gaat komen.
Nu zit ik niet meer met 'x uur per dag beta', maar meer 'dit leren is behalve voor die toets gewoon interessant om te weten'. Met zo'n houding gaat het ook veel makkelijker en is het bovendien leuker.
Genoeg gekletst, de boeken weer in. :p
Stel je hebt:
an
Stel nu dat a = b·c
Substitutie levert op:
(b·c)n
En dit is waar ik naartoe wilde, een rekenregel voor machten is dat:
(b·c)n = bn·cn
Daar worteltrekken in feite niets anders is dan populaire taal voor machtsverheffen met n = 1/2 geldt dat uiteraard ook zodat je zonder moeite kunt zeggen dat:
√6 = √(3·2) = √3 · √2
Edit:
Ik zie nu wat je bedoelt..
Dat is weer gebruik maken van een andere rekenregel voor machten.
Fervent tegenstander van het korps lasergamers.
Vanaf 1:46
In de eerste opgave die hij behandelt neemt hij de logaritme van wat er links staat en wat er rechts staat (vanaf tijdstip 1:46 zie je dat), maar ik heb alles wat links en rechts staat een exponent gemaakt van 10. Zo krijg ik hetzelfde antwoord. Kan het allebei?
Een logaritme is in feite een exponent, want glog a is gedefinieerd als de exponent waartoe je het grondtal g moet verheffen om a te krijgen. Dusquote:
Vanaf 1:46
In de eerste opgave die hij behandelt neemt hij de logaritme van wat er links staat en wat er rechts staat (vanaf tijdstip 1:46 zie je dat), maar ik heb alles wat links en rechts staat een exponent gemaakt van 10. Zo krijg ik hetzelfde antwoord. Kan het allebei?
glog a = b
is equivalent met
gb = a
Je vraag is verder niet duidelijk genoeg, want ik kan uit je beschrijving niet opmaken of je het correct opschrijft. Dat zul je dus eerst moeten laten zien.
Als we hebben
10log(S4/R2) = 1
dan is dit conform de definitie van de logaritme equivalent met
101 = S4/R2
en dus
S4 = 10·R2
De man in de video herschrijft eerst 1 als 10log 10 en maakt dan gebruik van het feit dat
glog a = glog b
equivalent is met
a = b
mits a en b beide positieve grootheden zijn.
Dit is wat ik gedaan heb:quote:
[..]
Een logaritme is in feite een exponent, want glog a is gedefinieerd als de exponent waartoe je het grondtal g moet verheffen om a te krijgen. Dus
glog a = b
is equivalent met
gb = a
Je vraag is verder niet duidelijk genoeg, want ik kan uit je beschrijving niet opmaken of je het correct opschrijft. Dat zul je dus eerst moeten laten zien.
Als we hebben
10log(S4/R2) = 1
dan is dit conform de definitie van de logaritme equivalent met
101 = S4/R2
en dus
S4 = 10·R2
De man in de video herschrijft eerst 1 als 10log 10 en maakt dan gebruik van het feit dat
glog a = glog b
equivalent is met
a = b
mits a en b beide positieve grootheden zijn.
Is dat ook correct? Ik hoop dat het duidelijk geschreven is.
Edit:
Eigenlijk zie ik nu wel wat die man heeft gedaan, mede door jouw uitleg. 10^log10 is 10^1 en dat is weer 10. Dankjewel.
Edit2: Nee klopt niet, 10^log10 = 1. Ik doelde op de exponent.
Edit3: Ik schrijf de S^4 op het laatst verkeerd in de foto....
[ Bericht 2% gewijzigd door DefinitionX op 04-08-2013 22:46:18 ]
Wat je hier doet is correct, afgezien van de verschrijving S4 voor S4.quote:
[..]
Dit is wat ik gedaan heb:
[ afbeelding ]
Is dat ook correct? Ik hoop dat het duidelijk geschreven is.
Eerst maak je hier gebruik van het feit dat
a = b
equivalent is met
10a = 10b
Vervolgens gebruik je dat
10log(a) = a
waarbij log staat voor de 'gewone' oftewel Briggse logaritmen met grondtal 10. Deze laatste regel is weer niets anders dan de definitie van de logaritme: log(a) is de exponent waartoe je 10 moet verheffen om a te krijgen.
Wees er bedacht op dat er wat ambiguïteit in notaties van logaritmen bestaat. In veel toegepaste disciplines (en bijvoorbeeld op rekenmachines) wordt met log de logaritme met grondtal 10 bedoeld, maar in de zuivere wiskunde wordt log dan weer vaak gebruikt om logaritmen met grondtal e (het getal van Euler) aan te geven. Deze laatste logaritmen heten ook natuurlijke logaritmen en worden om misverstanden te voorkomen (en op rekenmachines) ook vaak aangegeven met het symbool ln (dat staat voor logarithmus naturalis).
WolframAlpha interpreteert zowel log als ln als de natuurlijke logaritme. Als je bij WolframAlpha een ander grondtal g wil gebruiken, dan moet je dat specificeren. glog a voer je dan in als log(g, a).
Hoi, ik heb een beetje aparte vraag. Ik probeer deze vraag op te lossen:
[ Bericht 1% gewijzigd door randomo op 09-08-2013 21:05:30 ]
En ik weet (met dank aan Riparius) dat het antwoord hier staat (vraag A2), maar ik wil liever niet het antwoord bekijken. Ik weet niet of het mogelijk is, maar zou iemand me een tip kunnen geven?quote:For what pairs (a, b) of positive real numbers does the improper integral
converge?
[ Bericht 1% gewijzigd door randomo op 09-08-2013 21:05:30 ]
Probeer eens eerste orde Taylorbenaderingen te gebruiken vanquote:
Hoi, ik heb een beetje aparte vraag. Ik probeer deze vraag op te lossen:
[..]
En ik weet (met dank aan Riparius) dat het antwoord hier staat (vraag A2), maar ik wil liever niet het antwoord bekijken. Ik weet niet of het mogelijk is, maar zou iemand me een tip kunnen geven?
Thanks, ik kijk vanavond nog even, ik laat nog wel even weten of ik er uitgekomen ben (of denk er uitgekomen te zijn, ik trek soms nog wel eens te snel conclusies )
)
Je zult er wel meer dan even over na moeten denkenquote:
Thanks, ik kijk vanavond nog even, ik laat nog wel even weten of ik er uitgekomen ben (of denk er uitgekomen te zijn, ik trek soms nog wel eens te snel conclusies
Ja. Ik bedacht net dat ik er echt nog geen zak van begrijp, ik heb geen idee hoe te beginnenquote:
[..]
Je zult er wel meer dan even over na moeten denken
Dat heb ik wel vaker bij die calculus problemen, daar heb ik ook niet veel ervaring mee, lastig lastig...
Heb je al geprobeerd die wortels te rationaliseren? Dit riekt aan alle kanten naar een probleem dat met worteltruuk
√a + √b = (√a + √b)*(√a - √b)/(√a - √b) opgelost dient te worden.
[ Bericht 1% gewijzigd door VanishedEntity op 09-08-2013 02:30:34 ]
√a + √b = (√a + √b)*(√a - √b)/(√a - √b) opgelost dient te worden.
[ Bericht 1% gewijzigd door VanishedEntity op 09-08-2013 02:30:34 ]
Je zou kunnen beginnen met de opgave correct weer te geven. Je hebt de integratiegrenzen vergeten aan te geven. Het is de bedoeling te integreren over [b, ∞).quote:
Hoi, ik heb een beetje aparte vraag. Ik probeer deze vraag op te lossen:
[..]
En ik weet (met dank aan Riparius) dat het antwoord hier staat (vraag A2), maar ik wil liever niet het antwoord bekijken. Ik weet niet of het mogelijk is, maar zou iemand me een tip kunnen geven?
Verder vraag ik me af waarom je zo graag tips wil hebben, het is toch de bedoeling om de Putnam opgaven zelf op te lossen. Als je een opgave alleen met tips van anderen op kunt lossen, dan kun je achteraf niet zeggen dat je zelf een oplossing hebt gevonden, want dan houd je alleen maar jezelf voor de gek.
[ Bericht 6% gewijzigd door Riparius op 09-08-2013 18:07:28 ]
Haha, een echte Riparius-reactie. Je hebt gelijk ja, excuses van de integraal (hoewel je zou kunnen zeggen dat de integraal genomen moet worden over het domein waar de integrand 'geldig is', maar goed, dat is dan meer bij toeval, en je zou dan ook een complexe integraal kunnen bedoelen...).quote:
[..]
Je zou kunnen beginnen met de opgave correct weer te geven. Je hebt de integratiegrenzen vergeten aan te geven. Het is de bedoeling te integreren over [b, ∞).
Verder vraag ik me af waarom je zo graag tips wil hebben, het is toch de bedoeling om de Putnam opgaven zelf op te lossen. Als een opgave alleen met tips van anderen op kunt lossen, dan kun je achteraf niet zeggen dat je zelf een oplossing hebt gevonden, want dan houd je alleen maar jezelf voor de gek.
Ik moet zeggen dat ik sowieso de hoop al heb opgegeven om deze nog te op te lossen, maar gelijk naar de antwoorden kijken vind ik ook weer zoiets
Ik kan het blijkbaar moeilijk verkroppen dat ik de opgave niet op kan lossen (vooral ook omdat het A2 is, en meestal zijn de eerste opgaven juist vrij makkelijk).
Als je het hebt over een oneigenlijke integraal, dan is dat een definiete integraal en dan moet je dus de integratiegrenzen aangeven.quote:
[..]
Haha, een echte Riparius-reactie. Je hebt gelijk ja, excuses van de integraal (hoewel je zou kunnen zeggen dat de integraal genomen moet worden over het domein waar de integrand 'geldig is', maar goed, dat is dan meer bij toeval, en je zou dan ook een complexe integraal kunnen bedoelen...).
Tja, de vraag is wat voor tips je eigenlijk verwacht als je een uitgewerkte oplossing er al meteen bij geeft. Je wil niet zelf naar de uitwerking kijken maar kennelijk wel dat iemand je al een stukje van de uitwerking waar je zelf niet naar wil kijken verklapt. Dat is hypocriet.quote:Ik moet zeggen dat ik sowieso de hoop al heb opgegeven om deze nog te op te lossen, maar gelijk naar de antwoorden kijken vind ik ook weer zoiets
Interessanter zijn dan tips voor alternatieve oplossingen. Je kunt gemakkelijk laten zien dat de integrand voor x → ∞ asymptotisch nadert tot (√(a/2) − √(b/2))·x−1/4 zodat het evident is dat de integraal niet kan convergeren voor a ≠ b. Maar dan moet je uiteraard nog steeds aantonen dat de integraal wel convergeert voor a = b.
[ Bericht 0% gewijzigd door Riparius op 10-08-2013 00:41:33 ]
Ik zie niet zo goed hoe dat hypocriet is, en ik snap verder het probleem niet zo.quote:
[..]
Tja, de vraag is wat voor tips je eigenlijk verwacht als een uitgewerkte oplossing er al meteen bij geeft. Je wil niet zelf naar de uitwerking kijken maar kennelijk wel dat iemand je al een stukje van de uitwerking waar je zelf niet naar wil kijken verklapt. Dat is hypocriet.
Dom, maar ik had dat niet ingezien! Het lijkt wel of mijn hersenen niet meer meewerken zodra ik een calculusprobleem ziequote:Interessanter zijn dan tips voor alternatieve oplossingen. Je kunt gemakkelijk laten zien dat de integrand voor x → ∞ asymptotisch nadert tot (√(a/2) − √(b/2))·x−1/4 zodat het evident is dat de integraal niet kan convergeren voor a ≠ b. Maar dan moet je uiteraard nog steeds aantonen dat de integraal wel convergeert voor a = b.
Dank voor de tip!Daar heb ik wel aan gedacht, en dat viel een beetje tegen. Maar ik moet bekennen dat ik dat niet heel lang geprobeerd heb, dus het kan zijn dat ik iets over het hoofd heb gezien.quote:
Heb je al geprobeerd die wortels te rationaliseren? Dit riekt aan alle kanten naar een probleem dat met worteltruuk
√a + √b = (√a + √b)*(√a - √b)/(√a - √b) opgelost dient te worden.
[ Bericht 21% gewijzigd door randomo op 09-08-2013 21:07:52 ]
Ik ben op zoek naar een geschikte functie/formule.
Zie onderstaand plaatje:
Ik ben op zoek naar een formule y = f(x, c)
De blauwe lijn is de curve van de functie.
Deze bestaat nu uit twee lijnstukken en een hoek maar ik wil dat deze vloeiender wordt.
X en y spreken voor zich, beiden gaan van -1 tot 1.
c is gekoppeld aan de rode as en gaat ook van -1 tot 1.
Je kunt zien dat als c=0 de relatie tussen x en y lineair is.
Naarmate c naar -1 of 1 gaat wordt de relatie tussen x en y steeds minder lineair en is er eerst een zeer steile curve die later afvlakt. (of andersom)
Als c -1 of 1 is dan is de blauwe curve extreem gebogen met extreem steile en extreem vlakke helften.
Wanneer dit in twee delen gaat dan is het makkelijk te doen, er zijn dan twee lineaire verbanden waartussen je moet kiezen.
Maar ik ben dus op zoek naar een functie die dit veel vloeiender doet waarbij de blauwe lijn tov de rode as symmetrisch is.
Tevens moet de blauwe lijn binnen het vak -1<x<1 en -1<y<1 blijven.
ik heb wat gespeeld met exponentiële functies maar die waren net niet wat ik zocht.
Heeft iemand tips voor wat ik wel zou kunnen gebruiken?
Zie onderstaand plaatje:
Ik ben op zoek naar een formule y = f(x, c)
De blauwe lijn is de curve van de functie.
Deze bestaat nu uit twee lijnstukken en een hoek maar ik wil dat deze vloeiender wordt.
X en y spreken voor zich, beiden gaan van -1 tot 1.
c is gekoppeld aan de rode as en gaat ook van -1 tot 1.
Je kunt zien dat als c=0 de relatie tussen x en y lineair is.
Naarmate c naar -1 of 1 gaat wordt de relatie tussen x en y steeds minder lineair en is er eerst een zeer steile curve die later afvlakt. (of andersom)
Als c -1 of 1 is dan is de blauwe curve extreem gebogen met extreem steile en extreem vlakke helften.
Wanneer dit in twee delen gaat dan is het makkelijk te doen, er zijn dan twee lineaire verbanden waartussen je moet kiezen.
Maar ik ben dus op zoek naar een functie die dit veel vloeiender doet waarbij de blauwe lijn tov de rode as symmetrisch is.
Tevens moet de blauwe lijn binnen het vak -1<x<1 en -1<y<1 blijven.
ik heb wat gespeeld met exponentiële functies maar die waren net niet wat ik zocht.
Heeft iemand tips voor wat ik wel zou kunnen gebruiken?
2147483647 angels can dance on the point of a needle.
Add one and they will all turn into devils.
Add one and they will all turn into devils.
Ik heb van je rode lijn de x-as gemaakt en de hokjes 1 op 1quote:
Ik ben op zoek naar een geschikte functie/formule.
Heeft iemand tips voor wat ik wel zou kunnen gebruiken?
Dan krijg je telkens bij een gegevens x_i: ax-b voor y=[0..2wortel(2)] en x_i[x_i..2wortel](kan ook [2wortel(2)..x_i] zijn trouwens)tegenover -ax+b voor y=[0...-2wortel(2)] en x_i[x_i..2wortel]
neem nu ax-b dan gaat deze lijn altijd door (2wortel(2),2wortel(2)) en (x_i,0)
Hieruit haal je-> a= 2wortel(2)/(2wortel(2)-x_i) en b=ax_i
x_i laat je lopen van 0 tot 4wortel(2)
dus:
voor een zekere x_i krijgen we:
y_1=2wortel(2)/(2wortel(2)-x_i) x-2wortel(2)/(2wortel(2)-x_i) x_i voor x[x_i...2wortel2] en y[0..2wortel2]
y_2=-2wortel(2)/(2wortel(2)-x_i) x+2wortel(2)/(2wortel(2)-x_i) x_i voor x[x_i...2wortel2] en y[0..-2wortel2]
Kun je het volgen? Het is al ff geleden dat ik met wiskunde bezig ben geweest maar ik denk dat het idee op zich wel iets is waar je iets mee kan.
Ik zou moeten opzoeken hoe je eenvoudig transformaties doet terug naar jou voorbeeld maar er zullen wel anderen zijn waar het allemaal wat verser in het geheugen ligt en waarschijnlijk ook wel met een eenvoudigere rechtstreekse oplossing.
edit:wortel symbool verdwijnt telkens
[ Bericht 3% gewijzigd door Straatklinker op 10-08-2013 04:26:29 ]
Wat jij wil heet interpoleren, en er zijn heel veel verschillende manieren om dit te doen. Welke het meest geschikt is hangt een beetje af van de context, als je echt alleen maar een wat vloeiendere curve wil zou ik vooral een eenvoudige manier gebruiken.quote:
Ik ben op zoek naar een geschikte functie/formule.
Zie onderstaand plaatje:
[ afbeelding ]
Ik ben op zoek naar een formule y = f(x, c)
De blauwe lijn is de curve van de functie.
Deze bestaat nu uit twee lijnstukken en een hoek maar ik wil dat deze vloeiender wordt.
X en y spreken voor zich, beiden gaan van -1 tot 1.
c is gekoppeld aan de rode as en gaat ook van -1 tot 1.
Je kunt zien dat als c=0 de relatie tussen x en y lineair is.
Naarmate c naar -1 of 1 gaat wordt de relatie tussen x en y steeds minder lineair en is er eerst een zeer steile curve die later afvlakt. (of andersom)
Als c -1 of 1 is dan is de blauwe curve extreem gebogen met extreem steile en extreem vlakke helften.
Wanneer dit in twee delen gaat dan is het makkelijk te doen, er zijn dan twee lineaire verbanden waartussen je moet kiezen.
Maar ik ben dus op zoek naar een functie die dit veel vloeiender doet waarbij de blauwe lijn tov de rode as symmetrisch is.
Tevens moet de blauwe lijn binnen het vak -1<x<1 en -1<y<1 blijven.
ik heb wat gespeeld met exponentiële functies maar die waren net niet wat ik zocht.
Heeft iemand tips voor wat ik wel zou kunnen gebruiken?
Een eenvoudige manier die ik ken, bestaat eruit om een aantal n-de graads polynomen te nemen, en daar op bepaalde punten eisen aan te stellen. In dit geval zou ik twee tweedegraads polynomen f1 en f2 nemen, waar je dan de volgende eisen aan kan stellen:
f1(0) = 0 (het punt linksonder)
f1(v) = f2(v) = -v (het punt op de rode lijn)
f2(1) = 1
En verder moet je f1'(v) = f2'(v) hebben om de curve vloeiend (= met continue eerste afgeleide) te houden.
Je kan dan een functie f op het domein [0, 1] met het bereik [0, 1] maken door te definiëren:
f(x) = f1(x) als x in [0, v] en
f(x) = f2(x) als x in (v, 1]
Het is misschien nog onduidelijk hoe je van die eisen aan f1 en f2 naar de polynomen kan komen. Tweedegraads polynomen zijn van de vorm ax2 + bx + c en worden gedefinieerd door de coëffcienten a, b en c. Je hoeft dus alleen de getallen a, b en c te zoeken.
Als je f1(x) = c2x2 + c1x + c0 en f2(x) = d2x2 + d1x + d0 invult en de afgeleide van de polynomen neemt, kan je de voorwaarden mooi uitschrijven tot voorwaarden in de coëfficienten c en d)
(Teken er even een grafiek bij als het niet duidelijk is)
Een hoop interpolatiemanieren zijn gebaseerd op varianten van deze manier: Er wordt vaak een aantal polynomen van een zekere graad genomen, en vervolgens worden er eisen aan de polynomen en hun afgeleiden (dus niet per sé alleen de eerste afgeleide! losjes gezegd zou je kunnen zeggen dat een curve vloeiender wordt als er op de overgangspunten tussen twee polynomen meer afgeleiden gelijk zijn) gesteld, worden de polynomen met hun coëfficienten uitgeschreven, de voorwaarden opgelost zodat we de coëfficienten en dus ook de polynomen weten, en wordt er een functie genomen die steeds op een interval gelijk is aan één van de gevonden polynomen.
Kijk ook eens naar Béziercurves en Hermite curves als je dit interessant vindt. Dit artikel op wikipedia helpt misschien ook als je iets niet begrijpt, al zie ik niet direct dat daar ook eisen aan de afgeleiden worden gesteld. Even googelen kan je ook verder helpen, er is ongetwijfeld veel over polynomen en hun toepassingen in interpolatie geschreven.
Een andere manier is om de grafiek xc (met c een constante die je kan bepalen omdat je wil dat f(v) = v) te herschalen zodat x en y niet van 0 tot 1 maar van -1 tot 1 lopen. Dus dan krijg je zoiets als f(x) = 2 * ((x + 1) / 2)c - 1(hier bijvoorbeeld de grafiek voor c = 2), waar je c bepaalt met de voorwaarde f(v) = -v voor een bepaalde v.
Ik hoop dat je de wiskunde een beetje begrijpt (het is niet heel ingewikkeld als je er even goed naar kijkt, maar sommige dingen zijn misschien wat verwarrend).
[ Bericht 9% gewijzigd door randomo op 10-08-2013 14:20:04 ]
Je zou een kwart van een superellips kunnen gebruiken.quote:
Ik ben op zoek naar een geschikte functie/formule.
Zie onderstaand plaatje:
[ afbeelding ]
Ik ben op zoek naar een formule y = f(x, c)
Wanneer dit in twee delen gaat dan is het makkelijk te doen, er zijn dan twee lineaire verbanden waartussen je moet kiezen.
Maar ik ben dus op zoek naar een functie die dit veel vloeiender doet waarbij de blauwe lijn tov de rode as symmetrisch is.
Tevens moet de blauwe lijn binnen het vak -1<x<1 en -1<y<1 blijven.
ik heb wat gespeeld met exponentiële functies maar die waren net niet wat ik zocht.
Heeft iemand tips voor wat ik wel zou kunnen gebruiken?
Bedankt voor de hulp.
De superellips is precies wat ik zoek.
De superellips is precies wat ik zoek.
2147483647 angels can dance on the point of a needle.
Add one and they will all turn into devils.
Add one and they will all turn into devils.
Is de multipliciteit van beide polen 2 omdat een term in de noemer macht 2 heeft (ik bedoel x^2 in de noemer)? Waarom is de multipliciteit van de wortel van de veeltermbreuk 1? Ik heb een vermoeden dat het komt omdat je geen ^2 kunt vinden voor die wortel (bijvoorbeeld in de teller zie je 2 termen, maar voor geen van beide termen gaat de macht tot 2).
Er zit een fout in je tekst. De polen van de rationale functie in je boek zijn de nulpunten van het polynoom x2(x + 1) in de noemer van het quotiënt. De pool x = 0 heeft multipliciteit 2 maar de pool x = −1 heeft multipliciteit 1.quote:
[ afbeelding ]
Is de multipliciteit van beide polen 2 omdat een term in de noemer macht 2 heeft (ik bedoel x^2 in de noemer)?
Men zegt dat een polynoom P(x) in een variabele x een nulpunt x = x0 met multipliciteit m heeft als P(x) een factor (x − x0)m bevat, maar geen factor (x − x0)m+1. De multipliciteit van een nulpunt x = x0 van een polynoom P(x) is dus precies het aantal factoren (x − x0) dat P(x) bevat.quote:Waarom is de multipliciteit van de wortel van de veeltermbreuk 1? Ik heb een vermoeden dat het komt omdat je geen ^2 kunt vinden voor die wortel (bijvoorbeeld in de teller zie je 2 termen, maar voor geen van beide termen gaat de macht tot 2).
Ik neem aan dat je op de hoogte bent met de stelling dat een polynoom P(x) een nulpunt x = x0 heeft dan en slechts dan als P(x) een factor (x − x0) bevat.
Dankje Riparius, met dat laatste ben ik wel wat bekend.quote:
[..]
Er zit een fout in je tekst. De polen van de rationale functie in je boek zijn de nulpunten van het polynoom x2(x + 1) in de noemer van het quotiënt. De pool x = 0 heeft multipliciteit 2 maar de pool x = −1 heeft multipliciteit 1.
[..]
Men zegt dat een polynoom P(x) in een variabele x een nulpunt x = x0 met multipliciteit m heeft als P(x) een factor (x − x0)m bevat, maar geen factor (x − x0)m+1. De multipliciteit van een nulpunt x = x0 van een polynoom P(x) is dus precies het aantal factoren (x − x0) dat P(x) bevat.
Ik neem aan dat je op de hoogte bent met de stelling dat een polynoom P(x) een nulpunt x = x0 heeft dan en slechts dan als P(x) een factor (x − x0) bevat.
Trouwens, ik had vandaag deze veelterm om in factoren te ontbinden:
http://www.wolframalpha.com/input/?i=x^5-2x^4-2x^3%2B4x^2%2Bx-2
Ik had x=-1 gevonden door gebruik te maken van (som oneven coefficienten van machten van x) = (som even coefficienten van machten van x). Ik had x=2 gevonden door het gewoon te proberen. Daarna wist ik het niet meer en gekeken wat w-alpha zegt. Ik zie nu opeens hoe x=1 gevonden is, dus dat is duidelijk.
Echter, hoe kun je herkennen dat (x+1) en (x-1) beide twee keer als factor voorkomen van de veelterm? Oftewel, hoe weet je dat beide multipliciteit van 2 hebben?
Daarbij, die x=2 was een gok, het had net zo goed wat anders kunnen zijn bij een andere veelterm, hoe zou ik daar dan achter kunnen komen?
Ik weet dat ik met google ver kom, maar jullie weten vast waar ik een berg oefeningen vind voor wiskunde? En daarmee bedoel ik per onderdeel. Dus dat ik een berg logaritmische vragen kan maken, veeltermen, 1e/2e graads functies, beginners differentieren, euclidische deling e.d.
Het zou zeer welkom zijn.
Het zou zeer welkom zijn.
Als je wil kijken of een polynoom waarvan de coëfficiënt van de hoogste macht gelijk is aan 1 gehele getallen als nulpunten heeft, dan hoef je alleen de delers van de constante term te testen, afgezien van het teken. Hier is de coëfficiënt van de hoogste macht x5 inderdaad 1, en de constante term −2, en dan hoef je alleen +1, −1, +2 en −2 te testen.quote:
[..]
Dankje Riparius, met dat laatste ben ik wel wat bekend.
Trouwens, ik had vandaag deze veelterm om in factoren te ontbinden:
http://www.wolframalpha.com/input/?i=x^5-2x^4-2x^3%2B4x^2%2Bx-2
Ik had x=-1 gevonden door gebruik te maken van (som oneven coefficienten van machten van x) = (som even coefficienten van machten van x). Ik had x=2 gevonden door het gewoon te proberen. Daarna wist ik het niet meer en gekeken wat w-alpha zegt. Ik zie nu opeens hoe x=1 gevonden is, dus dat is duidelijk.
Echter, hoe kun je herkennen dat (x+1) en (x-1) beide twee keer als factor voorkomen van de veelterm? Oftewel, hoe weet je dat beide multipliciteit van 2 hebben?
Daarbij, die x=2 was een gok, het had net zo goed wat anders kunnen zijn bij een andere veelterm, hoe zou ik daar dan achter kunnen komen?
Meervoudige wortels opsporen kan lastig zijn, maar hier zou je een polynoomstaartdeling uit kunnen voeren. Door uitproberen weet je dat x = 2 een nulpunt is, en dus moet het polynoom een factor (x − 2) bevatten. Door nu een staartdeling uit te voeren vind je dat het polynoom gelijk is aan
(x − 2)(x4 − 2x2 + 1)
Met behulp van het merkwaardig product (a − b)2 = a2 − 2ab + b2 herken je dan gemakkelijk dat x4 − 2x2 + 1 is te schrijven als
(x2 − 1)2
en met behulp van het merkwaardig product (a + b)(a − b) = a2 − b2 herken je dan weer dat je x2 − 1 kunt schrijven als
(x + 1)(x − 1)
zodat we als ontbinding van het polynoom uiteindelijk krijgen
(x + 1)2(x − 1)2(x − 2)
Het polynoom heeft dus een nulpunt x = −1 met multipliciteit 2, een nulpunt x = 1 met multipliciteit 2, en nog een enkelvoudig nulpunt x = 2.
Over het algemeen geldt dat een polynoom van de graad n precies n nulpunten heeft, als je tenminste ook eventuele complexe nulpunten meetelt én als je meervoudige nulpunten elk net zo vaak meetelt als hun multipliciteit bedraagt.
http://en.m.wikipedia.org/wiki/Newton%E2%80%93Raphson_method
Het bewijs is wat lastig (voor mij), maar toch zeker geen verspilde tijd.
Het bewijs is wat lastig (voor mij), maar toch zeker geen verspilde tijd.
Fervent tegenstander van het korps lasergamers.
Dank je Riparius! Het is weer wat helder. Ik ga nog wat spelen ermee zodat ik in het begin (x-1)(rest van term)=veeltermbreuk heb.
Die Newton regel ga ik vandaag proberen. Dank je.quote:Op maandag 12 augustus 2013 07:57 schreef Amoeba het volgende:
http://en.m.wikipedia.org/wiki/Newton%E2%80%93Raphson_method
Het bewijs is wat lastig (voor mij), maar toch zeker geen verspilde tijd.
SES / 3de machtswortel berekenen met rekenmachine zonder ^ toetsquote:
Dank je Riparius! Het is weer wat helder. Ik ga nog wat spelen ermee zodat ik in het begin (x-1)(rest van term)=veeltermbreuk heb.
[..]
Die Newton regel ga ik vandaag proberen. Dank je.
Het komt hier ter sprake.
Fervent tegenstander van het korps lasergamers.
Notatievraagje. Stel ik heb een funcie Y met parameter x en ik kwadrateer die. Wat is dan de betere notatie (als een van de twee beter is)? Y²(x) of Y(x)²
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Ik heb een vraag.
Ik wil weten of er een correlatie is tussen de openheid van een mondoppervlak en verschillende ecologische factoren.
Als ik bijvoorbeeld deze openheid met de hoogte boven zeeniveau laat berekenen, krijg ik 2 verschillende waarden.
Kennelijk is de correlatie tussen A en B anders dan tussen B en A. Kan dat kloppen?
Ook heb ik de keuze uit Linear Correlation r, Spearman's D, Spearman's rs, Kendall's tau en Partial linear correlation. Ze geven allen een ander getal, maar ik snap niet wat het verschil is. De tekst op wikipedia is alleen maar verwarrend.
Ik wil weten of er een correlatie is tussen de openheid van een mondoppervlak en verschillende ecologische factoren.
Als ik bijvoorbeeld deze openheid met de hoogte boven zeeniveau laat berekenen, krijg ik 2 verschillende waarden.
Kennelijk is de correlatie tussen A en B anders dan tussen B en A. Kan dat kloppen?
Ook heb ik de keuze uit Linear Correlation r, Spearman's D, Spearman's rs, Kendall's tau en Partial linear correlation. Ze geven allen een ander getal, maar ik snap niet wat het verschil is. De tekst op wikipedia is alleen maar verwarrend.
Emotionele exclusiviteit monogamie-adept
Ik weet inmiddels dat ik Partial linear correlation nodig heb, maar ik snap niet waarom ik 2 verschillende waarden krijg.
Iemand een idee?
Iemand een idee?
Emotionele exclusiviteit monogamie-adept
Ik zou zeggen Y(x)². Je zou met Y²(x) ook het volgende kunnen bedoelen:quote:
Notatievraagje. Stel ik heb een funcie Y met parameter x en ik kwadrateer die. Wat is dan de betere notatie (als een van de twee beter is)? Y²(x) of Y(x)²
Maar in principe is er geen officiële notatie, dus je kan doen wat je wil. Als het maar duidelijk is voor de lezer...
Ik zou x hier ook geen parameter noemen, maar een variabele.
Wat is er mis met het woord parameter?
ING en ABN investeerden honderden miljoenen euro in DAPL.
#NoDAPL
#NoDAPL
Het is niet hetzelfde.quote:
Wat is er mis met het woord parameter?
In f(x) = px is p een parameter en x de variabele. Men schrijft ook wel fp(x) om het verschil aan te geven.
De parameter p verandert de vorm van de functie, welke afhankelijk is van een variabele. Ik denk dat ik dat zo wel juist zeg.
Fervent tegenstander van het korps lasergamers.
Het argument van een functie noem je standaard een variabele. Zoals Amoeba aangaf, als in die functie nog een onbekende constante zit, dan noem je dat vaak een 'parameter' (of gewoon 'constante'). (Ik heb nog even gegoogeld, maar ik vind geen echte definities, maar alleen voorbeelden. Het is dus wel discutabel...)quote:
Wat is er mis met het woord parameter?
Het wordt pas wat duidelijker met een simpel praktisch voorbeeld. Stel dat je een verband zoekt tussen tijd en afgelegde weg van een object dat met een constante snelheid beweegt. Je weet dat je een formule van de vorm fa(t)=a*t is. Op het moment dat de snelheid bekend is, weet je wat de waarde van a is, en weet je op iedere t de afgelegde weg y. Hier is a de parameter, en t de variabele.
Maar ik moet toegeven dat het verschil heel subtiel is. Als ik schrijf ft(a)=a*t, dan zou a opeens wel een variabele worden en t een parameter, terwijl het in feite dezelfde functie is. Deze notatie ligt echter meer voor de hand als je je experiment gaat evalueren op een nog onbekend tijdstip t, terwijl je geïnteresseerd bent in de afgelegde weg naargelang je de snelheid varieert.
En om het nog een beetje verwarrender te maken, je hebt ook de zogenaamde "parametervoorstelling", waar bijvoorbeeld de x en y-coördinaat een functie zijn van de tijd. Zoek de parameter in
[ Bericht 1% gewijzigd door thenxero op 14-08-2013 07:19:19 ]
Dus, x en y zijn hier zowel functies als variabelen, en t is zowel variabele als parameter?quote:
[..]
Het argument van een functie noem je standaard een variabele. Zoals Amoeba aangaf, als in die functie nog een onbekende constante zit, dan noem je dat vaak een 'parameter' (of gewoon 'constante'). (Ik heb nog even gegoogeld, maar ik vind geen echte definities, maar alleen voorbeelden. Het is dus wel discutabel...)
Het wordt pas wat duidelijker met een simpel praktisch voorbeeld. Stel dat je een verband zoekt tussen tijd en afgelegde weg van een object dat met een constante snelheid beweegt. Je weet dat je een formule van de vorm fa(t)=a*t is. Op het moment dat de snelheid bekend is, weet je wat de waarde van a is, en weet je op iedere t de afgelegde weg y. Hier is a de parameter, en t de variabele.
Maar ik moet toegeven dat het verschil heel subtiel is. Als ik schrijf ft(a)=a*t, dan zou a opeens wel een variabele worden en t een parameter, terwijl het in feite dezelfde functie is. Deze notatie ligt echter meer voor de hand als je je experiment gaat evalueren op een nog onbekend tijdstip t, terwijl je geïnteresseerd bent in de afgelegde weg naargelang je de snelheid varieert.
En om het nog een beetje verwarrender te maken, je hebt ook de zogenaamde "parametervoorstelling", waar bijvoorbeeld de x en y-coördinaat een functie zijn van de tijd. Zoek de parameter in
Ik dacht altijd dat een variabele een soort overdekkend begrip was (maargoed, zoals je net al aangaf is het discutabel. Volgens mij heb ik ook nog nooit een definitie van variabele of parameter gezien).
| Forum Opties | |
|---|---|
| Forumhop: | |
| Hop naar: | |