[Bèta wiskunde] Huiswerk- en vragentopic

Index

» school, studie en onderwijs

actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
pi_113289428
Post hier weer al je vragen, passies, trauma's en andere dingen die je uit je slaap houden met betrekking tot de wiskunde.

Van MBO tot WO, hier is het topic waar je een antwoord kunt krijgen op je vragen. Vragen over stochastiek in het algemeen en stochastische processen & analyse in het bijzonder worden door sommigen extra op prijs gesteld!

Opmaak:
• met de [tex]-tag kun je Latexcode in je post opnemen om formules er mooier uit te laten zien (uitleg).

Links:
• http://integrals.wolfram.com/index.jsp: site van Wolfram, makers van Mathematica, om online symbolische integratie uit te voeren.
• http://mathworld.wolfram.com/: site van Wolfram met een berg korte wiki-achtige artikelen over wiskundige concepten en onderwerpen, incl. search.
• http://functions.wolfram.com/: site van Wolfram met een berg identiteiten, gerangschikt per soort functie.
• http://scholar.google.com/: Google scholar, zoek naar trefwoorden specifiek in (wetenschappelijke) artikelen. Vaak worden er meerdere versies van hetzelfde artikel gevonden, waarvan één of meer van de website van een journaal en (dus) niet vrij toegankelijk, maar vaak ook een versie die wel vrij van de website van de auteur te halen is.
• http://www.wolframalpha.com Meest geavanceerde rekenmachine van het internet. Handig voor het berekenen van integralen, afgeleides, etc...

OP
pi_113289544
Het lijkt me allereerst handig dat je ons exact vertelt wat de opgave is. Met deze informatie is het zoals Riparius al stelde slechts mogelijk om uit te rekenen wat zijn gemiddelde snelheid was, en op mijn manier of hij niet minimaal 40 km/h diende te sprinten, wat dus niet het geval was omdat hij in 9,79 seconden meer dan 100 meter aflegde.
Dus wat was de extra randvoorwaarde, hoe nam zijn snelheid toe? Was daar een formule voor?

De afgeleide geeft de helling van een functie op een bepaald moment f'(x) = dy/dx Met dy en dx (infinitesimaal?) kleine verschillen. De quotiëntregel is te onthouden met (nat min tan) ofwel Noemer* afgeleide Teller - Teller * afgeleide Noemer (gedeeld door het kwadraat van de noemer). De kettingregel voor een functie f(x)*g(x) -> f'(x)*g(x)+g'(x)*f(x).

Om te weten waar de helling 0 is van een functie, ofwel het maximum/minimum van een grafiek stel je dus de afgeleide functie gelijk aan 0.

Om nu te weten waar de helling maximaal is geef je de tweede afgeleide, ofwel f''(x). Het nulpunt daarvan zal dus het buigpunt geven.

En nu die opgave.

Een klein voorbeeldje van de quotient regel:

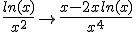
\frac{ln(x)}{x^2} \rightarrow \frac{x-2xln(x)}{x^4}
foto
Je ziet zelf ook wel in dat dit nog een maal te vereenvoudigen is..

[ Bericht 7% gewijzigd door #ANONIEM op 23-06-2012 22:05:03 ]
pi_113290579
quote:
0s.gif
Op zaterdag 23 juni 2012 21:54 schreef thenxero het volgende:

[..]

Ik zou zeggen

∫ sin(x)∙(-cos(x))' dx = -sin(x)∙cos(x) - ∫ -cos(x)∙(sin(x))' dx

[..]

Ik zal nog even toelichten wat ik hier precies doe. Ik gaf slechts de eerste stap.

De regel voor partieel integreren luidt:

∫ u∙dv = u∙v - ∫ v∙du

In dit geval hadden we u = sin(x), dv = sin(x)∙dx, en dus du = cos(x)∙dx, v = -cos(x). Dit geeft:

∫ sin(x)∙d(-cos(x)) = -sin(x)∙cos(x) - ∫ -cos(x)∙d(sin(x))

Nu volgt uit dv = sin(x)∙dx en v = -cos(x) dat d(-cos(x)) = sin(x)∙dx
Evenzo volgt uit du = cos(x)∙dx en u = sin(x) dat d(sin(x)) = cos(x)∙dx

Dus krijgen we:

∫ sin(x)∙sin(x)∙dx = -sin(x)∙cos(x) - ∫ -cos(x)∙cos(x)∙dx

En dus:

∫ sin2(x)∙dx = -sin(x)∙cos(x) + ∫ cos2(x)∙dx
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_113290935
En toch komen we allemaal op hetzelfde uit. Ik begrijp dat ik slechts de haakjes moet zetten, waar ik inderdaad wel vaker commentaar van die 'flutdocent' op heb gekregen.

Maar enfin, als Superky ook nog eens wil reageren binnen het uur..
pi_113291221
Oh zo. Ik heb geleerd om die tussenstap over te slaan, omdat je dan met infinitesimalen werkt zonder bewijs.

Ik onthou die regel ook als ∫ f(x)g'(x) dx = f(x)g(x) - ∫ f'(x)g(x) dx . ;)

[ Bericht 23% gewijzigd door thenxero op 23-06-2012 22:35:14 ]
pi_113291836
quote:
0s.gif
Op zaterdag 23 juni 2012 21:58 schreef Amoeba het volgende:
Het lijkt me allereerst handig dat je ons exact vertelt wat de opgave is. Met deze informatie is het zoals Riparius al stelde slechts mogelijk om uit te rekenen wat zijn gemiddelde snelheid was, en op mijn manier of hij niet minimaal 40 km/h diende te sprinten, wat dus niet het geval was omdat hij in 9,79 seconden meer dan 100 meter aflegde.
Dus wat was de extra randvoorwaarde, hoe nam zijn snelheid toe? Was daar een formule voor?

De afgeleide geeft de helling van een functie op een bepaald moment f'(x) = dy/dx Met dy en dx (infinitesimaal?) kleine verschillen. De quotiëntregel is te onthouden met (nat min tan) ofwel Noemer* afgeleide Teller - Teller * afgeleide Noemer (gedeeld door het kwadraat van de noemer). De kettingregel voor een functie f(x)*g(x) -> f'(x)*g(x)+g'(x)*f(x).

Om te weten waar de helling 0 is van een functie, ofwel het maximum/minimum van een grafiek stel je dus de afgeleide functie gelijk aan 0.

Om nu te weten waar de helling maximaal is geef je de tweede afgeleide, ofwel f''(x). Het nulpunt daarvan zal dus het buigpunt geven.

En nu die opgave.

Een klein voorbeeldje van de quotient regel:

\frac{ln(x)}{x^2} \rightarrow \frac{x-2xln(x)}{x^4}
foto
Je ziet zelf ook wel in dat dit nog een maal te vereenvoudigen is..
Sorry voor de late reactie maar hier komt de opgave:

Omrekenen van eenheden
Het wereldrecord op de 100 m hardlopen is kort geleden gebracht op 9,79 s. Heeft de atleet op enig moment gedurende zijn race met een snelheid groter dan 40 km per uur gelopen?

En verder staat er niks meer.
pi_113292029
Dan kun je keihard zeggen dat je met behulp van de maximaal afgelegde afstand voor een snelheid van 40 km/h deze vraag niet kan beantwoorden. Dat zal dan ook wel het antwoord zijn.

Want:
40 km/h = 40/3,6 = 11,11 m/s * 9,79 > 100m. Ofwel dit is niet te beantwoorden met deze gegevens.
pi_113325123
quote:
0s.gif
Op zaterdag 23 juni 2012 22:27 schreef thenxero het volgende:
Oh zo. Ik heb geleerd om die tussenstap over te slaan, omdat je dan met infinitesimalen werkt zonder bewijs.

Ik onthou die regel ook als ∫ f(x)g'(x) dx = f(x)g(x) - ∫ f'(x)g(x) dx . ;)

Uiteraard sla ik de tussenstap gewoonlijk ook over, maar omdat Amoeba deze tussenstap toch maakte wilde ik even laten zien hoe je dat dan correct op kunt schrijven. Uitgaande van de regel

∫ u∙dv = u∙v - ∫ v∙du

en

u = sin(x), dv = sin(x)∙dx, du = cos(x)∙dx, v = -cos(x)

krijg je direct

∫ sin(x)∙sin(x)∙dx = -sin(x)∙cos(x) - ∫ -cos(x)∙cos(x)∙dx

en dat is ook gebruikelijke manier van werken met de regel voor partieel integreren in deze vorm, zie bijvoorbeeld hier.

Werken met differentialen is niet hetzelfde als werken met infinitesimalen, dus hier is niets inexacts aan, vooropgesteld dat je een formele definitie kunt geven voor (betrekkingen tussen) differentialen die niet steunt op het intuïtieve begrip van 'oneindig kleine' grootheden. Vroeger was dat uiteraard anders, de gehele Leibniz notatie is gebaseerd op de idee van inifinitesimale grootheden.

Toch is de notatie van Leibniz niet stuk te krijgen en heeft deze alle paradigmawisselingen binnen de wiskunde overleefd, en daar zijn goede redenen voor. Deze notatie vereenvoudigt het werken met afgeleiden van samengestelde functies (kettingregel), het werken met de substitutieregel in de integraalrekening (en inderdaad, ook het werken met partieel integreren) en bijvoorbeeld ook het oplossen van bepaalde differentiaalvergelijkingen (scheiding van variabelen).

De substitutieregel (voor onbepaalde integralen) kunnen we weergeven als

∫ f(x)∙dx = ∫ f(g(t))∙g'(t)∙dt

waarbij x = g(t) en dx = g'(t)∙dt zodat d(g(t)) = g'(t)∙dt en we de substitutieregel dus ook kunnen weergeven als

∫ f(x)∙dx = ∫ f(g(t))∙d(g(t))

Als nu F een primitieve is van f dan is dus

∫ f(g(t))∙d(g(t)) = F(g(t)) + C

Hiervan maakte ik gebruik bij enkele herleidingen voor het primitiveren van de secans.

Hebben we f(x) = 1, zodat F(x) = x een primitieve is, dan reduceert dit tot:

∫ d(g(t)) = g(t) + C

zodat je, afgezien van de integratieconstante, kunt zeggen dat ∫ en d inverse operatoren zijn.

Als we hebben y = f(x) waarbij f een differentieerbare functie is van x, dan kunnen we zeggen dat dy/dx = f'(x), en als we het hierbij laten dan zijn dit gewoon twee verschillende notaties voor hetzelfde, namelijk de notatie van Leibniz en de notatie van Lagrange voor de (eerste) afgeleide van de gegeven functie. De uitdrukking dy/dx lijkt verdacht veel op een breuk en om de verwarring nog groter te maken heet dit ook nog een differentiaalquotiënt, terwijl het in de thans gebruikelijke opvatting geen quotiënt is maar een limiet van een differentiequotiënt ∆y/∆x = (f(x + ∆x) - f(x))/∆x voor ∆x → 0.

Maar zo hebben dy en dx afzonderlijk geen betekenis (meer), zodat je nog moet verantwoorden wat je dan precies verstaat onder dy = f'(x)∙dx en hoe dit equivalent is met dy/dx = f'(x) zonder daarbij terug te vallen op intuïtieve begrippen als 'oneindig kleine' grootheden. Er zijn verschillende manieren om het begrip differentiaal te formaliseren maar die zijn niet zo geschikt voor een elementaire behandeling. Je zou echter kunnen afspreken dat je met dy = f'(x)∙dx bedoelt dat de grootheid x (en daarmee ook y) afhangt van een andere variabele, zeg t, zodanig dat dy/dt = f'(x) ∙ dx/dt. Dan is dus y'(t) = f'(x)∙x'(t) oftewel y'(t) = f'(x(t))∙x'(t) en dat is niets anders dan de kettingregel voor y(t) = f(x(t)). Dit is altijd mogelijk, want we kunnen eenvoudig x(t) = t nemen. Betrekkingen tussen differentialen van grootheden kun je zo dus zien als betrekkingen tussen de afgeleiden van die grootheden waarbij de onafhankelijke variabele impliciet is.

We kunnen nu bijvoorbeeld schrijven d(u∙v) = du∙v + u∙dv waarbij u en v functies zijn van een impliciete variabele (i.e. als we deze impliciete variabele t noemen: d(u∙v)/dt = du/dt ∙ v + u ∙ dv/dt) en dit geeft dan ∫ d(u∙v) = ∫ du∙v + ∫ u∙dv en dus ∫ u∙dv = u∙v - ∫ v∙du aangezien ∫ d(u∙v) = u∙v, waarbij we de integratieconstante achterwege laten omdat deze al in ∫ v∙du zit.

[ Bericht 0% gewijzigd door Riparius op 24-06-2012 19:44:32 ]
Maud Wilms - Allemaol
Nadiè Reyhani - The Feet Song
Yasmine - Zus
pi_113325613
Deze post kan dus ook in de bundel. En die tussenstap maak ik omdat ik anders sneller fouten maak.

[ Bericht 47% gewijzigd door #ANONIEM op 24-06-2012 19:26:32 ]
pi_113326560
Deze nog iemand tips?

Hoe laat ik zien dat:

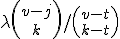
\lambda {v-j \choose k} / {v-t \choose k-t}
foto

gelijk is aan

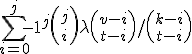
\sum_{i=0}^{j} -1 ^j {j\choose i}\lambda {v-i \choose t-i}/ {k-i \choose t-i}
foto

Achtergrond: beiden zijn uitdrukkingen voor het aantal blokken in een t-(v,k,lambda) design (X, B) dat geen punten overeenkomt met een j-subset van X, J.
De eerste uitdrukking komt van een dubbeltelargument het tweede van het gebruik van het principe van inclusie exclusie. Dit is het enige wat ik me nog afvraag, hoe je ze omschrijft in elkaar.
pi_113326749
Als het beide uitdrukkingen zijn voor hetzelfde aantal, heb je daarmee bewezen dat ze gelijk aan elkaar zijn.
pi_113328189
quote:
0s.gif
Op zondag 24 juni 2012 19:14 schreef Riparius het volgende:

[..]
-knip-
Ik had alleen die notatie nooit gezien, voor de rest ben ik volledig op de hoogte. Dat bewijs dat infinitesimalen bestaan is wel leuk, heb dat een keer gezien. Als het er was geweest had ik ook een vak nonstandaard analyse gedaan ;) .
pi_113328768
quote:
0s.gif
Op zondag 24 juni 2012 19:14 schreef Riparius het volgende:

[..]

Maar zo hebben dy en dx afzonderlijk geen betekenis (meer), zodat je nog moet verantwoorden wat je dan precies verstaat onder dy = f'(x)∙dx en hoe dit equivalent is met dy/dx = f'(x) zonder daarbij terug te vallen op intuïtieve begrippen als 'oneindig kleine' grootheden. Er zijn verschillende manieren om het begrip differentiaal te formaliseren maar die zijn niet zo geschikt voor een elementaire behandeling. Je zou echter kunnen afspreken dat je met dy = f'(x)∙dx bedoelt dat de grootheid x (en daarmee ook y) afhangt van een andere variabele, zeg t, zodanig dat dy/dt = f'(x) ∙ dx/dt. Dan is dus y'(t) = f'(x)∙x'(t) oftewel y'(t) = f'(x(t))∙x'(t) en dat is niets anders dan de kettingregel voor y(t) = f(x(t)). Dit is altijd mogelijk, want we kunnen eenvoudig x(t) = t nemen. Betrekkingen tussen differentialen van grootheden kun je zo dus zien als betrekkingen tussen de afgeleiden van die grootheden waarbij de onafhankelijke variabele impliciet is.
Als je de afgeleide van Fréchet gebruikt, hebben dy en dx wel gewoon een betekenis, net als dy/dx.
pi_113330258
quote:
0s.gif
Op zondag 24 juni 2012 19:47 schreef Oneironaut het volgende:
Deze nog iemand tips?

Hoe laat ik zien dat:

\lambda {v-j \choose k} / {v-t \choose k-t}
foto

gelijk is aan

\sum_{i=0}^{j} -1 ^j {j\choose i}\lambda {v-i \choose t-i}/ {k-i \choose t-i}
foto

Achtergrond: beiden zijn uitdrukkingen voor het aantal blokken in een t-(v,k,lambda) design (X, B) dat geen punten overeenkomt met een j-subset van X, J.
De eerste uitdrukking komt van een dubbeltelargument het tweede van het gebruik van het principe van inclusie exclusie. Dit is het enige wat ik me nog afvraag, hoe je ze omschrijft in elkaar.
Het lijkt me toch dat je hier het een en ander wel kunt vereenvoudigen. Schrijf die binomiaalcoëfficiënten maar eens uit in faculteiten. In beide uitdrukkingen zie je dan al een (k-t)!/(v-t)! verschijnen, en in die onderste uitdrukking valt er in elke term een (t-i)! tegen elkaar weg.
pi_113341640
quote:
0s.gif
Op zondag 24 juni 2012 19:47 schreef Oneironaut het volgende:
Deze nog iemand tips?

Hoe laat ik zien dat:

\lambda {v-j \choose k} / {v-t \choose k-t}
foto

gelijk is aan

\sum_{i=0}^{j} -1 ^j {j\choose i}\lambda {v-i \choose t-i}/ {k-i \choose t-i}
foto

Achtergrond: beiden zijn uitdrukkingen voor het aantal blokken in een t-(v,k,lambda) design (X, B) dat geen punten overeenkomt met een j-subset van X, J.
De eerste uitdrukking komt van een dubbeltelargument het tweede van het gebruik van het principe van inclusie exclusie. Dit is het enige wat ik me nog afvraag, hoe je ze omschrijft in elkaar.
quote:
0s.gif
Op zondag 24 juni 2012 20:52 schreef thabit het volgende:

[..]

Het lijkt me toch dat je hier het een en ander wel kunt vereenvoudigen. Schrijf die binomiaalcoëfficiënten maar eens uit in faculteiten. In beide uitdrukkingen zie je dan al een (k-t)!/(v-t)! verschijnen, en in die onderste uitdrukking valt er in elke term een (t-i)! tegen elkaar weg.
Het moest overigens zijn (macht i niet j):

\sum_{i=0}^{j} -1 ^i {j\choose i}\lambda {v-i \choose t-i}/ {k-i \choose t-i}
foto
Dit is

\frac{(k-t)!}{(v-t)!}\lambda\sum_{i=0}^{j}-1^i\frac{j!}{i!(j-i)!} \frac{(v-i)!}{(k-i)!}
foto

Dus blijft over:
\frac{(v-j)!}{(v-j-k)!k!}=?=\sum_{i=0}^j-1^i\frac{j!(v-i)!}{i!(j-i)!(k-i)!}
foto
Oh en
j\leq t
foto

Maar die som.... welke regel kan ik daar voor gebruiken?
Iets van: http://mathworld.wolfram.com/BinomialSums.html ?

[ Bericht 0% gewijzigd door Oneironaut op 24-06-2012 23:32:01 ]
pi_113343389
Ik zou
j\choose j-i
foto laten staan, en
(v-i)!/(k-i)!
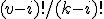foto kun je schrijven als
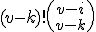(v-k)!{v-i\choose v-k
foto. De factor (v-k)! heb je ook in die eerste formule. Op die manier krijg je al een heel wat eenvoudigere identiteit die je moet bewijzen.
pi_113359019
Als het goed is krijg je dus iets met de sommatie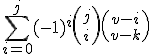
\sum_{i=0}^j(-1)^i{j \choose i}{v-i\choose v-k}
foto erin. Ga even na of dit klopt. Dit soort sommen zijn namelijk vrij algemeen uit te werken, als je het truukje weet.
pi_113364256
Nog maar een vraagje, want ik loop hier vast.

om deze externe inhoud weer te geven is het noodzakelijk dat je toestemming geeft voor het gebruik van tracking en social mediacookies.
Ja toon me deze inhoud
ik accepteer de cookies.
meer informatie


Hoe kom je op die 17,55% (onderste zin)? Want dat staat er niet bij.
pi_113365003
Misschien met je GR, of met een normale benadering?
pi_113365307
quote:
0s.gif
Op maandag 25 juni 2012 14:53 schreef thenxero het volgende:
Misschien met je GR, of met een normale benadering?
GR niet, dat laatste dan denk ik.
pi_113367030
Met de normale benadering krijg ik 17.2%. Lijkt mij prima maar ik weet niet wat ze van je verwachten. Omdat exact te doen lijkt me vrij vervelend.
pi_113367426
quote:
0s.gif
Op maandag 25 juni 2012 15:32 schreef thenxero het volgende:
Met de normale benadering krijg ik 17.2%. Lijkt mij prima maar ik weet niet wat ze van je verwachten. Omdat exact te doen lijkt me vrij vervelend.
Kan zijn dat ze dan het gemiddelde hebben genomen van de normale benadering voor X = 11 en X = 10. Exact hoeft volgens mij niet.
  maandag 25 juni 2012 @ 15:52:32 #23
75592 GlowMouse
l'état, c'est moi
pi_113368004
Het is echt een exact resultaat, lijkt me dus GR-werk of pc-werk.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pi_113368264
quote:
11s.gif
Op maandag 25 juni 2012 15:52 schreef GlowMouse het volgende:
Het is echt een exact resultaat, lijkt me dus GR-werk of pc-werk.
Oh dan heeft de docent het met de GR gedaan denk ik. Maar dat mogen wij niet.
pi_113368524
Simpel vraagje denk ik:

Wat heeft de waarde constant voor een betekenis in een logistic regression?

om deze externe inhoud weer te geven is het noodzakelijk dat je toestemming geeft voor het gebruik van tracking en social mediacookies.
Ja toon me deze inhoud
ik accepteer de cookies.
meer informatie


[ Bericht 17% gewijzigd door Soldier2000 op 25-06-2012 17:19:13 ]
BlaBlaBla
actieve topics nieuwe topics
abonnement Unibet Coolblue Bitvavo
[Bèta wiskunde] Huiswerk- en vragentopic
Index

» school, studie en onderwijs

Forum Opties
Forumhop:
Hop naar:
(afkorting, bv 'KLB')

Het lijkt erop dat je onze advertenties blokkeert

Dat begrijpen we, maar is wel erg jammer. Je kunt FOK! namelijk wel gratis LEZEN, maar we kunnen FOK! niet gratis MAKEN. De inkomsten van de advertenties zorgen ervoor dat we de kosten van de site kunnen dragen zodat je ook morgen FOK! nog kunt bezoeken.

Zou je willen overwegen om voor FOK! een uitzondering te maken in je adblocker (of andere middelen die onze ads blokkeren)? Je krijgt deze melding dan nooit meer te zien.

Ja, ik wil fok.nl whitelisten, laat me zien hoe

Ik neem liever een premium account zodat ik geen advertenties hoef te zien (je moet eerst inloggen)
Ja, breng me naar de shop