[Bèta wiskunde] Huiswerk- en vragentopic

maandag 21 mei 2012 @ 19:38:21 #251

Amoeba

Floydiaan.

quote:
Op maandag 21 mei 2012 18:43 schreef thenxero het volgende:

[..]

De leukste opgaves vind ik toch eigenlijk opgaves waarbij je weinig algebra nodig hebt, maar het probleem gewoon heel handig moet aanpakken waardoor een schijnbaar onmogelijk probleem opeens heel eenvoudig wordt.

De beste opgaves zijn hordes vol algebra van een schijnbaar eenvoudige opgave. Zoals die bol, ik dacht serieus: Dat wordt peanuts.

Zelfs beide Wiskunde docenten op het VWO hier kennen die formule niet... (Calando)

Fervent tegenstander van het korps lasergamers.

maandag 21 mei 2012 @ 19:42:25 #252

thenxero

quote:
Op maandag 21 mei 2012 19:26 schreef Amoeba het volgende:

[..]

Waarom maar dan ook waarom zou je a eruit halen?

Zodat je hem kan invullen... bijvoorbeeld als volgt:
(noteer even x=2/sqrt(29))
$O(\arccos(x))=2\sin(\arccos(x))\cos(\arccos(x))+\sin(\arccos(x))\sqrt{21+4\cos^2(\arccos(x))}$
$=2x\sqrt{1-x^2}+\sqrt{1-x^2}\sqrt{21+4x^2}$
$=\sqrt{1-x^2}(2x+\sqrt{21+4x^2})$
$=\frac{5}{\sqrt{29}}(\frac{4}{\sqrt{29}}+\sqrt{21+\frac{4}{29}})$
$=\frac{20}{29}+\frac{5}{\sqrt{29}}\sqrt{\frac{625}{29}}$
$=\frac{145}{29}=5$

Poepoe, wat een typwerk

Ik maak dus gebruik van sin(arccos(x))=sqrt(1-x^2). Dat kan je bewijzen met sin² z + cos² z =1 en dan z=arcos(x) te nemen.

[ Bericht 3% gewijzigd door thenxero op 21-05-2012 19:47:48 ]

maandag 21 mei 2012 @ 19:43:29 #253

thenxero

quote:
Op maandag 21 mei 2012 19:38 schreef Amoeba het volgende:

[..]

Zelfs beide Wiskunde docenten op het VWO hier kennen die formule niet... (Calando)

Cardano. En ze hebben er hopelijk wel van gehoord, maar kennen het niet uit hun hoofd. De meeste wiskundeprofessors zullen die formule ook niet uit hun hoofd kennen

.

maandag 21 mei 2012 @ 19:51:21 #254

Amoeba

Floydiaan.

Oh, heet die gast Cardano.

Ik kan me toch herinneren dat wij hem anders uitgerekend hadden.
Nadat je inderdaad die discriminant had genomen en de oplossingen had, na wat geschuifel kwamen we toch op 2 nuttige vergelijkingen uit. Ik kom er morgen op terug. Na afgelopen nacht m'n kop over die bol gebroken te hebben mag ik wel wat uurtjes inhalen.

Maar het zal ongetwijfeld kloppen! 2/r29 komt inderdaad heel bekend voor

Trouwens, de app van Wolframalpha voor Android is ook wel echt geil.

Fervent tegenstander van het korps lasergamers.

maandag 21 mei 2012 @ 19:56:19 #255

thenxero

quote:
Op maandag 21 mei 2012 19:51 schreef Amoeba het volgende:
Oh, heet die gast Cardano.

Ik kan me toch herinneren dat wij hem anders uitgerekend hadden.
Nadat je inderdaad die discriminant had genomen en de oplossingen had, na wat geschuifel kwamen we toch op 2 nuttige vergelijkingen uit. Ik kom er morgen op terug. Na afgelopen nacht m'n kop over die bol gebroken te hebben mag ik wel wat uurtjes inhalen.

Maar het zal ongetwijfeld kloppen! 2/r29 komt inderdaad heel bekend voor

Ja die gast heet Cardano. Ook wel grappig dat vanwege die formule de imaginaire getallen "in" zijn geraakt. Want toen realiseerde men zich dat imaginaire getallen wel degelijk betekenis/nut hadden, omdat het kan gebeuren dat je met die formule negatieve getallen in de wortel kan krijgen, terwijl de oplossing toch reëel is.

Er zijn inderdaad meerdere manieren (zoals wel vaker met gonio). Je zou bijvoorbeeld alles als sin kunnen schrijven, en dan krijg je een kwadratische vergelijking in termen van sinus.

maandag 21 mei 2012 @ 20:57:15 #256

Don_Vanelli

...

quote:
Op maandag 21 mei 2012 19:42 schreef thenxero het volgende:

[..]

Zodat je hem kan invullen... bijvoorbeeld als volgt:
(noteer even x=2/sqrt(29))
$O(\arccos(x))=2\sin(\arccos(x))\cos(\arccos(x))+\sin(\arccos(x))\sqrt{21+4\cos^2(\arccos(x))}$
$=2x\sqrt{1-x^2}+\sqrt{1-x^2}\sqrt{21+4x^2}$
$=\sqrt{1-x^2}(2x+\sqrt{21+4x^2})$
$=\frac{5}{\sqrt{29}}(\frac{4}{\sqrt{29}}+\sqrt{21+\frac{4}{29}})$
$=\frac{20}{29}+\frac{5}{\sqrt{29}}\sqrt{\frac{625}{29}}$
$=\frac{145}{29}=5$

Poepoe, wat een typwerk

Ik maak dus gebruik van sin(arccos(x))=sqrt(1-x^2). Dat kan je bewijzen met sin² z + cos² z =1 en dan z=arcos(x) te nemen.

Meh, ik zat in de trein, maar ik heb hier op papier dezelfde berekening staan

maandag 21 mei 2012 @ 21:04:50 #257

Don_Vanelli

...

foutje, berekening is onderweg..

maandag 21 mei 2012 @ 21:17:16 #258

Wicky15

It Wasn't Me

stukje inleiding: Van een parabolöide is de straal a en de hoogte 3a. De inhoud is te berekenen met de formule inhoud = 4,71a³ (tot de macht 3 voor degene die het niet kunnen lezen)

vraag: Bereken de inhoud in cm³ van een parabolöide met een hoogte van 12 cm en een straal van 4 cm. Rond af op twee decimalen.

Hier snap ik werkelijk geen kut van, dus als iemand mij wil helpen, graag!

maandag 21 mei 2012 @ 21:19:04 #259

thenxero

quote:
Op maandag 21 mei 2012 21:17 schreef Wicky15 het volgende:
stukje inleiding: Van een parabolöide is de straal a en de hoogte 3a. De inhoud is te berekenen met de formule inhoud = 4,71a³ (tot de macht 3 voor degene die het niet kunnen lezen)

vraag: Bereken de inhoud in cm³ van een parabolöide met een hoogte van 12 cm en een straal van 4 cm. Rond af op twee decimalen.

Hier snap ik werkelijk geen kut van, dus als iemand mij wil helpen, graag!

a=4, en invullen

maandag 21 mei 2012 @ 21:24:28 #260

Wicky15

It Wasn't Me

quote:
Op maandag 21 mei 2012 21:19 schreef thenxero het volgende:

[..]

a=4, en invullen

Die klopt, thanks. Zou je misschien willen uitleggen waarom a=4 ?

maandag 21 mei 2012 @ 21:24:36 #261

Don_Vanelli

...

Voor de volledigheid:

$f(x) = \sin(2x) + \sin(x)\sqrt{21+4\cos^2(x)}$
$= 2\sin(x)\cos(x) + \sin(x)\sqrt{21+4\cos^2(x)}$
$= \sin(x)\left(2\cos(x) + \sqrt{21+4\cos^2(x)}\right)$

Differentieren geeft

$\frac{df}{dx} = \sin(x)\left(-2\sin(x) + \frac{-4\sin(x)\cos(x)}{\sqrt{21+4\cos^2(x)}}\right) + \cos(x)\left(2\cos(x)+\sqrt{21+4\cos^2(x)}\right)$
$= 2\cos(x)^2 - 2\sin(x)^2 + \frac{\cos(x)(4\cos^2(x)-4\sin^2(x)+21)}{\sqrt{21+4\cos^2(x)}}$
$4\cos^2(x) - 2 + \frac{\cos(x)(8\cos^2(x)+17)}{\sqrt{21+4\cos^2(x)}} = 0$ (1)

$t = \cos^2(x)$ geeft:

$(2 - 4t)^2 = \frac{t(8t+17)^2}{21+4t}$
$(21+4t)(2 - 4t)^2 = t(8t+17)^2$
$64t^3 + 272t^2 - 320t + 84 = 64t^3 + 272t^2+289t$
$84t=609$
$t = \frac{4}{29}$

dus

$\cos^2(x) = \frac{4}{29}$
$x = \arccos\left(\pm\sqrt{\frac{4}{29}}\right)$
$x = \arccos\left(-\sqrt{\frac{4}{29}}\right)$ voldoet niet aan (1), dus

$x = \arccos\left(\sqrt{\frac{4}{29}}\right)$

maandag 21 mei 2012 @ 21:26:24 #262

thenxero

quote:
Op maandag 21 mei 2012 21:24 schreef Don_Vanelli het volgende:
...

Precies wat ik ook had

maandag 21 mei 2012 @ 21:26:35 #263

Wicky15

It Wasn't Me

Van een parabolöide is de hoogte drie keer de straal. De inhoud is 185 cm³.
Bereken de straal van de parabolöide in mm.

Deze weet ik ook niet..

maandag 21 mei 2012 @ 21:27:26 #264

Don_Vanelli

...

quote:
Op maandag 21 mei 2012 21:26 schreef Wicky15 het volgende:
Van een parabolöide is de hoogte drie keer de straal. De inhoud is 185 cm³.
Bereken de straal van de parabolöide in mm.

Deze weet ik ook niet..

een paraboloïde is een parabool die om de y-as is gewenteld?

maandag 21 mei 2012 @ 21:28:03 #265

thenxero

quote:
Op maandag 21 mei 2012 21:26 schreef Wicky15 het volgende:
Van een parabolöide is de hoogte drie keer de straal. De inhoud is 185 cm³.
Bereken de straal van de parabolöide in mm.

Deze weet ik ook niet..

4,71a³ = 185 en dan oplossen voor a, en a is de straal (in cm).

maandag 21 mei 2012 @ 21:30:14 #266

Wicky15

It Wasn't Me

quote:
Op maandag 21 mei 2012 21:27 schreef Don_Vanelli het volgende:

[..]

een paraboloïde is een parabool die om de y-as is gewenteld?

Yup.

maandag 21 mei 2012 @ 21:30:16 #267

thenxero

quote:
Op maandag 21 mei 2012 21:27 schreef Don_Vanelli het volgende:

[..]

een paraboloïde is een parabool die om de y-as is gewenteld?

Ja. En ik denk dat ie bedoelt dat ie afgezaagd wordt op een hoogte 3a en dat de straal daar dan a is.

maandag 21 mei 2012 @ 21:33:57 #268

Don_Vanelli

...

quote:
Op maandag 21 mei 2012 21:30 schreef thenxero het volgende:

[..]

Ja. En ik denk dat ie bedoelt dat ie afgezaagd wordt op een hoogte 3a en dat de straal daar dan a is.

Ergens vrees ik dan dat $\pi=3,14$ wordt genomen

maandag 21 mei 2012 @ 21:34:21 #269

Wicky15

It Wasn't Me

quote:
Op maandag 21 mei 2012 21:28 schreef thenxero het volgende:

[..]

4,71a³ = 185 en dan oplossen voor a, en a is de straal (in cm).

Die klopt ook. Hartstikke bedankt

maandag 21 mei 2012 @ 21:40:41 #270

Don_Vanelli

...

quote:
Op maandag 21 mei 2012 21:34 schreef Wicky15 het volgende:

[..]

Die klopt ook. Hartstikke bedankt

Behalve dan dat de inhoud van een dergelijk object wordt gegeven door

$\frac{3}{2}\pi a^3$

maandag 21 mei 2012 @ 21:46:04 #271

Wicky15

It Wasn't Me

quote:
Op maandag 21 mei 2012 21:40 schreef Don_Vanelli het volgende:

[..]

Behalve dan dat de inhoud van een dergelijk object wordt gegeven door

$\frac{3}{2}\pi a^3$

Ik zit in havo3, dit gaat me iets te ver

maandag 21 mei 2012 @ 21:48:51 #272

VanishedEntity

Kan er iemand mij even helpen met het root denesting algoritme?

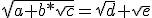
$\sqrt{a + b*\sqrt{c}} = \sqrt{d} + \sqrt{e}$

Kwadrateren levert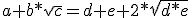 $a + b*\sqrt{c} = d + e + 2*\sqrt{d*e}$

Nu het rationale deel in irrationale deel afzonderlijk links en rechts van de vgl. aan elkaar gelijk stellen:

a = d + e

en vervolgens loop ik hier vast:

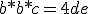
$b*b*c = 4de$

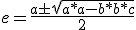
Wiki zegt vervolgens: $e = \frac{a \pm \sqrt{a*a - b*b*c}}{2}$

Ik zie de gemaakte stappen to-taal niet, sorry....

[ Bericht 8% gewijzigd door VanishedEntity op 21-05-2012 22:02:00 ]

maandag 21 mei 2012 @ 21:51:30 #273

Don_Vanelli

...

quote:
Op maandag 21 mei 2012 21:46 schreef Wicky15 het volgende:

[..]

Ik zit in havo3, dit gaat me iets te ver

Kies wiskunde B, doe daarna het vwo, dan zie je het vanzelf

maandag 21 mei 2012 @ 21:53:17 #274

Don_Vanelli

...

quote:
Op maandag 21 mei 2012 21:48 schreef VanishedEntity het volgende:
Kan er iemand mij even helpen met het root denesting algoritme?

$\sqrt{a + b*\sqrt{c}} = \sqrt{d} + \sqrt{e}$

Kwadrateren levert $a + b*\sqrt{c} = d + e + 2*\sqrt{d*e}$

Nu het rationale deel in irrationale deel afzonderlijk links en rechts van de vgl. aan elkaar gelijk stellen:

a = d + e

en vervolgens loop ik hier vast:

$b*b*c = 4de$

http://en.wikipedia.org/w(...)ting_nested_radicals

maandag 21 mei 2012 @ 21:58:37 #275

kutkloon7

quote:
Op maandag 21 mei 2012 18:43 schreef thenxero het volgende:

[..]

De leukste opgaves vind ik toch eigenlijk opgaves waarbij je weinig algebra nodig hebt, maar het probleem gewoon heel handig moet aanpakken waardoor een schijnbaar onmogelijk probleem opeens heel eenvoudig wordt.

Uhu

Een tijdje geleden zat ik ook wat te rekenen met formules van de vorm:
$\sum_{k=0}{n}{k^m}$

En tot mijn stomme verbazing lukte het om een recurrente formule te geven voor de coëfficienten van een polynoom in n met graad m + 1, zodat deze polynoom voor elke waarde (>= 0) dezelfde waarde heeft als de som.

Nu kan dit ook door gewoon de waardes die de som aanneemt te observeren en een polynoom van graad m + 1 te zoeken die de dezelfde waardes aanneemt, maar ik vond het toch een mooi resultaat

Forum Opties
Forumhop:
Hop naar:	(afkorting, bv 'KLB')

» school, studie en onderwijs

» school, studie en onderwijs