[Bčta wiskunde] Huiswerk- en vragentopic

Index

» school, studie en onderwijs

actieve topics nieuwe topics
abonnement Unibet Coolblue
pi_110058430
quote:
0s.gif Op zondag 8 april 2012 15:04 schreef ulq het volgende:

[..]
Ooh sorry man, had ik allemaal niet gelezen, veel te lang stuk en niet bruikbaar voor mijn vraag.
Dat stuk beantwoord precies jouw vraag. Als je iets echt wil snappen dan moet je er altijd moeite voor doen. Niks is gratis.
pi_110058495
quote:
0s.gif Op zondag 8 april 2012 15:16 schreef thenxero het volgende:

[..]

Dat stuk beantwoord precies jouw vraag. Als je iets echt wil snappen dan moet je er altijd moeite voor doen. Niks is gratis.
Nee, daar gaat het niet om. In dat topic ging het over logaritmen, wat dat precies waren. Gewoon een heel laag niveau vraag. Vervolgens zei Riparius dat het onderwijs zo slecht was e.d. en was hij met zo'n andere wiskundige aan het praten. Dat stuk wat hij daar plaatste had eigenlijk niks te maken met het topic, vandaar heb ik het ook niet helemaal doorgelezen.
pi_110058552
quote:
0s.gif Op zondag 8 april 2012 15:18 schreef ulq het volgende:

[..]

Nee, daar gaat het niet om. In dat topic ging het over logaritmen, wat dat precies waren. Gewoon een heel laag niveau vraag. Vervolgens zei Riparius dat het onderwijs zo slecht was e.d. en was hij met zo'n andere wiskundige aan het praten. Dat stuk wat hij daar plaatste had eigenlijk niks te maken met het topic, vandaar heb ik het ook niet helemaal doorgelezen.
Bram had in dat topic dezelfde vraag als jij nu hier stelt. Riparius legt uit waarom
\int_a^b f(x) = F(b)-F(a)
waarbij F de primitieve van f is (dit geldt alleen onder de bepaalde voorwaarden). Die identiteit is natuurlijk erg handig als je integralen wil berekenen.
pi_110058676
Ok maar het klopt dus wel dat :

\int_a^b f(x) = F(b)-F(a) = Oppervlakte van interval [a,b] tussen de x-as en f(x)

toch? ^^
pi_110058825
quote:
0s.gif Op zondag 8 april 2012 15:24 schreef ulq het volgende:
Ok maar het klopt dus wel dat :

\int_a^b f(x) = F(b)-F(a) = Oppervlakte van interval [a,b] tussen de x-as en f(x)

toch? ^^
Bijna, maar niet helemaal. Want in een integraal wordt oppervlakte boven de x-as positief gerekend, maar oppervlakte onder de x-as negatief.

Als f dus een niet-negatieve functie is op [a,b] dan heb je gelijk.
pi_110058899
quote:
0s.gif Op zondag 8 april 2012 15:27 schreef thenxero het volgende:

[..]

Bijna, maar niet helemaal. Want in een integraal wordt oppervlakte boven de x-as positief gerekend, maar oppervlakte onder de x-as negatief.

Als f dus een niet-negatieve functie is op [a,b] dan heb je gelijk.
Ok dankje dan snap ik het allemaal opzich wel. Alleen snap ik het nut van een primitieve functie nog niet helemaal, maar dat is ook geen vereiste voor mijn niveau.

Thnx!
pi_110058968
quote:
0s.gif Op zondag 8 april 2012 15:29 schreef ulq het volgende:

[..]

Ok dankje dan snap ik het allemaal opzich wel. Alleen snap ik het nut van een primitieve functie nog niet helemaal, maar dat is ook geen vereiste voor mijn niveau.

Thnx!
Het nut is juist wel duidelijk: je kan op die manier integralen berekenen. Als je de reden wil weten waarom het zo werkt, dan moet je Riparius' post erop nalezen.
pi_110059140
klopt, de toepassing weet ik nu, ik snap alleen nog niet waarom dat zo werkt, oftewel waarom : 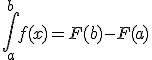\int_a^b f(x) = F(b)-F(a)

maar ik zal dat stukkie idd nog wel ff lezen.
pi_110062763
Hallon, ik heb weer eens een vraag en aangezien ik hier altijd prima geholpen wordt, stel ik mijn vraag hier nog maar een keer. Ik ben het boek A=B aan het lezen. Op bladzijde 55 (65 in het bestand) zit een stukje wat ik niet helemaal begrijp. Men probeert hier de som
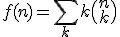
f(n) = \sum_{k}{k\binom{n}{k}}
te evalueren. Ik zal voor de eenvoudigheid doen wat ze daar ook dan, maar dan met de som
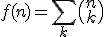
f(n) = \sum_{k}{\binom{n}{k}}
Eerst wordt de functie waarover gesommeerd wordt bekeken, daar wordt dit de sommand/summand genoemd:
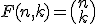
F(n, k) = \binom{n}{k}
Dan wordt er gezocht naar een recurrente betrekking waaraan de sommand voldoet, bijvoorbeeld:
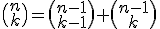
\binom{n}{k}=\binom{n - 1}{k -1}+\binom{n - 1}{k}
dus ook:
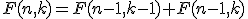
F(n, k) = F(n - 1, k - 1) + F(n - 1, k)
Dan wordt hiervan de sommatie over alle integers k genomen:
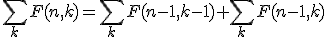
\sum_{k}{F(n, k)} = \sum_{k}{F(n - 1, k - 1)} + \sum_{k}{F(n - 1, k)}
en omdat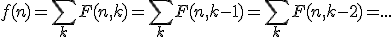 f(n)=\sum_{k}{F(n, k)} = \sum_{k}{F(n, k - 1) = \sum_{k}{F(n, k - 2)} = ...
kunnen we dit vereenvoudigen naar:
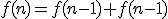
f(n) = f(n - 1) + f(n - 1)
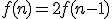
f(n) = 2f(n - 1)
dus als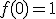 f(0) = 1
is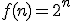 f(n) = 2^n de oplossing van deze vergelijking. Ik geloof dat ik dit op zich begrijp, maar als ik het goed begrijp is dit nog steeds een oneindige som (een sommatie over alle integers k). Ik begrijp het nut hier niet zo van, volgens mij heb je liever een formule voor een eindige sommatie. Het viel me ook op dat je met het binomium van Newton natuurlijk gelijk kan inzien dat
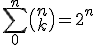
\sum_0^n{\binom{n}{k}}=2^n
Wat natuurlijk een veel nuttigere formule is, en waar ook nog eens hetzelfde uitkomt, maar over een sommatie met eindige grenzen. Om tot deze oplossing te komen kan je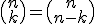 \binom{n}{k} = \binom{n}{n - k} gebruiken, maar in het algemeen lijkt het me dat je niet zoiets kan toepassen. Bovendien kan je dan te maken hebben met negatieve faculteiten, waarvan ik niet weet of dat een probleem is (?).

Begrijp ik het goed en is deze methode alleen bruikbaar om oneindige sommen te evalueren?

[ Bericht 0% gewijzigd door kutkloon7 op 08-04-2012 23:21:43 ]
pi_110063018
De som is eindig, want (n boven k) is 0 voor k > n.
  zondag 8 april 2012 @ 17:32:19 #161
75592 GlowMouse
l'état, c'est moi
pi_110063054
ik mis de integrator (dx) in alle integralen hierboven :'(

De faculteit is alleen voor niet-negatieve gehele getallen gedefinieerd, maar je zou de gamma-functie kunnen gebruiken om de definitie uit te breiden naar negatieve getallen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pi_110063552
quote:
0s.gif Op zondag 8 april 2012 17:32 schreef GlowMouse het volgende:
De faculteit is alleen voor niet-negatieve gehele getallen gedefinieerd, maar je zou de gamma-functie kunnen gebruiken om de definitie uit te breiden naar negatieve getallen.
Dat zal niet gaan werken. De Gamma-functie is immers singulier voor negatieve gehele getallen.
pi_110063647
quote:
0s.gif Op zondag 8 april 2012 17:32 schreef GlowMouse het volgende:
ik mis de integrator (dx) in alle integralen hierboven :'(
De hele tijd dx schrijven is voor beginners ;)
  zondag 8 april 2012 @ 17:56:38 #164
75592 GlowMouse
l'état, c'est moi
pi_110063737
quote:
0s.gif Op zondag 8 april 2012 17:54 schreef thenxero het volgende:

[..]

De hele tijd dx schrijven is voor beginners ;)
wacht maar tot je iets anders tegenkomt als een Riemann-integraal
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pi_110064964
quote:
7s.gif Op zondag 8 april 2012 17:56 schreef GlowMouse het volgende:

[..]

wacht maar tot je iets anders tegenkomt als een Riemann-integraal
Bij lebesgue integralen zet ik ook niet de hele tijd de maat en variabele neer :) . Dan is het uit de context meestal ook wel duidelijk welke maat je gebruikt en wat je variabele is.
pi_110079724
quote:
0s.gif Op zondag 8 april 2012 17:31 schreef thabit het volgende:
De som is eindig, want (n boven k) is 0 voor k > n.
quote:
0s.gif Op zondag 8 april 2012 17:32 schreef GlowMouse het volgende:
De faculteit is alleen voor niet-negatieve gehele getallen gedefinieerd, maar je zou de gamma-functie kunnen gebruiken om de definitie uit te breiden naar negatieve getallen.
Ik begrijp nu nog steeds niet zo goed wat precies het 'bereik' van de integraalsommatie is. Zou je kunnen zeggen dat f(n) de som is van alle f(n, k) waar k alle aanneemt zodat f(n, k) gedefinieerd is?
Dit lijkt me wel een logisch, volgens mij zijn de resultaten dan nog steeds geldig :).

[ Bericht 1% gewijzigd door kutkloon7 op 09-04-2012 17:13:11 ]
  zondag 8 april 2012 @ 23:37:30 #167
75592 GlowMouse
l'état, c'est moi
pi_110080824
quote:
2s.gif Op zondag 8 april 2012 23:19 schreef kutkloon7 het volgende:

[..]

[..]

Ik begrijp nu nog steeds niet zo goed wat precies het 'bereik' van de integraal is.
welke integraal?
quote:
Zou je kunnen zeggen dat f(n) de som is van alle f(n, k) waar k alle waarden aanneemt zodat waarvoor f(n, k) gedefinieerd is?
Dit lijkt me wel een logisch, volgens mij zijn de resultaten dan nog steeds geldig :).
de notatie is heel sloppy, en dat kun je op 2 manieren 'oplossen':
- f(n,k) = 0 stellen voor alle rare k
- de sommatie netter opschrijven en aangeven wat k mag zijn
quote:
0s.gif Op zondag 8 april 2012 18:36 schreef thenxero het volgende:

[..]

Bij lebesgue integralen zet ik ook niet de hele tijd de maat en variabele neer :) . Dan is het uit de context meestal ook wel duidelijk welke maat je gebruikt en wat je variabele is.
en bij een Riemann-Stieltjes-integraal?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
pi_110081011
quote:
0s.gif Op zondag 8 april 2012 23:37 schreef GlowMouse het volgende:
en bij een Riemann-Stieltjes-integraal?
Ik voelde hem al aankomen ;) . Dan wordt het wel vaag als je het er niet bijzet ja.
pi_110100312
quote:
0s.gif Op zondag 8 april 2012 23:37 schreef GlowMouse het volgende:

[..]

welke integraal?
Sommatie bedoel ik.
pi_110101395
quote:
14s.gif Op maandag 9 april 2012 17:12 schreef kutkloon7 het volgende:

[..]

Sommatie bedoel ik.
Lees nog eens de laatste alinea van blz. 19 van je tekst. Lijkt me toch vrij duidelijk.
Maud Wilms - Allemaol
Nadič Reyhani - The Feet Song
Yasmine - Zus
pi_110102380
quote:
0s.gif Op maandag 9 april 2012 17:40 schreef Riparius het volgende:

[..]

Lees nog eens de laatste alinea van blz. 19 van je tekst. Lijkt me toch vrij duidelijk.
True, had ik gemist.
Maar, even for the record, de recurrentievergelijking \binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k} klopt dus niet voor de randgevallen, als je bijvoorbeeld n = k = 0 gebruikt. Deels hierdoor raakte ik een beetje in de war.
pi_110102966
quote:
14s.gif Op maandag 9 april 2012 18:08 schreef kutkloon7 het volgende:

[..]

True, had ik gemist.
Maar, even for the record, de recurrentievergelijking \binom{n}{k}=\binom{n-1}{k-1}+\binom{n-1}{k} klopt dus niet voor de randgevallen, als je bijvoorbeeld n = k = 0 gebruikt. Deels hierdoor raakte ik een beetje in de war.
Een dergelijke recurrente betrekking gebruik je niet om f(n) te berekenen voor n = 0, dus ik zie je probleem niet zo.
Maud Wilms - Allemaol
Nadič Reyhani - The Feet Song
Yasmine - Zus
pi_110103451
quote:
0s.gif Op maandag 9 april 2012 18:28 schreef Riparius het volgende:

[..]

Een dergelijke recurrente betrekking gebruik je niet om f(n) te berekenen voor n = 0, dus ik zie je probleem niet zo.
Nouja, omdat je uiteindelijk die recurrente betrekking gebruikt om een formule voor de sommatie te krijgen, leek het me raar dat die recurrente betrekking niet voor alle termen in de sommatie klopt. Maar het is nu helemaal duidelijk, dank.
pi_110103709
quote:
2s.gif Op maandag 9 april 2012 18:42 schreef kutkloon7 het volgende:

[..]

Nouja, omdat je uiteindelijk die recurrente betrekking gebruikt om een formule voor de sommatie te krijgen, leek het me raar dat die recurrente betrekking niet voor alle termen in de sommatie klopt. Maar het is nu helemaal duidelijk, dank.
In het voorbeeld dat je hierboven uitwerkt leid je af dat f(n) = 2∙f(n-1), maar daar volgt niet uit dat f(0) = 1, dat haal je namelijk - impliciet - uit je definitie van f(n). Je functie f(n) is alleen gedefinieerd voor niet-negatieve gehele waarden van n en je recurrente betrekking is dus alleen geldig voor n > 0.
Maud Wilms - Allemaol
Nadič Reyhani - The Feet Song
Yasmine - Zus
pi_110120057
Kan iemand mij iets uitleggen over wiskundige economie? Zit hier al een tijd op te puzzelen, maar kom er niet uit.

Hoe kun je laten zien dat wanneer de preferentierelatie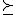 \succeq strict convex is, x* uniek is.

Ik dacht aan tx1 + (1-t)x0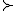 \succ x0 , dat hieruit volgt tx1 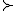\succ tx0, maar denk niet dat je zon preferentierelatie als vergelijking mag gebruiken, daarom denk ik dat dit niet goed is.
Iemand die op deze vraag het juiste antwoord weet.

En wanneer de preferentierelatie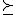 \succeq convex is, x* niet per definitie uniek is.
Hier heb ik al helemaal geen benul van :(

Iemand die hier een antwoord op weet?

Bedankt vast! :)
actieve topics nieuwe topics
abonnement Unibet Coolblue
[Bčta wiskunde] Huiswerk- en vragentopic
Index

» school, studie en onderwijs

Forum Opties
Forumhop:
Hop naar:
(afkorting, bv 'KLB')