[Bèta wiskunde] Huiswerk- en vragentopic

Sommatie van conjuctie? Ik neem aan dat je gewoon conjunctie bedoelt van alle elementen in de gegeven verzamelingen.

Volgens mij kan je dat wel zo opschrijven. Je mag vanwege associativiteit de volgorde van conjunctie veranderen, dus de tweede regel kan niet op verschillende manieren geïnterpreteerd worden.

quote:

Op zaterdag 26 november 2011 00:03 schreef thenxero het volgende:
Sommatie van conjuctie? Ik neem aan dat je gewoon conjunctie bedoelt van alle elementen in de gegeven verzamelingen.

Volgens mij kan je dat wel zo opschrijven. Je mag vanwege associativiteit de volgorde van conjunctie veranderen, dus de tweede regel kan niet op verschillende manieren geïnterpreteerd worden.

Ja weet niet hoe je dat noemt als je zeg maar 'sommeerd' over conjunctie maar gewoon conjunctie dus? "Je conjuctie over de elementen van ..." klinkt nogal raar tegenover ... Je sommeert over de elemente van ..."

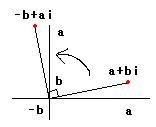
Vraag mbt complexe getallen.

Gegeven:
|1 + i| = Wortel(2)
Arg(1+i) = pi / 4.

Waarom is Arg(1 + i) = pi / 4 ???

Ik kom namelijk uit op Arg 1 + i = 1, want tan arg(1 + i) = b / a = 1 / 1 = 1

Komt het doordat de argument Theta in RADIALEN uitgedrukt wordt?? Dus tan(pi / 4) = 1....klopt dit?

Maar dan zou ik tan-1 arg(w) moeten gebruiken toch?

In het boek staat als theorie:
If w = a + bi, where a = Re(w) != 0, then tan arg(w) = tan arg(a + bi) = b / a. (Dit snap ik allemaal)

Maar ik zit nu even in de knoop met wat tangens precies is, en wanneer je tangens gebruikt, en wanneer je tan-1 (inverse van tangens) gebruikt. Ik weet overigens dat tanx = sinx / cosx.

EDIT
Tan is een verhouding tussen sin en cos. Dus bij complexe getallen, geeft tan(arg(w)) de verhouding weer tussen sin(theta) en cos(theta). Indien deze verhouding 1 is, dan betekent dat de hoek (dus arg(w)) gelijk is aan pi/4.

Klopt dit?

[ Bericht 7% gewijzigd door NonameNogame op 26-11-2011 13:44:57 ]

Tangens is overstaande zijde gedeeld door aanliggende zijde. Hier: tan(arg(w)) = 1/1, dus arg(w) = tin^-1(1)

Kijk ook eens naar http://en.wikipedia.org/w(...)ustration_modarg.svg

quote:

Op zaterdag 26 november 2011 00:59 schreef Dale. het volgende:

[..]

Ja weet niet hoe je dat noemt als je zeg maar 'sommeerd' over conjunctie maar gewoon conjunctie dus? "Je conjuctie over de elementen van ..." klinkt nogal raar tegenover ... Je sommeert over de elemente van ..."

Dat heeft er waarschijnlijk mee te maken dat je dat laatste veel vaker hebt gehoord dan dat eerste.

Zou iemand me uitkunnen leggen hoe ik de formule

quote:

K*L^-3/2

anders kan schrijven? Is dat dan?

quote:

K / (0.5*(sqrtL))

Of slaat dat nergens op?

Bedankt voor jullie hulp alvast.

quote:

Op zaterdag 26 november 2011 14:23 schreef Snuf. het volgende:
Zou iemand me uitkunnen leggen hoe ik de formule

[..]

anders kan schrijven? Is dat dan?

[..]

Of slaat dat nergens op?

Bedankt voor jullie hulp alvast.

Je zou 'm zo kunnen schrijven:

Of

quote:

Op zaterdag 26 november 2011 16:19 schreef GlowMouse het volgende:
Of

quote:

Op zaterdag 26 november 2011 14:31 schreef M.rak het volgende:

[..]

Je zou 'm zo kunnen schrijven:

Dankjulliewel, was even een beetje uit de wiskunde dus zag dit niet gelijk

quote:

Op zaterdag 26 november 2011 13:39 schreef NonameNogame het volgende:
Vraag mbt complexe getallen.

Gegeven:
|1 + i| = Wortel(2)
Arg(1+i) = pi / 4.

Waarom is Arg(1 + i) = pi / 4 ???

Kijk eens even hier en dan vooral dit plaatje. Voor a > 0 geldt Arg(a+bi) = arctan(b/a). Gebruik liever niet de (vooral Amerikaanse) notatie tan^-1x voor arctan x.

Edit: ik zie net dat je boek beweert dat dit ook zou gelden voor a < 0. Maar dat klopt niet. Om te beginnen is arg(z) voor een complex getal z (ongelijk aan nul) slechts bepaald tot op een geheel veelvoud van 2π. Je kunt dus niet zeggen dat arg(1+i) gelijk is aan ¼π. Wat wél correct is, is dat arg(1+i) = ¼π + 2kπ, k ∈ Z.

Vooral in angelsaksische literatuur wordt vaak onderscheid gemaakt tussen arg(z) en Arg(z), waarbij met het laatste de zogeheten 'hoofdwaarde' van het argument van z wordt aangegeven. Hiermee wordt doorgaans de unieke waarde van arg(z) op het interval (-π, π] bedoeld. En zo kunnen we dus inderdaad zeggen dat Arg(1+i) = ¼π. Maar omdat arctan(b/a) voor a,b ∈ R (a ≠ 0) alleen waarden op het interval (-½π, ½π) aanneemt, kan Arg(a+bi) dus alleen gelijk zijn aan arctan (b/a) voor a > 0.

[ Bericht 16% gewijzigd door Riparius op 27-11-2011 20:02:38 ]

Als A,B,C onafhankelijk exponentieel verdeeld zijn met parameters 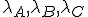, wat is dan P(A<B<C) ?

Ik heb bedacht dat

P(A<B<C) = P(A<B<C | A=min{A,B,C}) P(A=min{A,B,C}) = P(B<C | A=min{A,B,C}) P(A=min{A,B,C}),

maar weet niet hoe ik verder kan.

P(A<B<C) = P({A < max{B,C}} en {B<C}) =P(A<max{B,C})P(B<C)

De verdeling van max{B,C} kun je zo bepalen, en dan zijn die kansen makkelijk uit te rekenen.

P(max{B,C} < x ) = P(B<x, C<x) = P(B<x) P(C<x)

Dus max{B,C} is Exp(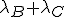) verdeeld.

edit: Thanks ik ben eruit

[ Bericht 18% gewijzigd door thenxero op 28-11-2011 16:23:12 ]

klopt dat?

quote:

Op maandag 28 november 2011 17:43 schreef GlowMouse het volgende:

klopt dat?

Ja precies. Ik had het ook nog op mijn eigen manier uitgerekend en gebruikt dat {B<C} onafhankelijk is van {A=min{A,B,C}} en daar kwam hetzelfde uit.

Ik probeer te bewijzen dat als:
(domein D in R, en punt c in D, en f:D -> R continu in c)
Als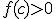 dan bestaat er een 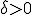zo dat voor alle 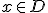met 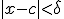geldt dat .

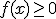Ik heb geprobeerd te werken met de definitie van continuiteit en dan f(c) als epsilon maar hiermee liep ik vast. Weet iemand of dit toch goed gaat of misschien een andere manier?

Je probeersel zou goed moeten gaan

Uit continuiteit volgt |f(x) - f(c)| < f(c) met f(c) > 0.
Als f(x) groter gelijk f(c) dan dus ook f(x) > 0.
Als f(x) < f(c) dan moet gelden:
f(c) - f(x) < f(c) dus f(x) > 0.

Dus f(x) groter gelijk 0.

Is dit correct of mis ik iets?

Je zegt nu niet hoe je aan x komt.

Uit continuiteit volgt dat voor alle x in het domein geldt |f(x) - f(c)| < f(c) met f(c) > 0. *

quote:

Op maandag 28 november 2011 22:13 schreef Anoonumos het volgende:
Uit continuiteit volgt |f(x) - f(c)| < f(c) met f(c) > 0.

Nee. De continuïteit van f in c houdt in dat er ook bij ε = f(c) > 0 een δ > 0 bestaat zodanig dat:

| f(x) - f(c) | < f(c) voor | x - c | < δ

quote:

Als f(x) groter gelijk f(c) dan dus ook f(x) > 0.
Als f(x) < f(c) dan moet gelden:
f(c) - f(x) < f(c) dus f(x) > 0.

Bedenk dat | f(x) - f(c) | = f(x) - f(c) voor f(x) ≥ f(c) en | f(x) - f(c) | = f(c) - f(x) voor f(x) ≤ f(c).

quote:

Op zaterdag 26 november 2011 17:27 schreef Riparius het volgende:

[..]

Riparius, Hartelijk dank voor je uitleg en links! Ik heb echter nog een aantal vraagjes, om te controleren of ik het helemaal snap:

Ik moest Arg(z) berekenen, de modules bepalen, en z in r (= |z|) en theta herschrijven
Vraag 10)
Gegeven: z = -2 + i
Mijn uitwerking:
a = -2, b = 1
dus r = |z| = Wortel(a^2 + b^2) = Wortel(4 + 1) = Wortel(5);
En Arg(z) -----> arctan(1/-2). Antwoord gaf aan: Arg(z) = π - arctan(1/2).

Is dit omdat a < 0 en b >= 0, en er dus geldt: Arg(z) = arctan(b/a) + π ?? Zo ja, dan wordt het antwoord dat ik hiermee verkrijg Arg(z) < -π -----> en aangezien de principal argument bereik (-π, π] heeft, diende ik π hierbij op te tellen, en dus Arg(z) = π - arctan(1/2) te moeten doen? (zodat het uiteindelijke antwoord tussen het bereik (-π, π] komt te liggen, wat voldoet aan het bereik van de principal Argument)

Een 2e vraag met deze opgave: Uit het gegeven, blijkt dat a = -2. Waarom geeft het antwoord dan arctan(1 / 2) aan? (ipv arctan(1 / -2)).

Vraag 11)
Gegeven: z = -3 - 4i
Mijn uitwerking:
a = -3, b = -4
dus r = |z| = Wortel(a^2 + b^2) = Wortel(9+16) = 5
En Arg(z) -----> arctan(-4 / -3). Aangezien zowel a<0 en b<0, moet ik dus doen: Arg(z) = arctan(-4 / -3) - π

Maar arctan(-4 / -3) = 0.9272... -> Dit valt toch binnen de range (-π, π], en dus voldoet aan de range voor de principal Argument???

Het antwoord voor Arg(z) was overigens: Arg(z) = arctan(4/3) + π (waarom positieve a- en b-waarden en wordt er π BIJgeteld??? Zou je &pi niet AF moeten trekken? immers, a en b zijn beide kleiner dan 0, en in dat geval moet je &pi aftrekken, zoals aangegeven was op de wikipedia pagina)

Vraag 12)
Gegeven: z = 3 - 4i
Mijn uitwerking:
a = 3, b = -4
r = |z| = 5
En Arg(z) = arctan(-4 / 3) -----> omdat a > 0 , hoef ik hier geen π bij op te tellen.

Antwoord was: Arg(z) = - arctan(4 / 3) ......... Waarom b = positief nu? Kan dit?

Voor vraag 12, waarom b positief is en -arctan(b / a) geschreven wordt ipv arctan(-b / a), kan ik wel wat afleiden aan de hand van goniometrie en de eenheidscirkel (simpelweg zoals in vwo-stof wiskunde staat), namelijk:
sin(-x) = -sin(x).....Zoals in de afbeelding aangegeven:


Mijn vraag hierbij is....klopt mijn redenatie? Zo ja, dan snap ik waarom arctan(-4 / 3) herschreven kan worden in -arctan(4 / 3)

Vraag 12, deel 2)
De herschrijving van z in r (= |z|) en theta
Gegeven was: z = 3 -4i
Mijn uitwerking:
a = 3
b = -4
r = |z| = 5
Er geldt verder: sinθ = b / r ..... en ..... cosθ = a / r, dan b = r·sinθ en a = r·cosθ
Aangezien de algemene regel geldt: z = a + bi (in dit geval is b negatief), dus z = a + -bi, geldt:

z = r·cosθ + i·r·sinθ ---------> z = 5(cosθ - i·sinθ) (want b was negatief)

Antwoord luidt: z = 5(cosθ + i·sinθ)........... waarom??

Een vraag hierbij is o.a.: Hoe moet ik z = 3 - 4i nu zien, als z = a + bi (met b is negatief), of als z = a - bi (met b is positief) ??

------------------------------------
Mijn excuses voor de vele en lange vragen. Ik heb geen leraar 'bij de hand' en tevens is wiskunde niet mijn studie of een onderdeel ervan. Ik vind het echter behoorlijke leuk en interessant en ik doe aan zelfstudie. Nadeel is dat ik alles zelf uit moet zoeken zonder leraar. Vandaar het gebruik van dit forum.

Alvast enorm bedankt!!

[ Bericht 0% gewijzigd door NonameNogame op 29-11-2011 22:48:13 ]

quote:

Op dinsdag 29 november 2011 22:42 schreef NonameNogame het volgende:

[..]

Riparius, Hartelijk dank voor je uitleg en links! Ik heb echter nog een aantal vraagjes, om te controleren of ik het helemaal snap:

Ik moest Arg(z) berekenen, de modules bepalen, en z in r (= |z|) en theta herschrijven
Vraag 10)
Gegeven: z = -2 + i
Mijn uitwerking:
a = -2, b = 1
dus r = |z| = Wortel(a^2 + b^2) = Wortel(4 + 1) = Wortel(5);
En Arg(z) -----> arctan(1/-2). Antwoord gaf aan: Arg(z) = π - arctan(1/2).

Over het algemeen helpt het om aan poolcoördinaten te denken. Heb je een complex getal:

(1) z = x + yi,

dan is het beeldpunt van dit getal in het complexe vlak het punt met coördinaten (x;y). Maar nu kun je de cartesische (rechthoekige) coördinaten van een punt ook omzetten naar poolcoördinaten. Heb je een punt P(x;y) dan moet je naar twee dingen kijken voor deze omzetting, namelijk de afstand OP = r (met de r van radius 'straal'), en de hoek die OP maakt met de positieve x-as. Stel dat we de positieve x-as over een hoek θ (uitgedrukt in radialen) moeten roteren om de (halve) lijn vanuit de oorsprong door punt P te krijgen, dan geldt voor de coördinaten van punt P(x;y):

(2) x = r∙cos θ
(3) y = r∙sin θ

En daar P(x;y) het beeldpunt is van ons complexe getal z = x + yi hebben we dus:

(4) z = r∙cosθ + i∙r∙sin θ = r(cos θ + i∙sin θ)

De poolcoördinaten van het beeldpunt P van z zijn dus (r;θ). Merk op dat we hier gewoonlijk i∙sin θ schrijven omdat sin θ∙i gemakkelijk aanleiding zou kunnen geven tot verwarring. Je kunt eenvoudig nagaan waarom (2) en (3) en dus ook (4) gelden, als je nog even terugdenkt aan de definitie van de sinus- en cosinusfunctie aan de hand van de eenheidscirkel. Noem je het snijpunt van lijnstuk OP of het verlengde daarvan met de eenheidscirkel P', dan zijn de coördinaten van dit punt P' per definitie (cos θ ; sin θ) omdat de cosinus en de sinus van θ gedefinieerd zijn als de x- resp. de y-coördinaat van het beeldpunt van (1;0) bij rotatie om de oorsprong over een hoek θ. En aangezien punt P het beeldpunt is van punt P' bij een meetkundige vermenigvuldiging ten opzichte van O met een factor r is het direct duidelijk dat de coördinaten van punt P dus inderdaad (r∙cos θ ; r∙sin θ) zijn.

Nu noemen we de afstand tot de oorsprong van het beeldpunt P(x;y) van het complexe getal z = x + yi de modulus (of: absolute waarde) van z, en geven we deze aan met abs(z) of |z|. Op grond van de stelling van Pythagoras is meteen duidelijk dat we hebben:

(5) |z| = √(x² + y²)

De rotatiehoek θ heet het argument van z, en deze wordt aangegeven met arg(z). Maar nu is het zo dat we na een (extra) rotatie om de oorsprong over 2π radialen, hetzij met de wijzers van de klok mee (negatief) hetzij tegen de wijzers van de klok in (positief), weer op precies hetzelfde punt uitkomen. Daarom is arg(z) niet eenduidig bepaald, maar slechts tot op een geheel veelvoud van 2π.

Nu is het in de praktijk vaak nuttig om toch over 'het' argument van een complex getal te kunnen spreken, daarom heeft men bedacht dat je de rotatie van de positieve x-as (reële as) kunt beperken tot een halve slag linksom (positief, tegen de wijzers van de klok in),of een halve slag rechtsom (negatief, met de wijzers van de klok mee). Zo kunnen we het argument altijd uitdrukken als een hoek die ligt tussen -π en +π radialen.

Alleen: wat moeten we dan doen met punten op de negatieve reële as? Want voor de getallen waarvan het beeldpunt op de negatieve reële as ligt zou je dan nog steeds net zo goed kunnen zeggen dat het argument -π is als π. De conventie is dat we dan voor de getallen op de negatieve reële as de positieve waarde π nemen. Alles samengevat ligt de 'hoofdwaarde' van het argument dan altijd op het interval (-π,π]. Deze 'hoofdwaarde' van het argument van z wordt vooral in Amerikaanse boeken aangeduid als Arg(z), dus met een hoofdletter.

Je kunt de negatieve reële as nu een beetje vergelijken met de datumgrens op aarde: als je naar het westen reist, dan kom je gaandeweg in tijdzones waar het steeds een uur vroeger is, en als je naar het oosten reist dan kom je gaandeweg in tijdzones waar het steeds een uur later is. Maar omdat de aarde rond is, kom je dan als je naar het oosten reist uiteindelijk op een punt waar je ineens overgaat van GMT+12 uur naar GMT-12 uur. Je maakt dan een sprong van precies één dag terug in de tijd en als je dan verder blijft reizen in oostelijke richting blijf je steeds in tijdzones terecht komen waar het een uur later is. Zoiets hebben we nu ook met de 'hoofdwaarde' van het augment in het complexe vlak. Als we starten in het punt (1;0), dus het beeldpunt van het (reële) getal 1, en we roteren dit punt tegen de klok in, dan neemt het argument toe tot π en we op de negatieve reële as zitten. Maar zodra we verder roteren en de negatieve reële as zijn gepasseerd hebben we een sprong gemaakt waarbij het argument met 2π is verminderd. Draaien we dan verder tegen de wijzers van de klok in, dan blijft het argument toenemen vanaf -π tot we weer op het uitgangspunt (1;0) terug zijn, en dan is het (hoofd)argument weer 0.

Nu dan je vraag. Je wil Arg(-2 + i) berekenen, dus de 'hoofdwaarde' van het argument van -2 + i. Het eerste wat je dan altijd even moet doen (in gedachten) is de ligging van het beeldpunt van dit getal in het complexe vlak visualiseren. In dit geval gaat het om het punt met de coördinaten (-2;1), en dat punt ligt in het tweede kwadrant (meestal worden de kwadranten aangegeven met Romeinse cijfers, dus kwadrant II). Dan zie je meteen dat (a) Arg(-2 + i) positief moet zijn, want (-2;1) ligt in de bovenste helft van het vlak en (b) dat de waarde in ieder geval moet liggen tussen ½π en π. Pas als je dit bedacht hebt moet je gaan rekenen.

Laten we het punt (-2;1) waar het hier om gaat weer even P noemen. Maak je nu een schetsje, dan zie je dat lijnstuk OP een hoek θ maakt met de negatieve reële as (x-as) zodanig dat

(6) tan θ = 1 : 2 = ½

en dus is:

(7) θ = arctan(½)

Maar ja, we moeten niet de hoek van lijnstuk OP met de negatieve reële as hebben, maar de hoek met de positieve reële as, en die hoek is supplementair met hoek θ. Twee hoeken noemen we supplementair als ze samen een gestrekte hoek vormen, dus een hoek van 180 graden oftewel π radialen. Voor de gezochte hoek, en daarmee voor het 'hoofdargument' van het complexe getal -2 + i vinden we dus:

(8) Arg(-2 + i) = π - arctan(½)

Maar goed, waarom werkt het niet als we gewoon arctan(1/-2) nemen zoals jij deed? Nu, dat heeft te maken met het bereik van de arctan functie. De arctan functie is de inverse functie van de tangens functie, en die geeft de hoek aan (in radialen) waarvan de tangens gelijk is aan de gegeven waarde (hier -½). De aanduiding arctan is een afkorting van arcus tangens (met arcus 'boog' omdat een hoekmaat in radialen ook als een cirkelboog op de eenheidscirkel is op te vatten). Maar nu is de tangens evenals de sinus en de cosinus een periodieke functie en wel een periodieke functie met een periode π (dit in tegenstelling tot de sinus en cosinus die elk een periode 2π hebben). Omdat de tangens een periodieke functie is kunnen we dus ook niet spreken over 'de' hoek (of: rotatie) waarvan de tangens bijvoorbeeld -½ is, want er zijn oneindig veel hoeken (rotaties) waarbij de tangens -½ is, en deze hoeken (rotaties) verschillen allemaal een geheel veelvoud van π met elkaar. En dus moest men een keuze maken.

Nu is het zo dat de tangens van een hoek θ precies éénmaal alle waarden op R aanneemt als we θ het open interval (-½π, ½π) laten doorlopen, en dus kunnen we dit ook omkeren en zo bij elke x uit R precies één waarde θ op het interval (-½π, ½π) aanwijzen waarvoor geldt dat tan θ = x. We zeggen dan dat arctan x = θ. Met arctan x wordt dus bedoeld de hoek (in radialen) op het interval (-½π, ½π) waarvan de tangens gelijk is aan x. Zo is trouwens ook de notatie te verklaren: vroeger schreef men arc. tan. x (met puntjes, als afkorting) en bedoelde men hiermee 'de boog (arcus) waarvan de tangens x is'.

Maar goed, de arctan functie neemt dus op R alleen waarden aan op het interval (-½π, ½π) en dat verklaart waarom Arg(a + bi) niet gelijk kan zijn aan arctan(b/a) voor a < 0.

quote:

Is dit omdat a < 0 en b >= 0, en er dus geldt: Arg(z) = arctan(b/a) + π ?? Zo ja, dan wordt het antwoord dat ik hiermee verkrijg Arg(z) < -π -----> en aangezien de principal argument bereik (-π, π] heeft, diende ik π hierbij op te tellen, en dus Arg(z) = π - arctan(1/2) te moeten doen? (zodat het uiteindelijke antwoord tussen het bereik (-π, π] komt te liggen, wat voldoet aan het bereik van de principal Argument)

Zo kun je het beredeneren, maar het is om vergissingen te voorkomen beter om het altijd eerst even te visualiseren.

quote:

Een 2e vraag met deze opgave: Uit het gegeven, blijkt dat a = -2. Waarom geeft het antwoord dan arctan(1 / 2) aan? (ipv arctan(1 / -2)).

Dat is hopelijk duidelijk uit het bovenstaande. Ze zijn (impliciet) uitgegaan van de supplementaire hoek. Je zou het antwoord ook kunnen schrijven als π + arctan(1/-2) aangezien arctan(-x) = -arctan(x).

quote:

Vraag 11)
Gegeven: z = -3 - 4i
Mijn uitwerking:
a = -3, b = -4
dus r = |z| = Wortel(a^2 + b^2) = Wortel(9+16) = 5
En Arg(z) -----> arctan(-4 / -3). Aangezien zowel a<0 en b<0, moet ik dus doen: Arg(z) = arctan(-4 / -3) - π

Maar arctan(-4 / -3) = 0.9272... -> Dit valt toch binnen de range (-π, π], en dus voldoet aan de range voor de principal Argument???

Het antwoord voor Arg(z) was overigens: Arg(z) = arctan(4/3) + π (waarom positieve a- en b-waarden en wordt er π BIJgeteld??? Zou je &pi niet AF moeten trekken? immers, a en b zijn beide kleiner dan 0, en in dat geval moet je &pi aftrekken, zoals aangegeven was op de wikipedia pagina)

Grote verwarring. Zowel je eigen antwoord als het antwoord dat het boek geeft (als je dat juist hebt overgenomen) zijn niet correct. Wikipedia doet het wel goed. Het beeldpunt (-3;-4) van -3 - 4i ligt in kwadrant III, dus we kunnen meteen zeggen dat de hoofdwaarde van het argument moet liggen tussen -π en -½π, en dat zie ik niet in je antwoorden.

quote:

Vraag 12)
Gegeven: z = 3 - 4i
Mijn uitwerking:
a = 3, b = -4
r = |z| = 5
En Arg(z) = arctan(-4 / 3) -----> omdat a > 0 , hoef ik hier geen π bij op te tellen.

Antwoord was: Arg(z) = - arctan(4 / 3) ......... Waarom b = positief nu? Kan dit?

Dit antwoord is wel juist. Je maakt hier gebruik van arctan (-x) = -arctan x.

quote:

Voor vraag 12, waarom b positief is en -arctan(b / a) geschreven wordt ipv arctan(-b / a), kan ik wel wat afleiden aan de hand van goniometrie en de eenheidscirkel (simpelweg zoals in vwo-stof wiskunde staat), namelijk:
sin(-x) = -sin(x).....Zoals in de afbeelding aangegeven:
[ afbeelding ]

Mijn vraag hierbij is....klopt mijn redenatie? Zo ja, dan snap ik waarom arctan(-4 / 3) herschreven kan worden in -arctan(4 / 3)

Je moet uitgaan van de tangensfunctie. Neem aan dat -½π < θ < ½π en stel tan θ = x. Dan is dus per definitie arctan x = θ. Maar omdat tan(-θ) = -tan θ en tan θ = x is dus tan(-θ) = -x en dus weer per definitie arctan(-x) = -θ. En dus geldt inderdaad arctan(-x) = -arctan x.

quote:

Vraag 12, deel 2)
De herschrijving van z in r (= |z|) en theta
Gegeven was: z = 3 -4i
Mijn uitwerking:
a = 3
b = -4
r = |z| = 5
Er geldt verder: sinθ = b / r ..... en ..... cosθ = a / r, dan b = r·sinθ en a = r·cosθ
Aangezien de algemene regel geldt: z = a + bi (in dit geval is b negatief), dus z = a + -bi, geldt:

z = r·cosθ + i·r·sinθ ---------> z = 5(cosθ - i·sinθ) (want b was negatief)

Antwoord luidt: z = 5(cosθ + i·sinθ)........... waarom??

Je introduceert hier zelf een minteken omdat je kennelijk uit wil gaan van een positieve hoek. Maar dat moet je (hier) niet doen, je kunt beter denken in termen van rotaties die zowel positief als negatief kunnen zijn. En dan heb je uitgaande van de positieve reële as aan een rotatie over een negatieve hoek tussen 0 en -½π voldoende om uit te komen op een punt in het vierde kwadrant. Formule (4) geldt altijd, ook voor negatieve rotaties, omdat immers de sinus en cosinusfuncties ook zo zijn gedefinieerd aan de hand van de eenheidscirkel.

quote:

Een vraag hierbij is o.a.: Hoe moet ik z = 3 - 4i nu zien, als z = a + bi (met b is negatief), of als z = a - bi (met b is positief) ??

Dat is inderdaad de kern. Vroeger, in de 16e en ook in de 17e eeuw, toen men pas leerde 'rekenen met letters' had men grote moeite met het idee om een uitdrukking van de gedaante z = 3 - 4i te 'zien' als z = a + bi met a = 3 en b = -4, en nam men vaak aan dat de letters positieve grootheden voorstelden. En dus 'zag' men z = 3 - 4i als z = a - bi met a = 3 en b = 4. Dat kan, maar je moet het (hier) toch niet doen omdat je dan heel gauw in verwarring raakt met bijvoorbeeld het uitrekenen van het hoofdargument. We hebben hier Arg(3 - 4i) = arctan(-4/3) = -arctan(4/3).

Voor het uitrekenen van het hoofdargument van z = x + yi bestaat een formule die ook werkt als het beeldpunt op de imaginaire as of in de linkerhelft van het complexe vlak ligt (dus voor x ≤ 0), maar om dat te begrijpen moet je wel iets weten van goniometrie.

We hebben gezien dat arctan alleen waarden aanneemt op het interval (-½π, ½π) maar dat het 'hoofdargument' ligt op het interval (-π, π], en dat is nu precies het probleem. Als we nu de (mogelijke) waarde π voor het 'hoofdargument' (getallen op de negatieve reële as) even buiten beschouwing laten, dan is het interval (-π, π) dus precies tweemaal zo breed als het interval (-½π, ½π) waarin arctan ligt, en daar kunnen we wat mee doen. Laten we zeggen dat de gezochte hoofdwaarde Arg(z) van z = x + yi (y ≠ 0 voor x ≤ 0) gelijk is aan θ. Dan is dus -π < θ < π, en dus -½π < ½θ < ½π. Maar dit betekent dat:

(9) ½θ = arctan(tan ½θ) (-π < θ < π)

en dus:

(10) Arg(x + yi) = θ = 2∙arctan(tan ½θ) (-π < θ < π)

Als we nu tan ½θ uit kunnen drukken in cos θ = x/r en sin θ = y/r, dan hebben we dus Arg(x + yi) = θ. Hiervoor gaan we uit van de bekende formules voor de sinus en cosinus van de dubbele hoek:

(11a) sin 2α = 2∙sinα∙cos α
(11b) cos 2α = 2∙cos²α - 1

Uit (11b) krijgen we

(11c) 1 + cos 2α = 2∙cos²α

Deling van de leden van (11a) door de leden van (11c) geeft dan:

(11d) sin 2α /(1 + cos 2α) = tan α,

en door substitutie van α = ½θ en dus 2α = θ krijgen we dan:

(12) tan ½θ = sin θ /(1 + cos θ)

Substitutie van (12) in (10) geeft nu:

(13) Arg(x+ yi) = 2∙arctan(sin θ /(1 + cos θ))

en aangezien cos θ = x/r en sin θ = y/r levert substitutie hiervan in (13) na wat vereenvoudiging (vermenigvuldiging van de teller en noemer van het quotiënt met r):

(14) Arg(x + yi) = 2∙arctan(y/(r + x)) (y ≠ 0 voor x ≤ 0, r = √(x² + y²))

Met deze formule kan ik bijvoorbeeld direct zeggen dat het 'hoofdargument' van -3 - 4i gelijk is aan 2∙arctan(-2), hetgeen overigens weer gelijk is aan arctan(4/3) - π zoals je gemakkelijk kunt controleren.

Er zijn nog andere manieren om (de hoofdwaarde van) het argument uit te rekenen die vooral toepasbaar zijn als je over een geschikt programma beschikt of bijvoorbeeld van WolframAlpha gebruik kunt maken. Je weet (hopelijk) dat bij vermenigvuldiging van twee complexe getallen de modulus van het product gelijk is aan het product van de moduli van de factoren en dat het argument gelijk is aan de som van de argumenten van de factoren modulo 2π. Vermenigvuldiging van een complex getal met cos θ + i∙sin θ is meetkundig te interpreteren als een rotatie van het beeldpunt van dat complexe getal om de oorsprong over een hoek θ. Je kunt dit vrij gemakkelijk inzien als je eerst beredeneert dat vermenigvuldiging van een complex getal met i meetkundig is te interpreteren als een rotatie over een rechte hoek oftewel ½π radialen in positieve zin (i.e. tegen de klok in). We hebben i(a + bi) = ai + bi² = -b + ai. Als je nu de ligging van het beeldpunt (-b;a) van -b + ai ten opzichte van het originele beeldpunt (a;b) van a + bi bekijkt dan zie gemakkelijk (congruente driehoeken) dat vermenigvuldiging met i inderdaad een rotatie in positieve zin over een rechte hoek oftewel ½π rad representeert:



Heb je dit eenmaal gezien, dan is het niet moeilijk om te begrijpen (maak een tekening!) wat er gebeurt als je een complex getal a + bi vermenigvuldigt met cos θ + i∙sinθ. We kunnen het product opsplitsen in twee delen:

(15) (cos θ + i∙sinθ)(a + bi) = cos θ∙(a + bi) + (i∙sinθ)∙(a + bi) = cos θ∙(a + bi) + i∙(sinθ∙(a + bi))

De vermenigvuldiging van een complex getal a + bi met een reëel getal zoals (hier) cos θ of sin θ is niet zo spannend: dit komt overeen met een meetkundige vermenigvuldiging van het beeldpunt met die reële factor (of, zo je wil, de vermenigvuldiging van een vector met een scalar). Het beeldpunt van de vermenigvuldiging van een complex getal a + bi met een reëel getal ligt dus op dezelfde lijn door de oorsprong als het beeldpunt (a;b) van a + bi. Maar nu hebben we voor het product van a + bi met cos θ + i∙sinθ in het rechterlid van (15) twee componenten, waarvan de tweede component sinθ∙(a + bi) ook nog eens wordt vermenigvuldigd met i. En we hebben net gezien dat vermenigvuldiging met i meetkundig een rotatie tegen de klok in over een rechte hoek representeert. Als we nu lijnstukken tekenen vanuit de oorsprong naar de beeldpunten van elk van de beide complexe getallen cos θ∙(a + bi) en i∙(sinθ∙(a + bi)) in het rechterlid van (15) dan staan die lijnstukken dus loodrecht op elkaar. En dat betekent dat we de afstand van het beeldpunt van de som en daarmee de afstand (de modulus) van het gehele product in (15) eenvoudig kunnen berekenen met de stelling van Pythagoras. Aangezien cos²θ + sin²θ = 1 vinden we voor die afstand dan √(a² + b²) zodat het beeldpunt van het product dus op dezelfde afstand van de oorsprong ligt als het beeldpunt (a;b) van a + bi zelf. Aan de modulus verandert dus niets door de vermenigvuldiging met cos θ + i∙sin θ zodat het beeldpunt van het product alleen is geroteerd ten opzichte van het beeldpunt (a;b) van a + bi. En aangezien het beeldpunt van de component cos θ∙(a + bi) langs dezelfde lijn ligt als het lijnstuk van de oorsprong naar het punt (a;b) en het beeldpunt van de component i∙(sinθ∙(a + bi)) = sinθ∙(-b + ai) op de lijn door de oorsprong loodrecht daarop, is direct in te zien dat vermenigvuldiging van een complex getal a + bi met cos θ + i∙sin θ correspondeert met een rotatie om de oorsprong van het beeldpunt (a;b) over een hoek θ.

Als je dit eenmaal inziet (en dit is fundamenteel) dan kun je hier aardige dingen mee doen. Als we het getal 1 = 1 + 0i vermenigvuldigen met cos α + i∙sin α dan is de uitkomst uiteraard cos α + i∙sin α en kunnen we zeggen dat het beeldpunt (1;0) van het getal 1 door deze vermenigvuldiging wordt geroteerd over een hoek α zodat het beeldpunt van het product uiteraard (cos α ; sin α) is. Dat is niet zo interessant, maar als we het getal cos α + i∙sin α nu weer met cos β + i∙sin β vermenigvuldigen, dan wordt het beeldpunt (cos α ; sin α) nog eens geroteerd over een hoek β. Maar dan is het beeldpunt (1;0) van het getal 1 dus uiteindelijk geroteerd over een hoek α + β, zodat we kunnen zeggen dat vermenigvuldiging met (cos α + i∙sin α)(cos β + i∙sin β) precies hetzelfde bewerkstelligt als een vermenigvuldiging met cos(α+β) + i∙sin(α+β). Zo komen we tot de conclusie dat geldt:

(16) cos(α+β) + i∙sin(α+β) = (cos α + i∙sin α)(cos β + i∙sin β)

Als je nu de haakjes in het rechterlid van (16) uitwerkt en de rekenregel i² = -1 gebruikt, dan kun je dit schrijven als:

(17) cos(α+β) + i∙sin(α+β) = (cos α∙cos β - sin α∙sin β) + i∙(sin α∙cosβ + cos α∙sin β)

Maar nu zijn twee complexe getallen uitsluitend aan elkaar gelijk als zowel de reële delen als de imaginaire delen aan elkaar gelijk zijn, en dus volgt uit (17) dat:

(18a) cos(α+β) = cos α∙cos β - sin α∙sin β
(18b) sin(α+β) = sin α∙cosβ + cos α∙sin β

Dit zijn de bekende additietheorema's uit de elementaire goniometrie. Er bestaat dus een nauw verband tussen deze somformules en de vermenigvuldiging van complexe getallen.

Aangezien voor een natuurlijk getal n het verheffen tot de macht n van een getal neerkomt op een n maal herhaalde vermenigvuldiging, kun je op grond van (16) ook nog concluderen dat geldt:

(19) (cos θ + i∙sin θ)ⁿ = cos nθ + i∙sin nθ

Dit resultaat staat bekend als de formule van De Moivre. Je kunt deze formule bijvoorbeeld gebruiken om eenvoudig goniometrische identiteiten af te leiden voor de sinus en cosinus van een veelvoud van een hoek. Ook kun je deze formule gebruiken om alle oplossingen te vinden van de vergelijking zⁿ = 1. Probeer dat eens uit voor bijvoorbeeld n = 5 en n = 6. Wat kun je zeggen over de beeldpunten van de complexe getallen die de oplossingen vormen van deze vergelijking?

De betrekking arg(z₁z₂) = arg(z₁) + arg(z₂) (mod 2π) die tot uitdrukking brengt dat bij vermenigvuldiging van twee complexe getallen de argumenten bij elkaar worden opgeteld (modulo 2π) doet je wellicht denken aan een soortgelijke betrekking bij logaritmen. De logaritme van het product van twee (positieve, reële) getallen is gelijk aan de som van de logaritmen van de factoren: log(ab) = log(a) + log(b). Nu zou je kunnen beginnen te vermoeden dat er wellicht een verband bestaat tussen logaritmen en het argument van complexe getallen. Welnu, dat is inderdaad het geval.

Het zou veel te ver voeren om hier een verantwoorde behandeling te geven van logaritmen van complexe getallen, maar ik zal toch proberen het verband tussen complexe logaritmen en het argument op een enigszins intuïtieve manier duidelijk te maken. Laten we eens aannemen dat het mogelijk is een zinnige betekenis toe te kennen aan een logaritme van een complex getal, waarbij ik even in het midden laat wat we ons daarbij zouden moeten voorstellen. Op grond van (16) hebben we dan:

(20) log(cos(α+β) + i∙sin(α+β)) = log((cos α + i∙sin α)(cos β + i∙sin β))

En omdat we mogen verwachten dat de logaritme van een product gelijk is aan de som van de logaritmen van de factoren zou dan ook moeten gelden:

(21) log(cos(α+β) + i∙sin(α+β)) = log(cos α + i∙sin α) + log(cos β + i∙sin β)

Nu kun je uit (21) opmaken dat de logaritme van een complex getal van de vorm cos θ + i∙sin θ kennelijk recht evenredig zou moeten zijn met θ, en dat is ook in overeenstemming met log(cos 0 + i∙sin 0) = log(1) = 0 voor θ = 0. Maar dan zou log(cos θ + i∙sin θ) dus gelijk moeten zijn aan θ maal een constante, en rijst onmiddellijk de vraag wat die constante dan is.

Laten we zeggen dat:

(22) z = cos θ + i∙sin θ en w = log(z),

zodat:

(23) w = log(cos θ + i∙sin θ)

Nu zou dus moeten gelden dat w recht evenredig is met θ, zodat er een constante c zou moeten zijn zodanig dat:

(24) w = c∙θ

Maar hoe vinden we die geheimzinnige constante c? Wel, als w = c∙θ dan moet gelden dw/dθ = c, zodat we de constante c zouden moeten kunnen vinden door de afgeleide dw/dθ te bepalen. En volgens de kettingregel hebben we dan:

(25) dw/dθ = dw/dz ∙ dz/dθ

Nu zouden we op grond van de afgeleide x^-1 van de reële functie log(x) kunnen veronderstellen (en meer is dat niet op dit moment) dat voor w = log(z) evenzo moet gelden:

(26) dw/dz = z^-1.

De bepaling van dz/dθ levert niet veel moeilijkheden op. De afgeleide van cos θ naar θ is -sin θ en de afgeleide van sin θ naar θ is cos θ. Maar nu is het je wellicht wel eens opgevallen dat je hebt:

(27a) d(cos t)/dt = cos(t + ½π) = -sin t
(27b) d(sin t)/dt = sin(t + ½π) = cos t

De verklaring hiervan is heel eenvoudig als je het even 'fysisch' bekijkt. Heb je een punt dat met een eenparige snelheid van 1 eenheid per seconde tegen de wijzers van de klok in langs de eenheidscirkel beweegt, te beginnen in het punt (1;0) op tijdstip t = 0, dan kun je de plaatsvector van dit punt schrijven als s(t) = cos(t)∙e_x + sin(t)∙e_y. De afgeleide s'(t) = v(t) = d(cos(t))/dt∙e_x + d(sin(t))/dt∙e_y is dan de snelheidsvector. Maar: we weten dat dit een vector moet zijn met lengte 1 die op ieder moment loodrecht staat op de plaatsvector, omdat de raaklijn aan een cirkel loodrecht staat op de straal naar het raakpunt. En omdat de beweging tegen de klok in gaat is v(t) een kwart slag in positieve zin gedraaid ten opzichte van s(t) en moet dus ook gelden v(t) = cos(t + ½π)∙e_x + sin(t + ½π)∙e_y, waaruit direct (27a) en (27b) volgen. Goed, zo hebben we dus:

(28) dz/dθ = cos(θ + ½π) + i∙sin(θ + ½π)

Maar nu weten we ook dat een rotatie over een hoek ½π beantwoordt aan een vermenigvuldiging met i, en dus kunnen we voor (28) schrijven:

(29) dz/dθ = i∙(cos θ + i∙sin θ) = i∙z

Uit (25), (26) en (29) volgt nu dat:

(30) dw/dθ = dw/dz ∙ dz/dθ = z^-1 ∙ i∙z = i

We zien nu dat dw/dθ inderdaad een constante is, en deze evenredigheidsconstante c = dw/dθ is niets anders dan de imaginaire eenheid i. En dus volgt uit (23) en (24) dat kennelijk zou moeten gelden:

(31) log(cos θ + i∙sin θ) = i∙θ

Deze betrekking staat bekend als de formule van Cotes (1682-1716), die deze betrekking in 1714 als eerste publiceerde (zij het dat hij dit op een heel andere wijze had gevonden). Nu is er echter een probleem met (31) dat ook Cotes zich destijds niet heeft gerealiseerd. Als we in (31) θ vervangen door θ + 2kπ (k ∈ Ζ), dan krijgen we uiteraard:

(32) log(cos(θ + 2kπ) + i∙sin(θ + 2kπ)) = i∙(θ + 2kπ)

Maar nu zijn de sinus en cosinus periodieke functies met een periode 2π. En dus is cos(θ + 2kπ) = cos θ en sin(θ + 2kπ) = sin θ, zodat (32) wordt:

(33) log(cos θ + i∙sin θ) = i∙(θ + 2kπ), k ∈ Ζ

Dit betekent dat we kennelijk aan de logaritme van een complex getal geen eenduidige betekenis toe kunnen kennen: de logaritme van een complex getal is slechts bepaald tot op een geheel veelvoud van 2πi. Intuïtief is dit ook wel duidelijk uit (22). Het beeldpunt van z = cos θ + i∙sin θ bevindt zich op de eenheidscirkel, en als we θ met 2π laten toenemen of afnemen dan hebben we een volledig rondje gemaakt en bevinden we ons dus weer op hetzelfde punt, terwijl de evenredigheid van log(z) met θ zou impliceren dat de logaritme dan met 2πi zou moeten zijn toegenomen of afgenomen. Zo horen er bij elk beeldpunt van een complex getal op de eenheidscirkel dus oneindig veel waarden van log(z) die echter wel allemaal een geheel veelvoud van 2πi van elkaar verschillen.

Nemen we nu een complex getal z = x + yi ongelijk aan nul, dan weten we dat we dit altijd kunnen schrijven in de vorm z = r(cos θ + i∙sin θ) waarbij (r;θ) de poolcoördinaten zijn die corresponderen met het punt (x;y) en waarbij abs(z) = |z| = r en arg(z) = θ + 2kπ, k ∈ Ζ. Nu hebben we verder op grond van de regel log(ab) = log(a) + log(b) ook:

(34) log(z) = log(r(cos θ + i∙sin θ)) = log(r) + log(cos θ + i∙sin θ),

en dus vinden we met behulp van (33):

(35) log(z) = log |z| + i∙arg(z),

waaruit weer volgt:

(36) arg(z) = -i∙log(z/|z|)

Hier heb je dus nog een formule voor arg(z). Merk op dat we in (35) en (36) arg(z) hebben, dus niet de 'hoofdwaarde' Arg(z). Immers, log(z) is slechts bepaald tot op een geheel veelvoud van 2πi evenals arg(z) slechts bepaald is tot op een geheel veelvoud van 2π. Net als bij arg(z) is het bij log(z) vaak wenselijk om met een eenduidige waarde van log(z) te kunnen werken. De - voor de hand liggende - oplossing is dan om als 'hoofdwaarde' van log(z) de waarde te nemen die in (35) correspondeert met de 'hoofdwaarde' Arg(z) van arg(z). Deze conventie wordt onder meer gevolgd door WolframAlpha en de calculator van Google.

Nog even een voorbeeld. We hadden al gevonden dat we Arg(-3 - 4i) kunnen uitdrukken als arctan(4/3) - π en als 2∙arctan(-2). Maar nu zien we dat we Arg(-3 - 4i) met behulp van (36) ook uit kunnen drukken als de 'hoofdwaarde' van -i∙log((-3 - 4i)/5). Zo hebben we drie uitdrukkingen voor Arg(-3 -4i) die er op het eerste gezicht totaal verschillend uitzien, maar die toch echt hetzelfde resultaat opleveren, zoals je in WolframAlpha kunt controleren (link: 1, 2, 3). Overigens kun je in WolframAlpha ook eenvoudig arctan(-3,-4) invoeren om Arg(-3 - 4i) te berekenen (link: 4).

quote:

------------------------------------
Mijn excuses voor de vele en lange vragen. Ik heb geen leraar 'bij de hand' en tevens is wiskunde niet mijn studie of een onderdeel ervan. Ik vind het echter behoorlijke leuk en interessant en ik doe aan zelfstudie. Nadeel is dat ik alles zelf uit moet zoeken zonder leraar. Vandaar het gebruik van dit forum.

Alvast enorm bedankt!!

[ Bericht 0% gewijzigd door Riparius op 09-12-2011 12:21:23 ]

Ik heb een probleem met de volgende vraag:

"Suppose that the amplifier transfer function is given by G(s) = 1/(s+2). If the input signal to the amplifier is a sinewave with frequency of 10 Hz and with amplitude of 1, what is the amplitude of the output signal?"

De eerste stap die ik neem is:
G(s) = 1/(s+2)
G(I*omega) = 1/(I*omega+2)

En dan zit ik eigenlijk al vast. Ik weet dat de amplitude van de output abs(G(I*omega)) is. Maar hoe kan ik dit verder uitwerken?

Waar staan s, l en omega voor? Je kan vast wel op een of andere manier die frequentie daarin invullen.