[Bèta wiskunde] Huiswerk- en vragentopic

quote:

Op woensdag 9 november 2011 15:28 schreef twaalf het volgende:

[..]

Is dat nog ergens voor nodig?

Je pakt de limiet voor h naar 0 van f ' (x+h), dus f' moet continu zijn in x anders krijg je niet f'(x).

Alleen het feit dat de afgeleide bestaat, zegt toch al dat f differentieerbaar is?

quote:

Op woensdag 9 november 2011 15:38 schreef twaalf het volgende:
Alleen het feit dat de afgeleide bestaat, zegt toch al dat f differentieerbaar is?

als f' bestaat, hoeft f' niet continu te zijn (f is wel continu)

Vreemd is dat... maar Google kon inderdaad een tegenvoorbeeld geven.

quote:

Op woensdag 9 november 2011 16:14 schreef twaalf het volgende:
Vreemd is dat... maar Google kon inderdaad een tegenvoorbeeld geven.

Ja. Maar om te bewijzen wat Physics moest bewijzen heb je L'Hôpital niet nodig en dus ook niet dat f' continu is, want het gevraagde volgt ook direct uit de definitie van de afgeleide (maar inderdaad, de opdracht was om wél de regel van L'Hôpital te gebruiken).

quote:

Op woensdag 9 november 2011 19:01 schreef Riparius het volgende:

[..]

het gevraagde volgt ook direct uit de definitie van de afgeleide

Zeker niet, pak f(x) = 1 als x != 0, f(0) = 0. Dan zou je krijgen f'(0) = 0.

quote:

Op woensdag 9 november 2011 19:31 schreef GlowMouse het volgende:

[..]

Zeker niet, pak f(x) = 1 als x != 0, f(0) = 0. Dan zou je krijgen f'(0) = 0.

Maar dat probleem heb je toch ook als je het met L'Hopital wil bewijzen?

Het punt van de opgave is om te laten zien dat: als f continu differentieerbaar is, dan is die limiet equivalent met de definitie van de afgeleide. Maar jouw functie is niet differentieerbaar in x=0.

Je had ook de volgende substituties kunnen doen:
y = x + h/2
Dan krijg je



En dan k=h/2 geeft

quote:

Op woensdag 9 november 2011 19:52 schreef thenxero het volgende:

[..]

Maar dat probleem heb je toch ook als je het met L'Hopital wil bewijzen?

Klopt, maar onder de aanname dat f cont.diff.baar is, is f continu, en heb je het genoemde probleem niet meer.

Met jouw voorbeeld bereken je na substitutie niet meer de afgeleide in x. Je kunt niet zomaar dingen lopen vervangen.

Dit is misschien voor jullie simpel, maar voor mij erg moeilijk. Ik en de leraar kwamen allebei op een ander antwoord dan het programma waarin we werken, en nu vroeg ik me af op wat voor antwoord anderen komen..

Vraag: Reken uit op maximaal vijf cijfers achter de komma (het vijfde cijfer niet afronden) en rond dan af op twee cijfers achter de komma.

Som:
137:15 =

Volgens het programma moet dit het antwoord zijn: 9,13333 en afgerond op twee cijfers is dat 9,13. Kan iemand mij vertellen of het programma het misschien fout heeft? Zelfs de leraar kwam op een ander antwoord uit. En mocht het programma het wel goed hebben, iemand die mij een goede methode kan delen voor dit soort sommen?

quote:

Op woensdag 9 november 2011 20:22 schreef Maincoon het volgende:
Dit is misschien voor jullie simpel, maar voor mij erg moeilijk. Ik en de leraar kwamen allebei op een ander antwoord dan het programma waarin we werken, en nu vroeg ik me af op wat voor antwoord anderen komen..

Vraag: Reken uit op maximaal vijf cijfers achter de komma (het vijfde cijfer niet afronden) en rond dan af op twee cijfers achter de komma.

Som:
137:15 =

Volgens het programma moet dit het antwoord zijn: 9,13333 en afgerond op twee cijfers is dat 9,13. Kan iemand mij vertellen of het programma het misschien fout heeft? Zelfs de leraar kwam op een ander antwoord uit. En mocht het programma het wel goed hebben, iemand die mij een goede methode kan delen voor dit soort sommen?

Intypen op google geeft: 137 / 15 = 9,13333333. Als je het met de hand wil doen: staartdeling.

9,13 is juist. Hoe kom je ergens anders op uit?

quote:

Op woensdag 9 november 2011 20:19 schreef GlowMouse het volgende:

[..]

Klopt, maar onder de aanname dat f cont.diff.baar is, is f continu, en heb je het genoemde probleem niet meer.

Met jouw voorbeeld bereken je na substitutie niet meer de afgeleide in x. Je kunt niet zomaar dingen lopen vervangen.

Jawel, wat thenxzero doet klopt onder de voorwaarde dat f differentieerbaar is. Hier wordt nergens gebruikt dat de afgeleide functie f' zelf ook continu zou moeten zijn.

Je zou ook kunnen zeggen dat je

(1) (f(x+h) - f(x-h))/2h

Kunt herschrijven als:

(2) ½∙(f(x+h) - f(x))/h + ½∙(f(x-h) - f(x))/(-h)

Als nu f differentieerbaar is dan bestaat de limiet voor h → 0 van elk van beide termen in (2) en zijn deze limieten elk gelijk aan ½∙f'(x). Maar daaruit volgt dat de limiet voor h → 0 van de som (1) ook bestaat en gelijk is aan f'(x).

Ja klopt, maar je hebt wel een aanname nodig.

quote:

Op woensdag 9 november 2011 21:39 schreef GlowMouse het volgende:
Ja klopt, maar je hebt wel een aanname nodig.

Ja, dat f differentieerbaar is, niet dat de afgeleide f' continu is, terwijl die tweede aanname wel nodig is als je hier met L'Hôpital wil werken. Ik begrijp je kritiek op mijn opmerking hierboven dan ook niet, en thenxzero kennelijk ook niet. Je lijkt te denken dat het bestaan van de limiet van uitdrukking (1) voor h → 0 impliceert dat de limieten voor elk van de beide uitdrukkingen in (2) voor h → 0 ook moeten bestaan, en dat dus ook de afgeleide f'(x) moet bestaan, maar dat is niet zo. Het omgekeerde geldt echter wel. Als de afgeleide f'(x) bestaat, dan bestaan de limieten voor h → 0 van elk van beide termen in (2) en daarmee ook de limiet voor h → 0 van de som (1).

quote:

Op woensdag 9 november 2011 21:56 schreef Riparius het volgende:

[..]

Je lijkt te denken dat het bestaan van de limiet van uitdrukking (1) voor h → 0 impliceert dat de limieten voor elk van de beide uitdrukkingen in (2) voor h → 0 ook moeten bestaan, en dat dus ook de afgeleide f'(x) moet bestaan

Dan moet je er niet zonder meer een gelijkheidsteken tussenzetten. Zonder de onvermelde aanname van differentieerbaarheid zou de linkerkant wel, en de rechterkan niet gedefinieerd zijn.

quote:

Op woensdag 9 november 2011 22:01 schreef GlowMouse het volgende:

[..]

Dan moet je er niet zonder meer een gelijkheidsteken tussenzetten. Zonder de onvermelde aanname van differentieerbaarheid zou de linkerkant wel, en de rechterkan niet gedefinieerd zijn.

Nee, dat is niet het probleem. Ik herschijf het quotiënt, niet de limiet van dat quotiënt. De uitdrukkingen (1) en (2) zijn aan elkaar gelijk als de functiewaarden zijn gedefinieerd en h ongelijk is aan 0 (want voor h = 0 zijn de uitdrukkingen ongedefinieerd). Ik zeg niet dat de limiet van een uitdrukking die je als een som van twee termen kunt schrijven gelijk is aan de som van de limieten van die twee termen, want dat hoeft nu juist niet zo te zijn (terwijl het omgekeerde wel geldt).

Het ging hierom:
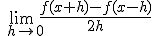=f'(x)

daarover zeg jij:

quote:

Op woensdag 9 november 2011 19:01 schreef Riparius het volgende:

[..]

Ja. Maar om te bewijzen wat Physics moest bewijzen [wat hierboven staat dus] heb je L'Hôpital niet nodig en dus ook niet dat f' continu is, want het gevraagde volgt ook direct uit de definitie van de afgeleide (maar inderdaad, de opdracht was om wél de regel van L'Hôpital te gebruiken).

en dat klopt niet. En ik ben er klaar mee.

quote:

Op woensdag 9 november 2011 22:15 schreef GlowMouse het volgende:
Het ging hierom:
=f'(x)

daarover zeg jij:

[..]

en dat klopt niet. En ik ben er klaar mee.

Ik zie nog steeds niet waarom hetgeen ik beweerde niet zou kloppen. Om te beginnen laat je in het citaat van Physics nu wel de eerste regel weg en die is essentieel:

Zij f' continu, laat zien d.m.v. L'Hospital dat ...

Aangezien het betekenisloos is te spreken over de afgeleide f' (laat staan te zeggen dat f' continu is) als f' niet bestaat en aangezien hetgeen aangetoond moet worden ook geen betekenis heeft als f'(x) niet is gedefinieerd is dus wel degelijk gegeven dat de afgeleide van f bestaat. Je kunt namelijk onmogelijk de juistheid of onjuistheid bewijzen van een uitspraak die betekenisloos is. Ik doe dus geen additionele aannames. Mijn argument was alleen dat het niet nodig is te veronderstellen dat de afgeleide f' continu is als we geen gebruik maken van de regel van L'Hôpital omdat het gevraagde ook direct uit de definitie van de afgeleide volgt.

Aangezien f'(x) bestaat volgt uit definitie van de afgeleide:

(1) lim_h→0 (½∙(f(x+h) - f(x))/h) = ½∙f'(x)

En aan de hand van de ε,δ definitie van de limiet is eenvoudig aan te tonen dat dan ook geldt:

(2) lim_h→0 (½∙(f(x-h) - f(x))/(-h)) = ½∙f'(x)

En aangezien de limiet van een som gelijk is aan som van de limieten van de termen mits die bestaan volgt uit (1) en (2) dat ook geldt:

(3) lim_h→0 ((½∙(f(x+h) - f(x))/h) + (½∙(f(x-h) - f(x))/(-h))) = f'(x)

En dus:

(4) lim_h→0 ((f(x+h) - f(x-h))/2h) = f'(x)

QED

We kunnen dit echter niet omkeren: uit het bestaan van de limiet in het linkerlid van (4) volgt niet het bestaan van de limieten in het linkerlid van (1) en (2) en daarmee ook niet het bestaan van de afgeleide f'(x).

Dat is wel een net bewijsje, ja. Ik ging er ook vanuit dat f differentieerbaar was, anders is het vreemd om over f ' te spreken.

Consider [tex]A = \begin{pmatrix} 0 & 0 &0 &0 &0 &1\\
0 &0 &0 &0 &1&1\\
0 &1 &0 &0 &0 &0\\
1&1&0 &0 &0 &0\\
0 &0 &0 &1&0&0\\
0 &0 &1 & 1&0&0 \end{pmatrix} [/tex]

Is deze matrix primitief? Hij is niet primitief, maar hoe bewijs ik dat?

Wat is een primitieve matrix?

Een matrix waarvoor geldt dat A^m is postitief voor een zeker m

Verder zijn er nog theorieën dat als A irreduceerbaar is en de Trace van A > 0, A dan primitief is, maar Tr(A) is in dit geval 0.

Als je het echt niet weet kan je altijd proberen de matrix een paar keer met zichzelf te vermenigvuldigen en kijken wat er gebeurt. Misschien dat je het dan wel ziet.

Bedoel je trouwens met een positieve matrix dat ieder element positief is? Of bedoel je positief definiet.

quote:

Op donderdag 10 november 2011 19:23 schreef thenxero het volgende:
Als je het echt niet weet kan je altijd proberen de matrix een paar keer met zichzelf te vermenigvuldigen en kijken wat er gebeurt. Misschien dat je het dan wel ziet.

Dan krijg je wel een vermoeden, maar geen bewijs

quote:

Op donderdag 10 november 2011 19:24 schreef Alxander het volgende:

[..]

Dan krijg je wel een vermoeden, maar geen bewijs

Niet direct maar misschien vind je een formule voor A^m bijvoorbeeld.
Bedoel je trouwens met een positieve matrix dat ieder element positief is? Of bedoel je positief definiet.