SES School, Studie en Onderwijs
Wiskunde in de brugklas, Frans voor het examen of een studie Personeel en Arbeid? Moeilijke formulieren van DUO? Iets weten over studiefinanciering of studentenverenigingen? Dit is het forum voor leerkrachten, scholieren en studenten, van brugklas tot uni
Dat impliceert dat de ruimte second countable is en omdat die bovendien normaal is, volgt met Urysohn's metrizatie stelling dat de ruimte metrizeerbaar is en dus is de aftelbare vereniging van gesloten disjuncte deelverzamelingen weer gesloten.
?
?
In een metriseerbare ruimte is het niet noodzakelijk zo dat een aftelbare vereniging van disjuncte gesloten deelverzamelingen gesloten is.
Zit even vast met een mooie 'equation' voor het volgende:
From the set of available roles, we get the set of roles with the highest priority.
Dus je hebt een set of available roles: Available = {role1, role2, role3}
elke element in deze set heeft een priority (soort score)
en nu wil ik de set van roles die dezelfde priority hebben als de role met de hoogste priority in de Available set.
Ik zit vast met het 'nice' opschrijven van de max verkrijgen en dan de set met die waarde.
From the set of available roles, we get the set of roles with the highest priority.
Dus je hebt een set of available roles: Available = {role1, role2, role3}
elke element in deze set heeft een priority (soort score)
en nu wil ik de set van roles die dezelfde priority hebben als de role met de hoogste priority in de Available set.
Ik zit vast met het 'nice' opschrijven van de max verkrijgen en dan de set met die waarde.
Gebruikelijk is dat f(A) het beeld is van A onder f. Daarmee is het opschrijven eenvoudig:
{a in A | prio(a) = max prio(A) }
{a in A | prio(a) = max prio(A) }
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Goedemorgen allemaal!
Wie kan mij een aanwijzing geven voor het oplossen van deze vergelijking? Ik heb al meerdere dingen geprobeerd, maar het enige dat ik krijg is hoofdpijn... Ik heb de noemers proberen weg te vermenigvuldigen, maar dat leverde alleen maar een complexere vergelijking op. Ook heb ik de cos2 x veranderd naar sin, maar dat was ook niet wat ik zocht.
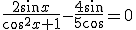
Wie kan mij een aanwijzing geven voor het oplossen van deze vergelijking? Ik heb al meerdere dingen geprobeerd, maar het enige dat ik krijg is hoofdpijn... Ik heb de noemers proberen weg te vermenigvuldigen, maar dat leverde alleen maar een complexere vergelijking op. Ook heb ik de cos2 x veranderd naar sin, maar dat was ook niet wat ik zocht.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Als cos˛x +1 != 0 en cos x != 0 dan kun je deze vergelijking herschrijven naar:
10 sinx cos x = 4 sin x (cos˛x + 1)
1 oplossing kun je nu direct aflezen. Daarna moet je deze vergelijking nog oplossen:
5 cos x = 2 cos˛x + 2
Dit is een kwadratische vergelijking in cos x. Vervang cos x door y, en je kunt hem zo oplossen.
10 sinx cos x = 4 sin x (cos˛x + 1)
1 oplossing kun je nu direct aflezen. Daarna moet je deze vergelijking nog oplossen:
5 cos x = 2 cos˛x + 2
Dit is een kwadratische vergelijking in cos x. Vervang cos x door y, en je kunt hem zo oplossen.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Oké. Ik zie dat je de noemers tegen elkaar weg hebt vermenigvuldigd. Daar had ik niet eens aan gedacht. Wat gebeurd er met de formule die daar uit voortkomt? Ik zie namelijk dat de sin x is verdwenen?quote:Op woensdag 1 juni 2011 10:45 schreef GlowMouse het volgende:
Als cos˛x +1 != 0 en cos x != 0 dan kun je deze vergelijking herschrijven naar:
10 sinx cos x = 4 sin x (cos˛x + 1)
1 oplossing kun je nu direct aflezen. Daarna moet je deze vergelijking nog oplossen:
5 cos x = 2 cos˛x + 2
Dit is een kwadratische vergelijking in cos x. Vervang cos x door y, en je kunt hem zo oplossen.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
quote:
[..]
Oké. Ik zie dat je de noemers tegen elkaar weg hebt vermenigvuldigd. Daar had ik niet eens aan gedacht.
je stelde het zelf voor: "Ik heb de noemers proberen weg te vermenigvuldigen"Niet verdwenen, ik lees een oplossing af.quote:Wat gebeurdt er met de formule die daar uit voortkomt? Ik zie namelijk dat de sin x is verdwenen?
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
quote:
[..]
Inderdaad. Maar niet tegen elkaar weg. Ik ben nog niet zo vertrouwd met dit soort dingen.Ow op dit manier. Dan kan ik me er in vinden.quote:
[..]
Niet verdwenen, ik lees een oplossing af.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Vraagje moet bn+1 dan opgeteld worden bij het negatieve getal? of bij het positieve getal voor de operatie?quote:
[..]
Dat als er een negatief getal uitkomt (wat mogelijk is, aangezien je het quotient slechts benadert in Stap D3) dat je er dan bn+1 bij op moet tellen, maar dat je dat dan wel moet onthouden.
De uitdrukking 'noemers tegen elkaar weg vermenigvuldigen' is niet gebruikelijk en ook nogal bedenkelijk. Dat is niet wat je doet. Als je hebt:quote:
[..]
Oké. Ik zie dat je de noemers tegen elkaar weg hebt vermenigvuldigd. Daar had ik niet eens aan gedacht. Wat gebeurt er met de formule die daar uit voortkomt? Ik zie namelijk dat de sin x is verdwenen?
(1) a/b = c/d
dan kan ik beide leden van deze gelijkheid met het product bd vermeningvuldigen. Uiteraard hebben a/b en c/d alleen betekenis als b resp. d niet nul zijn, want delen door nul is niet gedefinieerd. Welnu, aangezien bd∙a/b = adb/b = ad en bd∙c/d = bcd/d = bc krijgen we dan:
(2) ad = bc
De stap van (1) naar (2) wordt ook wel 'kruislings vermenigvuldigen' genoemd. Die benaming wordt vooral duidelijk als je de breuken a/b en c/d in (1) even opschrijft met horizontale breukstrepen.
In je oorspronkelijke vergelijking kun je een factor sin x buiten haakjes halen, waardoor je weer een product hebt van twee factoren dat gelijk moet zijn aan nul, zodat (tenminste) een der factoren nul moet zijn. Die factor sin x 'verdwijnt' dus niet. Bij deze goniometrische vergelijking moet je er ook op letten dat zowel cos2x + 1 als cos x niet nul mogen zijn, aangezien deze beide optreden als noemer in de oorspronkelijke vergelijking. Ik denk dat je er verstandig aan doet nog eens een remedial course in elementaire algebra te doen, anders zul je ook verderop in je studie steeds weer vastlopen op dit soort dingen.
Bij het negatieve getal.quote:Op woensdag 1 juni 2011 14:32 schreef Dale. het volgende:
[..]
Vraagje moet bn+1 dan opgeteld worden bij het negatieve getal? of bij het positieve getal voor de operatie?
In een opgave moet ik bepalen op welke punten een Lissajous-figuur een horizontale raaklijn heeft. Ik heb de afgeleide gebruikt van de Y-as, aangezien die as bepalend is of een lijn horizontaal loopt of kantelt. Nu blijkt dus dat het antwoord juist voortkomt uit de X-as. Maak ik nou een denkfout?
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Als de x-as horizontaal is en de y-as verticaal (zoals gebruikelijk), dan betekent een horizontale lijn dat de y-coördinaat constant blijft en dus de afgeleide van de y-coördinaat 0 is. Dat lijkt me goed...
De afgeleide van de x-coordinaat moet niet tegelijk 0 zijn.
eee7a201261dfdad9fdfe74277d27e68890cf0a220f41425870f2ca26e0521b0
Ik geloof niet dat ik je begrijp...?quote:
De afgeleide van de x-coordinaat moet niet tegelijk 0 zijn.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Je moet wat duidelijker uitleggen wat er gegeven is. Als je de x- en y-coördinaten van je figuur beide hebt als parametervoorstellingen van, laten we zeggen, een parameter t, dan is de voorwaarde voor een horizontale raaklijn dy/dt = 0, terwijl dx/dt daarbij niet nul mag zijn.quote:
Als de afgeleiden van beide coördinaten nul zijn dan verandert zowel de x als y-coördinaat niet, en dus krijg je een punt.quote:
Ik zal even iets specifieker zijn. Het gaat om het volgende figuur:
Waar de volgende formules bij horen: x = cos 2t en y = cos 3t. De vraag is: "Bij welke twee punten is de raaklijn aan de baan van P horizontaal?" en dit moet ik dan exact berekenen. Normaliter zou ik de afgeleide nemen en dan bepalen waar 0 zit en vervolgens vaststellen wat voor extreem dat is. Alleen dat werkt hier dus niet bij.
Waar de volgende formules bij horen: x = cos 2t en y = cos 3t. De vraag is: "Bij welke twee punten is de raaklijn aan de baan van P horizontaal?" en dit moet ik dan exact berekenen. Normaliter zou ik de afgeleide nemen en dan bepalen waar 0 zit en vervolgens vaststellen wat voor extreem dat is. Alleen dat werkt hier dus niet bij.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
De afgeleide van y is dus 0, dan is de raaklijn aan de curve namelijk horizontaal. Daaruit kan je t bepalen. Vervolgens neem je de waardes van t binnen bijvoorbeeld het interval [0, 2pi]. Invullen in formule voor de x en y coordinaat en je hebt de gevraagde punten.quote:
Ik zal even iets specifieker zijn. Het gaat om het volgende figuur:
[ afbeelding ]
Waar de volgende formules bij horen: x = cos 2t en y = cos 3t. De vraag is: "Bij welke twee punten is de raaklijn aan de baan van P horizontaal?" en dit moet ik dan exact berekenen. Normaliter zou ik de afgeleide nemen en dan bepalen waar 0 zit en vervolgens vaststellen wat voor extreem dat is. Alleen dat werkt hier dus niet bij.
[img]http://i.minus.com/ibnbBZVlYCvsZI.gif[/img]
Oké. Ik begrijp al wat ik verkeerd deed. Ik ging er vanuit dat het antwoord voortkwam uit de afgeleide van de Y-as. Maar het is natuurlijk T wat daaruit voortkomt, dus daaruit moet dan nog het volgende antwoord gehaald worden. In dit geval (-½, -1) en (-½, 1).quote:
[..]
De afgeleide van y is dus 0, dan is de raaklijn aan de curve namelijk horizontaal. Daaruit kan je t bepalen. Vervolgens neem je de waardes van t binnen bijvoorbeeld het interval [0, 2pi]. Invullen in formule voor de x en y coordinaat en je hebt de gevraagde punten.
Is het trouwens zo dat wanneer zo'n figuur een periode heeft van 2π dat je dan over dat bereik nulpunten moet bereken? Ik kwam er namelijk achter dat de periode van dit figuur 2π is, maar dat P dezelfde weg terug neemt en je dus eigenlijk 4 nulpunten hebt.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Je formuleringen zijn een beetje vaag... iets als een "afgeleide van de y-as" bestaat niet. Je neemt afgeleides van functies, niet van assen.quote:
[..]
Oké. Ik begrijp al wat ik verkeerd deed. Ik ging er vanuit dat het antwoord voortkwam uit de afgeleide van de Y-as. Maar het is natuurlijk T wat daaruit voortkomt, dus daaruit moet dan nog het volgende antwoord gehaald worden. In dit geval (-½, -1) en (-½, 1).
Is het trouwens zo dat wanneer zo'n figuur een periode heeft van 2π dat je dan over dat bereik nulpunten moet bereken? Ik kwam er namelijk achter dat de periode van dit figuur 2π is, maar dat P dezelfde weg terug neemt en je dus eigenlijk 4 nulpunten hebt.
Als je alle nulpunten wil vinden is het inderdaad voldoende om alleen te kijken in een interval met de lengte van de periode.
Inderdaad. Het is de afgeleide van de functie die de Y-as bepaalt.quote:
[..]
Je formuleringen zijn een beetje vaag... iets als een "afgeleide van de y-as" bestaat niet. Je neemt afgeleides van functies, niet van assen.
Op dinsdag 24 mei 2011 07:11 schreef Absurditeit het volgende:
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
Het werkt ook niet echt erotiserend als je de rookworst en saucijzenbroodjes op 45 meter afstand al ruikt, terwijl je langs de plastic laarzen en kledij loopt.
